Sparse Binary Representation Learning for Knowledge Tracing
Yahya Badran
1,2 a
and Christine Preisach
1,2 b
1
Karlsruhe University of Applied Sciences, Moltekstr. 30, 76133 Karlsruhe, Germany
2
Karlsruhe University of Education, Bismarckstr 10,76133 Karlsruhe, Germany
Keywords:
Knowledge Tracing, Deep Learning, Representation Learning, Knowledge Concepts.
Abstract:
Knowledge tracing (KT) models aim to predict students’ future performance based on their historical interac-
tions. Most existing KT models rely exclusively on human-defined knowledge concepts (KCs) associated with
exercises. As a result, the effectiveness of these models is highly dependent on the quality and completeness
of the predefined KCs. Human errors in labeling and the cost of covering all potential underlying KCs can
limit model performance. In this paper, we propose a KT model, Sparse Binary Representation KT (SBRKT),
that generates new KC labels, referred to as auxiliary KCs, which can augment the predefined KCs to address
the limitations of relying solely on human-defined KCs. These are learned through a binary vector represen-
tation, where each bit indicates the presence (one) or absence (zero) of an auxiliary KC. The resulting discrete
representation allows these auxiliary KCs to be utilized in training any KT model that incorporates KCs.
Unlike pre-trained dense embeddings, which are limited to models designed to accept such vectors, our dis-
crete representations are compatible with both classical models, such as Bayesian Knowledge Tracing (BKT),
and modern deep learning approaches. To generate this discrete representation, SBRKT employs a binariza-
tion method that learns a sparse representation, fully trainable via stochastic gradient descent. Additionally,
SBRKT incorporates a recurrent neural network (RNN) to capture temporal dynamics and predict future stu-
dent responses by effectively combining the auxiliary and predefined KCs. Experimental results demonstrate
that SBRKT outperforms the tested baselines on several datasets and achieves competitive performance on
others. Furthermore, incorporating the learned auxiliary KCs consistently enhances the performance of BKT
across all tested datasets.
1 INTRODUCTION
Knowledge tracing is a fundamental task in educa-
tional data mining that involves modeling a student’s
mastery of knowledge concepts (KCs) over time to
predict future performance. Accurate knowledge trac-
ing enables personalized learning experiences, adap-
tive tutoring systems, and informed instructional de-
cisions. Traditional models, such as Bayesian Knowl-
edge Tracing (BKT)(Corbett and Anderson, 1994)
and Deep Knowledge Tracing (DKT)(Piech et al.,
2015), often rely on predefined KCs associated with
each exercise. However, these predefined KCs may
not fully capture the underlying complexities and la-
tent structures of the learning process.
Recent advancements in representation learning
have introduced the possibility of uncovering latent
knowledge through data-driven methods by learning
a
https://orcid.org/0009-0006-9098-5799
b
https://orcid.org/0009-0009-1385-0585
a new representation of the data. This approach has
been utilized in different areas of machine learning in-
cluding education data mining (Bengio et al., 2013a;
Liu et al., 2020). By leveraging exercise embeddings
and neural networks, we can identify hidden patterns
and relationships that are not immediately apparent
from predefined KCs alone. These representations
can be further utilized in downstream tasks, which,
in our case, involve using the learned representations
to improve the performance of simpler models, such
as BKT.
In this paper, we propose a model that learns a rep-
resentation that can be further utilized by other KT
models. Specifically, we train a neural network to
learn sparse binary vector for each exercise. These
vectors can be used to extract further latent labels,
which we refer to as auxiliary knowledge concepts
(auxiliary KCs). In this context, a value of one in
the binary vector indicates the presence of an auxil-
iary KC, while a value of zero indicates its absence.
This can help mitigate the possible lack of coverage
Badran, Y. and Preisach, C.
Sparse Binary Representation Learning for Knowledge Tracing.
DOI: 10.5220/0013275100003932
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 2, pages 75-84
ISBN: 978-989-758-746-7; ISSN: 2184-5026
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
75

in the human pre-defined KCs. For example, human-
defined KCs may fail to distinguish between varia-
tions in exercises that involve the same concept, such
as addition with single-digit numbers versus addition
with decimals. Auxiliary KCs could capture such
distinctions, ensuring a more coverage of the latent
knowledge.
However, these auxiliary KCs do not possess ex-
plicit human labels. Instead, in this work, we use
these auxiliary KCs in downstream tasks to improve
the performance of other knowledge tracing (KT)
models. By integrating these auxiliary KCs into mod-
els like BKT that assume independence between KCs,
we aim to enhance their predictive capabilities with-
out compromising their interpretability. Future work
can investigate the possible advantages of displaying
these KCs to students, as well as the potential to as-
sign meaningful human labels to them.
Our approach involves the following steps:
1. Knowledge tracing that learns a discrete and
sparse representation: We develop a neural network
model that learns a sparse binary vector for each ex-
ercise based on student interaction data.
2. Extracting Auxiliary KCs from the binary rep-
resentation: The learned binary representation repre-
sent further latent discrete features that we call auxil-
iary KCs.
3. Integration with downstream models: We uti-
lize these auxiliary KCs in downstream knowledge
tracing models, such as BKT and DKT to enhance
their performance.
We evaluate our model on real-world educational
datasets to assess its effectiveness in improving pre-
dictive performance over traditional methods. The
results demonstrate that incorporating auxiliary KCs
learned through our proposed model generally en-
hances the accuracy of knowledge tracing models, of-
ten yielding significant improvements.
The contributions of this paper are threefold:
• We introduce a model that learns sparse binary
representations, which can be used to extract aux-
iliary KCs.
• We demonstrate how these learned representa-
tions can be utilized in other models such as BKT,
improving their predictive performance while
maintaining simplicity and interpretability.
• We perform extensive experiments on real-world
datasets to demonstrate the effectiveness of our
approach.
In the following sections, we review related work
in knowledge tracing and representation learning, de-
tail our methodology for learning and integrating aux-
iliary KCs, present experimental results, and discuss
the implications of our findings for educational data
mining.
2 RELATED WORK
Early approaches to knowledge tracing, such as
Bayesian Knowledge Tracing (BKT) (Corbett and
Anderson, 1994), utilize a Hidden Markov Model
(HMM) to model each knowledge component (KC)
independently. BKT represents student knowledge
using two binary states: mastered and not mastered,
with transitions between these states governed by in-
terpretable probabilities for slip, guess, and learning.
While this simple structure ensures high interpretabil-
ity, BKT’s strong independence assumption ignores
dependencies between KCs, limiting its expressive-
ness. Furthermore, its straightforward probability-
based framework often underperforms compared to
deep learning-based models, which excel at captur-
ing complex and intricate relationships between KCs
(Gervet et al., 2020; Khajah et al., 2016).
Deep Knowledge Tracing (DKT) (Piech et al.,
2015) introduced a neural network-based approach to
knowledge tracing by employing a recurrent neural
networks (RNNs) to model temporal knowledge state
change during coursework. DKT was followed by
numerous models that utilized different deep learn-
ing architectures such as transformers like architec-
ture (Ghosh et al., 2020) and memory based neural
networks (Zhang et al., 2017).
Dynamic Key-Value Memory Networks
(DKVMN) (Zhang et al., 2017) uses a static
key memory, a fixed matrix, which remain consistent
across interactions to capture the inherent relation-
ships between exercises and underlying concepts.
Alongside this, a dynamic value memory is main-
tained to track the evolving mastery levels of these
concepts as students engage with exercises. DKVMN
does not utilize the human predefined KCs in the
dataset, instead they consider the static key memory
to be a model of the latent concepts in the dataset.
Given that KCs are human-predefined tags and
therefore prone to errors, some studies aim to mitigate
potential inaccuracies by learning methods to correct
or calibrate these human-defined KCs (Wang et al.,
2021; Li and Wang, 2023; Wang et al., 2022). This
approach differs from our work, as we do not attempt
to modify or correct the contributions of human ex-
perts. Instead, we focus on augmenting the existing
KCs with newly derived auxiliary KCs to enhance
model performance.
Papers such as (Liu et al., 2020; Wang et al.,
2024) propose models that learn vector embeddings
CSEDU 2025 - 17th International Conference on Computer Supported Education
76

for downstream knowledge tracing tasks. However,
these embeddings are dense, making them less inter-
pretable and limiting their applicability to deep learn-
ing models. In contrast, our approach learns discrete,
sparse binary representations that map each question
to a new set of auxiliary KCs. These representations
are versatile, as they can be utilized by both deep
learning and classical models, where the latter can of-
fer greater interpretability.
In (Nakagawa et al., 2018), the authors propose
a method to learn new KCs for each question, fully
replacing the original KCs defined by experts. This
approach aligns with methods that aim to recalibrate
human-defined KCs. Each question is represented as
a binary vector, where a value of one indicates that
the corresponding dimension is a KC associated with
the question. However, their model does not directly
produce a binary representation. Instead, it relies on a
continuous representation with a regularization term
to encourage closeness to a binary vector, with bina-
rization applied only after training. In contrast, our
model explicitly learns a binary representation to de-
fine new auxiliary KCs. While our approach could be
adapted to entirely replace the original KCs, this is
not the primary objective of our research.
3 BACKGROUND
In this section, we provide an overview of knowledge
tracing models that are relevant to this work.
3.1 Bayesian Knowledge Tracing
Bayesian Knowledge Tracing (BKT)(Corbett and An-
derson, 1994) is formulated as a Hidden Markov
Model (HMM), where the learner’s knowledge state
is represented as a latent variable. This probabilistic
framework predicts whether a learner has mastered a
given KC based on their observed responses to prac-
tice opportunities.
BKT models the learning process as an HMM
with two states as follows:
• Knowledge State (Latent). Whether the learner
has mastered the KC (K
t
= 1) or not (K
t
= 0).
• Observed Performance. Correct (O
t
= 1) or in-
correct (O
t
= 0) response at time t.
For a detailed derivation of the BKT model, see
(Bulut et al., 2023; Corbett and Anderson, 1994). The
model can be defined using the following HMM pa-
rameters:
• P(L
0
): The prior probability of mastery before
any practice.
• P(T ): The learning probability, i.e., the chance of
transitioning from non-mastery (K
t
= 0) to mas-
tery (K
t+1
= 1) after a practice opportunity.
• P(G): The guess probability, i.e., the likelihood
of a correct response given non-mastery.
• P(S): The slip probability, i.e., the likelihood of
an incorrect response given mastery.
The key HMM transitions are as follows:
• Transition from non-mastery to mastery is gov-
erned by P(T ).
• Mastery is assumed to be absorbing: once a
learner masters the KC, they remain in mastery
indefinitely.
BKT assumes that KCs are independent. That is,
the knowledge or mastery of one KC does not influ-
ence another. This assumption simplifies the model
but may not reflect realistic learning scenarios where
skills often interrelate. Moreover, BKT does not
model forgetting behavior, the the likelihood of tran-
sitioning from mastery to non-mastery is zero under
this model.
3.1.1 Forgetting Variant
A common extension to BKT incorporates forget-
ting, where the model allows transitions from mastery
back to non-mastery. Different approaches have been
used to incorporate forgetting to BKT (Pel
´
anek, 2017;
Badrinath et al., 2021). As described in (Khajah et al.,
2016), one approach is to add a new forgetting prob-
ability, P(F), which models the probability of transi-
tioning from mastery to non-mastery as follows:
P(K
t+1
= 0 | K
t
= 1) = P(F) (1)
This variant accounts for scenarios where learned
knowledge decays over time. In this work, we ex-
clusively use this variant, and the term BKT will refer
to this specific version.
3.2 Deep Knowledge Tracing
Deep Knowledge Tracing (DKT) (Piech et al., 2015)
employs a recurrent neural network (RNN), typically
a Long Short-Term Memory (LSTM) network, to pro-
cess sequences of learner interactions and predict fu-
ture performance. Each input sequence consists of in-
teraction pairs (q
t
, y
t
), where q
t
is a single KC in the
original DKT and y
t
is the correctness of the learner’s
response (y
t
= 1 for correct, y
t
= 0 for incorrect).
The RNN processes these sequences to update a
hidden state h
t
, which represents the learner’s evolv-
Sparse Binary Representation Learning for Knowledge Tracing
77

ing knowledge state. The hidden state is updated iter-
atively:
h
t
= f (h
t−1
, x
t
), (2)
where x
t
= (q
t
, y
t
) encodes the interaction at time t,
and f represents the RNN dynamics (e.g., LSTM or
GRU).
Using the updated hidden state h
t
, the model pre-
dicts the probability of a correct response for each
KC:
P(y
t+1
= 1|q
t+1
, h
t
) (3)
This prediction is generated through a fully connected
output layer followed by a softmax activation.
While DKT generally outperforms classical mod-
els such as BKT (Khajah et al., 2016; Gervet et al.,
2020) and makes fewer assumptions about the data,
it has notable limitations. One significant drawback
is its lack of interpretability. Unlike BKT, which pro-
vides clear parameter interpretations, such as learn-
ing and slip probabilities, the hidden state in DKT is
opaque, making it difficult to extract meaningful in-
sights.
Lastly, the original model implementation can suf-
fer from label leakage and requires specialized meth-
ods to be correctly evaluated (Liu et al., 2022). To
avoid this issue, in this paper, q
t
represents the set of
KCs associated with a given question, and x
t
is de-
fined as the mean of the embeddings of these KCs. In
this paper, DKT denotes this variant.
Deep Knowledge Tracing marks a paradigm shift
in knowledge tracing, offering a flexible and pow-
erful approach to modeling student learning. How-
ever, challenges such as interpretability and reliance
on large datasets maintain the relevance of classical
models like BKT. In this paper, we aim to bridge
the gap by transferring the representational strengths
of deep learning to enhance classical models such as
BKT.
In this section, we provide an overview of knowl-
edge tracing models that are relevant to this work.
3.3 Bayesian Knowledge Tracing
Bayesian Knowledge Tracing (BKT)(Corbett and An-
derson, 1994) is formulated as a Hidden Markov
Model (HMM), where the learner’s knowledge state
is represented as a latent variable. This probabilistic
framework predicts whether a learner has mastered a
given KC based on their observed responses to prac-
tice opportunities.
BKT models the learning process as an HMM
with two states as follows:
• Knowledge State (Latent). Whether the learner
has mastered the KC (K
t
= 1) or not (K
t
= 0).
• Observed Performance. Correct (O
t
= 1) or in-
correct (O
t
= 0) response at time t.
For a detailed derivation of the BKT model, see
(Bulut et al., 2023; Corbett and Anderson, 1994). The
model can be defined using the following HMM pa-
rameters:
• P(L
0
): The prior probability of mastery before
any practice.
• P(T ): The learning probability, i.e., the chance of
transitioning from non-mastery (K
t
= 0) to mas-
tery (K
t+1
= 1) after a practice opportunity.
• P(G): The guess probability, i.e., the likelihood
of a correct response given non-mastery.
• P(S): The slip probability, i.e., the likelihood of
an incorrect response given mastery.
The key HMM transitions are as follows:
• Transition from non-mastery to mastery is gov-
erned by P(T ).
• Mastery is assumed to be absorbing: once a
learner masters the KC, they remain in mastery
indefinitely.
BKT assumes that KCs are independent. That is,
the knowledge or mastery of one KC does not influ-
ence another. This assumption simplifies the model
but may not reflect realistic learning scenarios where
skills often interrelate. Moreover, BKT does not
model forgetting behavior, the the likelihood of tran-
sitioning from mastery to non-mastery is zero under
this model.
3.3.1 Forgetting Variant
A common extension to BKT incorporates forget-
ting, where the model allows transitions from mastery
back to non-mastery. Different approaches have been
used to incorporate forgetting to BKT (Pel
´
anek, 2017;
Badrinath et al., 2021). As described in (Khajah et al.,
2016), one approach is to add a new forgetting prob-
ability, P(F), which models the probability of transi-
tioning from mastery to non-mastery as follows:
P(K
t+1
= 0 | K
t
= 1) = P(F) (4)
This variant accounts for scenarios where learned
knowledge decays over time. In this work, we ex-
clusively use this variant, and the term BKT will refer
to this specific version.
3.4 Deep Knowledge Tracing
Deep Knowledge Tracing (DKT) (Piech et al., 2015)
employs a recurrent neural network (RNN), typically
CSEDU 2025 - 17th International Conference on Computer Supported Education
78

a Long Short-Term Memory (LSTM) network, to pro-
cess sequences of learner interactions and predict fu-
ture performance. Each input sequence consists of in-
teraction pairs (q
t
, y
t
), where q
t
is a single KC in the
original DKT and y
t
is the correctness of the learner’s
response (y
t
= 1 for correct, y
t
= 0 for incorrect).
The RNN processes these sequences to update a
hidden state h
t
, which represents the learner’s evolv-
ing knowledge state. The hidden state is updated iter-
atively:
h
t
= f (h
t−1
, x
t
), (5)
where x
t
= (q
t
, y
t
) encodes the interaction at time t,
and f represents the RNN dynamics (e.g., LSTM or
GRU).
Using the updated hidden state h
t
, the model pre-
dicts the probability of a correct response for each
KC:
P(y
t+1
= 1|q
t+1
, h
t
) (6)
This prediction is generated through a fully connected
output layer followed by a softmax activation.
While DKT generally outperforms classical mod-
els such as BKT (Khajah et al., 2016; Gervet et al.,
2020) and makes fewer assumptions about the data,
it has notable limitations. One significant drawback
is its lack of interpretability. Unlike BKT, which pro-
vides clear parameter interpretations, such as learn-
ing and slip probabilities, the hidden state in DKT is
opaque, making it difficult to extract meaningful in-
sights.
Lastly, the original model implementation can suf-
fer from label leakage and requires specialized meth-
ods to be correctly evaluated (Liu et al., 2022). To
avoid this issue, in this paper, q
t
represents the set of
KCs associated with a given question, and x
t
is de-
fined as the mean of the embeddings of these KCs. In
this paper, DKT denotes this variant.
Deep Knowledge Tracing marks a paradigm shift
in knowledge tracing, offering a flexible and pow-
erful approach to modeling student learning. How-
ever, challenges such as interpretability and reliance
on large datasets maintain the relevance of classical
models like BKT. In this paper, we aim to bridge
the gap by transferring the representational strengths
of deep learning to enhance classical models such as
BKT.
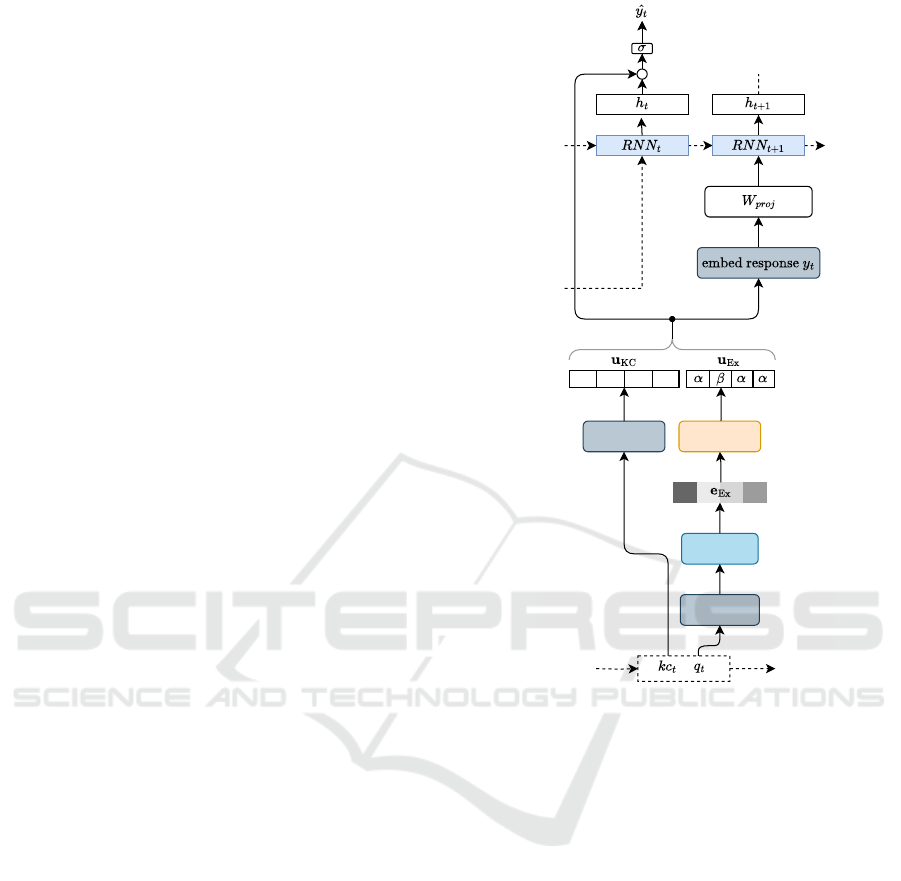
4 MODEL DESCRIPTION
In this section, we present our model for predicting
student responses. The model integrates KCs and ex-
ercise embeddings to capture the temporal dynamics
of student interactions. Central to our approach is
Linear Layer
Quantization
Multi-hot
Embeddings
0
1
0
1
.
Exercise
Embeddings
Figure 1: The overall architecture of the proposed model.
the learning of a binary representation, where each bit
represents the presence or absence of a KC. This bi-
nary representation serves as a multi-hot encoding, a
vector in which multiple positions can be ”hot” (i.e.,
set to one) to indicate the presence of multiple KCs
simultaneously.
The key components of the model include the con-
struction of these binary multi-hot vectors, derived
from KCs and exercise embeddings, a quantization
algorithm for generating the binary vectors, and a pre-
diction mechanism using an RNN. The overall archi-
tecture is described in Figure 1.
4.1 Multi-Hot Encoding of Knowledge
Concepts
Let N be the total number of KCs in the dataset. For
each exercise, we construct an N-dimensional multi-
hot vector u
kc
∈ {0, 1}
N
to represent its associated
KCs. Additionally, we construct a vector u
(kc,y)
that
embeds the correctness label y ∈ {0, 1}, where y = 1
corresponds to a correct response and y = 0 corre-
Sparse Binary Representation Learning for Knowledge Tracing
79

sponds to an incorrect response. The multi-hot vector
u
kc
is defined as:
u
kc
[i] =



1, if the i-th knowledge concept is
associated with the exercise,
0, otherwise.
(7)
Using u
kc
, we construct the final multi-hot vector
u
(kc,y)
as:
u
(kc,y)
= u
kc
· y ⊕ u
kc
· (1 − y), (8)
where ⊕ denotes vector concatenation. This formu-
lation ensures that the first N entries of u
(kc,y)
encode
the KCs for a correct response (y = 1), while the last
N entries encode the KCs for an incorrect response
(y = 0).
4.2 Multi-Hot Encoding from Exercise
Embeddings
Our goal is to map each exercise q to a binary vector,
similar to the KC-based u
kc
, where a value of one in-
dicates the presence of an auxiliary KC and a value of
zero indicates its absence.
4.2.1 Exercise Embeddings and Linear Layer
Each exercise is represented by an embedding vector
x
Ex
∈ R
d
, where d is the dimensionality of the em-
bedding space. The embedding x
Ex
is passed through
a linear layer to obtain a latent representation:
e
Ex
= Wx
q
+ b, (9)
where W ∈ R
M×d
is a weight matrix, b ∈ R
M
is a bias
vector and M is the number of auxiliary KCs. The
output e
Ex
∈ R
M
captures the latent features of the
exercise.
4.2.2 The Quantization Algorithm
The latent vector e
Ex
is transformed into a discrete
vector u
Ex
∈ {α, β}
M
, where the model learns the
scalar values of α and β under the constraint α > β.
In downstream tasks, α represents one, indicating the
presence of an auxiliary KC, and β represents zero,
indicating its absence. Additionally, the representa-
tion is constrained to be sparse, ensuring that only
a few ones appear in the final vector. These ones
correspond to auxiliary KCs in downstream tasks.
Algorithm Steps:
1. Top-C
max
Selection. Identify the indices of the
top C
max
largest values in e
Ex
, denoted as I
top
⊆
{1, 2, . . . , M}. Create a mask m ∈ {0, 1}
M
where:
m[i] =
(
1, if i ∈ I
top
,
0, otherwise.
(10)
This mask will enforce the sparsity constraint in
the next step.
2. Binary Transformation. Rather than using tra-
ditional binary neural network methods such as the
sign function, our method outputs two possible val-
ues at each dimension, denoted by α and β with the
constraint that α > β. To achieve this, we apply the
following discretization function Q to e
Ex
:
Q(e
Ex
) = f (e
Ex
) · m (11)
Here, f is applied element-wise to each dimension
of e
Ex
and is defined as:
f (x) =
(
0, if x ≤ 0,
1, if x > 0.
(12)
Lastly, we apply the following:
u
Ex
= Q(e
Ex
)α + (1 − Q(e
Ex
))β
where β = cσ(p
β
) and α = c(1 + σ(p
α
)). Here, c is
a hyperparameter (set to one in our implementation).
p
α
and p
β
are scalar trainable parameters used to gen-
erate α and β, respectively.
To enable training of this discrete mapping using
stochastic gradient descent, we apply the straight-
through estimator (STE) (Bengio et al., 2013b). In
the forward pass, the quantization algorithm is ap-
plied as described in 4.2.2. In the backward pass,
we modify the gradient by treating the discretization
function Q as the identity function:
∂Q(e
Ex
)
∂e
Ex
= I, (13)
allowing gradients to flow through the discrete opera-
tion.
4.2.3 Embedding Ground-Truth Labels
Similar to how we embed ground truth labels with the
multi-hot KC vector u
(KC,y)
, we construct the vector
u
(Ex,y)
to incorporate the correctness label y by con-
catenating as follows:
u
(Ex,y)
= u
Ex
· y ⊕ u
Ex
· (1 − y) (14)
4.3 Sequence Modeling
At each time step t, we concatenate the labeled multi-
hot vectors u
(KC,y)
and u
(Ex,y)
to form a unified feature
vector v
t
of dimension 2N + 2M:
v
t
= u
(KC,y)
⊕ u
(Ex,y)
(15)
The concatenated vector v
t
is projected into a
dense representation suitable for sequence modeling
through a linear transformation:
z
t
= W
proj
v
t
, (16)
CSEDU 2025 - 17th International Conference on Computer Supported Education
80

where W
proj
∈ R
D×(2N+2M)
is a trainable weight ma-
trix, and z
t
∈ R
D
is the resulting dense feature vector.
To model temporal dependencies, we use an RNN,
which offers a lower computational cost compared to
other sequential models, such as Transformers. The
sequence of dense feature vectors {z
1
, z
2
, . . . , z
T
} is
fed into a recurrent neural network (RNN):
h
t
= RNN(z
t
, h
t−1
), (17)
where h
t
represents the hidden state at time step t.
The hidden state h
t
is subsequently processed
through a linear transformation to produce logits cor-
responding to each KC and auxiliary KC:
o
t
= W
out
h
t
+ b
out
, (18)
where W
out
∈ R
(N+M)×H
is the weight matrix, and
b
out
∈ R
N+M
is the bias vector, both of which are
trainable parameters.
To compute the final prediction, we concate-
nate the binary multi-hot vectors u
KC,t
∈ {0, 1}
N
and
u
Ex,t
∈ {0, 1}
M
:
u
t
= u
KC,t
⊕ u
Ex,t
∈ {0, 1}
N+M
, (19)
where ⊕ denotes the concatenation operation. The
predicted probability of a correct response is then cal-
culated as:
ˆy
t
= σ

u
⊤
t
o
t

, (20)
with σ(·) denoting the sigmoid activation function.
4.4 Application of the Learned Binary
Representation in Downstream
Tasks
The discrete vector u
Ex
can serve as features for
downstream tasks. As it only contains two values
α and β, it can be easily mapped to ones and zeros.
Given that our model is constrained with α > β, we
simply map α to one which denotes an existence of
an auxiliary KC and β to zero to denote the lack of an
auxiliary KC.
5 EXPERIMENTS
In this section, we evaluate the effectiveness of our
proposed model. We compare its performance with
baseline models and demonstrate the utility of the ex-
tracted auxiliary KCs in downstream tasks. All ex-
periments were conducted on publicly available edu-
cational datasets.
5.1 Experimental Setup
5.1.1 Datasets
We use widely used and publicly available datasets
for knowledge tracing:
• ASSISTments2009
1
. It is derived from the
the ASSISTments online learning platform which
was gathered during the school year 2009-2010.
They provide two datasets, the one we used is
called the skill-builder data.
• ASSISTments2017
2
. It is a much recent data
from ASSISTments and it was used for the Work-
shop on Scientific Findings from the ASSIST-
ments Longitudinal Data Competition during the
The 11th Conference of Educational Data Mining.
However, we utilized the publicly available pre-
processed version used in (Ghosh et al., 2020).
• Algebra2005 (Stamper et al., 2010). This dataset
was part of the 2010 KDD Cup Educational Data
Mining Challenge.
• riiid2020 (Choi et al., 2020). It was introduced as
part of a Kaggle competition aimed at improving
AI-driven student performance prediction. The
dataset consists of millions of anonymized student
interactions with an AI-based tutoring system, fo-
cusing on question-solving activities. We choose
a million entry from this dataset.
Detailed statistics can be found in table 1
Table 1: Dataset attributes after prepossessing.
dataset questions KCs students
ASSISTments2009 17751 123 4163
ASSISTments2017 3162 102 1709
Riiid2020 13522 188 3822
Algebra2005 173650 112 574
5.1.2 Baselines
We compare our model against the following baseline
methods:
• Bayesian Knowledge Tracing (BKT)(Corbett
and Anderson, 1994). A probabilistic model that
uses predefined KCs for student modeling.
• Deep Knowledge Tracing with Average Em-
beddings. A neural network-based model that
learns directly from student response sequences
without requiring predefined KCs. To avoid ac-
counting for label leakage we simply average the
1
https://sites.google.com/site/assistmentsdata/home/
2
https://sites.google.com/view/assistmentsdatamining/
Sparse Binary Representation Learning for Knowledge Tracing
81

KC embeddings for all KCs belonging to the same
question.
• Dynamic Key-Value Memory Networks
(DKVMN)(Zhang et al., 2017). employs a mem-
ory network structure with two types of memory:
key memory, representing latent knowledge
concepts, and value memory
• Deep Item Response Theoy (deepIRT)(Yeung,
2019). It incorporate a model similar to DKVMN
with Item Response Theory (IRT) which is a psy-
chometric approach that models the relationship
between student abilities, question difficulty, and
the probability of answering correctly
• Question-Centric Interpretable KT Model
(QIKT)(Chen et al., 2023). Which is another
model that combines IRT with deep learning.
5.1.3 Implementation Details
For our proposed model, we use an embedding size
of d = 32 for both dense and binary exercise embed-
dings, which means we have 32 auxiliary KCs. We
used the Long short-term memory (LSTM) type of
RNN architecture with a hidden size of h = 128. We
use a maximum of C
max
= 4 auxiliary KCs per exer-
cise. We train the models using the Adam optimizer
with a learning rate of 0.001 for all models except
for BKT which we used 0.01 (BKT was trained us-
ing stochastic gradient descent). We used a batch size
of 32 for DKVMN, deepIRT, and QIKT. We used a
batch size of 128 for DKT and BKT. All experiments
were conducted using a dataset split of 80% for train-
ing, 10% for validation, and 10% for testing. We use
the area under the curve (AUC) metric for evaluation.
5.2 Results
5.2.1 Performance Comparison
Table 2 summarizes the performance of our proposed
model in comparison to the baseline methods. The
results indicate that our model consistently outper-
forms all baselines on certain datasets, while achiev-
ing the second-best performance on the remaining
datasets. These findings underscore the efficacy of
our approach, demonstrating that despite the discrete
constraints, our model can surpass others that depend
on dense representations.
5.2.2 Downstream Task Performance with BKT
We assess the utility of the extracted auxiliary KCs
by training BKT and DKT models on these repre-
sentations, as shown in Table 3. The results reveal
that BKT augmented with auxiliary KCs (BKT+aux)
outperforms the standard DKT on both the assist-
ment2009 and riiid2020 datasets. Furthermore, the
inclusion of auxiliary KCs boosts BKT’s performance
across all datasets, although the improvement on the
algebra2005 dataset is minimal. In contrast, DKT
with auxiliary KCs (DKT+aux) achieves better per-
formance on all datasets except algebra2005, where it
underperforms compared to the original DKT.
5.3 Ablation Study
To demonstrate the effectiveness of the quantization
layer, we create three variants:
• SBRKTtanh. This variant adds the hyperbolic
tangent function (tanh) as an activation function to
the linear transformation in 9. The discretization
step maps the output to either -1 or +1 (instead of
α and β).
• SBRKT10. This variant applies a sigmoid activa-
tion to the output of the linear transformation in 9.
Discretization is performed by mapping any value
less than 0.5 to 0, and values greater than or equal
to 0.5 to 1 (instead of α and β).
• SBRKTdense. This variant completely removes
the quantization step, utilizing a dense representa-
tion instead. However, this representation cannot
be directly used in downstream tasks with the ap-
proach outlined in this paper.
As shown in Table 4, the proposed model outper-
formed all other variants, except on the algebra2005
dataset, where it achieved the second-best perfor-
mance with a small difference (0.006). Notably,
Table 2: AUC Scores with Highlighted and Marked Winners and Runners-Up (* Best, ** Second Best).
Model Algebra2005 ASSISTment2009 ASSISTment2017 riiid2020
BKT 0.7634 0.6923 0.6081 0.6215
DKT 0.8198 0.7099 0.6807 0.6503
DKVMN 0.7759 0.7362 0.7169 0.7362**
DeepIRT 0.7750 0.7374 0.7170 0.7360
SBRKT 0.8223** 0.7602* 0.7494** 0.7369*
QIKT 0.8335* 0.7574** 0.7527* 0.7324
CSEDU 2025 - 17th International Conference on Computer Supported Education
82

Table 3: AUC Scores with Winners and Runners-Up Highlighted (* Best, ** Second Best). DKT+aux and BKT+aux refer to
DKT and BKT models augmented with pretrained auxiliary KCs.
Model Algebra2005 ASSISTment2009 ASSISTment2017 riiid2020
BKT 0.7634 0.6923 0.6081 0.6215
BKT+aux 0.7655 0.7325** 0.6760 0.7173**
DKT 0.8198* 0.7099 0.6807** 0.6503
DKT+aux 0.7997** 0.7481* 0.7422* 0.7365*
Table 4: AUC Scores with Highlighted and Marked Win-
ners and Runners-Up (* Best, ** Second Best). algebra05,
assist09, and assist17 correspond to Algebra2005, AS-
SISTments2009, and Assistments2017, respectively. SBR,
SBR10, and SBRtanh represent SBRKT, SBRKT10, and
SBRKTtanh, respectively.
Dataset algebra2005 assist09 assist17
SBR 0.8223** 0.7602* 0.7494*
SBR10 0.8231* 0.7464** 0.7431
SBRdense 0.8122 0.7169 0.7448
SBRtanh 0.8166 0.7449 0.7491**
QCKTdense significantly underperformed compared
to the other models, highlighting the importance of
the quantization step in this architecture.
We also carried out experiments to evaluate the
utility of these variant representations in downstream
tasks. As shown in Table 5, the models that utilize the
auxiliary KCs of SBRKT outperformed all other vari-
ants, except in the algebra2005 data set, where none
of the variants showed significant improvement, and
some even experienced performance drop when aux-
iliary KCs were added.
Table 5: AUC Scores with highlighted and marked winners
and runners-up (* Best, ** Second Best). algebra05, as-
sist09, and assist17 correspond to Algebra2005, ASSIST-
ments2009, and Assistments2017, respectively. +AX10,
+AXtanh means trained with auxiliary KCs from SBRKT10
and SBRKTtanh, respectively.
Dataset algebra05 assist09 assist17
BKT 0.7634 0.6923 0.6081
DKT 0.8198* 0.7099 0.6807
BKT+aux 0.7655 0.7325** 0.6760
DKT+aux 0.7997** 0.7481* 0.7422*
BKT+AX10 0.7745 0.7283 0.6577
DKT+AX10 0.7899 0.7318 0.7301**
BKT+AXtanh 0.6860 0.6736 0.5969
DKT+AXtanh 0.7454 0.6974 0.6722
5.4 Summary of Findings
Our experiments reveal the following key insights:
• The proposed model outperforms the baselines
across multiple benchmarks, despite the sparse
discrete constraints imposed by the architecture
which helped extract further auxiliary KCs.
• The extracted auxiliary KCs can significantly en-
hance downstream tasks. In our experiments,
BKT consistently showed improved performance
when the learned auxiliary KCs were incorpo-
rated across all datasets. However, the same was
not true for DKT. While DKT+aux achieved sub-
stantial performance gains on some datasets (e.g.,
an increase of over 6% in AUC on the Assist-
ment2017 dataset), it underperformed on the al-
gebra2005 dataset.
6 CONCLUSIONS
In this paper, we proposed Sparse Binary Representa-
tion Knowledge Tracing (SBRKT), a model designed
to overcome the limitations of predefined KCs by gen-
erating auxiliary KCs through a learnable sparse bi-
nary representation. Our results demonstrated that
SBRKT achieves competitive performance across
datasets and significantly enhances downstream mod-
els’ capabilities.
In particular, integrating the auxiliary KCs with
Bayesian Knowledge Tracing (BKT) outperformed
the original Deep Knowledge Tracing (DKT) model
on some datasets, while preserving the interpretabil-
ity, which is a hallmark of BKT. The auxiliary KCs
also improved BKT’s predictive performance across
all tested datasets without requiring modifications to
its foundational structure.
Our findings underscore the potential of SBRKT
to address limitations in traditional KT models while
expanding their applicability in real-world educa-
tional scenarios. Future research could explore refin-
ing auxiliary KC generation methods and leveraging
these representations in broader applications for adap-
tive learning and personalized education systems.
ACKNOWLEDGEMENTS
We would like to thank the anonymous reviewers
for their helpful feedback and suggestions. This
Sparse Binary Representation Learning for Knowledge Tracing
83

work was funded by the federal state of Baden-
W
¨
urttemberg as part of the Doctoral Certificate Pro-
gramme ”Wissensmedien” (grant number BW6 10).
REFERENCES
Badrinath, A., Wang, F., and Pardos, Z. A. (2021). pybkt:
An accessible library of bayesian knowledge tracing
models. In Hsiao, S. I., Sahebi, S. S., Bouchet, F., and
Vie, J., editors, Proceedings of the 14th International
Conference on Educational Data Mining, EDM 2021,
virtual, June 29 - July 2, 2021. International Educa-
tional Data Mining Society.
Bengio, Y., Courville, A., and Vincent, P. (2013a). Rep-
resentation learning: A review and new perspectives.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 35(8):1798–1828.
Bengio, Y., L
´
eonard, N., and Courville, A. C. (2013b).
Estimating or propagating gradients through stochas-
tic neurons for conditional computation. ArXiv,
abs/1308.3432.
Bulut, O., Shin, J., Yildirim-Erbasli, S. N., Gorgun, G., and
Pardos, Z. A. (2023). An introduction to bayesian
knowledge tracing with pybkt. Psych, 5(3):770–786.
Chen, J., Liu, Z., Huang, S., Liu, Q., and Luo, W. (2023).
Improving interpretability of deep sequential knowl-
edge tracing models with question-centric cognitive
representations. Proceedings of the AAAI Conference
on Artificial Intelligence, 37(12):14196–14204.
Choi, Y., Lee, Y., Shin, D., Cho, J., Park, S., Lee, S., Baek,
J., Bae, C., Kim, B., and Heo, J. (2020). Ednet: A
large-scale hierarchical dataset in education. In Inter-
national Conference on Artificial Intelligence in Edu-
cation, pages 69–73, Morocco. Springer.
Corbett, A. T. and Anderson, J. R. (1994). Knowledge trac-
ing: Modeling the acquisition of procedural knowl-
edge. User modeling and user-adapted interaction,
4:253–278.
Gervet, T., Koedinger, K., Schneider, J., Mitchell, T., et al.
(2020). When is deep learning the best approach to
knowledge tracing? Journal of Educational Data
Mining, 12(3):31–54.
Ghosh, A., Heffernan, N., and Lan, A. S. (2020). Context-
aware attentive knowledge tracing. In Proceedings
of the 26th ACM SIGKDD International Conference
on Knowledge Discovery & Data Mining, KDD ’20,
page 2330–2339, New York, NY, USA. Association
for Computing Machinery.
Khajah, M. M., Lindsey, R. V., and Mozer, M. C.
(2016). How deep is knowledge tracing? ArXiv,
abs/1604.02416.
Li, L. and Wang, Z. (2023). Calibrated q-matrix-
enhanced deep knowledge tracing with relational at-
tention mechanism. Applied Sciences, 13(4):2541.
Liu, Y., Yang, Y., Chen, X., Shen, J., Zhang, H., and
Yu, Y. (2020). Improving knowledge tracing via
pre-training question embeddings. arXiv preprint
arXiv:2012.05031.
Liu, Z., Liu, Q., Chen, J., Huang, S., Tang, J., and Luo,
W. (2022). pykt: A python library to benchmark
deep learning based knowledge tracing models. In
Advances in Neural Information Processing Systems,
volume 35, pages 18542–18555. Curran Associates,
Inc.
Nakagawa, H., Iwasawa, Y., and Matsuo, Y. (2018). End-
to-end deep knowledge tracing by learning binary
question-embedding. In 2018 IEEE International
Conference on Data Mining Workshops (ICDMW),
pages 334–342. IEEE.
Pel
´
anek, R. (2017). Bayesian knowledge tracing, logistic
models, and beyond: an overview of learner modeling
techniques. User Model. User Adapt. Interact., 27(3-
5):313–350.
Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M.,
Guibas, L. J., and Sohl-Dickstein, J. (2015). Deep
knowledge tracing. Advances in neural information
processing systems, 28.
Stamper, J., Niculescu-Mizil, A., Ritter, S., Gordon, G.,
and Koedinger, K. (2010). [data set name]. [chal-
lenge/development] data set from kdd cup 2010 edu-
cational data mining challenge. Retrieved from http://
pslcdatashop.web.cmu.edu/KDDCup/downloads.jsp.
Wang, W., Ma, H., Zhao, Y., and Li, Z. (2024). Pre-training
question embeddings for improving knowledge trac-
ing with self-supervised bi-graph co-contrastive learn-
ing. ACM Transactions on Knowledge Discovery from
Data, 18(4):1–20.
Wang, W., Ma, H., Zhao, Y., Li, Z., and He, X. (2021).
Relevance-aware q-matrix calibration for knowledge
tracing. In Artificial Neural Networks and Machine
Learning–ICANN 2021: 30th International Confer-
ence on Artificial Neural Networks, Bratislava, Slo-
vakia, September 14–17, 2021, Proceedings, Part III
30, pages 101–112. Springer.
Wang, W., Ma, H., Zhao, Y., Li, Z., and He, X. (2022).
Tracking knowledge proficiency of students with cal-
ibrated q-matrix. Expert Systems with Applications,
192:116454.
Yeung, C. (2019). Deep-irt: Make deep learning based
knowledge tracing explainable using item response
theory. In Proceedings of the 12th International
Conference on Educational Data Mining, Montr
´
eal,
Canada. International Educational Data Mining Soci-
ety (IEDMS).
Zhang, J., Shi, X., King, I., and Yeung, D. (2017). Dynamic
key-value memory networks for knowledge tracing.
In Proceedings of the 26th International Conference
on World Wide Web, pages 765–774, Perth, Australia.
ACM.
CSEDU 2025 - 17th International Conference on Computer Supported Education
84