Convolutional Neural Networks Enriched by Handcrafted Attributes

(Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

Luiz Fernando Segato dos Santos

, Leandro Alves Neves

1 b

, Alessandro Santana Martins

2 c

Guilherme Freire Roberto

, Tha´ına Aparecida A zevedo Tosta

4 e

and Marcelo Zanchetta do Nascimento

Department of Computer Science and Statistics (DCCE), S˜ao Paulo State University (UNESP),

S˜ao Jos´e do Rio Preto, Brazil

Federal Institute of Triˆangulo Mineiro (IFTM), Ituiutaba, Brazil

Institute of Mathematics and Computer Science (ICMC), University of S˜ao Paulo (USP), S˜ao Carlos, Brazil

Federal University of S˜ao Paulo (UNIFE SP), S˜ao Jos´e dos Campos, Brazil

Faculty of Computer Science (FACOM), Federal University of Uberlˆandia (UFU), Uberlˆandia, Brazil

Keywords:

Enriched Backpropagation, Fractal Techniques, Loss Functions, CNN Architectures, H&E Images.

Abstract:

This paper presents a novel method called Enriched-CNN, designed to enrich CNN models using handcrafted

features extracted from multiscale and multidimensional fractal techniques. These features are incorporated

directly into the loss function during model training through speciﬁc strategies. The method was applied to

three important histological datasets for studying and classif ying H&E-stained samples. Several CNN archi-

tectures, such as ResNet, InceptionNet, EfﬁcientNet, and others, were tested to understand the enrichment

behavior in different scenarios. The best results achieved accuracy rates ranging fr om 93.75% to 100% for

enrichment situations involving only 3 to 5 features. This paper also provides signiﬁcant insights into the

conditions that most contributed to the process and allowed competitiveness compared to the specialized liter-

ature, such as the possibility of composing models with minimal or no structural changes. This unique aspect

enables t he method to be applied to other types of neural architectures.

1 INTRODUCTION

Enriching co nvolutional models have been explored

and applied in histopathological con texts to improve

diagnostic su pport systems and pattern recognition

(Roberto et al., 2021; Longo et al., 2023; Tengu am

et al., 2024). This approa ch ha s yielded various b e n-

eﬁts, such as improving model performanc e or re-

solving training issues like overﬁtting (Jaha n et al.,

2022). Some studies combine different types of at-

tributes aiming to enrich their models. The most well-

https://orcid.org/0009-0008-0851-4379

https://orcid.org/0000-0001-8580-7054

https://orcid.org/0000-0003-4635-5037

https://orcid.org/0000-0001-5883-2983

https://orcid.org/0000-0002-9291-8892

https://orcid.org/0000-0003-3537-0178

known attributes in this context are handcrafted and

deep-lear ned.

Among handcrafted attributes, appr oaches based

on multiscale and/or multidimensiona l fractal tech-

niques stand out, especially in the histop athology ﬁeld

(Roberto et al., 2021; Ivanovici and Richard, 2011).

Deep-learned attributes, on the other hand, include

those obtain ed through convolutional neural networks

(CNN) (Nanni et al., 20 20). For instance, network

models are applied to image samples, and the val-

ues obtained during training enable the formation of

feature vectors. It is also crucial to highlight that

the training of these neural networks an d the opti-

mal representation o f data are facilitated by an algo-

rithm known as backpropagation, which strengthens

the most relevant weights throughout training. During

this stage, a cost function, also known as loss fun c-

tion, generates a scalar value indicating how well a

Santos, L. F. S., Neves, L. A., Martins, A. S., Roberto, G. F., Tosta, T. A. A. and Zanchetta do Nascimento, M.

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in Histological Images.

DOI: 10.5220/0013277300003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 467-478

ISBN: 978-989-758-749-8; ISSN: 2184-4992

467

sample is classiﬁed. This value can be minim iz ed or

maximized by an optimizer, depending on the training

objective.

Some combina tions have integrated ha ndcrafted

and deep-lear ned attributes (Nanni et al., 2020).

These combinations have contributed to various ar-

eas (Zheng et al., 2 023), but some challenges still

persist, such as providing appropriate dimensions and

scale for the involved attributes (Cheng et al., 2023)

or preventing redundancy in combining handcrafted

and deep-learned features (Zhe ng et al., 2023). To ad-

dress these divergences in the combination process,

some modiﬁcations in the architectures are required,

resulting in more complex models with speciﬁc ad-

justments for each arc hitecture type (Zheng et al.,

2023).

On the other hand, enrichment can also be ex-

plored through backpropagation. This process o ffers

several strategies tha t incorporate rewards or penalties

directly into the loss function, depending on the train-

ing objective. The possible types of incorporation

into th e loss function primarily occur through sum-

based rules (Hosseini et al., 2023 ) or weighted sum -

based rules (Wu et al., 2023). The in formation incor-

porated in this process is usually backpropag a te d to

the n etwork to update the model weights (Diao et al.,

2023). Despite contributions on the topic in the med-

ical imaging ﬁeld (Diao et al., 20 23), there is no re-

search that has explored model enric hment through

fractal descriptor s directly in the loss function to in-

vestigate model performance and training behavior.

Therefore, researching how mo dels could be en-

riched using handcrafted features such a s multiscale

and multidimensional fractal attributes, as well as

through the loss function, and explor ing the poten-

tial forms of enrichment, including multiple attribute

combinations, is yet to be explored in the literatu re.

1.1 Research Directions and

Contributions

Research has indicated that combining distinct at-

tributes, such as deep-learn e d and hand crafted fea-

tures, is a crucial path to improving pattern recog-

nition systems, regardless of the application context

(Roberto et al., 2021; Nanni et a l., 2020 ). This is par-

ticularly evident when different attribute sources are

considered (Sukegawa et al., 2022). However, despite

attention modules and a dditional data fusion mecha-

nisms improving results (Montalbo, 2022), the mod-

els developed using these strategies still have limita-

tions (Zheng et al., 2023).

Alternatively, model enrichment research, primar-

ily through backpropagation, has overcome some of

these limitations, such as information red undancy

from fea ture fusion proce sses and the incompatibil-

ity of feature dimensions and scales (Xu et al., 2022),

using less c omplex models and achieving promising

results. Moreover, backpropagation studies have en-

abled improvements in distinction rates and reduced

training costs (X u et al., 202 2), leading to advance-

ments in addressing vanishing g radient issues (Hu

et al., 2021) and overﬁtting, e specially in the pres-

ence of class imbalance (Zhang et al., 2024) . Dif-

ferent types of loss func tions have also been consid-

ered for various scenarios, contributing distinctively

to model enrichment (Xu et al., 2022; Zha ng et al. ,

2024).

When handcrafted fe atures are incorporated into

these functions throu gh speciﬁc rules, such as

weighted sum -based rules (Xu et al., 2022), the re-

sults have been encouraging. However, in the his-

tological context, inco rporating these impo rtant fea-

tures directly into the loss function h as not been in-

vestigated. Furthermore, these studies have not di-

rectly incorporated handcrafted attributes into the loss

function but rather utilized domain metrics like retain-

ing edge information ( Edge Loss) an d reducing im -

age distortion (MSE Loss) during le arning (X u et al.,

2022). T hese strategies represent more generic in-

formation in medical images, particularly histological

images where pathologists explore patter ns like cell

clustering.

This raises a fundamen ta l question: how would

model learning be affected if it is enriched with at-

tributes that are more aligned with the nature of his-

tological images? This question serves as the primary

motivation for this stud y. Additionally, using domain-

speciﬁc k nowledge descriptors, such as multiscale

and multidimen sio nal fractals, has helped overcome

numerous challeng es f or this type of scenario (Ten-

guam et al., 2024; Longo et al., 2023). There-

fore, studying these descriptors and their incor pora-

tion rules could enable investigations into new combi-

nations between distinct feature groups. These com-

binations and their rules rep resent signiﬁcant frontiers

in the m achine learning ﬁeld and enhance diagnostic

support systems.

In light of the above, the main contributions of this

study are:

• A new m ethod (Enriched-CNN) capable of en-

riching CNN models throu gh loss function s us-

ing multiscale and multidimensional fractal at-

tributes;

• Insights into the primary conditions and enrich-

ment rules based on various neural architectures

such as ResNet, InceptionNe t, DenseNet, VG-

GNet and EfﬁcientNet;

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

468

• App lica tion of the meth od in relevant histological

dataset representing breast cancer, colorectal can-

cer and liver tissue, providing inf ormation on the

best enriched models and the necessary conditions

for their study and classiﬁcation.

2 METHODOLOGY

The proposed approach was d ivided into two stage s to

explore different enrichment strategies through ha nd-

crafted attributes. Stage 1 aims to extract local and

global fractal attributes from each input image using

multidimen sio nal techniques like Fractal Dimension

(D), Lacunarity (Λ) and Percolation (PERC). Stage 2

investigates the inﬂuence of primar y enrichment rules

through fracta l attributes on the indicated architec-

tures.

2.1 Stage 1 - Multiscale and

Multidimensional Fractal Attributes

Various fractal techniques are available in the litera-

ture for image investigations. This study focuses on

techniques from a multidimension a l and multiscale

perspective, such as probabilistic fractal dimension

(Ivanovici and Richard, 2 011), lacunarity (Ivanovici

and Richard, 2009), and fractal percolation (Roberto

et a l., 2017), as these techniques provide complemen-

tary quantiﬁcations for colored images. The details

are presente d in the following subsections.

2.1.1 Probabilistic Approach-Based Fractal

Dimension

Fractal dimension (D) was calculated ba sed on the ap-

proach described by (Ivanovici and Richard, 2011).

Given a colored RGB input image, each image pixel

is r e presented by a 5D vector (x, y, r, g, b), where spa-

tial c oordina tes (x, y) have colo r components (r, g, b).

Then, a hypercube of side L is initially positioned

in the upper-left corner of the image. On each iter-

ation, this hypercube is dislocated from left to right

and from top to bottom, covering all pixels in a pro-

cess known as gliding-box (Ivanovici and Richard,

2011). The hypercube size is increased when the

analysis reaches the lower-right corner of the im-

age. For each displacement, an analysis is per-

formed comparing the pixels contained within the hy-

percub e . To do this, the central pixel of the hyper-

cube, F

= f (x

, y

, r

, g

, b

), is ﬁxed, and a com-

parison is ma de with the rest of the pixels, includ-

ing the ce ntral pixel itself, using a distance measure

∆. The pixels analyzed in this process are d eﬁned as

= f (x

, y

, r

, g

, b

). In this approach, the analysis is

done through the Minkowski distance (∆

mink

), c alcu-

lated as Equation (1):

∆

mink

= max (|F

) − F

)|), k ∈ r, g, b. (1)

In this process, each pixel F

with a distance ∆ less

than or equal to the scale size L is labelled as 1, indi-

cating it belongs to the hypercube. Otherwise, it is

labelled as 0. By counting these pixels, it is possible

to co nstruct the probability matrix P (m, L) (Ivanovici

and Richard, 2011), which characterizes the p robabil-

ity of m points being co ntained within the hypercube

of side L.

With the construction of the P(m, L) matrix, we

can obtain the partial fractal dim ension N(L), which

is a ssoc ia ted with each hyp e rcube size as deﬁned by

the Equation (2):

N(L) =

∑

m=1

P(m, L)

. (2)

To obtain D, after calculating the N(L) value for

each L, the angular coe fﬁcient of the linear regression

deﬁned by log L × log N(L) enables us to obtain the

probabilistic fractal dimension of the image.

2.1.2 Lacunarity

The multidimensional and multiscale method for cal-

culating the LAC (Λ) of the images un der inves-

tigation was based on the approach by Ivanovici

(Ivanovici and Richard, 2009), using the same prob-

ability matrix for the fractal dimension as described

in subsection 2.1.1. The metric was based on the ﬁrst

and second- order moments, as d e ﬁned by Equ ations

(3) and (4). The LAC (Λ) as a function of L, Λ(L),

was obtained from the distribution measure indicated

in Equation (5).

λ(L) =

∑

m=1

mP(m, L). (3)

(L) =

∑

m=1

P(m, L). (4)

Λ(L) =

(L) − (λ(L))

(λ(L))

. (5)

2.1.3 Multidimensional and Multiscale

Percolation

Multidimensional and multiscale percolation (PERC)

was calculated following the strategy outlined in

(Roberto et al., 2017). To do th is, percolation theory

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

469

was a pplied to analyze pixel paths between one end of

the image and the other. The metho d we used consid-

ers a multiscale approach using the gliding-box tech-

nique. Initially, hypercubes were deﬁned with L = 3.

This parameter is increased by two units after cross-

ing the whole image from the top left to the bottom

right. The relatio nship between the number of hype r-

cubes T that have crossed an image with height H and

width W , as a function of L, is given by:

T (L) = (H −L + 1) × (W −L +1), L ≤ min(H, W).

(6)

For each hypercube of size L, we applied a mul-

tidimensional approach similar to th e one describ ed

in (Ivanovici and Richard, 2 011) in subsection 2.1. 1.

Therefore, when the distance ∆ has a value less than

or equal to L, the pixel P is labelled as - 1, indicat-

ing it represents a pore. Otherwise, it is labelled as 0,

considered the background of the image.

Based on these co mparisons, several clusters were

formed, as described in (Roberto et al., 2017). From

this process, we extracted three functions: th e average

number of clusters C; the ratio of percolating boxes

Q; and the average coverage of the largest cluster M.

To calculate the average numbe r of clusters per box

C(L), we utilized the number of clusters in a single

box (c

), as a function of scale L, divided by the total

number of boxes, as shown in the equation:

C(L) =

∑

T (L)

i=1

T (L)

. (7)

The ratio of perco lating boxes Q was obtained by

counting the number of percolating boxes based on

scale L. A box q

is considered pe rcolating if the ratio

between the number of p ixels labe lled as pores ( Ω

)

and the total number of pixels within the box (L

) ex-

ceeds a percolation threshold p, deﬁned as 0.59275

(Roberto e t al., 2017). The ratio of perco la ting boxes

as a function of L, (Q(L)), was obtained by dividing

the total number of percolating boxes q

by the total

number of boxes T in a scale L. The expression is

given in Equation (8):

Q(L) =

∑

T (L)

i=1

T (L)

. (8)

Finally, the average coverage ra tio of the largest

cluster (M) was calculated by identifying the coverage

ratio of the largest cluster in each box evaluated at

scale L, as shown in Equation (9), whe re γ

represents

the largest cluster in a box i.

M(L) =

∑

T (L)

i=1

T (L)

. (9)

2.1.4 Local and Global Attributes

The fractal descriptors based on the pr obabilistic frac-

tal dimension, lacunarity and percolation appro aches

were calculated with scale variations L, using the

gliding-box method. In these cases, L

max

= 41 was

considered (Roberto et al., 2021), allowing for quan-

tiﬁcation of 20 different scales. The quantiﬁcations

used in this study resulted in a set of 100 local at-

tributes (L ) for each input image. This enabled us

to deﬁne characteristic curves as a function of each

attribute and the scale L. Therefore, for lacunarity,

the curves were formed b ased on the local values as

a fu nction of the sliding hypercube dimension. In the

percolation approach, the curves obtained were C, Q

and M, re presenting percolating r egio ns. The LAC

and PERC cu rves were represented by scalar values to

form attribute vectors. Based on these curves, the fol-

lowing metrics were extracted to g e nerate global at-

tributes: area under the curve (A), skew ness (S), area

ratio (Γ) and maximum point (MP) (Roberto et al.,

2017).

The total number of attributes was dependent

on each category investigated in th is study. Table

1 presents the distribution of handcrafted attributes,

comprising a structure of 116 attributes (T ), with 100

local (L ) and 16 global (G ), calculated as a func-

tion of distance ∆. Global and local attribute sets

were analyz ed to understand enrichment using differ-

ent strategies, as described in the next sections.

2.2 Stage 2 - Enrichment Strategies

To apply the enrichment strategies, some models were

obtained using transfer learning, which reduces the

training tim e of the CNN model and enables analysis

involving datasets with a smaller number of samples.

Therefore, in this proposal, pre-trained networks in

the ImageNet dataset were used (Roberto et al., 2021;

Almaraz-Dam ia n et al. , 2020). Examples of architec-

tures that can be investigated are VGGNet, Inceptio n,

ResNet, EfﬁcientNet, DenseNet and others. Some of

these architectures have already shown relevant re-

sults in medical image classiﬁcation problems in var-

ious contexts (Rajinikanth et al., 2020) and also in the

classiﬁcation of histological images (Tenguam et al.,

2024; Longo et al., 20 23; de Oliveira et al., 2023).

These models were treated as the basis for enrichment

and there fore nam ed as baseline, and were deﬁn ed ac-

cording to r ecommendations available in the literature

(Tenguam et al., 2024 ; L ongo et al., 2023; de Oliveira

et al., 2023).

The enr ic hment process consists o f incorporat-

ing fractal attributes into the loss function through

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

470

Table 1: Identiﬁcation of the attribute name and the total number of handcrafted at tributes.

Attribute Number of Attributes Sets

PERC - C, Q, M 60

Local (L )LAC 20

Local D 20

PERC metrics - C, Q, M 12

Global (G )

LAC metrics 4

Total Number of Attributes 116 All (T = L ∪ G )

different strategies of selection and normalization.

Starting from a de ﬁned architecture f or the base-

line model, some layers are released f or enrichmen t.

The weights of these layers are updated during tr ain-

ing, which, th rough backpropa gation, inc orporates

the co rresponding handcrafted features for each batch

of trained samples (batch size = 32). At the end, the

baseline model beco mes an enriched model. Incor-

poration of features is contingent on th e number of

features selected. For instance, if the ReliefF algo-

rithm identiﬁes and c hooses only the 3 most per tinent

features from the overall feature set, training then pro-

ceeds by processing each given batch of samples ex-

clusively with these 3 selected features while also ap-

plying a deﬁned inc orporation strategy, such as calcu-

lating the mean of their values. This approach allows

for the progressive enrichment of the model as it en-

counters each batch of data across its multiple training

iterations.

2.2.1 Preparation of Handcrafted Features for

Incorporation

In this stage, normalization, selection an d attribute in-

corporation into the loss function (L ) processes were

established for enrichment. The normalization pro-

cess was applied to the handcrafted fractal attribute

set T . Initially, we tested two nor malization types:

min-max (deﬁned by Equations (10) an d (11)) and z-

score (deﬁned by Equation (12)). Normalization is

important to ensure that attributes are correctly in-

corporated, as their value range differs from the loss

function where incorporation occurs. Additionally,

this strategy strengthens the proposed enrichment ap-

proach because it avoids structural m odiﬁcations or

extensions in the ar chitectures, which can lead to di-

mensional incompatibilities (Cheng et al., 2023). It

also minimizes phenomena such as information re-

dunda ncy (Zheng et al., 2023) and other limitations

that often require new modiﬁcations or adjustments

tailored to e ach architecture.

− min(T )

max(T ) − min(T )

ε, (10)

where T

∈ T and

represents each element T

normalized by min-max according to the scale o f val-

ues ε pr ovided by th e loss function.

ε = (max(L ) − min(L)) + min(L ). (11)

− T

, (12)

where T

∈ T and

represents each element T

normalized by z-score, T

is the mean of the T and

is its stand ard deviation.

The normalized attributes

T were subjected to

a selection process using the ReliefF algorithm

(Kononen ko et al., 1997), resulting in a vector

Several selection tests were perform ed with the best

values presented in the results section. This strategy

allowed us to obtain the most relevant descriptors, en-

hance model in te rpretability and indicate which rules

apply to enrichment through different attributes.

To incorporate the normalized and selected at-

tributes

into the model, some adjustments were

made since the loss function only accepts scalars.

Some strategies were implemented, such as averag-

ing the values (

) and applying norms to feature

vectors (k

) with p = {1, 2}, as tested according

to Equation (13):

L = Error(y

, ˆy

) + αk

, (13)

where α is a relevance coefﬁcient that accounts for

normalized fractal attributes. In this study, we con-

sidered α = 1.

2.3 Comparisons and Tests

The enrichment process was tested on the ResNet, In-

ceptionNet, DenseNet, EfﬁcientNet and VGGNet ar-

chitectures acr oss different layers. First, we analyzed

which layers in these arc hitectures contained trainable

parameters. Then, enrichment was applied in a com-

bined manner across the layers. Each combination

resulted in a new enriched CNN mo del (Enriched-

CNN). The goal of this test was to identify the

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

471

most suitable lay er combinations for each architec-

ture, considering co mmonly used performance eval-

uation and validation methods in the literature, such

as accuracy (Acc), cross-validation, and others (Mar-

tinez et al., 2003). The results of the en riched models

were comp ared to those of baseline models to validate

the proposed approach.

Additionally, the mo dels enriched using multi-

scale and multidimensional fractal attributes were

compare d to the classiﬁcation results of these at-

tributes using conventional mach ine learning algo-

rithms representing d ifferent categories, such as

SVM, Random Forest, KNN and Naive Bayes

(Ponti Jr, 2011). Comp arisons between the proposed

models were conducted using the histological d atasets

described in the next sub section.

2.4 Application Context - Histological

Image Datasets

Histological image datasets, especially those stained

with Hematoxylin & Eosin (H&E ), are essential for

training CNN models to create classiﬁcation systems.

However, these da tasets have some limitations, such

as limited availability and diversity of samples, mak-

ing it challenging to train these mo dels for patter n

recogn ition. This requires solutions like enrichment

through handcraf te d f e atures (Dia o et al., 2023). In

the co ntext, the effects a nd conditions imposed to val-

idate the proposed enrichment approa ch were tested

on several datasets, including Colorectal (CR) (Sir-

inukunwattana et al., 2017), Brea st (UCSB) (Gelasca

et a l., 2008) a nd Liver tissue (LG) (Zahn et al., 2007).

Examples from each dataset group (CR, UCSB and

LG) are shown in Figures 1 to 3, respectively. Further

informa tion on the datasets is provided in Table 2.

3 RESULTS AND ANALYSIS

The proposed enrichment was implemented in

the indicated architec tures (ResNet, InceptionNet,

DenseNet, VGGNet and EfﬁcientNet) and applied to

the following H&E datasets: CR, L G and UCSB. Fol-

lowing subsection 2 .2, the pre-trained CNN models

underwe nt normalization and feature selection steps

before incorporating handcrafted features. The Reli-

efF algorithm was used fo r the selection process with

the following feature count (para meter σ): 1, 3, 5, 10

and 20. These parameters were deﬁned based on ob-

servations from relevant studies exploring this algo-

rithm in the histological context (Longo et al., 2023).

All tests were run three times, and the average of the

results was considered when c omparing the architec-

tures a nd datasets. The results were de ﬁned through

samples for training (70%) and testing (30%), using

the holdout cross-validation method. In this study, we

considered a ﬁxed learning rate at 1e

−3

Firstly, we tested the min-max n ormalization. All

attribute incorporation strategies into the lo ss function

were applied (

, p = 1 and p = 2). After apply-

ing the e nrichmen t method with the deﬁned strategies

for each σ value, considering the CR dataset, we ob-

served that except for the ResNet50 architecture, the

enriched model achieved higher Acc rates, with the

highest value at 100%, obtained using σ = 10 and

p = 2, provided by the EfﬁcientNetB2 architecture,

as well as σ = 20 and p = 2 using the VGG19 archi-

tecture, outperforming the baseline models.

When testing the z-score normalization strategy

under the same conditions as the min-max, as shown

in Table 3, the results indicated that the highest Acc

rate (100%) was achieved with EfﬁcientNetB2 using

σ = 10 and VGG19 usin g σ = 5. The most effec-

tive in c orporation was obtained using the vector norm

with p = 2. In turn, the highest average Acc value

(96.73%) was achieved with

incorporation using

σ = 10. Notably, this norm a lization strategy o utper-

formed the baseline models in various combina tions,

namely σ = 10 and p = 2; σ = 3 and p = 1; and, ﬁ-

nally, σ = 1 and σ = 10 using

. This indicates that

the z-score normalization strategy was more efﬁcient

in enriching models based on the ResNet50 architec-

ture. In contrast, this only occur red in one situation

(σ = 1 and p = 1) using the min-max strategy. There-

fore, it is clear that normalization strategies are im-

portant in the context of enriching CNN models using

handcr a fted attributes.

For the LG and UCSB datasets, the enrichment

process exh ibited different behaviors co mpared to the

CR dataset. The same norma lization, selection and

feature incorporation steps were performed for the LG

and UCSB datasets with notab le results hig hlighted in

Tables 4 and 5, respectively.

In the LG dataset, some of the most signiﬁcant

results were achieved with the vector norm strategy

(p = 2) and min-max normaliza tion. This com bina-

tion achieved the highest average Acc rate among the

architecture s (88.78% with σ = 10). In terms of the

highest Acc value, different combina tions of normal-

ization, feature selection and incorporation strategies

achieved the 100 % value using the EfﬁcientNetB2 ar-

chitecture, similar to the CR dataset. Furthermor e ,

the re sults obtained with this dataset indicated th at en-

richment was more efﬁcient than with th e CR dataset,

as the proposed models outperformed baseline mod-

els in most combinations.

In the UCSB dataset, in contrast to CR an d LG, the

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

472

(a) (b)

Figure 1: Examples of H&E colorectal images: (a) benign and (b) malignant.

(a) (b)

Figure 2: Examples of H&E breast images: (a) benign and (b) malignant.

(a) (b)

Figure 3: Examples of H&E liver images: (a) male and (b) female.

winning combination in terms of the highest average

Acc rate was vector norm incorporation (p = 1) with

z-score normalization. This combination achieved

the highest average Acc rate among the ar chitec-

tures (78.33% with σ = 3). The hig hest Acc value

(93.75%) was achieved using p = 1, z-score and the

VGG19 architecture, as well as p = 1, min-max and

EfﬁcientNetB2, an d also

, min-max and VGG19.

The results su ggest that, except for the ResNet50

architecture , en riched models outperformed baseline

models in a ll strategies for the CR and LG da ta sets,

especially for th e UCSB dataset. This is a signiﬁcant

contribution, as histological datasets often have lim-

ited samp le s, par ticularly the UCSB dataset with only

58 samples, which generally hinders the training of

traditional CNN models.

Another noteworthy point is that th e enrichment

behavior differed dep ending on the image dataset

used. Among the incorpor ation strategies, vector

norm with p = 2 for the CR dataset and p = 1 for the

UCSB dataset sto od out. In the LG d ataset, no par-

ticular strategy stood out. Regarding normalization

strategies, their importance was evident in the enrich-

ment process throug h backpropaga tion. Additionally,

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

473

Table 2: Information on the studied datasets.

Dataset Description Classes Total Images Dimensions (pixels)

CR Colorectal tissue 2 165 (91+ 74) 567 × 430 to 775 × 522

UCSB Breast tissue 2 58 (3 2+26) 896 × 768

LG Liver tissue 2 265 (150+115) 417 × 312

Table 3: Acc rates (%) of enriched models compared to baseline models for various CNN architectures, considering the CR

dataset, z-score normalization and feature incorporation using the vector norm with p = 2.

CNN Architectures

Enriched-CNN (z-score)

baseline model

σ = 1 σ = 3 σ = 5 σ = 10 σ = 20

ResNet50 55.10 65.99 66.67 81.63 55.10 99.32

InceptionV3 97.96 98.64 97.28 97.96 97.28 93.88

DenseNet121 97.96 97.28 97.28 98.64 97.28 96.60

EfﬁcientNetB2 97.28 98.64 97.28 100 97.96 90.48

VGG19 97.96 98.64 100 97.28 99.32 91 .16

Average ±

89.25 ±

0.19

91.84 ±

0.14

91.70 ±

0.14

95.10 ±

0.08

89.39 ±

0.19

94.29 ±

0.04

the min-max strategy yielded better results for the LG

dataset, while the z-scor e strategy was prominent for

other datasets. Regarding selection strategies, while

no commonalities em erged across datasets, strategies

involving few attributes (σ = 1 or σ = 3) consistently

produced considerable performance in several situa-

tions. This behavior could be due to the enrichment

process, whic h performe d better in more challeng-

ing circumstances, as observed for the UCSB dataset.

When σ = 1, it is imp lied that a single attribute is ca-

pable of p romoting the necessary enrichment for the

model. This highlig hts the imp ortance of the selection

strategies discussed here, further undersco ring the in-

novation of the prop osed enrichment m e thodology as

a method for en hancing classiﬁcation systems and as-

sisting resear c hers in this ﬁeld.

It is worth noting that training the enriched CNN

models involved enrichment across various layers to

identify the combinations yielding the best results, as

discussed in section 2.3. Tests were perfor med on dif-

ferent layers of the indicated architectures. The best

results are presented in Tables 3 to 5 for the three

datasets studied. The layers achieving these best per-

formances for each architecture are listed in Table 6.

To be tter understand the enrichment proc ess in

machine learning contexts, comparisons were made

among models obtained through classiﬁcation algo-

rithms, as described in subsection 2.3. The algo-

rithms used were SVM, Random Forest, Naive Bayes

and KNN. These algorithms were combined in an en-

semble decision process (Longo et al., 2023). Ad-

ditionally, another combination known as ensemble

descriptors was implemented. I n this approa ch, frac-

tal attributes w e re concatenated with deep-learned at-

tributes extracted from the retrained baseline model

based on the last fully connec ted layer. This layer

selection was based on investigations and relevant re-

sults achieved in the context of histological images

(Tenguam et al., 2024 ; L ongo et al., 2023; de Oliveira

et al., 2023). This strategy also acted as a form

of CNN model enrichment (Tenguam et al., 2024 ;

de Oliveira et al., 2023; Roberto et al., 2021). The

fractal descriptors used here w e re the same as those

used in the previously presented enriched models.

This comparison is presented in Ta ble 7 for σ ≥ 5 val-

ues, with the best results highlighted in bold.

The results indicate that the proposed enrichment

method ou tperformed, in most situations, traditional

training with common classiﬁers in machine learning

processes fo r all datasets tested. Notably, there were

some instances where the enr ic hment showed less sig-

niﬁcant p e rformance, particularly for the ResNet50

architecture . This could be attributed to the residual

connection mec hanism implemented in this architec-

ture.

When σ = 5 and σ = 10, the proposed enrich-

ment method showed noticeable improvements, par-

ticularly for the CR dataset. While no overall ad-

vantages emerged for other datasets, the prop osed

method outperformed en semble models in most sit-

uations when EfﬁcientNetB2 and VGG19 arc hitec-

tures were considered. This comparison served only

to evaluate the feasibility of the proposal, as the im-

plemented enrichment relied on selected fractal at-

tributes, while ensemble models included both deep-

learned and fractal attributes. This lack of equality

in the comparison hindered a deﬁnitive conclusion.

However, the proposed enrichment approach can be

further explored usin g other types of attributes crucial

in the context of H&E im a ges, potentially leading to

new ﬁndings and complementing the results achieved

here.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

474

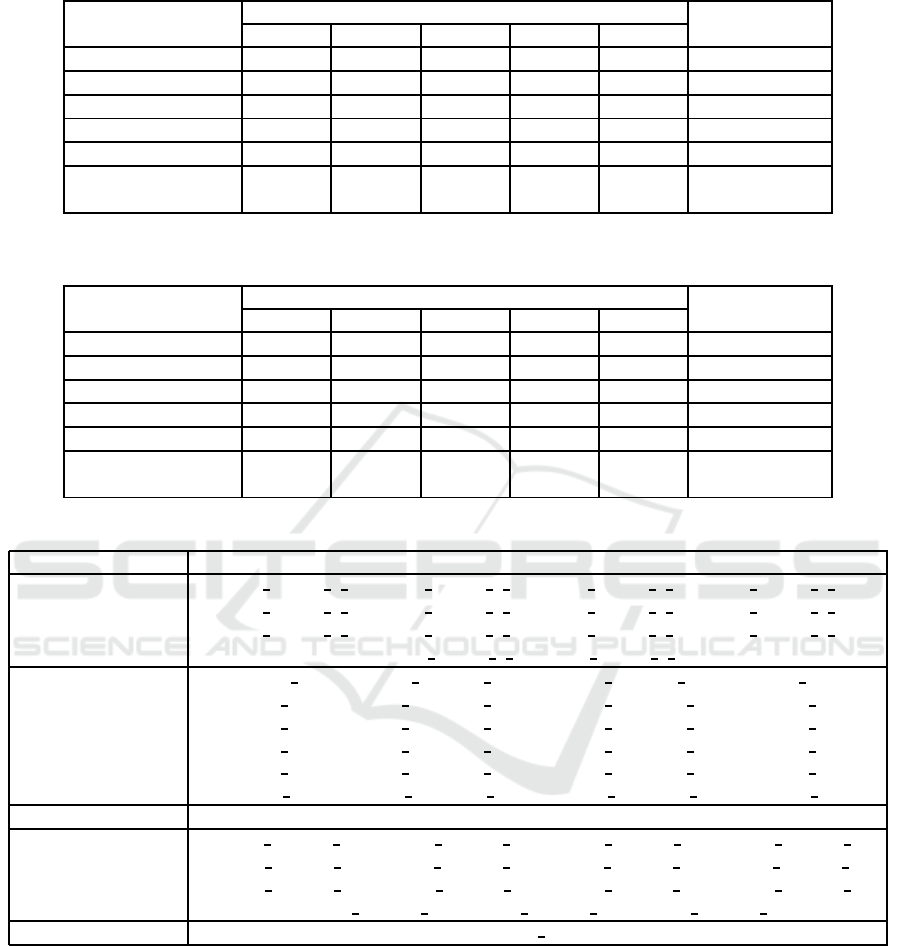
Table 4: Acc rates (%) of enriched models compared to baseline models for various CNN architectures, considering the LG

dataset, min-max normalization and feature incorporation using the vector norm with p = 2.

CNN Architectures

Enriched-CNN (min-max)

baseline model

σ = 1 σ = 3 σ = 5 σ = 10 σ = 20

ResNet50 67.09 83.54 77.64 78.06 80.59 81.44

InceptionV3 56.96 67.51 56.96 76.37 67.93 83.12

DenseNet121 81.86 91.98 89.03 94.09 91.56 80.17

EfﬁcientNetB2 98.73 99.58 98.73 99.58 99.16 78.48

VGG19 95.78 92.40 97.47 95.78 96.20 89.87

Average ±

80.08 ±

0.18

87.00 ±

0.12

83.97 ±

0.17

88.78 ±

0.11

87.09 ±

0.13

82.62 ±

0.04

Table 5: Acc rates (%) of enriched models compared to baseline models for various CNN architectures, considering the UCSB

dataset, z-score normalization and feature incorporation using the vector norm with p = 1.

CNN Architectures

Enriched-CNN (z-score)

baseline model

σ = 1 σ = 3 σ = 5 σ = 10 σ = 20

ResNet50 68.75 79.00 64.58 68.75 79.17 58.33

InceptionV3 60.42 62.50 68.75 60.42 66.67 64.58

DenseNet121 52.08 70.00 68.75 75.00 52.08 66.67

EfﬁcientNetB2 83.33 89.58 89.58 91.67 87.50 75.00

VGG19 85.42 93.75 90.00 89.58 81.25 56.25

Average ±

70.00 ±

0.14

78.33 ±

0.14

76.67 ±

0.13

77.08 ±

0.13

73.33 ±

0.14

64.16 ±

0.07

Table 6: Layers that exhibited the best performance during the enrichment process based on the studied architectures.

CNN Architectures Enriched laye rs indicated by name

ResNet50

conv2 block1 3 bn, conv2 block2 3 bn, conv2 block3 3 bn, conv3 block1 0 bn,

conv3 block1 3 bn, conv3 block2 3 bn, conv3 block3 3 bn, conv3 block4 3 bn,

conv4

block1 0 bn, conv4 block2 3 bn, conv4 block3 3 bn, conv4 block6 3 bn,

conv5 block1 3 bn, conv5 block2 3 bn

InceptionV3

batch norm alization 5, batch normalization 7, batch nor m alization 18,

batch

normalization 21, batch normalization 2 4, batch normalization 26,

batch normalization 33, batch normalization 39, batch normalization 43,

batch

normalization 48, batch normalization 5 8, batch normalization 71,

batch normalization 78, batch normalization 82, batch normalization 83,

batch norm alization 87, batch normalization 88, batch normalization 93

DenseNet121 bn

EfﬁcientNetB2

block1a pro ject bn, block1b pro ject bn, block2a pro ject bn, block2b pro ject bn,

block2c

pro ject bn, block3c pro je ct bn, b lock4a pro ject bn, block4c pro ject bn,

block4d pro ject bn, block5a pro ject bn, block5c pro ject bn, block6a pro ject bn,

block6c

pro ject bn, block6e pro ject bn, block7a pro ject bn

VGG19 block5 conv4

3.1 Comparative Overview

To emphasize the importance of the pro posed method

and its feasibility, the results presented he re were

compare d with those of other established and relevant

studies in this research area. The compar isons are pre-

sented in Table 8 for each H&E histological dataset.

Most studies presented in the table focus on en-

semble descriptor strategies, w here the best results

are generally achieved through combin ations involv-

ing deep-learned attributes. When only handcrafted

attributes or com binations focused on these attributes

are considered, the overall results are not impressive

for most methods. The method proposed in this study

introdu ced a new ap proach for CNN architectures to

leverage handcrafted attributes, maximizing their po-

tential during training. Moreover, this integration was

subtle and did not signiﬁcantly alter the architectures.

This highlights the advantage o f the proposed ap-

proach .

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

475

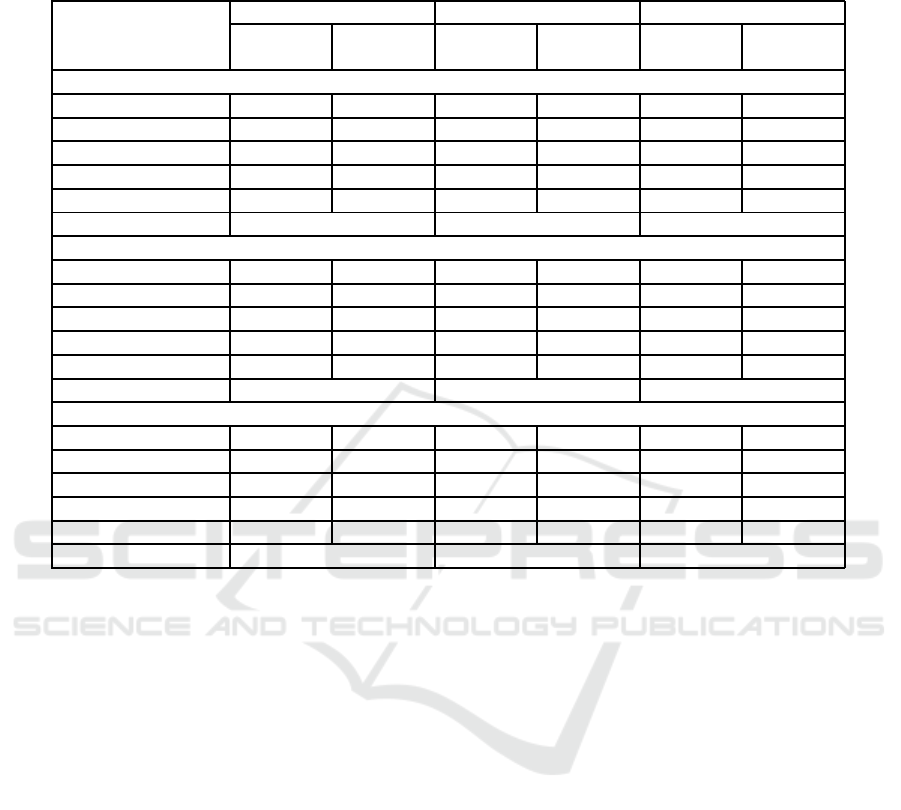
Table 7: Acc rates (%) of enriched models compared to those obtained using fractal attributes applied to machine learning al-

gorithms and to those of models enriched through ensemble descriptor strategies using various CNN architectures, considering

the CR, LG and UCSB datasets.

CNN Architectures

σ = 5 σ = 10 σ = 20

Enriched-

CNN

Ensemble

Enriched-

CNN

Ensemble

Enriched-

CNN

Ensemble

ResNet50 66.67 94.55 81.63 95.15 55.10 97.58

InceptionV3 97.28 95.15 97.96 92.73 97.2 8 97.58

DenseNet121 97.28 95.76 98.64 97.58 97.2 8 99.39

EfﬁcientNetB2 97.28 95.15 100 99.39 97.96 99.39

VGG19 100 95. 15 97.28 96.36 99.32 97.58

Fractal Attributes 80.61 84.24 86.06

ResNet50 77.64 95.85 78.06 98.49 80.59 98.11

InceptionV3 56.96 88.68 76.37 88.30 67.9 3 95.85

DenseNet121 89.03 97.74 94.09 99.25 91.5 6 99.62

EfﬁcientNetB2 98.73 93.96 99.58 94.34 99.16 96.23

VGG19 97.47 92.83 95.78 94.34 96.20 94.34

Fractal Attributes 80.38 90.19 93.96

UCSB

ResNet50 64.58 86.21 68.75 91.38 79.17 91.38

InceptionV3 68.75 81.03 60.42 87.93 66.6 7 87.93

DenseNet121 68.75 86.21 75.00 86.21 52.0 8 91.38

EfﬁcientNetB2 89.58 79.31 91.67 84.48 87.5 0 89.66

VGG19 90.00 74.14 89.58 74.14 81.2 5 86.21

Fractal Attributes 72.41 68.97 74.14

4 CONCLUSIONS

This study developed a novel method for enriching

CNN. In this method, deep-learned features were en-

riched through backpropag a tion using relevant frac-

tal techniques commonly applied in H&E image con-

texts. The results achieved in the studied histolog-

ical datasets in dicate the feasibility of the proposed

method, including ind ications of th e combinations

that contributed the most. It was important to inves-

tigate different selection, normalization and attribute

incorporation strategies in the performance analy sis

of various CNN arc hitectures. The method also high-

lighted how architectures can be enriched without ma-

jor structural changes. This opens the door for ap-

plying the method to other types of architectures be-

sides CNN. Comparison with related studies suggests

that the method achieved notable performance with

just a few fractal attributes, while other studies of-

ten utilized deep-learne d attributes or combinations

with more f eatures. Moreover, the method consis-

tently outperformed traditional training w ith the in-

dicated architectures in most situation s.

This op ens up new possibilities for future re-

search, such as applyin g enrichment to architectures

beyond CNN, as well as exploring other attributes rel-

evant to the investigated context. Investigating forms

of incorporation beyond the loss function c ould also

lead to new interpretations and potentially improve

the classiﬁcation systems developed.

ACKNOWLEDGEMENTS

This research was funded in part by the: Coordenac¸˜ao

de Aperfeic¸oamento de Pessoal de N´ıvel Superior

- Brasil (CAPES) - Finan c e Code 001; National

Council for Scientiﬁc and Technological Develop-

ment CNPq (grants #132940/2019-1, #313643/2021-

0 and #311404/2021-9); the State of Minas Gerais Re-

search Foundation - FAPEMIG (gran t #APQ-00578-

18); S˜ao Paulo Research Foundation - FAPESP (grant

#2022/03020-1).

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

476

Table 8: Acc rates (%) of Enriched-CNN models compared to other t echniques, considering the CR, LG and UCSB dataset.

Method Approac h

Type of

Attributes

Number of

attributes

Acc

Enriched-CNN

VGG19 enriched by a ttributes

L (PERC and LAC) and G (S)

Handcraf ted 5 100

(Longo et al., 2023) DenseNet121 and EfﬁcientNetB2

Ensemble of

deep-lear ned

10 100

(Roberto et al., 2021) ResNet50, D, LAC an d PERC

Ensemble of

deep-lear ned

and hand c rafted

300 99.39

(Dabass et al., 2019) 31-layered CNN Deep-learn ed - 96.97

(Di Ruberto et al., 2016)

Statistical Analysis and

Texture Descriptors

Handcraf ted 20 100

(Longo et al., 2023) DenseNet121 and ResNet50

Ensemble of

deep-lear ned

25 100

(Roberto et al., 2021) ResNet50, D, LAC an d PERC

Ensemble of

deep-lear ned

and hand c rafted

300 99.62

Enriched-CNN

EfﬁcientNetB2 enrich ed by

attributes L (LAC) and G (Γ)

Handcraf ted 3 99.58

(Andrearczyk and Whelan, 2017) Texture CNN Deep-learn ed - 99.10

UCSB

(Yu et al., 2019)

CNN, LBP, SURF, GLCM a nd

others

Ensemble of

deep-lear ned

and hand c rafted

319 96.67

(Longo et al., 2023) DenseNet121 and EfﬁcientNetB2

Ensemble of

deep-lear ned

25 94.83

Enriched-CNN

VGG19 enriched by a ttributes

L (PERC) and G (Γ)

Handcraf ted 3 93.75

(Kausar et al., 2019)

Color normalization, Haar wavelet

decomposition and a 16-laye red

CNN

Deep-learn ed - 91.00

(Roberto et al., 2021) ResNet50, D, LAC an d PERC

Ensemble of

deep-lear ned

and hand c rafted

300 89.66

REFERENCES

Almaraz-Damian, J.-A., Ponomaryov, V., Sadovnychiy, S.,

and Castillejos-Fernandez, H. (2020). Melanoma and

nevus skin l esion classiﬁcation using handcraft and

deep learning feature fusion via mutual information

measures. Entropy, 22(4):484.

Andrearczyk, V. and Whelan, P. F. (2017). Deep learning

for biomedical texture image analysis. In Proceedings

of the Irish Machine Vision & Image Processing Con-

ference. Irish Pattern Recognition & Classiﬁcation So-

ciety (IPRCS).

Cheng, C., Xu, T., and Wu, X.-J. (2023). Mufusion: A

general unsupervised image fusion network based on

memory unit. Information Fusion, 92:80–92.

Dabass, M., Vig, R., and Vashisth, S. (2019). Five-grade

cancer classiﬁcation of colon histology images via

deep learning. In Communication and Computing

Systems: Proceedings of the 2nd International Con-

ference on Communication and Computing Systems

(ICCCS 2018), December 1-2, 2018, Gurgaon, India,

page 18. CRC Press.

de Oliveira, C. I., do Nascimento, M. Z., Roberto, G. F. ,

Tosta, T. A., Martins, A. S., and Neves, L. A. (2023).

Hybrid models for classifying histological images: An

association of deep features by transfer learning with

ensemble classiﬁer. Multimedia Tools and A pplica-

tions, pages 1–24.

Di Ruberto, C., Putzu, L., Arabnia, H., and Quoc-Nam, T.

(2016). A feature learning f r amework for histology

images classiﬁcation. Emerging trends in applications

and infrastructures for computational biology, bioin-

formatics, and systems biology: systems and applica-

tions, pages 37–48.

Convolutional Neural Networks Enriched by Handcrafted Attributes (Enriched-CNN): An Innovative Approach to Pattern Recognition in

Histological Images

477

Diao, S., L uo, W., Hou, J., Lambo, R., Al-Kuhali,

H. A ., Zhao, H., Tian, Y., Xie, Y., Zaki, N., and

Qin, W. (2023). Deep multi-magniﬁcation similar-

ity learning for histopathological image classiﬁcation.

IEEE Journal of Biomedical and Health Informatics,

27(3):1535–1545.

Gelasca, E. D., Byun, J., Obara, B., and Manjunath, B.

(2008). Evaluation and benchmark for biological im-

age segmentation. In 2008 15th IEEE International

Conference on Image Processing, pages 1816–1819.

IEEE.

Hosseini, V. R., Mehrizi, A. A., Gungor, A., and Afrouzi,

H. H. (2023). Application of a physics-informed neu-

ral network to solve the steady-state bratu equation

arising from solid biofuel combustion theory. Fuel,

332:125908.

Hu, Z., Zhang, J., and Ge, Y. (2021). Handling vanishing

gradient problem using artiﬁcial derivative. IEEE Ac-

cess, 9:22371–22377.

Ivanovici, M. and Richard, N. (2009). The lacunarity of

colour fractal images. In Image Processing (I CIP),

2009 16th IEEE International Conference on, pages

453–456. IEEE.

Ivanovici, M. and Richard, N. (2011). Fractal dimension

of color fractal images. IEEE Transactions on Image

Processing, 20(1):227–235.

Jahan, I., Ahmed, M. F., Ali, M. O., and Jang, Y. M. (2022).

Self-gated rectiﬁed linear unit for performance im-

provement of deep neural networks. ICT Express.

Kausar, T., Wang, M., Idrees, M., and Lu, Y. (2019). Hwd-

cnn: Multi-class recognition in breast histopathology

with haar wavelet decomposed image based convolu-

tion neural network. Biocybernetics and Biomedical

Engineering, 39(4):967–982.

Kononenko, I.,

Simec, E., and Robnik-

Sikonja, M. (1997).

Overcoming the myopia of inductive learning algo-

rithms with relieff. Applied Intelligence, 7(1):39–55.

Longo, L. H. d. C. , Roberto, G. F., Tosta, T. A., de Faria,

P. R. , Loyola, A. M., Cardoso, S. V., Silva, A. B.,

do Nascimento, M. Z., and Neves, L. A. (2023). Clas-

siﬁcation of multiple h&e images via an ensemble

computational scheme. Entropy, 26(1):34.

Martinez, E. Z., Louzada-Neto, F., and Pereira, B. d. B.

(2003). A curva roc para testes diagn´osticos. Cad.

sa´ude colet.,(Rio J.), 11(1):7–31.

Montalbo, F. J. P. (2022). Diagnosing gastrointestinal dis-

eases from endoscopy images through a multi-fused

cnn with auxiliary layers, alpha dropouts, and a fu-

sion residual block. Biomedical Signal Processing

and Control, 76:103683.

Nanni, L., Ghidoni, S., Brahnam, S ., Li u, S., and Zhang,

L. (2020). Ensemble of handcrafted and deep learned

features for cervical cell classiﬁcation. I n Nanni, L.,

Brahnam, S., Brattin, R., Ghidoni, S., and Jain, L., ed-

itors, Deep Learners and Deep Learner Descriptors

for Medical A pplications. Intelligent Systems Refer-

ence Library, volume 186, pages 117–135. Springer.

Ponti Jr, M. P. (2011). Combining classiﬁers: from the cre-

ation of ensembles to the decision fusion. In 2011 24th

SIBGRAPI Conference on Graphics, Patterns, and Im-

ages Tutorials, pages 1–10. IEEE.

Rajinikanth, V., Joseph Raj, A., Thanaraj, K., and Naik, G.

(2020). A customized vgg19 network wit h concatena-

tion of deep and handcrafted features for brain tumor

detection. Appl. Sci., 10(10):3429.

Roberto, G. F. , Lumini, A., Neves, L. A., and do Nasci-

mento, M. Z. (2021). Fractal neural network: A new

ensemble of fractal geometry and convolutional neu-

ral networks for the classiﬁcation of histology images.

Expert Systems with Applications, 166:114103.

Roberto, G. F., Neves, L. A., Nascimento, M. Z., Tosta,

T. A., Longo, L. C. , Martins, A. S., and Faria, P. R.

(2017). Features based on the percolation theory for

quantiﬁcation of non-hodgkin lymphomas. Comput-

ers in biology and medicine, 91:135–147.

Sirinukunwattana, K., Pluim, J. P., Chen, H., Qi, X. , Heng,

P.-A., Guo, Y. B., Wang, L. Y., Matuszewski, B. J.,

Bruni, E., Sanchez, U., et al. (2017). Gland segmen-

tation in colon histology images: The glas challenge

contest. Medical i m age analysis, 35:489–502.

Sukegawa, S., Fujimura, A., Taguchi, A., Yamamoto, N.,

Kitamura, A., Goto, R., N akano, K., Takabatake, K.,

Kawai, H., Nagatsuka, H., et al. (2022). Identiﬁcation

of osteoporosis using ensemble deep learning model

with panoramic radiographs and clinical covariates.

Scientiﬁc reports, 12(1):1–10.

Tenguam, J. J., Longo, L. H. d. C., Roberto, G. F., Tosta,

T. A., de Faria, P. R., Loyola, A. M., Cardoso, S. V.,

Silva, A. B., do Nascimento, M. Z. , and Neves, L. A.

(2024). Ensemble learning-based solutions: An ap-

proach for evaluating multiple features in the con-

text of h&e histological images. Applied Sciences,

14(3):1084.

Wu, M., Zhu, C., Yang, J., Cheng, S., Yang, X., Gu, S., Xu,

S., Wu, Y., Shen, W., H uang, S., et al. (2023). Explor-

ing prognostic indicators in the pathological images

of ovarian cancer based on a deep survival network.

Frontiers in Genetics, 13:1069673.

Xu, L., Zhang, H., Song, L., and Lei, Y. (2022). Bi-

mgan: Bidirectional t1-to-t2 mri images prediction us-

ing multi-generative multi-adversarial nets. Biomedi-

cal Signal Processing and Control, 78:103994.

Yu, C., Chen, H., Li, Y., Peng, Y., Li, J., and Yang, F.

(2019). Breast cancer classiﬁcation i n pathological

images based on hybrid features. Multimed Tools

Appl, 78:21325–21345.

Zahn, J. M., Poosala, S., Owen, A. B., Ingram, D. K.,

Lustig, A., Carter, A., Weeraratna, A. T., Taub, D. D.,

Gorospe, M., Mazan-Mamczarz, K., et al. (2007).

Agemap: a gene expression database for aging in

mice. PLoS genetics, 3(11):e201.

Zhang, F., Lin, S., Xiao, X., Wang, Y., and Zhao, Y. (2024).

Global attention network with multiscale feature fu-

sion for infrared small target detection. Optics &

Laser Technology, 168:110012.

Zheng, H., Hu, Z., Yang, L., Xu, A., Zheng, M., Zhang, C.,

and Li, K. (2023). Multi-feature collaborative fusion

network with deep supervision for sar ship classiﬁca-

tion. IEEE Transactions on Geoscience and Remote

Sensing.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

478