Enhancing Student Learning in Tertiary Education Through

Simulation

Nang Laik Ma

, Ivy Sook May Chia

and Murphy Junyu Choy

Singapore University of Social Sciences, Singapore

Singapore Management University, Singapore

Keywords: Simulation, Students’ Learning Activities, Experiential Learning, Learning Analytics, Predict Students’ Score.

Abstract: Simulation-based learning has emerged as a transformative approach to enhancing student learning in tertiary

education, bridging the gap between theoretical knowledge and practical application. Our university has

employed simulation-based learning in an undergraduate course for nearly a decade, training thousands of

students to foster active engagement, critical thinking, and problem-solving skills. The pivot of this approach

is a virtual business simulation where students, organized in teams of five, manage a comprehensive business

over a twelve-week semester. The simulation has multiple departments ranging from forecasting, finance,

operations, transportation, and logistics to give our freshers a holistic overview of how to run a business and

the interdependency and connection between departments. Student activities are continuously tracked during

the simulation. As instructors, we can download the learner activities after the simulation game. It enables us

to develop a predictive model with 90% accuracy in forecasting the students’ final scores. This model supports

timely, pre-emptive interventions to identify students who might need additional assistance and help them

increase their active participation. At the end of the course, each team will give a fifteen-minute presentation

to showcase their simulation results, strategic thinking, and data analysis skills using simulation-generated

data. This paper provides valuable insights into best practices and future directions for leveraging simulations

in tertiary education. It emphasizes the role of simulations in tertiary education, which fosters teamwork,

critical thinking, and real-world business acumen. In addition, the simulation also effectively prepares

students for professional success in a dynamic and competitive landscape.

1 INTRODUCTION

Our business school welcomes students from diverse

academic backgrounds, including those from local

polytechnics and G.C.E. “A” level programs. While

this diversity enriches the educational atmosphere, it

also presents a challenge, as many students begin with

limited knowledge of business concepts. We

incorporated a cloud-based business simulation into

one of our foundational courses to bridge this gap and

provide a comprehensive foundation for the business

program.

The course integrates business modeling with

simulation. The objectives of this simulation are

threefold. Firstly, it enables students to grasp a broad

spectrum of business concepts, explore the

dependency and interconnectivity among various

business functions and departments, and understand

how to operate a business through hands-on

experiential learning. The course emphasizes

problem-solving and self-directed learning,

equipping students with business modeling,

analytical skills, and a resilient mindset to thrive in

complex, real-world scenarios.

Since early 2015, we have integrated

MonsoonSIM, an innovative and unique pedagogical

experiential learning platform, into our business

curriculum. The platform immerses students in the

complexities of managing a business, covering more

than ten interconnected departments, such as retail,

wholesale, e-commerce, production, finance, HR, and

others. The students learn complex business

operations and the fundamentals through an

interactive and highly competitive game setting.

Since there are more than ten departments with a

maximum of five students in a team, each student

needs to take charge of more than one department.

Good communication skills and collaborative efforts

are the byproduct of a successful simulation game.

Additionally, the first simulation games act as an ice-

Ma, N. L., Chia, I. S. M. and Choy, M. J.

Enhancing Student Learning in Tertiar y Education Through Simulation.

DOI: 10.5220/0013278300003932

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 2, pages 705-712

ISBN: 978-989-758-746-7; ISSN: 2184-5026

705

breaker among the team members to get to know each

other by having the same common goal of running a

company successfully. Over the years, students have

consistently given us feedback on the positive impact

of the simulation game as an invaluable tool,

enhancing their learning and ability to explore the

multifaceted business world.

The contribution of this paper is twofold. First, we

aim to share our experience designing and

implementing a course incorporating simulation-

based learning into our business program curriculum.

We include a detailed overview of the pedagogical

framework, the integration of MonsoonSIM as the

simulation tool, and the assessment methodology

developed to evaluate student performance

effectively. The second objective of this paper is to

create a predictive model to forecast the students'

final score by leveraging the learner activities during

the simulation game in the first week. This model is

an early detector to identify at-risk students with low

engagement and participation, enabling timely

intervention to support their academic journey. With

the advancement of technology, students today are

leaving enormous amounts of digital traces online,

such as login details, online learning platforms, and

social media websites. By monitoring student

performance through data-driven insights, we aim to

optimize learning outcomes, foster personalized

learning approaches, and improve overall academic

success.

2 LITERATURE REVIEW

Granlund et al. (2000) designed a web-based

simulation for learning. Using the C3Fire simulation,

the authors highlighted how the four stages of the

experiential learning cycle (concrete experience,

reflective observation, abstract conceptualization,

and active experimentation) helped students develop

evaluation skills in a group educational setting. Desai

et al. (2018) tested the efficacy of Project-Based

Learning (PBL), an experiential learning approach,

by comparing students' academic performance in two

colleges. One group used PBL to solve real-world

problems, while the other followed traditional

lecture-based methods. The results of T-tests revealed

a significant improvement in students' performance in

Semester End Exams (SEE) and placements in the

PBL group. It showed that experiential learning

benefits students in the light of creativity and

innovation, and problem-solving skills are needed for

excellent academic performance.

Several studies have leveraged learning

management system (LMS) data in educational data

analytics to improve student achievement. Aldowah,

Al-Samarraie, Wan Mohamad (2019), and Chiappe

and Rodriguez (2017) have utilized LMS data to

identify patterns that can inform interventions to

improve student performance.

Ma and Chia (2020) developed a learning

analytics course centered around PBL, focusing on

solving real-world problems. The course received

positive student feedback, and a follow-up study by

Ma and Chia (2023) demonstrated how predictive

models—such as decision trees, regression, and

neural networks—could be used to predict student's

cumulative grade point averages (CGPA) based on

course performance. The regression model yields the

lowest mean absolute error (MAE), suggesting its

effectiveness in predicting the students' CGPA.

Based on the literature review, a notable gap

emerges in using simulation-based learning to predict

students' academic performance. Several authors

have demonstrated the positive outcomes of

simulation as it enhances students' engagement and

improves their problem-solving ability. However,

few have explored using the data generated through

simulation activities to predict students' academic

performance.

In the subsequent sections of this paper, we

explore pedagogical frameworks designed to

integrate simulations into our course successfully. We

outline how simulations can be integrated and

structured to support experiential learning and data

collection for predictive analysis. In section four, we

focus on how the learner activities, such as student

interactions within the simulation game, can serve as

meaningful data points to predict students' final

scores. We explained the development of regression

models and shared some actionable insights.

3 PEDAGOGICAL

FRAMEWORKS

In this section, we focus on the pedagogical

framework with the underlying teaching philosophy,

teaching methods, and assessment methods to ensure

the proper delivery of the course. We focus on the

student's learning process, ensuring students have a

high engagement level with the course materials and

a comprehensive understanding of business

functions. At the beginning of the course,

simulation-based learning forms a core component,

with MonsoonSIM providing a cloud-based dynamic

CSEDU 2025 - 17th International Conference on Computer Supported Education

706

platform allowing students to play the game onsite or

remotely at their convenience. Students are excited

about playing the simulation game, where students

immerse themselves in interactive scenarios that

mimic real-world business operations. This hands-on

experience allows students to apply theoretical

knowledge to practical situations, enhancing their

action-planning and strategic thinking abilities.

This compulsory course for all undergraduate

business students aims to provide a comprehensive

understanding of core business functions and their

interrelationships within an organization. Through a

combination of experiential learning techniques—

such as business simulation games, industry-driven

case studies, and spreadsheet-based analysis—

students will develop critical skills in problem

identification, decision-making, and business

modeling.

3.1 Learning Objectives

The course is designed with six learning outcomes in

mind:

• Formulate business problems using Spreadsheet

techniques

• Apply data analysis skills for better decision-

making

• Identify business strategies to deal with changes.

• Provide students with a holistic understanding of

business operations and decision-making.

• Encourage collaboration and teamwork through

group-based tasks.

• Foster critical thinking and problem-solving

skills through simulation.

3.2 Experiential Learning Approach

The framework emphasizes experiential learning,

where students “learn by doing” in the MonsoonSIM

simulation game. At the outset of the course, each

lecturer will randomly assign all the students to a

team of at most five at the beginning of the first

seminar. Each team will manage a business selling

products at retail, e-commerce, and wholesale to be

financially substantial, with the highest revenues and

profit at the end of the game. In a regular class, about

40 students forming eight teams will compete and be

ranked based on some key financial indicators.

Students are encouraged to watch the video on how

to play the game before the lesson. During the

session, the instructor dedicates approximately one

hour to explaining the key functions of the virtual

business environment. The lecturer will also show a

demo of running the simulation game live, briefly

touching most of the functions. Before we started the

game, lecturers gave students fifteen minutes for

discussion. During the discussion, students identify

their tasks and job roles in the game based on their

prior knowledge of departments and experiences.

Most students felt lost as it differed from most of the

mobile phone games they had played. The setting for

the actual game lasts for an hour, at least 75 simulated

days, and each day will last about 45 seconds to

minutes. It is an extensive, competitive, and

interactive session where students actively manage a

virtual business entity, navigating and coordinating

the operations of various interdependent departments.

The departments in the simulations are B2B or

Wholesale, Customer Service, E-commerce, Finance

and Accounting, Human Resources, Logistics and

Warehouse, Maintenance, Marketing, MRP,

Forecasting and Planning, Procurement, Production,

and Retail.

During the simulation activities, detailed records

of learner activities are maintained, providing

valuable data for the authors to develop a predictive

model. The simulation generates extensive

transactional, operational, and financial data, which

students can analyze after the game, using their data

analysis and problem-solving skills. By interpreting

these data, students formulate new business strategies

to improve key performance indicators such as profit

and loss, production efficiency, and inventory

turnover ratios in the subsequent games.

Over the twelve-week semester, students engage

in multiple offsite simulation games, learning through

hands-on experience. Experiential learning allows

students to explore many business functions under

various scenarios and diverse business strategies.

Through iterative gameplay, they refine their

approaches, leveraging the insights gained from data

analysis to optimize outcomes. While students may

initially possess limited knowledge of business

operations, the experiential learning process enables

them to develop a deep understanding of the roles and

interdependencies of various business departments.

3.3 Self-Directed Learning Approach

More than 70% of our university's students are

working adults. Thus, their time at the university is

limited. They want more emphasis on autonomy and

independence. We upload all the teaching materials,

including the study guide and e-textbook, which are

available to all enrolled students six weeks before the

start of the course. Attendance is strongly

encouraged, but if the students cannot attend the class

physically due to overseas work travel or

Enhancing Student Learning in Tertiary Education Through Simulation

707

commitment, there will be a means for them to

continue learning. We provide a video recording of

each semester, and students can self-learn by

referring to these resources at their own pace and in

their flexible time. We design pre-class quizzes to

encourage students to self-learn and complete them

online before class to promote knowledge acquisition.

With the new technological advancement in learning

management systems (LMS), we encourage students

to develop self-directed learning and lifelong learning

habits.

3.4 Assessment Methods Overview

Our assessment method comprises several

components designed to comprehensively evaluate

students' understanding and application of course

material. Here is the breakdown of each assessment

component and its weight in the overall grade:

i. Pre-Class Quizzes (20%)

We administer four pre-class quizzes to actively

motivate students to study the material before

each lesson to evaluate their foundational

understanding of essential concepts. Pre-class

quizzes are part of the self-directed learning

approach and equip students with meaningful

participation in the upcoming class discussion.

The pre-class quizzes are multiple choice

questions (MCQ) and have twenty questions for

each. Students can complete it within a week

before the deadline. These quizzes account for

20% of the overall grade, which is critical in

promoting proactive and consistent learning.

ii. Individual Assignment on Business

Modeling (30%)

A substantial assessment component focuses on

an individual assignment involving business

modeling using spreadsheet tools. This

assignment also includes a reflective question

based on the outcomes of a simulation game.

Typically, students excel in this assignment,

demonstrating strong performance on this task

and underscoring the importance of the learning

process. This assignment contributed 30% of

their overall grade. The assignment paper is

published online at the start of the course, giving

students four weeks to complete it

independently. This extra timeline promotes

comprehensive research and a thorough

understanding of the course material.

iii. Simulation Games and Final

Presentation (20%)

Students actively engage in multiple simulation

game sessions throughout the course to improve

their scores and ranking. Students' performance

in the simulation is assessed through a

comprehensive scoring matrix, which calculates

a weighted average of multiple key performance

metrics. The scoring matrix includes crucial

financial indicators such as profit or loss, cash on

hand, the customer satisfaction index from B2B

and e-commerce, and the staff turnover ratio.

These factors play a significant role in evaluating

overall performance, reflecting the various

aspects of a business's success. Instructors can

select from a diverse range of over 30

combinations of key performance indicators

(KPIs) tailored to different learning objectives

and scenarios. This flexibility allows educators

to create a customized assessment framework

that aligns with the course goals and the specific

skills they wish to evaluate. We finalized the

scoring matrix at the beginning of the course. We

shared it with the students at the first game,

ensuring it was firmly established and consistent

throughout all simulation games. Consistency is

essential for accurately measuring and

comparing students' performance across

different rounds, as it helps to eliminate

variability that could arise from changing

evaluation criteria. By maintaining a stable

scoring matrix, we can provide students with

precise and reliable performance feedback,

enhancing their learning experience and helping

them improve their business acumen.

In week twelve, these game sessions culminate in

a group presentation where students articulate

their findings and strategic approaches

developed during the simulations. The

assessment of this presentation is guided by a

detailed rubric evaluating key dimensions,

including the quality of presentation delivery, the

rigor of strategic application within the

simulation, the depth and precision of data

analysis, and the significance of the learning

outcomes derived from the experience. The

activity constitutes 20% of the overall course

assessment, emphasizing its vital role in

developing collaborative learning, critical

thinking, effective communication, and

teamwork.

CSEDU 2025 - 17th International Conference on Computer Supported Education

708

iv. Final Examination (30%)

The course concludes with an open-book

examination to assess students' comprehensive

understanding of the course content. Students

can use the Internet, wifi, and laptops during the

two-hour exams, which feature two business-

focused questions. These questions require the

development of spreadsheet models to solve

complex, real-world problems, emphasizing the

practical application of course concepts. The

final examination accounts for 30% of the total

assessment, one of the highest weights for the

course assessment, similar to the assignment.

Even though we encourage collation, at least

80% of the course assessment is based on the

individual work effort. Setting the exam paper is

quite a challenge for the instructors. It is required

to meet at least 60% of the learning outcome and

to ensure students can integrate and apply

knowledge effectively in a structured, problem-

solving context.

Typically, students find it challenging to excel in

this final examination component. The difficulty

arises because the problems presented are often

unforeseen, requiring students to state their

assumptions, work with unknowns, employ critical

thinking, and adapt swiftly. Moreover, they face the

added pressure of completing the exam within a strict

two-hour time limit, which can exacerbate feelings of

anxiety and hinder their ability to perform at their

best. Even with the extensive online resources, such

as study guides, eTextbooks, educational websites,

and AI tools designed to assist with problem-solving,

many students still struggle to achieve satisfactory

results in this exam. This act of moderation enables

the educator to accurately assess students' ability to

apply their skills to real-world, unfamiliar problems,

genuinely reflecting their proficiency.

4 PREDICTIVE MODELING

WITH REGRESSION

When students engage in the simulation game, the

platform meticulously tracks their activities by

recording the number of transactions they perform

during gameplay. Data collection is essential for

analyzing how students interact with the game and

can provide insights into their learning processes.

After the first match, the instructors can download

all relevant data from the website, facilitating further

analysis and review. We want to build a predictive

model to use the data from the first week to predict

the students' final course scores. The predictive model

will help us identify students with low scores so we

can engage those at-risk students early to improve

their engagement and final academic achievement.

To maintain confidentiality and protect students'

identities, we have taken measures to mask

identifiable information and have assigned new

student IDs exclusively for this analysis. The new

student IDs are the primary key to the data analysis.

We collected nearly a hundred student records from

the most recent three semesters participating in the

simulation games. Table 1 shows the data structure of

the student data.

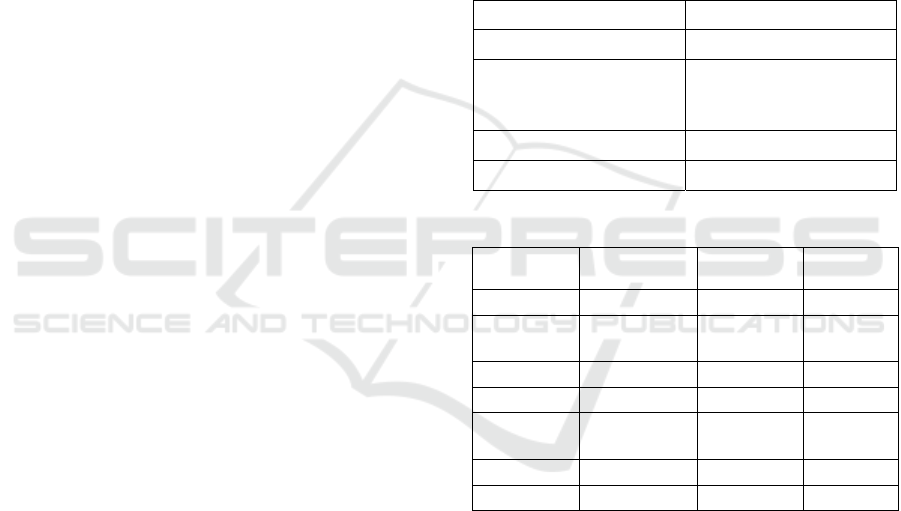
Table 1: Student data.

Description Data Field

Student ID Categorical

Learner activity count

(X1)

The number of activities

done by students in the

first game.

Pre-class quiz score (X2) First Quiz score (0 - 100)

Final score (Target: Y) Final score (0 - 100)

Table 2: Summary statistics of students’ data.

Learner

activity count

Pre-class

quiz score

Final

score

Mean 23.21 81.41 71.19

Standard

Error 1.94 1.64 0.85

Median 19. 85 72.13

Mode 20 90 75.10

Standard

Deviation 19.05 16.09 8.34

Minimum 0 0 45.1

Maximum 85 100 88.9

Next, we will explore the descriptive statistics of

the

input variables to gain insights into student

performance and engagement, as shown in Table 2.

The activity count recorded during the simulation

game is 23.2, with a standard deviation of 19. The

significant standard deviation indicates considerable

variability in students' activity levels, suggesting that

some students were highly engaged while others had

limited interaction with the game. The activity counts

range from a minimum of zero to a maximum of 85,

highlighting the diverse engagement experiences

among participants. As educators, we can identify

students whose learner activity count is less than ten

for a consultation session. Based on the author's

experience, students who are inactive in the game are

Enhancing Student Learning in Tertiary Education Through Simulation

709

struggling to keep up with the game's dynamics and

feel at a loss. They cannot contribute and continue the

game as other team members progress. They feel peer

pressure and cannot perform due to their lack of skills

and knowledge. Thus, setting up additional games to

practice with the Robot (BOT) before the next game

will help them gain more confidence and enhance

their contribution and participation in future games.

Regarding academic performance, the mean pre-

class quiz score is 81.4, which can be categorized as

relatively high, which indicates that students

generally entered the course with a good

understanding of the material since the course

materials are available to them six weeks before the

commencement of the course in the online learning

portal. The average final score for the course is 71.2,

with a mode of 75.1, suggesting that while many

students performed around this score, there was also

a spread in individual performances. The standard

deviation for the final scores is 8.34, reflecting some

variation in how students perform in the course.

Next, the authors will develop the regression

predictive model to predict the student's final score

(Y) using two input variables: learners' activities in

the first simulation game (X1) and the first pre-class

quiz (X2). Regression is a statistical model that finds

the relationship between the independent variable Y

and one or more dependent or explanatory variables

X. The method assumes a linear relationship between

the dependent variables (X)'s and the independent

variable (Y). In this context:

Let i represent a student, where i = 1, 2, …, N.

Let 𝑌



denote the final score of student i.

Let 𝑋1



represent the learner activity count of student

Let 𝑌





be the predicted final score of student i.

Model 1 is a regression model that predicts the final

score 𝑌





solely based on the learner activity count

(X1). Using the regression analysis, the linear

equation derived is:

𝑌



= 0.0177 X1 + 70.78 (1)

We can use equation (1) to compute the predicted

final score for any student. For example, if a student's

activity count (X1) is 60, the predicted score (𝑌



) can

be calculated as:

𝑌



= 0.0177 * 60 + 70.78 = 71.84 (2)

We compare the predicted score ( 𝑌



) to the actual

final score (Y) to evaluate the model. Suppose the

actual score (Y) for this student is 75. The absolute

percentage error (APE) is computed as:

APE =







* 100% =

 .



* 100% = 4% (3)

We use the Mean Absolute Percentage Error (MAPE)

to measure the overall accuracy of the model, which

is calculated for all students:

MAPE =

∑























* 100% (4)

This metric summarizes the model's predictive

accuracy as a percentage error. Using the formula for

absolute percentage error, we can calculate the error

for each student and then determine the average

absolute percentage error to evaluate the model's

accuracy. Model 1 achieves a Mean Absolute

Percentage Error (MAPE) of 8.47%, indicating that

students' activity counts can reasonably predict their

final scores. However, the model has a significant

limitation.

The activity count (X1) ranges from 0 to 85, and

based on the regression equation, 𝑌



= 0.0177 X1 +

70.78, the minimum predicted score for students with

no recorded activity (X1 = 0) is 70.78, corresponding

to the y-intercept. The prediction is problematic

because it assumes that students with no activity will

score at least 70.78. Historical data shows that

approximately 30% of students score below 70,

contradicting this assumption. Additional

explanatory variables must be incorporated to address

this issue and improve the model's accuracy. These

variables could capture other aspects of student

behavior, engagement, or external factors influencing

performance. By incorporating more predictors, we

aim to develop a more comprehensive model that

aligns better with the observed distribution of scores

and accounts for students scoring below the current

minimum prediction.

To address Model 1's limitations and expand its

predictive capability, we introduce an additional

variable: the score from the pre-class quiz conducted

during the first lesson. The first quiz is administered

alongside simulation games in the same week,

offering an early indicator of students' understanding

and engagement with the course content. We intend

to incorporate the pre-class quiz score into model 1

and aim to provide a more accurate prediction of final

scores. If this variable proves to be a significant

predictor, it will allow us to identify students at risk

who are underperforming early in the course.

CSEDU 2025 - 17th International Conference on Computer Supported Education

710

Let 𝑤



,𝑤



, represent the weights assigned to learner

activity count and pre-class quiz score.

Let 𝑊



be the weighted score of student i.

Let 𝑋1



represent the learner activity count of student

Let 𝑋2



represent the pre-class quiz score of student

Let 𝑌





represent the predicted final score of student i.

Model 2 uses the weighted score derived from the

learner activity and pre-class quiz. In this model, 𝑌



represents the predicted final score based on the

combined contributions of X1 and X2, weighted by

the coefficients 𝑤



and 𝑤



We initially assign equal weightage to the learner

activity count and the pre-class quiz score, each

contributing 50% to the weighted score. The score for

each student i is calculated as follows:

𝑊



=𝑤



∗ 𝑋1



+ 𝑤



∗𝑋2



(5)

where 𝑤



=0.5 and 𝑤



=0.5.

The general regression line to predict the student's

score is: 𝑌



= intercept + (slope * weighted score ).

Using regression analysis, we derive the linear

equation:

𝑌



= 59.33 + 0.2267 W (6)

Using the above formula, we compute the absolute

percentage error for each student and calculate the

average to obtain the Mean Absolute Percentage

Error (MAPE) given in equation (4).

Model 2 achieves a MAPE of 7.96%, demonstrating

that combining the learner activity count and the pre-

class quiz score as predictors reduces the error

compared to using a single variable. This indicates

that the two variables provide a more accurate final

score prediction. Next, we aim to determine the

optimal weightage for the two components

( 𝑤



𝑎𝑛𝑑 𝑤



) that minimizes the MAPE. The

optimization is subject to the following constraint:

𝑤



+ 𝑤



=1 (7)

Equation (7) ensures that the total weight sum

equals 1. We can identify the weight distribution that

yields the lowest error by systematically adjusting

𝑤



and 𝑤



while recalculating the MAPE for each

combination. For example, 𝑤



could range from 0 to

1 in increments, with 𝑤



=1− 𝑤



The weighted score 𝑊



and the corresponding

MAPE is computed for each pair. This optimization

process would allow us to assign the most balanced

and optimal weightage between the learner activity

count and the pre-class quiz score, improving the

model's predictive performance.

Using the Excel solver tool, we identify the

optimal weight distribution for the two predictors,

assigning 30% weight ( 𝑤



=0.3) to the learner

activity and 70% weight (𝑤



=0.7) to the pre-class

quiz. Figure 1 produces the minimum MAPE of

7.80%, demonstrating a better predictive model than

other weight combinations. This regression model is

suitable for predicting the students' final scores with

over 90% accuracy.

Figure 1: Varying weightage for the learner activity count

and MAPE.

In conclusion, applying the optimal weight

distribution to the predictive model offers educators a

valuable tool for identifying academically at-risk

students (those with predicted final scores of less than

60) who lack commitment to the course. Using this

early detection, the model allows educators to make

timely interventions, such as providing additional

coaching, mentoring, and tailored additional support

to help students strengthen their ability to learn and

cope with the difficulties they face.

The active approach improves their academic

performance and minimizes the likelihood of course

failure, reducing the risk of attrition in their first

semester. Ultimately, the predictive model serves as

a critical resource for fostering student success and

reducing long-term attrition rates at the university.

5 CONCLUSIONS

In this paper, the authors explore simulation tools in

a tertiary education business program, highlighting

7.93%

7.86%

7.80%

7.85%

7.96%

8.09%

8.22%

8.35%

8.43%

7.70%

7.80%

7.90%

8.00%

8.10%

8.20%

8.30%

8.40%

8.50%

0% 50% 100%

Varying weight w1 verse MAPE

Enhancing Student Learning in Tertiary Education Through Simulation

711

their effectiveness in enhancing student engagement

and promoting experiential learning. By developing a

core business module, the authors share their

pedagogical framework and assessment methods,

providing valuable insights for educators considering

similar course designs. The instructors also face

challenges, such as scheduling simulation games after

office hours and the dynamic nature of the gaming

environment, which sometimes leave students feeling

demotivated when strategies fail.

Incorporating predictive analytics into the

pedagogical framework further amplified its impact

by enabling early identification of at-risk students. By

leveraging data from simulation activities and pre-

class quizzes, predictive models accurately forecasted

student performance and facilitated timely

interventions. These actionable insights improved

academic outcomes and underscored the importance

of analytics-based decision-making in education.

Future research could explore a more profound

integration of simulations with other teaching

methodologies to maximize their impact. With these

advancements, simulation-based learning can evolve

as a transformative educational tool, preparing

students for success in an increasingly dynamic

professional landscape.

REFERENCES

Aldowah, H, Al-Samarraie, H. and Wan Mohamad, F,

(2019). Educational data mining and learning analytics

for 21st century higher education: A review and

synthesis. Telematics and Informatics, 3, 13-49.

Chiappe, A., & Rodríguez, L. P. (2017). Learning Analytics

in 21st-century education: A review. Ensaio: Avaliação

e Políticas PúblicasemEducação, (AHEAD).

Granlund, Berglund and Eriksson (2000). Designing web-

based simulation for learning. Future Generation

Computer Systems, 17, 171-185.

Ma Nang Laik, Ivy Chia (2020). Designing Learning

Analytics for Effective Learning Through Problem-

Based Learning. Journal of Education and Practice,

11(18),27-33. DOI: 10.7176/JEP/11-18-03.

Ma Nang Laik, Ivy Chia (2023). Using education analytics

to predict at-risk students in the university: Case study.

Conference Proceedings of Decision Science Institutes

2023, USA Atlanta.

P. Desai, A. Bhandiwad and A. S. Shettar. (2018). Impact

of Experiential Learning on Students' Success in

Undergraduate Engineering. IEEE 18th International

Conference on Advanced Learning Technologies

(ICALT), Mumbai, India, 2018, 46-50.

Reynol Junco, Candrianna Clem (2015). Predicting course

outcomes with digital textbook usage data. The Internet

and Higher Education.

CSEDU 2025 - 17th International Conference on Computer Supported Education

712