A Study on Different Spectra in Fault Localization

ıcolas Hamparsomian

and Marcos Lordello Chaim

School of Arts, Sciences and Humanities, University of Sao Paulo, Avenue Arlindo B

ettio, 1000, Sao Paulo, Brazil

Keywords:

Fault Localization, Machine Learning, Spectrum, Control Flow, Data Flow, Experimentation.

Abstract:

We present an experimental study to assess the impact of different spectra in fault localization. We evalu-

ated one machine learning-based technique (Deep Neural Networks—DNN) and two Spectrum-based fault

localization (Ochiai and Tarantula). These techniques were applied on 319 faulty versions of industry-like

programs with real bugs using control (statements) and data (deﬁnition use associations—DUA) ﬂow cover-

age as spectra. The results suggest that DNN does not beneﬁt from data ﬂow spectra and any spectrum will

generate similar results using either Ochiai or Tarantula. Among the techniques and spectra assessed, Ochiai

using control ﬂow seems to be the best choice for fault localization.

1 INTRODUCTION

Debugging is characterized as the task of locating and

correcting bugs in programs. It is generally carried

out with the help of static information, such as source

code and execution reports, as well as dynamic infor-

mation, such as the state of variables at runtime, ob-

tained through print commands (e.g., print) or sym-

bolic debuggers (de Souza et al., 2016).

According to a systematic mapping carried out

by Zakari et al. (2018), the most popular technique

within this research ﬁeld is Spectrum-Based Fault Lo-

calization (SBFL), being used in 41% of the studies

surveyed by the mapping. A program’s spectra refers

to trace data generated from the execution of the pro-

gram by a set of tests. SBFL techniques use spectrum

data to suggest components (lines, methods, classes)

most suspicious of being the site hosting a fault caus-

ing an observed failure.

On the other hand, machine learning and data min-

ing techniques have been adopted to facilitate the fault

localization task. Wong and Qi (2011) use backprop-

agation (BP) neural network, statement coverage, and

the output (success or fail) of the tests to highlight the

most suspicious lines hosting a particular bug.

Recent works extend the use of deep learning

models in fault localization (Zhang et al., 2021;

Ghosh et al., 2022; Dutta, 2022; Yan et al., 2022; Qian

et al., 2023). Such a group of techniques establish

https://orcid.org/0009-0007-9524-070X

https://orcid.org/0000-0001-7157-5141

what is called Machine Learning-Based Fault Local-

ization (MBFL).

Fault localization techniques make use of cover-

age data (e.g., statements, branches, deﬁnition use

associations–DUA) (Rapps and Weyuker, 1985) as

spectra to lead the developer towards the most sus-

picious locations of the program under debugging.

However, statement coverage

is the most used spec-

trum for fault localization. The reason for this state

of affairs is because tools that collect line coverage

are available and are performative (e.g., JaCoCo

Notwithstanding, there are works that use data ﬂow

spectra in fault localization (Santelices et al., 2009;

Masri, 2010; Ribeiro et al., 2019).

This paper’s goal is to investigate how DUA and

line coverage perform when used as spectra support-

ing MBFL and SBFL. We conducted a study in which

one MBFL technique (Deep Neural Network–DNN)

and two SBFL techniques (Ochiai and Tarantula)

were applied to locate bugs occurring in 319 faulty

versions of the Defects4J benchmark (Just et al.,

2014).

The organization of the paper is as follows. Ba-

sic concepts and the experimental assessment are pre-

sented, respectively, in Sections 2 and 3. We present

the results in Section 4 and discuss them in Section 5.

Related work and the conclusions and future work are

discussed, respectively, in Sections 6 and 7.

Despite the differences between the terms line, node

and statement, we will interchangeably use them meaning a

set of statements executed sequentially.

https://www.eclemma.org/jacoco/

492

Hamparsomian, N. and Chaim, M. L.

A Study on Different Spectra in Fault Localization.

DOI: 10.5220/0013278500003928

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2025), pages 492-499

ISBN: 978-989-758-742-9; ISSN: 2184-4895

2 BACKGROUND

We discuss brieﬂy below two SBFL techniques—

Tarantula (Jones et al., 2002) and Ochiai (Abreu

et al., 2007)—and one MBFL technique—Deep Neu-

ral Network (Zheng et al., 2016)—because they will

be utilized in our experimental assessment.

2.1 Tarantula and Ochiai

Techniques that use association metrics to rank spec-

tra to pinpoint faulty program components (lines,

branches, DUAs, methods, classes) are referred to in

this paper as SBFL techniques. These metrics are cal-

culated using coefﬁcients that inform how many times

components were, or were not, executed by tests that

pass or fail. The more a component is executed by

tests that fail, the greater the likelihood of hosting a

defect. On the other hand, the less a component is

executed by failing tests, the lower its probability of

hosting a bug. Thus, the chances of a component be-

ing considered suspect are greater when it is often ex-

ecuted by tests that fail and rarely executed by passing

tests.

Tarantula is one of the ﬁrst techniques that utilize

association metrics to rank spectra to locate faults. On

the other hand, Ochiai is one of the most effective as-

sociation metrics (Pearson et al., 2017). We refer the

reader to the work of de Souza et al. (2016) for the

details of how Tarantula and Ochiai rankings are cal-

culated.

2.2 Deep Neural Network

We choose a Deep Neural Network (DNN) model as

a machine learning-based fault localization technique

in our empirical assessment. DNN models are feed-

forward artiﬁcial neural networks containing multiple

hidden layers, which is a model capable of estimat-

ing the complex non-linear relationships between in-

put and output data. Generally, a DNN model can

be used for regression or classiﬁcation tasks; in this

work, it is used as a classiﬁcation model. However, in

order to generate the suspicious values for each code

element, the value produced by the output layer was

not normalized.

Test case execution spectra and their respective re-

sults are are provided as input for training and testing

the model. After training, the suspicious rates of the

the program elements are calculated for comparison

with other fault localization techniques.

3 EXPERIMENTAL

ASSESSMENT

This work implements a deep learning model (DNN)

as a fault localization (FL) technique trained with con-

trol and data ﬂow spectra. The goal is to conduct

an empirical evaluation of the rankings produced by

DNN and SBFL techniques (Tarantula and Ochiai)

obtained with different spectra. The number of source

code components to investigate before locating the

defect is the main measure of comparison.

In what follows, we discuss the research ques-

tions, the deep learning model utilized, the selected

faulty programs, the data collection, and how the lo-

cation of faults was determined. The following exper-

imental design and assessment is similar to that de-

veloped by Pearson et al. (2017).

3.1 Research Questions

The main research question investigated by this work

is described next:

Do MBFL and SBFL techniques perform bet-

ter using data ﬂow or control ﬂow spectra?

To answer this main question, we deﬁned the fol-

lowing research sub-questions:

RQ1: Which spectrum produces better rankings for

DNN?

This question aims to identify, for any given

buggy version of a program, which spectrum op-

timize the accuracy of the DNN model used to lo-

cate faults. We applied a set of comparison met-

rics to assess the spectra ability to locate faults

RQ2: Which spectrum produces better rankings for

Tarantula and Ochiai?

The goal of this research question is to identify,

for a given faulty version of a program, the spec-

trum that better position the bug in the ranking for

SBFL techniques.

RQ3: Which pair (FL technique, spectrum) achieves

the best performance in locating faults?

We also explore the combination of FL technique

(SBFL or MBFL) and spectrum (control or data

ﬂow) to identify the best approach for fault local-

ization.

3.2 Deep Learning Model

The machine learning technique utilized for fault lo-

calization in our experiment is the DNN described in

Section 1. The strategies adopted for modeling the

A Study on Different Spectra in Fault Localization

493

DNN and choosing its hyper-parameters will be pre-

sented next. The DNN presented in this work was de-

veloped based on the guidelines provided in (Zheng

et al., 2016; Zhuo et al., 2017).

3.2.1 Modeling the Hidden Layers

After exploratory experiments, we concluded that a

ﬁxed value of three hidden layers obtained the best

results for the programs present in the Defects4J

database. We caution the reader, though, that the

the number of layers can be deﬁned using pretrain-

ing methods to ﬁne-tune the parameters of the model

(Zheng et al., 2016). However, these dynamic strate-

gies would beneﬁt both control and data ﬂow spectra

and should not impact the comparison of spectra.

3.2.2 Number of Neurons per Layer

The number of neurons of the input and output layers

can be deﬁned directly based on the characteristics of

the data provided for training. The number of neurons

in the input layer is equal to the total number of exe-

cutable elements covered (according to the respective

spectrum) by the tests. The output layer is composed

of a single neuron that represents the result of the test

case execution (success or failure).

For the model presented in this work, we a

adopted the strategy presented in Zhuo et al. (2017)

in which the number of neurons in each hidden

layer is deﬁned according to the following formula:

quantity = round(n/30 + 1) ∗ 10, where n represents

the number of neurons of the previous layer.

3.2.3 Activation Functions Modeling

We chose to follow the guidelines provided in Zhuo

et al. (2017), in which the model used the func-

tion relu to activate the hidden layers and the non-

linear activation function sigmoid for the result gen-

erated in the output layer. Such a parameterization

showed the best results during the experimentation

carried out for our model. The formulas applied by

each of the functions are: relu(x) = max(0,x) and

sigmoid(x) = 1/(1 +e

−x

), where x represents the out-

put vector of the previous layer that will be trans-

formed based on the respective activation function de-

ﬁned for each layer.

3.2.4 Learning Rate Modeling

Zheng et al. (2016) chose manually the learning rate

through experimentation for each of the programs ex-

plored. On other hand, Zhuo et al. (2017) adopted the

strategy to dynamically deﬁne the learning rate start-

ing with a high value at the beginning of the training

and gradually decreasing the value deﬁned during the

training execution according to a pre-deﬁned value of

DropRate. This way, updating weights during train-

ing is more subtle in the ﬁnal stages of training. We

came to the conclusion, after several experiments, that

a ﬁxed learning rate value of 0.001 for control ﬂow

and 0.01 for data ﬂow obtained the best results for the

programs present in the Defects4J database.

3.3 Selection of Faulty Programs

We selected a subset of the Defect4J programs to

conduct the experiment with control and data ﬂow

spectra. The data used were previously collected by

Pearson et al. using GZoltar comprise six programs,

namely: Chart, Closure, Lang, Math, Mockito and

Time, totaling 395 faulty versions (Pearson et al.,

2017).

Nevertheless, not all fault versions of the Defect4J

repository could be utilized in our experiment due to

Jaguar’s limitations to generate data ﬂow spectra. We

refer the reader to the site

of the experiment for the

list of discarded versions and the motivations for their

removal, as well to the procedures carried out to pre-

pare the data for the experiment.

3.4 Data Collection

In order to be able to conduct evaluations to answer

the research questions, we obtained the spectra from

the execution of the programs present in the Defects4J

dataset. To this end, spectra based on control ﬂow

(nodes) and data ﬂows (DUAs) were used.

Statement coverage was previously generated by

Pearson et al. (2017) using GZoltar

whereas DUA

data were previously generated by Silva and Chaim

(2021) using Jaguar

3.5 Fault Localization

From the node and DUA coverage data previously

generated, fault localization techniques based on as-

sociation metrics (Tarantula and Ochiai) and machine

learning (DNN) were applied to obtain the suspicious-

ness rates for each covered line.

In what follows, we present the steps taken to ap-

ply the fault localization techniques, namely, identi-

ﬁcation of defective lines, treatments for multi-defect

https://github.com/NicolasHampa/

jaguar-data-ﬂow-experiments

fault-localization.cs.washington.edu/data/

drive.google.com/drive/u/1/folders/

1ncaRLxUVRsA3RoL0I0VOZRAp4QmIfKTA

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

494

scenarios, and the operation of the pipeline to gener-

ate rankings for each technique analyzed.

3.5.1 Faulty Lines Identiﬁcation

As the coverage information generated by Jaguar and

GZoltar refers to DUAs and nodes, respectively, we

mapped the elements to their respective lines of code.

This procedure was performed for each of the buggy

versions under analysis in this experiment and will be

described below.

A feature of the Defects4J repository is that a de-

fective version for a given program may contain mul-

tiple points of change for a ﬁx to take effect. We

adopted the strategies of Pearson et al. (2017) to deal

with multi-lines defects. These strategies will de-

scribed as follows.

3.5.2 Suspiciousness Rate Draws

Fault localization techniques ﬁrst calculate suspi-

ciousness rates (scores) for each of the program el-

ements. The results are ordered in a ranked list con-

taining the analyzed elements. When two or more el-

ements have identical suspiciousness rates, making an

arbitrary choice might affect the evaluation of the re-

sults. Pearson et al. (2017) handle multiple elements

with the same suspiciousness rate as being the nth el-

ement in the output, where n is the average ranking of

these elements. We adopted the same approach.

3.5.3 Statements and DUAs Mapped into Lines

To allow a consistent evaluation, all elements (state-

ments or DUAs) were mapped into their respective

lines. Thus, fault localization techniques rankings are

sorted lists of suspected lines of code, favoring the

evaluation of the results obtained for different spec-

tra.

3.5.4 Multi-Line Bugs

Real bugs as those present in the Defects4J repository

are spread into several lines of the program. Thus,

we need to formally deﬁne when a bug is found: Is

identifying at least one of the defective lines enough?

Or do all faulty lines of the program need to be identi-

ﬁed? In this experiment, we only considered best case

scenarios, due to time limitations. In this scenario, it

sufﬁces to identify one faulty line so that the bug can

be completely understood and ﬁxed.

3.5.5 Omission Bugs

In 30% of scenarios involving real-world defects, the

ﬁx consists of adding new code rather than changing

existing code (Pearson et al., 2017). In other words,

the program itself does not contain any element that

could be considered the site of the defect: every ex-

pression, operation and statement in the program is

correct, but elements are missing. For each omission

fault, a set of candidate lines that ﬁxes the bug was

manually determined. Therefore, an omission bug is

deemed localized when any of its candidate lines is

present in the list of suspicious lines generated by a

particular fault localization technique.

3.5.6 Bugs on Non-Executable Code

In the Defects4J repository, there are real failure sce-

narios caused partially or completely by bugs present

in non-executable portions of code. We discarded

versions versions whose all buggy lines are non-

executable code. We focus in this experiment on ver-

sions that actually had at least one defective element

covered by spectra generated by GZoltar and Jaguar.

4 RESULTS

We used measures already applied in previous FL

works, such as Absolute score, FLT rank and TOP-

N score. They are brieﬂy explained as follows.

Absolute Score. Determines the absolute position

of the defective element present in the ranking pro-

duced by the FL technique. FLT Rank. For each de-

fective program, the applied FL techniques are ranked

from 1 to n, with n being the total number of tech-

niques under analysis. FLT is the acronym for Fault

Localization Technique. The FLT rank of a technique

represents the relative position of that technique com-

pared to the others (the fewer, the better). Top-N

Score. Given a previously deﬁned N position (1, 5,

10, etc.), this score indicates the percentage of defec-

tive versions (provided by the Defects4J dataset) in

which the applied FL technique was able to position

the defective element in the same position or less than

Table 1 presents the average FLT rank of all tech-

niques covered in this work. The techniques, pre-

sented in column Technique, are ordered from the best

technique to the worst in column Pos.. The Family

column indicates whether the applied technique is an

SBFL or an MLFL technique. The Spect. column in-

dicates whether the technique was applied based on

control ﬂow (Stmt) or data ﬂow (DUA) spectra. The

Aver. column represents the average score considering

all valid versions of all programs present in the De-

fects4J dataset. The table shows that Ochiai in com-

bination with control ﬂow spectra achieved the best

A Study on Different Spectra in Fault Localization

495

score.

Table 1: Average FLT score for all techniques.

Pos. Family Technique Spect. Aver.

1 SBFL Ochiai Stmt 2.85

2 SBFL Ochiai DUA 2.86

3 SBFL Tarantula DUA 3.02

4 SBFL Tarantula Stmt 3.06

5 MLFL DNN Stmt 4.52

6 MLFL DNN DUA 4.70

Table 2 presents the results in terms of Top-N

score. Columns Technique, Family, and Spect. have

the same meaning of those of Table 1. The last three

columns indicate the percentage of versions in which

the faulty element was ranked among the ﬁrst 1, 5,

and 10 positions of the ranking among all versions.

Ochiai using statements and DUAs presented the best

results, although it does not differ signiﬁcantly from

Tarantula using statements and DUAs.

Table 3 presents the FLT Rank effect size (Co-

hen’s d) (Bobbitt, 2022) for pair (Ochiai,Stmt) with

respect to other pairs of (FL technique, spectrum).

Typically, d less than 0.2 represents a negligible effect

size, less than 0.5 represents a small effect size, less

than 0.8 represents a medium effect size, and greater

than or equal to 0.8 represents a large effect size.

Regarding the absolute value of the effect size

tests for the FLT Rank, (Ochiai, Stmt) has a negli-

gible effect size in comparison to (Tarantula, Stmt),

(Ochiai, DUA), and (Tarantula, DUA). On the other

hand, it has a large effect size with regards to (DNN,

stmt) and (DNN, DUA).

Figure 1 presents a density curve containing the

distribution of the Absolute score for all faulty ver-

sions from Defects4J programs using both control

and data ﬂow spectra. The Density axis represents

the probability of an FL technique assuming a given

value. The distribution of values in the graph is pre-

sented in logarithmic scale format in terms of absolute

number of elements analyzed. The curve shows the

density of a continuous random variable distributed

on the x axis. The lower the scores obtained by a

given FL technique, the better the performance of the

Table 2: Top-N Score.

Techni- Fami- Spect. Top Top Top

que ly 1 5 10

DNN MLFL Stmt 3% 19% 26%

DNN MLFL DUA 1% 10% 14%

Ochiai SBFL Stmt 3% 30% 41%

Tarantula SBFL Stmt 3% 29% 41%

Ochiai SBFL DUA 1% 30% 41%

Tarantula SBFL DUA 1% 29% 39%

technique.

5 DISCUSSION

We organize our discussion based on the research

questions presented in Section 3. We conclude this

section with the discussion of the threats to validity.

5.1 RQ1: Best Spectrum for DNNs?

Rows 5 and 6 of Table 1 show the average FLT Score

for DNN using statement (row 5) and DUA (row 6).

FLT rank compares a particular technique against the

others. DNN using either statement or DUAs ranked

poorly against the other techniques; though, DNN

with statement performed slightly better in compar-

ison to DNN with DUAs.

The ﬁrst two rows of Table 2 present the results of

Top-1, Top-5 and Top-10 score for DNN techniques.

DNN using DUAs performed signiﬁcantly worst than

DNN using statements. The latter approach identiﬁes

twice the amount of faults at the Top-5 and Top-10

positions of the ranking and three times more at the

Top-1; though, the absolute values (3% against 1%)

for this range are quite small.

These results indicating that DNN with statements

performs better in the ﬁrst positions of the ranking is

corroborated by Figure 1. One can observe that DNN

with statements (full line in red) is signiﬁcantly better

than DNN with DUAs in the ﬁrst 10 positions com-

paring with DNN using DUAs (dashed line in red).

This situation inverts for higher positions of the rank-

ing.

The average measures of FLT score suggest a

draw between control and data ﬂow spectra being

used in DNN. However, studies (Parnin and Orso,

2011; de Souza et al., 2024) have shown that devel-

opers limit their attention to the ﬁrst positions of the

rankings. Thus, positioning the bug in those positions

is pivotal. In this sense, the top-N scores performance

suggests that statement coverage is the best spectrum

for fault localization using DNN.

5.2 RQ2: Best Spectrum for Tarantula

and Ochiai?

Considering the average FLT score (Table 1, rows 1

and 2), there is a draw between control and data ﬂow

spectra. Ochiai using either statements or DUAs ob-

tains very close averages. Similar averages are ob-

tained by Tarantula using both spectra.

Regarding the Top-N score measures, one can ob-

serve that statement coverage obtains better results

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

496

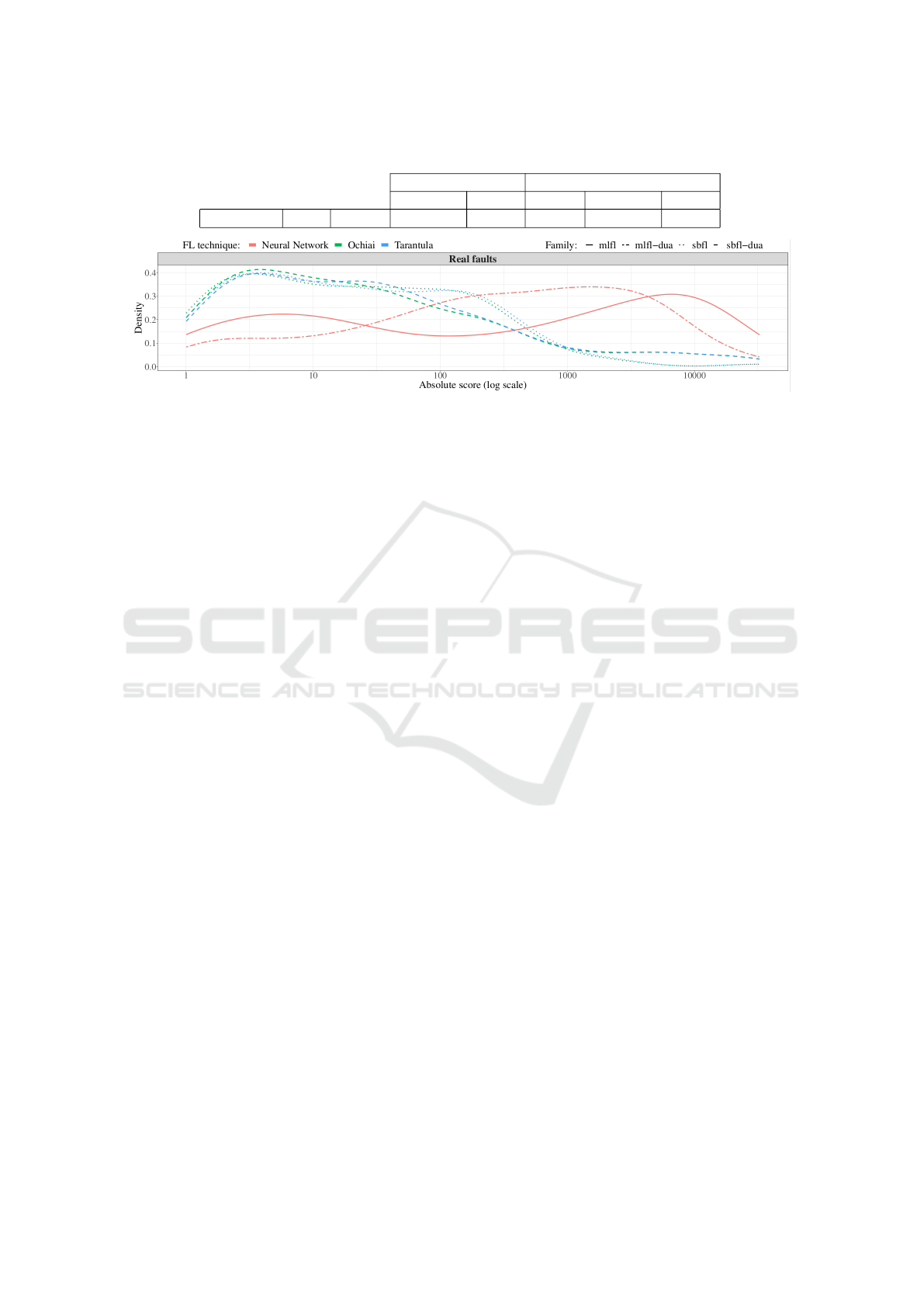
Table 3: Effect size for FLT Rank.

Stmt DUA

Tarantula DNN Ochiai Tarantula DNN

FLT rank Stmt Ochiai -0.165 -1.064 -0.004 -0.127 -1.446

Figure 1: Absolute Score density curve for all faulty versions.

for Top-1 score for both Tarantula and Ochiai while

there is a draw for Top-5 and Top-10 scores. Though

the Top-1 measure indicates a better performance for

statement coverage, it implies yet that only 3% of the

bugs are located in the ﬁrst position whereas around

40% of them are located in the ﬁrst 10 positions. The

user studies suggest that a developer will hardly check

beyond the 10th position to search for a bug, but it

seems also unlikely that s/he will only check the ﬁrst

position.

Figure 1 provides a graphical evidence of the draw

between the spectra used by SBFL techniques. The

blue and green dotted lines refer to Tarantula and

Ochiai, respectively, using statements while the blue

and green dashed lines refer to the same techniques

using DUAs. Clearly, these lines are very similar al-

most until the 100th position of the ranking suggest-

ing that there is no prevalence of a particular spec-

trum for SBFL techniques.

5.3 RQ3: Best Pair (FL Technique,

Spectrum)?

One valid question is: Which is the best approach

for fault localization using spectra? The average FLT

scores table suggests that on average DNN, indepen-

dently of the spectrum, falls behind of SBFL tech-

niques. Figure 1 indicates that the density of faults for

DNN techniques located at the ﬁrst positions of the

rankings (until the 10th position) is signiﬁcantly be-

low the density for Ochiai and Tarantula. Thus, based

on our experimental results, Tarantula or Ochiai is a

better choice for fault localization than DNN using

any spectrum.

Table 3 presents a comparison of the effect size

of the pair (Ochiai, statement) FLT rank with respect

to the other possible pairs. As expected the effect size

for such a metric of (Ochiai, statement) in comparison

to DNN techniques is medium or large.

One should bear in mind that the analyses using

averages and effect sizes presented in Tables 1 and Ta-

ble 3 take in account all 319 faulty versions. So it also

consider those versions for which (Ochiai, statement)

performed better, but positioned the buggy lines in

ranking positions that are away of the ten ﬁrst posi-

tions of the rankings.

Despite the indication that there is a draw between

spectra for SBFL techniques and the negligible effect

size for the FLT rank, if one has to choose a particular

approach, the pair (Ochiai, statement) seems to be the

best choice for fault localization in our experiment.

5.4 Threats to Validity

We address in this section the threats to the internal,

external, and conclusion validity. Threats to inter-

nal validity are related to the several scripts imple-

mented in the different stages of the experimental as-

sessment. This threat might present itself in terms of

defects present in the code of the scripts or in an in-

accurate conceptual understanding of the FL problem

explored.

External validity threats are concerned to the gen-

eralization of the results presented. Other sets of pro-

grams may obtain different results; nevertheless, a set

of six programs was used, written by different devel-

opers and focusing on different application areas. Re-

garding the comparisons between data ﬂow and con-

trol ﬂow, 319 defective versions were assessed in to-

tal.

Another threat is that our results are only applica-

ble to DNN models. There are other works that uti-

lize deep neural networks (Qian et al., 2021; Li et al.,

2021; Ghosh et al., 2022; Dutta, 2022) that achieve

better rankings. Also, there are pretraining methods

that can enhance the model parametrization (Zheng

A Study on Different Spectra in Fault Localization

497

et al., 2016). Finally, there are strategies for data treat-

ment that are not applied, like more sophisticated rep-

resentations of the coverage data (Lou et al., 2021)

Conclusion validity threats are related to the met-

rics utilized to assess the research questions. The

FLT rank metric is a way to compare FL techniques

directly, rather than just their absolute performance,

since this metric is agnostic to whether the metrics

being compared are absolute or relative. The Top-N

score metric can be better correlated with the devel-

oper’s ability to debug the code.

We make available all our results obtained to be

reproduced by a reader interested in this work. The

scripts used are available in the GIT repository

6 RELATED WORK

In the last few years, we have observed the use of

machine learning models based on neural networks

and deep learning for fault localization (Zhang et al.,

2021; Wong, 2023). Initially, control ﬂow cover-

age were mostly used together with machine learn-

ing techniques for defect localization (Wong and Qi,

2011). Other works, though, have started using spec-

tra based on data ﬂow (Li et al., 2021; Jo et al., 2021;

Ren et al., 2022).

Ren et al. (2022), Li et al. (2021), Jo et al. (2021)

combine data and control ﬂow spectra to train dif-

ferent machine learning models (radial basis neu-

ral network, convolutional neural network, and back-

propagation neural network, respectively) for fault lo-

calization. Thus, these works focus on the combina-

tion of spectra as fault localization techniques, but not

in the analysis of the performance of different spectra

in MBFL.

On the other hand, in the SBFL realm, previ-

ous works have addressed the comparison of dif-

ferent spectra for fault location. Santelices et al.

(2009) indicate that DUAs are better than statements

and branches when used in SBFL techniques to lo-

cate bugs. Masri (2010) points out that DIFA—

Dynamic Information Flow Analysis, also a data ﬂow

spectrum—, DUA and branch spectra, performed bet-

ter than statement spectrum. Ribeiro et al. (2019)

investigate how data ﬂow coverage, notably, DUA,

compares to line coverage. Their results suggest that

up to 50% more faults are ranked in the Top-15 posi-

tions using data ﬂow spectra in comparison with line

spectra.

However, Santelices et al. (2009) and Masri

(2010) use few and small (in terms of lines of code)

https://github.com/NicolasHampa/

jaguar-data-ﬂow-experiments

faulty programs, and, for the most part, containing

bugs artiﬁcially inserted into the programs. Ribeiro

et al. (2019) use 163 faulty versions selected from De-

fects4J repository, and faulty versions from JSoup’s

own repository.

Our study experiment with 319 faulty versions

from Defects4J’s Chart, Closure, Math, Mockito, and

Time, and with a MBFL technique (DNN) and two

SBFL techniques (Ochiai and Tarantula).

7 CONCLUSIONS

We presented an experiment whose goal was to in-

vestigate how control and data ﬂow spectra impact

on the performance of fault localization techniques.

We experimented with one MBFL (Deep Neural

Networks—DNN) and two SBFL (Ochiai and Taran-

tula) techniques.

Our results suggest that DNN using statement

spectra generate more effective rankings in compar-

ison to DNN using DUAs. On the other hand, SBFL

techniques like Ochiai and Tarantula do not present a

prevalence of either type of spectra, especially when

one focus the attention on the ﬁrst ten positions of the

rankings. Finally, we analyzed which pair (fault lo-

calization technique, spectrum) performs best in our

experiment. (Ochiai, statement) seems to be the best

pair, though, the effect sizes are negligible or small

with respect to Tarantula using statements or DUAs

and Ochiai using DUAs.

We believe our experiment is one more piece of

evidence towards a better understanding of the role of

spectra in fault localization. We intend to apply the

same experimental design for MBFL using convolu-

tional Deep Neural Networs and expand the number

and the diversity of faulty programs in further experi-

ments.

REFERENCES

Abreu, R., Zoeteweij, P., and van Gemund, A. J. (2007).

On the accuracy of spectrum-based fault localiza-

tion. In Testing: Academic and Industrial Confer-

ence Practice and Research Techniques - MUTATION

(TAICPART-MUTATION 2007), pages 89–98.

Bobbitt, Z. (2022). Statology. How to Calculate Cohen’s d

in R (With Example).

de Souza, H. A., Chaim, M. L., and Kon, F. (2016).

Spectrum-based software fault localization: A sur-

vey of techniques, advances, and challenges. CoRR,

abs/1607.04347.

de Souza, H. A., de Souza Lauretto, M., Kon, F., and Chaim,

M. L. (2024). Understanding the use of spectrum-

ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering

498

based fault localization. J. Softw. Evol. Process.,

36(6).

Dutta, A. (2022). Poster: Ebﬂ-an ensemble classiﬁer

based fault localization. In 2022 IEEE Conference on

Software Testing, Veriﬁcation and Validation (ICST),

pages 473–476.

Ghosh, D., Singh, J. P., and Singh, J. (2022). An adaptive

approach for fault localization using r-cnn. In 2022

International Conference on Advancements in Smart,

Secure and Intelligent Computing (ASSIC), pages 1–6.

Jo, J.-H., Lee, J., Jaffari, A., and Kim, E. (2021). Fault lo-

calization with data ﬂow information and an artiﬁcial

neural network. International Journal of Software In-

novation (IJSI), 9(3):66–78.

Jones, J. A., Harrold, M. J., and Stasko, J. (2002). Visual-

ization of test information to assist fault localization.

page 467–477, New York, NY, USA. Association for

Computing Machinery.

Just, R., Jalali, D., and Ernst, M. D. (2014). Defects4j: A

database of existing faults to enable controlled test-

ing studies for java programs. In Proceedings of the

2014 International Symposium on Software Testing

and Analysis, ISSTA 2014, page 437–440, New York,

NY, USA. Association for Computing Machinery.

Li, Y., Wang, S., and Nguyen, T. (2021). Fault localiza-

tion with code coverage representation learning. In

2021 IEEE/ACM 43rd International Conference on

Software Engineering (ICSE), pages 661–673.

Lou, Y., Zhu, Q., Dong, J., Li, X., Sun, Z., Hao, D.,

Zhang, L., and Zhang, L. (2021). Boosting coverage-

based fault localization via graph-based representa-

tion learning. In Proceedings of the 29th ACM Joint

Meeting on European Software Engineering Confer-

ence and Symposium on the Foundations of Software

Engineering, ESEC/FSE 2021, page 664–676, New

York, NY, USA. ACM.

Masri, W. (2010). Fault localization based on informa-

tion ﬂow coverage. Softw. Test. Veriﬁcation Reliab.,

20(2):121–147.

Parnin, C. and Orso, A. (2011). Are automated debugging

techniques actually helping programmers? In Pro-

ceedings of the 20th International Symposium on Soft-

ware Testing and Analysis, ISSTA 2011, Toronto, ON,

Canada, July 17-21, 2011, pages 199–209. ACM.

Pearson, S., Campos, J., Just, R., Fraser, G., Abreu, R.,

Ernst, M. D., Pang, D., and Keller, B. (2017). Evalu-

ating and improving fault localization. In Proceedings

of the 39th International Conference on Software En-

gineering, ICSE ’17, page 609–620. IEEE Press.

Qian, J., Ju, X., and Chen, X. (2023). Gnet4ﬂ: effective

fault localization via graph convolutional neural net-

work. Automated Software Engineering, 30(2):16.

Qian, J., Ju, X., Chen, X., Shen, H., and Shen, Y. (2021).

Agﬂ: A graph convolutional neural network-based

method for fault localization. In 2021 IEEE 21st Inter-

national Conference on Software Quality, Reliability

and Security (QRS), pages 672–680.

Rapps, S. and Weyuker, E. (1985). Selecting software test

data using data ﬂow information. IEEE Transactions

on Software Engineering, SE-11(4):367–375.

Ren, S., Zuo, X., Chen, J., and Tan, W. (2022). Statement

spectrum with two dimensional eigenvalues for intelli-

gent software fault localization. Journal of Intelligent

& Fuzzy Systems, 42:2899–2914. 4.

Ribeiro, H. L., de Araujo, R. P. A., Chaim, M. L., de Souza,

H. A., and Kon, F. (2019). Evaluating data-ﬂow cov-

erage in spectrum-based fault localization. In 2019

ACM/IEEE International Symposium on Empirical

Software Engineering and Measurement, ESEM 2019,

Porto de Galinhas, Recife, Brazil, September 19-20,

2019, pages 1–11. IEEE.

Santelices, R., Jones, J. A., Yanbing Yu, and Harrold, M. J.

(2009). Lightweight fault-localization using multiple

coverage types. In 2009 IEEE 31st International Con-

ference on Software Engineering, pages 56–66.

Silva, D. L. d. and Chaim, M. L. (2021). Impacto da relac¸

de subsunc¸

ao na localizac¸

ao de defeitos baseados em

espectros de ﬂuxo de dados. Master’s thesis, Escola

de Artes, Ci

encias e Humanidades, Universidade de

ao Paulo, S

ao Paulo.

Wong, E. and Qi, Y. (2011). Bp neural network-based effec-

tive fault localization. International Journal of Soft-

ware Engineering and Knowledge Engineering, 19.

Wong, W. E. (2023). Machine Learning-Based Techniques

for Software Fault Localization, pages 297–319.

Yan, Y., Jiang, S., Wang, R., Zhang, C., Wang, C., Zhang,

S., and Wen, M. (2022). A fault localization approach

based on birnn and multi-dimensional features. Inter-

national Journal of Software Engineering and Knowl-

edge Engineering, 32(08):1179–1201.

Zakari, A., Lee, S., Alam, K., and Ahmad, R. (2018). Soft-

ware fault localisation: A systematic mapping study.

IET Software, 13.

Zhang, Z., Lei, Y., Mao, X., Yan, M., Xu, L., and Zhang, X.

(2021). A study of effectiveness of deep learning in

locating real faults. Information and Software Tech-

nology, 131:106486.

Zheng, W., Hu, D., and Wang, J. (2016). Fault localization

analysis based on deep neural network. Mathematical

Problems in Engineering, 2016:1–11.

Zhuo, Z., Lei, Y., Tan, Q., Mao, X., Zeng, P., and Chang,

x. (2017). Deep learning-based fault localization with

contextual information. IEICE Transactions on Infor-

mation and Systems, E100.D:3027–3031.

A Study on Different Spectra in Fault Localization

499