Teaching Parallel Programming on the CPU Based on Matrix

Multiplication Using MKL, OpenMP and SYCL Libraries

Emilia Bober

and Beata Bylina

Maria Curie-Skłodowska University, Pl. M. Curie-Skłodowskiej 5, 20-031 Lublin, Poland

Keywords:

Parallel Matrix Multiplication, OpenMP, SYCL, MKL.

Abstract:

Matrix multiplication is a fundamental operation in engineering computations. With the widespread use of

modern multi-core processors, this operation can be signiﬁcantly accelerated through parallel programming.

Consequently, it is essential to acquaint computer science students with parallel programming techniques.

Matrix multiplication is well known to students, while additionally offering numerous possibilities for par-

allelisation. This makes it an ideal example for introducing parallel programming while highlighting key

considerations such as execution time, accuracy of the calculations, code complexity and the impact of the

hardware architecture on the results obtained. Students can implement and test such software themselves. In

this paper, the performance and accuracy of the MKL, SYCL and OpenMP libraries are investigated using

matrix multiplication of different sizes as an example. OpenMP is discussed at some universities, so it may

already be familiar to students, whereas SYCL is a newer and less commonly used standard but it offers great

possibilities. Square matrices with double-precision elements and dimensions of 4096×4096, 8192×8192,

and 16384×16384 were selected for testing. The experiments revealed signiﬁcant computational speed-ups

compared to the sequential algorithm, with no loss of accuracy. SYCL was found to be about 10 times faster

than OpenMP, but the calculations performed with MKL are by far the fastest. Additionally, the results indi-

cated that doubling the number of threads does not directly correlate to a twofold increase in execution speed,

and doubling the matrix size in each dimension leads to an approximately tenfold increase in execution time.

1 INTRODUCTION

Parallel computing has become an integral part of

mainstream computing, driven by the widespread

availability of multi-core processors(Sitsylitsyn,

2023)(Czarnul et al., 2024). As a result, applications

will be able to perform their tasks in parallel to take

full advantage of the bandwidth gains of multicore

processors. However, writing parallel code remains

signiﬁcantly more complex than writing sequential

code. Therefore, it is worth devoting time to this

issue in the education of computer science students

(Marowka, 2008)(Gao and Zhang, 2010)(Bro

danac

et al., 2022). Matrix multiplication is one of the most

essential operations in scientiﬁc computing (Ade-

femi, 2024). The matrices on which operations are

performed have increasingly large sizes, even several

thousand elements in one dimension. Multiplying

such large matrices with a classical algorithm without

any libraries using parallelism or multithreading

https://orcid.org/0009-0000-6466-8796

https://orcid.org/0000-0002-1327-9747

takes many hours even on modern processors. It is

usually impossible to wait that long for a result, so

it is necessary to consider the available solutions

both in terms of libraries and the distributed matrix

multiplication algorithms themselves. Basic matrix

multiplication can be written:

C = A × B (1)

If A is a matrix of dimension n × k and B is a matrix

of dimension k × m, then C is a matrix of dimension

n × m, where each element c

i j

is calculated from the

formula:

i j

∑

k=1

· b

k j

(2)

Such a way is called naive. Its complexity is O(n

The naive algorithm is not the only possible algorithm

for matrix multiplication (Golub and Loan, 2013).

There are several algorithms for concurrent matrix

multiplication, including the Cannon and Strassen al-

gorithms (Ballard et al., 2014). Currently available

multi-core processors allow parallel computing. It

is also possible to use several processor cores in a

Bober, E. and Bylina, B.

Teaching Parallel Programming on the CPU Based on Matrix Multiplication Using MKL, OpenMP and SYCL Libraries.

DOI: 10.5220/0013279100003932

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 2, pages 713-720

ISBN: 978-989-758-746-7; ISSN: 2184-5026

713

naive algorithm using appropriate libraries such as

OpenMP and SYCL. These approaches signiﬁcantly

reduce computation time compared to sequential pro-

grams (Ogunyiola et al., 2024). Matrix multiplica-

tion is a subject well known to every computer sci-

ence student. It is a straightforward operation, with a

basic algorithm that is simple to understand and im-

plement. The operation can be parallelized in many

ways. It is therefore a good example for introducing

students to more advanced topics like parallel pro-

gramming. When teaching parallel programming, it

is crucial to emphasize key aspects such as program

execution time and computational accuracy. This arti-

cle contains example implementations of parallel ma-

trix multiplication and the results of measuring the

time and accuracy of calculations. Students in paral-

lel programming courses can make such implemen-

tations on their own to then test their performance

and accuracy of computation. The aim of this pa-

per is to present methods for teaching parallel pro-

gramming on CPU, due to its widespread availability.

The paper discusses the library optimized for Intel

processors, such as MKL, and the popular OpenMP

standard, as well as the modern framework SYCL.

This analysis allows students to understand the im-

pact of hardware architecture and code optimization

on performance. In this paper Intel processor was

chosen to run the tests, but it is not the only option.

It is possible to use run such tests on another archi-

tecture. Other programming languages can also be

used to work with OpenMP and SYCL. In this article,

C++ was chosen because it is well known to students

and widely used. However, the paper omits GPUs

to avoid complications related to heterogeneous com-

puting systems. This article presents timing results

for a naive sequential algorithm without using any li-

braries for parallel computing, as well as results using

OpenMP and SYCL. Additionally, the performance

of matrix multiplication using the MKL library is ana-

lyzed. The tests assess the accuracy of each approach

by comparing the results to the sequential naive al-

gorithm, with the mean square error (MSE) serving

as the accuracy metric. The naive sequential algo-

rithm is used as the benchmark. The results obtained

in this paper show that SYCL performs the compu-

tation faster than OpenMP, while maintaining similar

accuracy.However, both libraries lag signiﬁcantly be-

hind MKL in terms of execution speed for this im-

plementation. Therefore, it is worth presenting this

solution to students to encourage them to extend their

knowledge in this area and further optimise their code

and learn about algorithms dedicated to distributed

matrix multiplication. Chapter 2 describes libraries

chosen to present in this paper. Chapter 3 provides

a description of an example exercise that can be car-

ried out during classes with students. Chapter 4 con-

tains the implementation of the algorithms using the

libraries discussed. These include code fragments of

the programmes, together with a description of how

they were compiled so that they can be reproduced.

Chapter 5 describes the testing environment, includ-

ing relevant environment variables and a description

of the numerical experiment itself. Chapter 6 presents

the experimental results: execution times, computa-

tional accuracy, and speed-ups relative to the baseline

algorithm. Chapter 7 provides a summary and out-

lines potential directions for future research.

2 LIBRARIES

In this paper OpenMP and SYCL libraries were cho-

sen for the study because they allow software de-

velopment for heterogeneous systems. This implies

code portability between CPU and GPU, which is a

basis for further research. However, this article fo-

cuses exclusively on a single hardware conﬁguration:

a multi-core CPU with shared memory. The portabil-

ity of solutions between CPUs and GPUs is beyond

the scope of this work. Intel MKL library is also

included in the comparison. Intel Math Kernel Li-

brary (MKL) is an advanced mathematical library op-

timised for performance on Intel processors that sup-

ports a wide range of computational operations such

as linear algebra (including double-precision matrix

multiplication), Fourier transforms, statistics or vec-

tor functions. With optimised algorithms and the abil-

ity to automatically adapt to the hardware architec-

ture, MKL allows computational applications in areas

such as machine learning, scientiﬁc simulation or en-

gineering modelling to be signiﬁcantly accelerated. It

supports a variety of programming languages, includ-

ing C, C++ and Fortran, and integrates with popular

frameworks, making it a versatile tool for developers.

Using MKL can reduce computation time, enabling

faster results and more efﬁcient use of available hard-

ware resources (Intel Corporation, ). OpenMP (Open

Multi-Processing) is a widely-used parallel program-

ming tool that enables the effective use of multi-

threading in applications running on today’s multi-

core processors. It is an open standard that integrates

with popular programming languages such as C, C++

and Fortran, allowing code to be easily extended with

parallel functionality using special directives, library

functions and environment variables. Thanks to its

ﬂexibility, OpenMP allows programmers to control

the division of tasks between threads, synchronisa-

tion, as well as resource management, making it sig-

CSEDU 2025 - 17th International Conference on Computer Supported Education

714

niﬁcantly easier to optimise application performance

(OpenMP Architecture Review Board, ). A number of

scientiﬁc papers have been written examining this li-

brary against other solutions (Ismail et al., 2011)(Pen-

nycook et al., 2019). Some universities have OpenMP

in the curriculum, so the tool may be familiar to some

students. SYCL (Standard for C++ Parallelism and

Heterogeneous Computing) is an open standard de-

veloped by the Khronos Group that enables parallel

programming across diverse hardware platforms, in-

cluding CPUs, GPUs, and accelerators. SYCL takes

advantage of modern features of the C++ language,

allowing developers to write code in a uniform way,

regardless of the target architecture. Its abstraction

model, based on data buffering and dependency man-

agement, simpliﬁes the development of complex par-

allel applications while maintaining efﬁciency (The

Khronos Group, )(Reinders et al., 2023). SYCL is a

new standard that rarely appears in scientiﬁc papers,

especially in the context of matrix multiplication.

3 EXERCISE IN CLASS WITH

STUDENTS

In this course, students complete an exercise to im-

plement parallel matrix multiplication using OpenMP

and SYCL. The goal of this exercise is to demon-

strate how these technologies can speed up compu-

tations while introducing students to the practical as-

pects of parallel programming. Students ﬁrst imple-

ment a matrix multiplication algorithm using sim-

ple parallelization techniques such as parallel loops

in OpenMP. They then extend their solution using

SYCL, which requires them to understand the con-

cept of explicit data management and computation in

kernels. Once the implementation is complete, they

compare the performance of their programs by mea-

suring their runtimes for different matrix sizes and

numbers of threads. As a reference, they use the MKL

library to see how their implementations compare to

highly optimized code. Students encounter various

challenges during the exercise. Controlling the com-

putational environment, such as by conﬁguring envi-

ronment variables such as OMP_NUM_THREADS

in OpenMP or SYCL-speciﬁc settings, can be difﬁcult

but is essential for obtaining consistent comparative

results. Another challenge is the appropriate selec-

tion of optimization ﬂags in the icpx compiler, which

have a signiﬁcant impact on code performance. Stu-

dents also learn that increasing the number of threads

does not always translate into a linear increase in per-

formance, which prompts them to analyze the effect

of reducing the number of threads by half. The exer-

cise also includes a comparison of the accuracy of cal-

culation results obtained using OpenMP and SYCL

with the results generated by the MKL library. This

allows students to understand how different tools af-

fect the precision of calculations. Through such an

assignment, students not only learn about parallel

programming tools, but also develop analytical skills

and critical thinking. Example exercise description:

Write a program that uses OpenMP and SYCL tools

to perform parallel matrix multiplication, using for-

mula (2). The program should be compiled using

the icpx compiler with appropriate optimization op-

tions. Choose options for self-compilation. Measure

the program’s runtime and then conduct a numerical

experiment on a multicore machine, adjusting the ap-

propriate environmental options. Analyze the com-

parison of execution times for OpenMP and SYCL to

choose the most efﬁcient code. Compare the obtained

results with the execution times for matrix multiplica-

tion using the MKL library. Finally, investigate the

impact of changing the number of threads, testing dif-

ferent values, including half of the available proces-

sor cores. Additionally, check how the used tools af-

fect the accuracy of the computational results, com-

paring them with the results obtained using the MKL

library.

4 IMPLEMENTATION

This chapter contains the most important parts of the

programme codes, which will allow the results ob-

tained to be reproduced. These can be used for further

research or to present the issue of parallel program-

ming to students. Below is the code showing how

timing was measured in all implementations. Only

the matrix multiplication time without data initialisa-

tion was always measured.

double start_time = dsecnd();

matrix multiplication

double end_time = dsecnd();

double elapsed_time = end_time - start_time;

The listing below shows a code fragment of a sequen-

tial matrix multiplication programme:

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

for (int p = 0; p < k; ++p)

C[i * n + j] +=

A[i * k + p] * B[p * n + j];

A command was used to compile the program for

sequential matrix multiplication: icpx -lmkl_core -

lmkl_intel_ilp64 -lmkl_sequential -O3 -o program pro-

gram.cpp

Teaching Parallel Programming on the CPU Based on Matrix Multiplication Using MKL, OpenMP and SYCL Libraries

715

• lmkl_core – link option with the Intel Math Ker-

nel Library (MKL) containing basic mathematical

functions such as matrix and vector operations.

• lmkl_intel_ilp64 – link option with a version of

MKL adapted to work with 64-bit indices and in-

teger indices (ILP64).

• lmkl_sequential – link option with a version of

MKL that runs sequentially, without parallel exe-

cution. This can be useful when you want to avoid

thread management issues or when parallelism is

managed in other ways in your application.

• O3 – The compiler optimisation ﬂag indicates

the highest level of optimisation that attempts to

maximise the performance of the generated code,

at the expense of longer compilation times and

higher memory consumption.

Code snippet which shows parallel matrix multiplica-

tion using OpenMP:

#pragma omp parallel for schedule(dynamic)

num_threads(num_threads)

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

for (int p = 0; p < k; ++p)

C[i * n + j] +=

A[i * k + p] * B[p * n + j];

The directive #pragma omp parallel for sched-

ule(dynamic) num_threads(num_threads) is re-

sponsible for the parallel execution of the loop

for. num_threads variable stores the set number of

threads, i.e. 16 and 32.

Code snippet which shows parallel matrix mul-

tiplication using SYCL:

std::vector<double> C(N * N, 0.0);

std::vector<double> B(N * N, 0.0);

std::vector<double> A(N * N, 0.0);

sycl::queue queue(sycl::cpu_selector_v);

double* d_A =

sycl::malloc_device<double>(N * N, queue);

double* d_B =

sycl::malloc_device<double>(N * N, queue);

double* d_C =

sycl::malloc_device<double>(N * N, queue);

Data initialization

...

queue.memcpy(d_A, A.data(),

N * N * sizeof(double)).wait();

queue.memcpy(d_B, B.data(),

N * N * sizeof(double)).wait();

sycl::range<2> global_range(N, N);

queue.submit([&](sycl::handler& cgh) {

cgh.parallel_for(global_range,

[=](sycl::id<2> idx) {

size_t row = idx[0];

size_t col = idx[1];

double sum = 0.0;

for (size_t k = 0; k < N; ++k) {

sum += d_A[row * N + k] * d_B[k * N + col];

}

d_C[row * N + col] = sum;

});

}).wait();

SYCL queue is created from sycl::queue

queue(sycl::cpu_selector_v). The SYCL queue

is the primary task management mechanism for

programming in SYCL. It is an abstract interface for

managing the execution of operations on devices.

The queue allows memory management on the de-

vice, including memory allocation and deallocation,

and data transfer between host memory (CPU) and

device memory. The SYCL queue accepts tasks to be

executed on the device, deﬁned by so-called kernel

functions (kernel functions). These tasks can be

executed in parallel on multiple threads or compute

units of the device. global_range deﬁnes the total

scope of the calculation as a 2D grid with dimensions

NxN. queue.submit() sends a task (lambda function)

to the SYCL queue for parallel execution on the

device. In the lambda function (parallel_for), each

thread identiﬁed by idx computes an element of the

resulting matrix C (stored in d_C) by performing

matrix multiplication of the corresponding elements

from matrices A (stored in d_A) and B (stored in

d_B).

id<2> is a generic type in SYCL that represents a ho-

mogeneous identiﬁer or index in a two-dimensional

space. A command was used to compile the pro-

gramme using SYCL: icpx -fsycl -lmkl_core

-lmkl_sequential -lmkl_intel_ilp64 -O3 -fsycl-

targets=spir64_x86_64 program.cpp -o program

• fsycl – ﬂag informs the compiler that the source

ﬁle program.cpp is written in SYCL.

5 NUMERICAL EXPERIMENT

All the programmes discussed were run and tested

on the hardware and software conﬁguration described

next. When teaching parallel programming, the stu-

dents’ attention should be drawn to the dependence of

the results on the environment conﬁguration. This is

both a hardware aspect and a software conﬁguration.

In the case of hardware, the most important aspects

will be: the generation of the processor, its architec-

ture, the number of cores, clocking and whether the

processor supports virtual cores. In terms of software,

the operating system, the version of the compiler and

libraries, and all necessary environment variables will

CSEDU 2025 - 17th International Conference on Computer Supported Education

716

be important. Students should be able to assess the

performance of their algorithm implementation and

the suitability of a given hardware and software con-

ﬁguration for parallel computing. They should also

estimate which conﬁguration will be more beneﬁcial.

This article presents the computational results of the

proposed implementations on a single but powerful

hardware conﬁguration. Students are advised to per-

form the tests on smaller arrays, due to less powerful

hardware conﬁgurations of home computers and lap-

tops.

5.1 Environment

The tests of the prepared programmes were performed

on a hardware platform with an Intel Xeon Gold

5218R processor, 2.10GHz, with x86_64 architecture.

This processor has 40 cores, 80 threads. The available

RAM is 376GB. AlmaLinux 8.7 operating system is

installed on the server. All programs were compiled

using Intel oneAPI DPC++/C++ Compiler 2024.0.2.

5.2 Tests

Each program was executed 3 times with the CPU un-

burdened by other tasks. The environment variable

KMP_AFFINITY=granularity=ﬁne,compact,1,0 was set

before any program was executed. This variable is

used by the OpenMP library to control the assign-

ment of threads to processors. Granularity speciﬁes

the level of detail at which threads are assigned to

computing units. A value of ﬁne means that threads

are assigned at the level of individual processor cores.

This is the most accurate level, providing the most

control over thread assignment. Compact is a CPU

thread assignment strategy in which threads are as-

signed sequentially to the nearest available cores, in

a compact manner. The aim is to maximise memory

locality. 1 speciﬁes the interval between thread as-

signments. 0 is the initial core from which threads

will be assigned. The environment variables used to

control the execution of the SYCL program are:

DPCPP_CPU_NUM_CUS=16

DPCPP_CPU_PLACES=cores

DPCPP_CPU_CU_AFFINITY=close The ﬁrst variable

above sets the number of threads used by the pro-

gramme. The second variable determines that only

physical cores will be used, without hyperthreading.

The third variable inﬂuences that threads will be as-

signed to the available cores one at a time. Each of

the programs examined performs calculations using

the same matrix multiplication algorithm discussed

above, but uses different options for parallelizing the

calculations. The basic programme is a sequential

matrix multiplication according to the formula above.

No parallelization is used here. The master matrices

for the libraries under study will be calculated using

this algorithm. The second method is to parallelize

the calculations using OpenMP. The OpenMP library

is a well-known tool with an established track record.

The third method is to program using SYCL. SYCL

is an open programming standard developed by the

Khronos Group that enables programming of hetero-

geneous computer systems such as CPU, GPU and

other accelerators. The standard ensures code porta-

bility between platforms. Source code for different

devices can be written in a single ﬁle. SYCL uses

the C++ language to deﬁne parallel computing. The

last method is to calculate the product of a matrix us-

ing the cblas_dgemm function from the MKL library.

The function dsecnd() from the MKL library was used

to measure timing in all programmes. For this reason,

this library was added to the compilation of each pro-

gramme. All programmes have been compiled with

the -O3 ﬂag to optimise their performance. Pseudo-

random double-precision numbers ranging from -1 to

+1 were used to initialise the A and B matrices. The

double precision allows 15-17 signiﬁcant digits to be

stored. Matrix C is the result of multiplying matrices

A and B using the algorithm under study. C_base ma-

trix is the result of multiplying matrices A and B us-

ing a function implementing the naive algorithm with-

out using additional libraries to parallelize the calcu-

lations. The mean squared error (MSE), which we de-

ﬁne according to the formula, was chosen to compare

the validity of the results:

MSE =

∑

i=1

base

− C

)

(3)

6 RESULTS

This section presents the results of measuring the

computation time and accuracy and the speed-up of-

fered by the different implementations of the matrix

multiplication algorithm. The results are divided ac-

cording to the library used, the number of threads and

the size of the matrix. Table 1 contains the calcu-

lated mean squared error that was generated by the

analysed implementations of the matrix multiplica-

tion algorithm. The benchmark matrices were gen-

erated by the sequential algorithm. The table 2 shows

the results of the execution time measurements of the

individual programs. The results have been divided

according to the size of the matrix, the library used

and the number of CPU threads that were used by the

analysed programs. A useful performance indicator

for the computing libraries under study is the acceler-

Teaching Parallel Programming on the CPU Based on Matrix Multiplication Using MKL, OpenMP and SYCL Libraries

717

ation of programme execution. Such acceleration can

be deﬁned as

, where : (4)

— execution time of the sequential programme,

— programme execution time using the library

under test.

The calculated acceleration values can be found in

the table 3. The graphs show the execution time

of the programmes as a function of matrix size, sep-

arately for the sequential algorithm, OpenMP, SYCL

and MKL. It can be seen from the data presented

Figure 1: Execution time of the sequential algorithm de-

pending on the matrix size.

Figure 2: Execution time with OpenMP depending on the

matrix size.

Figure 3: Program execution time with SYCL depending on

the matrix size.

that even the slowest of the parallel solutions is nearly

12 times faster than executing the algorithm sequen-

tially. In the case of the fastest - the acceleration is

several thousand times, and the time itself is reduced

to a few seconds or even fractions of a second for

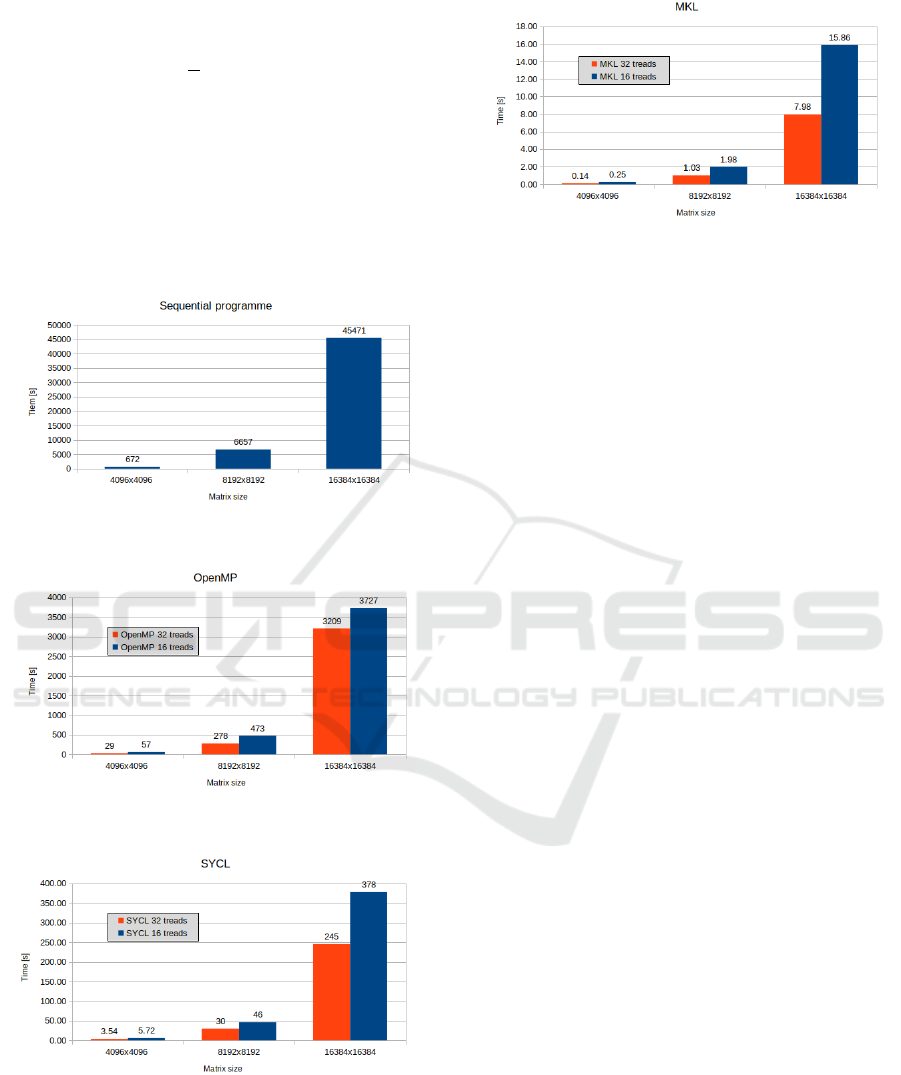
Figure 4: Program execution time with MKL depending on

the matrix size.

smaller matrices. The effect of the number of threads

on the execution time of a programme is not obvious.

Twice as many threads is not twice as fast program

execution time. MKL is very close to this assump-

tion, but for OpenMP and SYCL this difference is

smaller, although still signiﬁcant. The largest speed-

up was obtained for an 8192x8192 matrix regardless

of the library used. The accuracy of the calculations

for all algorithms, expressed by the mean squared er-

ror, varies on the order of E−28 to E−26, as can be

well seen in table 1. As the size of the multiplied ma-

trices increases, the accuracy of the calculations de-

creases, but the difference is negligible. The mean

squared error between the smallest and the largest of

the matrices tested differs by only one order of mag-

nitude, i.e. in the worst case it is E−26. As we can

see, all the errors are very small, much better than the

precision of the used type. Thus, we can say that the

algorithm’s accuracy is very high. Increasing the size

of the matrix had a signiﬁcant impact on programme

execution time. And this increased from 6.8 times to

11.6 times with respect to a smaller matrix. The MKL

library allows the greatest acceleration of calculations

without signiﬁcant loss of accuracy. This library was

developed by Intel, so it is the best optimised. Un-

fortunately, an implementation of this library is not

publicly available. Implementing the sequential algo-

rithm and parallelizing it with SYCL gives very good

results. Computations are performed several hundred

times faster and the loss of accuracy is small.

7 CONCLUSIONS

This paper presents a method for teaching parallel

programming on CPU based on matrix multiplication,

using the MKL, OpenMP and SYCL libraries. The

computations were performed exclusively on a CPU,

without GPU involvement. The OpenMP, SYCL and

MKL libraries were used to perform parallel calcula-

tions. These results can serve as a starting point for

teaching parallel programming using OpenMP and

CSEDU 2025 - 17th International Conference on Computer Supported Education

718

Table 1: Mean squared error of the calculation result relative to the sequential algorithm.

Threads Programme 4096x4096 8192x8192 16384x16384

16 MKL 2.14E-27 3.34E-26 3.34E-26

OpenMP 2.26E-27 3.69E-26 3.69E-26

SYCL 1.70E-28 1.26E-27 1.26E-27

32 MKL 2.25E-27 8.81E-27 3.45E-26

OpenMP 2.24E-27 9.24E-27 3.64E-26

SYCL 1.53E-28 4.56E-28 1.28E-27

Table 2: Average execution time [s] of individual programs with a given number of threads for a given matrix size.

Threads Programme 4096x4096 8192x8192 16384x16384

1 sequential 671.980 6657.370 45471

16 OpenMP 57.108 472.861 3727.160

SYCL 5.717 46.059 377.856

MKL 0.252 1.979 15.857

32 OpenMP 29.385 277.650 3208.817

SYCL 3.541 29.801 245.405

MKL 0.138 1.035 7.983

Table 3: Acceleration of program execution relative to a sequential algorithm.

Threads Programme 4096x4096 8192x8192 16384x16384

16 OpenMP 11.8 14.1 12.2

SYCL 117.5 144.5 120.3

MKL 2666.6 3364 2867.6

32 OpenMP 22.9 24 14.2

SYCL 189.8 223.4 185.3

MKL 4869.4 6432.7 5696

SYCL on an example of a matrix multiplication op-

eration familiar to students. Students are encouraged

to independently implement the matrix multiplica-

tion algorithm, parallelize it using libraries such as

OpenMP or SYCL, and evaluate their results. They

can also compare their outcomes with the benchmarks

described in this article, noting the impact of hard-

ware conﬁgurations on performance. In the tests de-

scribed in this article, SYCL was found to be 9.6

to 13.2 times faster than OpenMP. Intel’s MKL li-

brary, optimized for high performance, signiﬁcantly

outperformed both, with computation speeds 20 to 30

times faster than SYCL. However, it should be re-

membered that our implementation was a parallelized

classical algorithm and the MKL implementation is

likely to be a block algorithm, which may have an

impact on performance. Another aspect compared

in the paper was the effect of matrix size on pro-

gram execution time. Doubling the matrix size in

each dimension increased execution time by a fac-

tor of 6.8 to 11.6 across all solutions analyzed. The

accuracy of all implementations, measured using the

mean squared error (MSE), was comparable, ranging

from 10

−28

to 10

−26

, demonstrating that all libraries

maintained high precision. When teaching parallel

programming, these dependencies between algorithm

design, parallelization approach, and hardware con-

ﬁguration should be highlighted. Students should in-

dependently implement and parallelize the algorithm,

conduct tests, and analyze their results. For aca-

demic applications, it is advisable to perform tests for

smaller matrix sizes due to the long execution time of

the sequential programme, which provides a bench-

mark. The SYCL library is worth exploring in further

research work. It allows code portability between the

CPU and GPU, which can result in performance gains

without signiﬁcantly increasing the effort required to

write the programme. The results on the CPU were

satisfactory. Future research could also focus on im-

plementing and parallelizing alternative algorithms,

such as Cannon’s or Strassen’s, using OpenMP and

SYCL. Comparing these methods could provide ad-

ditional perspectives on optimizing parallel computa-

tion for matrix operations.

REFERENCES

Adefemi, T. (2024). Analysis of the performance of the ma-

trix multiplication algorithm on the cirrus supercom-

Teaching Parallel Programming on the CPU Based on Matrix Multiplication Using MKL, OpenMP and SYCL Libraries

719

puter. arXiv preprint, arXiv:2408.15384.

Ballard, G., Demmel, J., Dumitriu, I., and Holtz, O. (2014).

A framework for practical parallel fast matrix multi-

plication. arXiv preprint, arXiv:1409.2908.

Bro

danac, P., Novak, J., and Boljat, I. (2022). Has the

time come to teach parallel programming to secondary

school students? Heliyon, 8(1).

Czarnul, P., Matuszek, M., and Krzywaniak, A. (2024).

Teaching high–performance computing systems–a

case study with parallel programming apis: Mpi,

openmp and cuda. In International Conference on

Computational Science, pages 398–412. Springer.

Gao, Y. and Zhang, X. (2010). A teaching schema for multi-

core programming. In CSEDU (2), pages 195–198.

Golub, G. H. and Loan, C. F. V. (2013). Matrix Computa-

tions. Johns Hopkins University Press, 4th edition.

Intel Corporation. Intel oneMKL: Math Kernel Li-

brary for High-Performance Computing. Online,

https://www.intel.com/content/www/us/en/developer

/tools/oneapi/onemkl.html.

Ismail, M. A., Mirza, S. H., and Altaf, T. (2011). Concur-

rent matrix multiplication on multicore architectures.

International Journal of Computer Science and Secu-

rity (IJCSS), 5(2):142–149.

Marowka, A. (2008). Think parallel: Teaching parallel pro-

gramming today. IEEE Distributed Systems Online,

9(8):1–1.

Ogunyiola, K., Jackson, S., Prokhorenkova, L., et al.

(2024). Evaluation of computational and power per-

formance in matrix multiplication methods and li-

braries on cpu and gpu using mkl, cublas, and sycl.

arXiv preprint, arXiv:2405.17322.

OpenMP Architecture Review Board. The OpenMP API

Speciﬁcation for Parallel Programming. Online,

https://www.openmp.org/.

Pennycook, S. J., Sewall, J. D., and Lee, V. W. (2019). Im-

plications of a metric for performance portability. Fu-

ture Generation Computer Systems, 92:947–958.

Reinders, J., Ashbaugh, B., Brodman, J., Kinsner, M., Pen-

nycook, J., and Tian, X. (2023). Data Parallel C++:

Programming Accelerated Systems Using C++ and

SYCL. Springer Nature.

Sitsylitsyn, Y. (2023). A systematic review of the literature

on methods and technologies for teaching parallel and

distributed computing in universities. Ukrainian Jour-

nal of Educational Studies and Information Technol-

ogy, 11(2):111–121.

The Khronos Group. SYCL: C++ Single-source Het-

erogeneous Programming for Accelerators. Online,

https://www.khronos.org/sycl/.

CSEDU 2025 - 17th International Conference on Computer Supported Education

720