Dynamic Hierarchical Token Merging for Vision Transformers

Karim Haroun

1,2 a

, Thibault Allenet

1 b

, Karim Ben Chehida

1 c

and Jean Martinet

2 d

Université Paris-Saclay, CEA, List, F-91120 Palaiseau, France

Université Côte d’Azur, I3S, CNRS, France

Keywords:

Vision Transformers, Token Merging, Neural Network Compression, Dynamic Neural Networks.

Abstract:

Vision Transformers (ViTs) have achieved impressive results in computer vision, excelling in tasks such as

image classiﬁcation, segmentation, and object detection. However, their quadratic complexity O(N

), where

N is the token sequence length, poses challenges when deployed on resource-limited devices. To address this

issue, dynamic token merging has emerged as an effective strategy, progressively reducing the token count

during inference to achieve computational savings. Some strategies consider all tokens in the sequence as

merging candidates, without focusing on spatially close tokens. Other strategies either limit token merging

to a local window, or constrains it to pairs of adjacent tokens, thus not capturing more complex feature rela-

tionships. In this paper, we propose Dynamic Hierarchical Token Merging (DHTM), a novel token merging

approach, where we advocate that spatially close tokens share more information than distant tokens and con-

sider all pairs of spatially close candidates instead of imposing ﬁxed windows. Besides, our approach draws

on the principles of Hierarchical Agglomerative Clustering (HAC), where we iteratively merge tokens in each

layer, fusing a ﬁxed number of selected neighbor token pairs based on their similarity. Our proposed approach

is off-the-shelf, i.e., it does not require additional training. We evaluate our approach on the ImageNet-1K

dataset for classiﬁcation, achieving substantial computational savings while minimizing accuracy reduction,

surpassing existing token merging methods.

1 INTRODUCTION

The advent of Vision Transformers (ViTs) (Dosovit-

skiy et al., 2020) has sparked signiﬁcant advances

in computer vision, demonstrating robust perfor-

mance in image classiﬁcation (Liu et al., 2021)(Tou-

vron et al., 2021), segmentation (Zhang et al.,

2022)(Strudel et al., 2021), and object detection tasks

(Carion et al., 2020)(Liu et al., 2024). Since the intro-

duction of the Vision Transformer (ViT), researchers

have successfully adapted Transformers, originally

designed for Natural Language Processing (NLP), to

process images by treating local patches of an im-

age as sequential tokens. Through the self-attention

mechanism, ViTs learn the relationships between

these tokens, achieving high-level visual understand-

ing across a range of applications.

Despite these successes, ViTs have a notable

limitation: their computational complexity scales

https://orcid.org/0009-0000-6972-6019

https://orcid.org/0009-0003-0810-3338

https://orcid.org/0000-0002-5959-1832

https://orcid.org/0000-0001-8821-5556

~22%~30%~39%~50%

Complexity reduction ratio

~10%

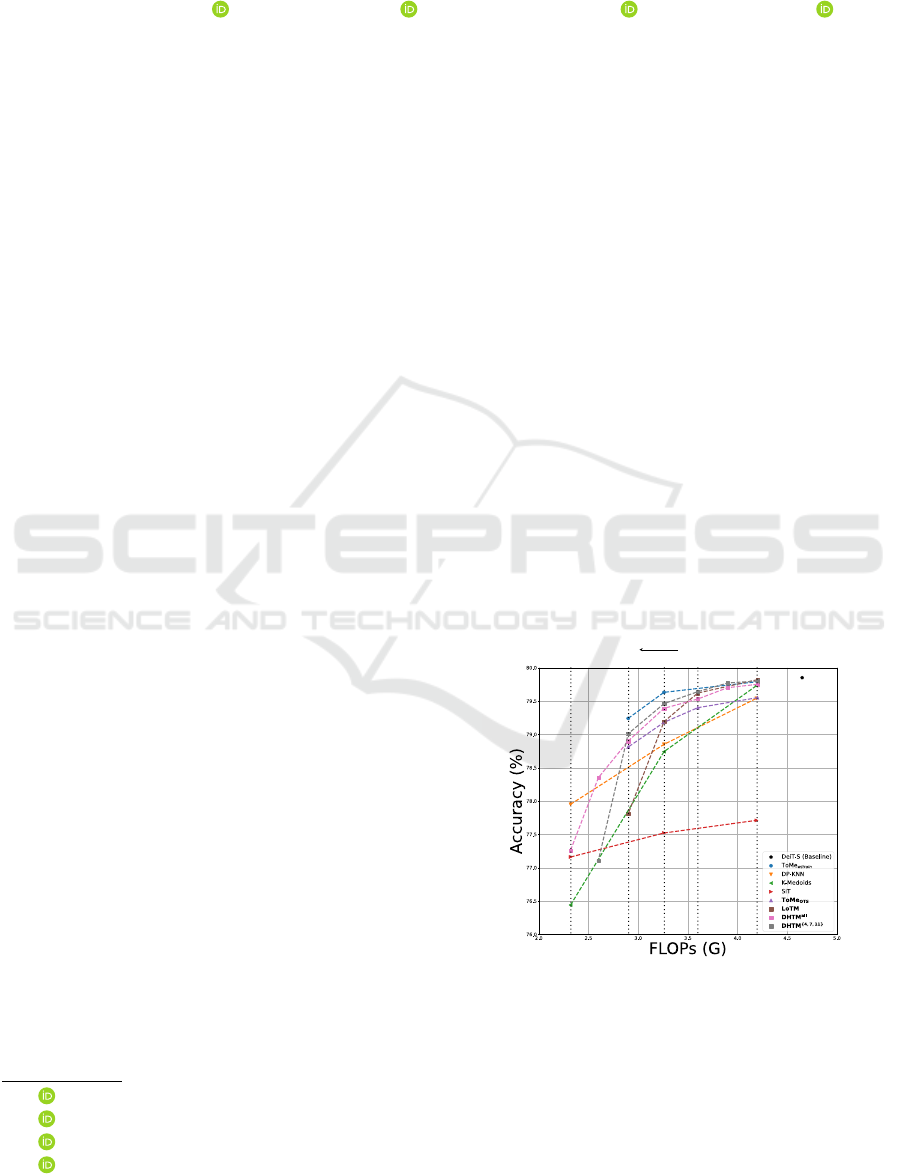
Figure 1: Performance of DHTM against existing methods

on DeiT-Small (Touvron et al., 2021). We highlight in bold

the off-the-shelf strategies, i.e., when no further training is

required. We use the subscripts w/train and OTS for ToMe

(Bolya et al., 2023) to distinguish between the off-the-shelf

and the trained variants. The superscripts on DHTM de-

notes if the merging strategy is applied to all layers or em-

pirically selected ones. The vertical dotted lines show com-

plexity reduction ratio (FLOPs).

Haroun, K., Allenet, T., Ben Chehida, K. and Martinet, J.

Dynamic Hierarchical Token Merging for Vision Transformers.

DOI: 10.5220/0013284100003912

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 3: VISAPP, pages

677-684

ISBN: 978-989-758-728-3; ISSN: 2184-4321

677

quadratically with respect to the number of tokens in

the sequence. This O(N

) complexity, where N is

the number of tokens, often limits their deployment

on resource-constrained devices. Therefore, reducing

the token sequence length has emerged as a practical

strategy to make ViTs more computationally efﬁcient,

improving their adaptability to various hardware con-

straints while maintaining low accuracy reduction.

Among these, dynamic token reduction tech-

niques are particularly prominent, encompassing two

main strategies: token pruning and token merging.

Token pruning selectively removes less signiﬁcant to-

kens from the sequence, while token merging com-

bines similar tokens, effectively fusing information

and reducing redundancy. Both methods reduce com-

plexity dynamically, i.e., at inference. This often re-

sults in a drop in accuracy, therefore, the main chal-

lenge is to ﬁnd the optimal accuracy vs. complex-

ity tradeoff. While token pruning effectively reduces

computational load, it has two limitations. First, it

risks losing crucial information, which may degrade

model performance. Second, the variability in token

importance across different inputs complicates batch

processing. For these reasons, we focus on token

merging approaches in this work.

In this paper, we propose Dynamic Hierarchical

Token Merging (DHTM), a novel token merging strat-

egy. Rather than selecting a single, ﬁxed reference

token and performing merging within a limited win-

dow, DHTM treats each token as a potential reference,

iteratively expanding its region by merging with the

most similar neighboring tokens in each Transformer

layer. Our method is grounded on Hierarchical Ag-

glomerative Clustering (HAC) (Ward Jr, 1963) and

applies clustering in a localized manner, preserving

essential information while minimizing information

loss when merging tokens. By progressively merging

tokens based on the highest similarities in each re-

gion, DHTM achieves efﬁcient token reduction, sig-

niﬁcantly improving computational efﬁciency while

minimizing accuracy reduction. As shown in Figure

1, DHTM effectively balances information loss with

computational gains, offering a selective and thor-

ough merging process that enhances model perfor-

mance on ImageNet-1K dataset. The main contribu-

tions of this work are as follows:

• We introduce a DHTM, a spatially-aware token

merging approach that iteratively combines simi-

lar neighboring tokens.

• We validate the effectiveness of our approach

through extensive experiments on the ImageNet-

1K dataset, showcasing that our method can re-

duce computational complexity while minimizing

accuracy reduction.

• We evaluate the performance of DHTM against

recent state-of-the-art token merging techniques,

including global candidate evaluation and local

window token merging strategies.

• We validate the merging criteria, i.e, the co-

sine similarity measure, through an ablation study

against random merging.

2 RELATED WORKS

Vision Transformers (ViTs) traditionally process im-

ages by dividing them into a uniform grid of patches,

with each patch treated as a token. However, not all

regions of an image equally contribute to task per-

formance, highlighting the need for efﬁcient token

management strategies. This section reviews Vision

Transformers and state-of-the-art token merging tech-

niques.

2.1 Vision Transformers

The ﬂexibility of ViTs in handling variable-length in-

puts is a key feature that allows them to process mul-

tiscale visual inputs without requiring different sets of

parameters. Each input image is divided into patches,

projected to a latent space, and treated as tokens.

While the number of tokens can vary depending on

the image resolution or scale, the Transformer archi-

tecture is designed to handle this variability. The em-

bedding size of each token is ﬁxed, denoted as d

, en-

suring that each token is represented as a vector of the

same dimensionality. Therefore, the input sequence

of N tokens can be expressed as follows:

T = {t

,. ..,t

} where t

∈ R

(1)

Each token t

is projected into three distinct repre-

sentations: the query (Q), the key (K), and the value

(V). The query Q encodes how much focus a token

should receive, the key K encodes its relevance to

other tokens, and the value V represents the con-

tent to be attended to. These projections are com-

puted as Q = TW

, K = TW

, and V = TW

, where

∈ R

×d

are learnable weight matrices,

and d

is the dimensionality of the query and key vec-

tors.

The Multi-Head Self-Attention (MHSA) mecha-

nism processes tokens pairwise by calculating atten-

tion scores for every token pair, as deﬁned by the fol-

lowing equation:

MHSA(Q,K,V ) = softmax



√



V (2)

VISAPP 2025 - 20th International Conference on Computer Vision Theory and Applications

678

Merging

unit

Multi-Head Attention (MHA)

Feed-Forward Network (FFN)

Next layer

Input sequence

Layer 1 Layer L

Output sequence

(M < N)

Input RGB image

Output visualization

Compute similarity of

all adjacent pairs

Get the most similar pair

Merge the most

similar pair

Iteration 1

Blobs after k iterations

Iteration k

Classification layer

(MLP)

Model output

Class_id 94:

Hummingbird

k times

Figure 2: Overview of the DHTM method. Starting with an initial token set, we iteratively identify the most similar adjacent

token pairs between t

and its neighbors C. Then, we merge the most similar adjacent pair based on their cosine similarity,

offering more ﬂexibility than methods that restrict merging to local windows, while incorporating locality compared to ap-

proaches that merge distant tokens. Our strategy lies in the middle, leveraging both properties.

Similarly, the Multi-Layer Perceptron (MLP)

layer that follows self-attention processes each to-

ken independently, applying the same transforma-

tion across all tokens due to their ﬁxed embedding

size. This design allows Transformers to generalize

over varying input sizes while maintaining param-

eter efﬁciency. However, despite their advantages,

ViTs exhibit quadratic complexity relative to the num-

ber of tokens, which increases the computational de-

mand. The total number of Floating Point Operations

(FLOPs) for a single Transformer layer can be ex-

pressed as follows:

(N,d

) = Φ

MHSA

(N,d

) + Φ

MLP

(3)

= 12Nd

+ 2N

(4)

This quadratic complexity highlights the need for

efﬁcient token processing methods to mitigate the

computational burden associated with larger input

sizes. To address this challenge, researchers have pro-

posed various token reduction strategies. The follow-

ing subsection reviews state-of-the-art of token merg-

ing techniques, focusing on their strengths and limi-

tations.

2.2 Token Merging

Token merging combines tokens based on a sim-

ilarity measure to improve efﬁciency. DPC-KNN

(Zeng et al., 2022) determines clusters by evaluat-

ing token density and merging those with minimal

distance to higher-density points. SiT (Zong et al.,

2022) and Sinkhorn (Haurum et al., 2022) use assign-

ment matrices derived from learned queries to com-

bine tokens. PatchMerger (Renggli et al., 2022) uses

a dot-product softmax operation with preset queries

for clustering. K-Medoids (Marin et al., 2023) ap-

plies a hard-clustering algorithm that iteratively min-

imizes Euclidean distances within clusters, using at-

tention scores from the CLS token to initialize clus-

ter centers. In ToMe (Bolya et al., 2023), tokens are

split into two groups, with each token in one group

paired and merged with its closest match in the other

group by averaging their representations. Finally,

LoTM (Haroun et al., 2024) constrains the merging to

pairs of horizontally-adjacent tokens, relying on co-

sine similarity.

While these methods advance token merging, they

have several limitations. PatchMerger (Renggli et al.,

2022) and ToMe (Bolya et al., 2023) operate by

evaluating all tokens globally as potential merging

candidates, allowing distant clusters to be merged

without emphasizing spatial relations, as spatially

close tokens tend to share more semantic informa-

tion than distant ones. Other approaches use a ﬁxed

local window around a predeﬁned reference token,

referred to as a centroid in these papers, to merge

the most similar tokens within that window (Zeng

et al., 2022)(Marin et al., 2023). Although promis-

Dynamic Hierarchical Token Merging for Vision Transformers

679

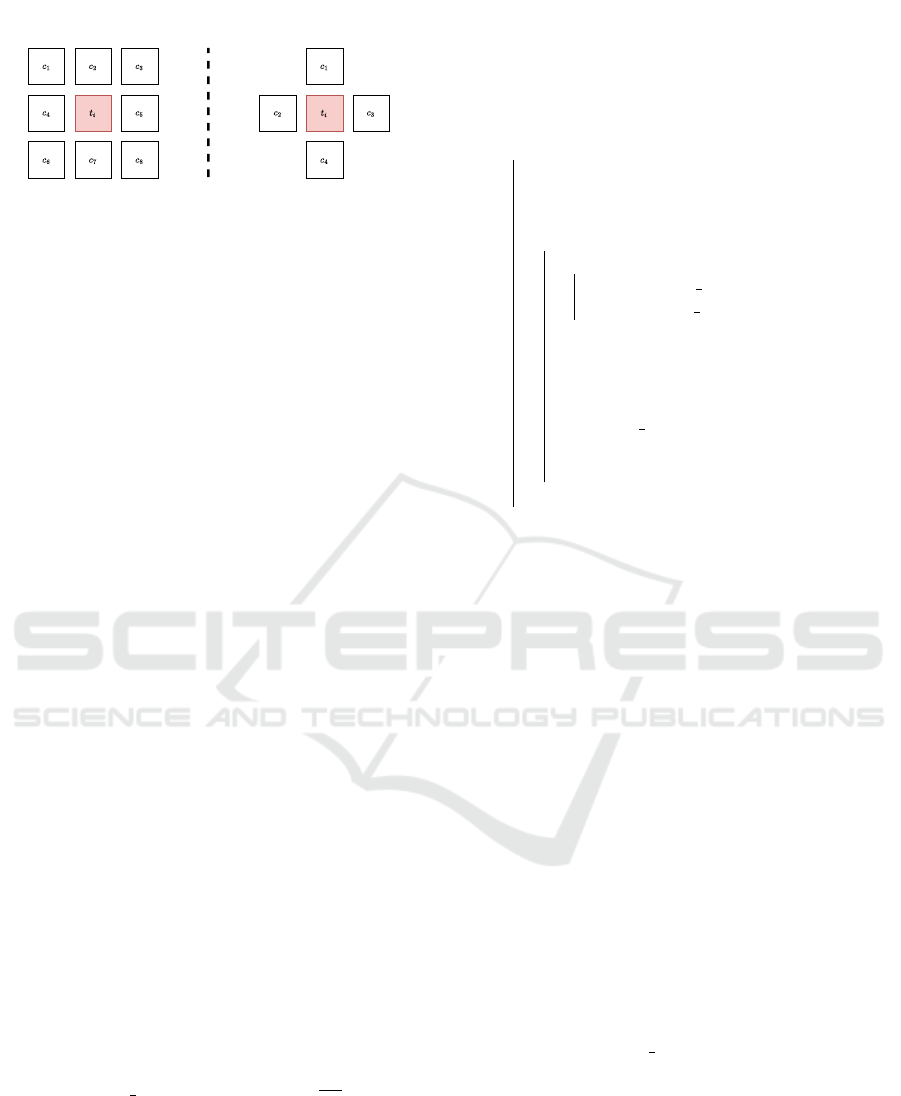
8-connectivity 4-connectivity

Figure 3: A 2D illustration of neighbor connectivity types.

Left: 8-connectivity with all 8 neighbor tokens; Right: 4-

connectivity, restricted to four horizontal and vertical neigh-

bors. In DHTM, we use the 8-connectivity setting, as we

test for all possible neighbors without restrictions.

ing, this constrained approach hinders the beneﬁts of

locality by setting rigid priors, such as reference to-

kens and the merging window. Lately, strategies like

LoTM (Haroun et al., 2024) restrict merging candi-

dates to two horizontally adjacent tokens, which is an

extreme case in local merging between a pair of candi-

dates. This restriction may hinder the method’s ability

to capture more complex relationships and features

among tokens. In contrast, our approach, consid-

ers all tokens as potential references and selectively

merges only the most similar neighboring tokens in

each Transformer layer, thus striking a balance be-

tween unrestricted and restrictive strategies.

3 METHODOLOGY

3.1 Token Merging

Let Z ∈ R

N×d

denote the output token sequence

from the Multi-Head Self-Attention (MHSA) layer,

depicted in Eq (2), where N is the number of tokens

and d

is the embedding dimension.

We deﬁne a similarity measure S : R

×R

→

R for pairs of tokens. This similarity measure can

be expressed as the inverse of the Euclidean distance,

the inverse of the norm, or simply cosine similarity,

although the latter is most commonly used.

Next, let I ⊆ {1, ..., N} represent a set of indices

of tokens identiﬁed for merging based on a predeﬁned

threshold of similarity. The merging operation is de-

ﬁned as follows:

merged

= avg merge({Z

| i ∈ I }) =

|I |

∑

i∈I

(5)

where merge(z

) represents the average merge of

and z

. After determining the merging results for

selected pairs of tokens, the new token sequence can

be expressed as follows:

′

{

| k /∈ I

}

∪{z

merged

} (6)

Data: Set of tokens T = {t

,. . .,t

Number of selected Transformer layers

L, Number of merges per layer N

merge

Result: Final set of merged tokens T

′

1 Initialize T

′

← T ;

2 for each selected layer l = 1 to L do

3 M ← 0; // Merge count

4 σ ← []; // Similarity score

5 C ← []; // Neighbors

6 while M < N

merge

7 for each token t

∈ T

′

8 C ←C + get neighbors(t

′

);

9 σ ← σ + get similarities(t

,C);

10 end

/* Get the most similar pair

11 (t

) ←C[argmax

(σ[k])];

12 t

← avg merge(t

);

13 T

′

← (T

′

\{t

}) ∪{t

} ;

14 M ← M + 1;

15 end

16 end

17 return T

′

; // len(T

′

) < len(T )

Algorithm 1: DHTM algorithm.

In this formalization, Z

′

represents the updated to-

ken sequence after the merging operation, which re-

duces the sequence length.

3.2 Dynamic Hierarchical Token

Merging (DHTM)

In this section, we provide additional information

about the proposed DHTM strategy, which is de-

scribed in Algorithm 1, in addition to the impor-

tant steps. DHTM operates on an initial set of to-

kens T = {t

,. . .,t

}, obtained from the outputs of

multi-head self-attention. The algorithm initializes a

working set of tokens, denoted as T

′

, which serves as

the basis for merging operations.

In each Transformer layer, DHTM ﬁrst retrieves

the spatial neighbors of each token t

∈ T

′

C = get neighbors(t

′

) (7)

This operation ensures that the token merging pro-

cess is local, focusing on nearby tokens, while test-

ing all possible adjacent pairs of the sequence T

′

without predeﬁning hard merging windows or refer-

ence tokens, as shown in Figure 3 where we use the

8-connectivity setting for DHTM. Additionally, our

method also supports an alternative type of neighbor

connectivity, which is the 4-connectivity, where we

constrain the connectivity to horizontal and vertical

VISAPP 2025 - 20th International Conference on Computer Vision Theory and Applications

680

neighbors. After obtaining the neighbors, the algo-

rithm evaluates the similarity between the token t

and

each of its neighbors t

∈ C using a similarity mea-

sure:

σ = get similarities(t

,C) (8)

This similarity measure quantiﬁes how alike the to-

kens are, allowing for a more informed merging de-

cision. While DHTM uses cosine similarity, other

similarities or distance measures can be used, such

as Euclidean distance, Manhattan distance or KL-

divergence.

The algorithm then selects the neighbor with the

highest similarity score and returns the best pair to

merge:

) = C[argmax(S)] (9)

This selection process ensures that, in each itera-

tion, DHTM merges only the most similar token pairs,

maintaining meaningful semantic information. Once

the best neighbor is identiﬁed, the algorithm performs

the average merging of the tokens:

= avg merge(t

) (10)

The merged token t

then replaces the original to-

kens in T

′

, effectively reducing the sequence length.

As shown in Figure 2, this merging process continues

iteratively until the speciﬁed number of merges N

merge

is reached for the current layer.

4 EXPERIMENTS

4.1 Dataset, Benchmarks and

Comparison

We conduct our experiments on the ImageNet-1K

dataset (Deng et al., 2009), a widely used bench-

mark for evaluating image classiﬁcation models.

ImageNet-1K contains over 1.2 million training im-

ages across 1.000 classes, with a validation set of

50.000 images, providing a diverse and comprehen-

sive dataset to assess model performance.

To validate the effectiveness of our proposed Dy-

namic Hierarchical Token Merging (DHTM) method,

we use the DeiT (Touvron et al., 2021) model as

a backbone. Speciﬁcally, we evaluate our approach

on three variants: DeiT-Tiny, DeiT-Small, and DeiT-

Base. For comparison, we consider state-of-the-art

token merging techniques on the same backbone.

4.2 Evaluation Metrics

The performance of our method is evaluated using

two primary metrics: computational complexity and

classiﬁcation accuracy. We report the computational

complexity in terms of Floating Point Operations

(FLOPs), which is a standard measure for model ef-

ﬁciency, which we measure using the fvcore

library.

We evaluate classiﬁcation performance using the top-

1 accuracy on the ImageNet-1K validation set, reﬂect-

ing the percentage of correctly classiﬁed images.

4.3 Implementation Details

As mentioned above, DHTM is designed to integrate

into existing Transformer architectures without re-

quiring additional training. During the evaluation, the

batch size was set to 1. Additionally, in each selected

layer, we iteratively merge k times, where k is prede-

ﬁned.

4.4 Experiment Results

For a comprehensive comparison, we benchmark

DHTM against several state-of-the-art token reduc-

tion methods, including SiT (Zong et al., 2022),

Sinkhorn (Haurum et al., 2022), PatchMerger (Reng-

gli et al., 2022), K-Medoids (Marin et al., 2023),

DPC-KNN (Zeng et al., 2022), ToMe (Bolya et al.,

2023), and LoTM (Haroun et al., 2024), based on the

evaluation metrics depicted above.

Figure 1 depicts the performance of DHTM

against state-of-the-art techniques on DeiT-Small

(Touvron et al., 2021), given various computa-

tional budgets. We observe that for aggressive

merging ratios exceeding 39%, DHTM

all

performs

better than DHTM

{4,7,11}

, K-medoids, and SiT,

while slightly trailing behind DP-KNN. Furthermore,

DHTM demonstrates a key advantage by enabling

higher compression ratios compared to other strate-

gies, such as ToMe.

Since DHTM

{4,7,11}

shows higher performance

than DHTM

all

for reduction ratios below 39%, we

will use this conﬁguration for the next experiments.

Therefore, we will refer to it simply as DHTM for

clarity.

Table 1 shows the performance of DHTM on three

DeiT variants (Tiny, Small, and Base) with varying

k values, illustrating the trade-off between accuracy

and FLOPs. The results indicate that increasing k

reduces FLOPs across models, with the largest re-

ductions for higher k values, while the top-1 accu-

https://github.com/facebookresearch/fvcore

Dynamic Hierarchical Token Merging for Vision Transformers

681

Table 1: DHTM performance comparison on DeiT (Tou-

vron et al., 2021) models at different k values, where k de-

notes the number of merges applied in each selected layer.

k = 0 represents the baseline, and k = 56 represents the most

constrained conﬁguration.

DeiT-Tiny

k Top-1(%) FLOPs(G)

0 72.20 1.26

10 72.17 1.16

20 72.10 1.07

30 71.95 0.97

40 71.66 0.88

48 71.28 0.81

56 69.98 0.75

DeiT-Small

k Top-1(%) FLOPs(G)

0 79.82 4.65

10 79.80 4.21

20 79.77 3.92

30 79.64 3.63

40 79.46 3.26

48 79.01 2.90

56 77.11 2.60

DeiT-Base

k Top-1(%) FLOPs(G)

0 81.85 17.60

10 81.84 16.54

20 81.72 15.48

30 81.55 14.43

40 81.11 13.97

48 80.68 12.34

56 80.10 11.74

racy exhibits only a slight decline. Besides, we no-

tice that the decrease in accuracy is less pronounced

in the more complex DeiT-Base model, which has a

larger embedding dimension (d

= 384) twice that of

DeiT-Small (d

= 768) and four times that of DeiT-

Tiny (d

= 192). Larger embedding reduces the sen-

sitivity to token merging, which allows more aggres-

sive merging in DeiT-Base with minimal performance

loss. This allows us to optimize computation efﬁ-

ciently while preserving accuracy, especially in larger

models.

In table 2, we show the performance of DHTM

against various state-of-the-art methods across three

different models: DeiT-Tiny, DeiT-Small, and DeiT-

Base. DHTM is an off-the-shelf method that re-

quires no training and can be easily integrated into

any model, offering a plug-and-play solution, as are

LoTM and ToMe

OT S

. In contrast, ToMe

w/train

(Bolya

Table 2: Performance evaluation of DHTM against existing

methods for a reduction ratio of 30% in terms of FLOPs,

we highlight Top-1 accuracy and FLOPs. W/o train means

off-the-shelf variants, i.e., no additional training required,

and w/train depicts variants that require training.

Method Top-1(%) FLOPs(G)

w/ train

DeiT-Tiny 72.20 1.26

Sinkhorn 53.19 0.88

PatchMerger 66.81 -

SiT 68.99 -

DPC-KNN 70.10 -

K-Medoids 69.90 -

ToMe

w/train

71.74 -

w/o train

ToMe

OT S

70.94 -

LoTM 70.76 -

DHTM 71.66 -

w/ train

DeiT-Small 79.82 4.65

Sinkhorn 64.02 3.26

PatchMerger 75.80 -

SiT 77.52 -

K-Medoids 78.74 -

DPC-KNN 78.85 -

ToMe

w/train

79.63 -

w/o train

ToMe

OT S

79.18 -

LoTM 79.19 -

DHTM 79.46 -

w/ train

DeiT-Base 81.85 17.60

Sinkhorn 63.36 12.34

PatchMerger 74.52 -

SiT 76.63 -

DPC-KNN 79.06 -

K-Medoids 79.98 -

ToMe

w/train

81.05 -

w/o train

ToMe

OT S

80.75 -

LoTM 80.01 -

DHTM 80.68 -

et al., 2023) requires training from scratch for 300

epochs, which increases computational cost. Finally,

the results presented in the table are for k = 40, cor-

responding to a 30% reduction in complexity com-

pared to the baseline. In the following paragraphs, we

analyze the performance of our model on three DeiT

variants compared to existing methods.

For the DeiT-Tiny model, the resource-

constrained variant of DeiT, DHTM achieves

71.66% accuracy with 0.88G FLOPs at k = 40.

DHTM outperforms Sinkhorn, PatchMerger, SiT,

DPC-KNN, and K-Medoids by more than 1.5%. In

addition, it slightly outperforms LoTM by 0.90%,

indicating that restricting the merge to only two

adjacent tokens may not fully capture the complexity

of feature similarities. Finally, DHTM outperforms

ToMe

OT S

, an off-the-shelf variant of ToMe by 0.72%,

VISAPP 2025 - 20th International Conference on Computer Vision Theory and Applications

682

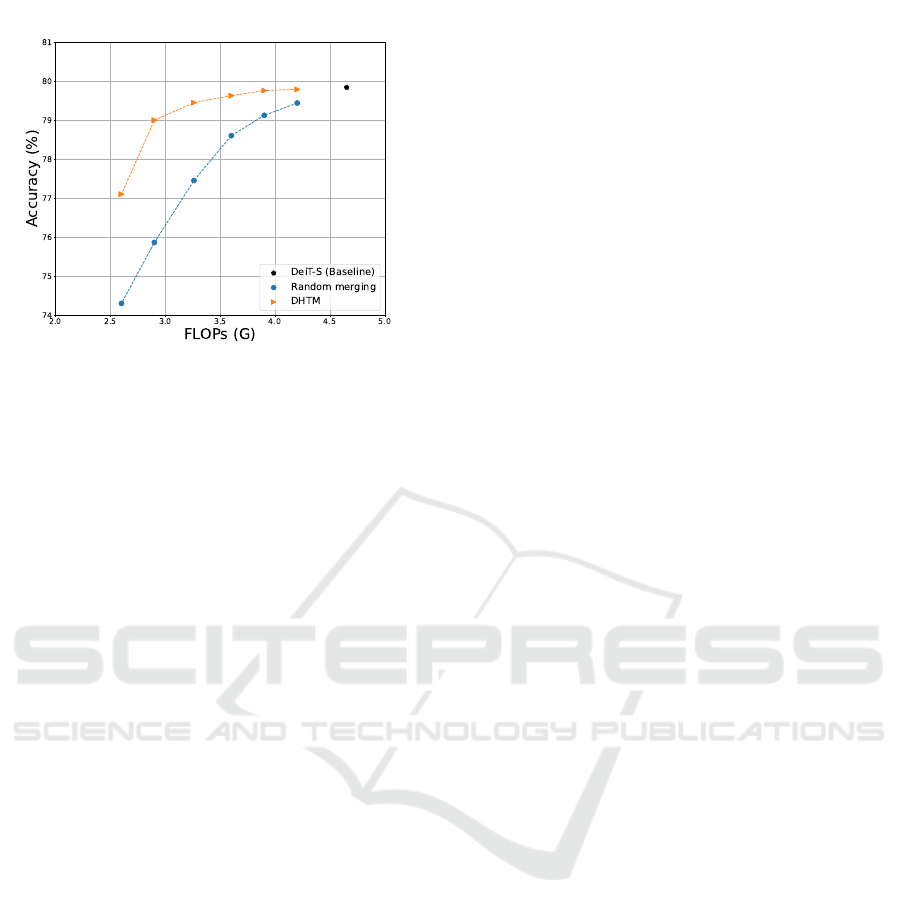
Figure 4: Comparison of DHTM with random token merg-

ing on DeiT-Small. The results clearly show that the ran-

dom merging approach (in blue) experiences a signiﬁcant

drop in performance, particularly under more constrained

scenarios as the number of merging candidates increases,

while DHTM (in orange) maintains superior performance.

and performs almost identically to ToMe

w/train

, with

a minimal difference of just 0.08%.

For the DeiT-Small model, DHTM achieves

79.46% accuracy with 3.26G FLOPs at k = 40.

DHTM outperforms Sinkhorn, PatchMerger, SiT by

2% or higher, and K-Medoids, DPC-KNN by at least

0.61%. In addition, it slightly surpasses ToMe

OT S

and LoTM by 0.28% and 0.27%, respectively, demon-

strating the best performance for off-the-shelf mod-

els. Although it falls short by 0.17% compared to

ToMe

w/train

, this difference is minimal considering

DHTM’s off-the-shelf deployment capability, unlike

ToMe, which requires training.

Finally, DHTM achieves 80.68% accuracy with

12.34G FLOPs at k = 40 for DeiT-Base model.

DHTM signiﬁcantly outperforms Sinkhorn, Patch-

Merger, SiT, by more than 4.5%, and DP-KNN, K-

Medoids by more than 1%. Furthermore, DHTM out-

performs LoTM by 0.67%, but trails ToMe

OT S

and

ToMe

w/train

by 0.07% and 0.37% respectively.

These results demonstrate that DHTM outper-

forms most off-the-shelf methods except for ToMe on

DeiT-Base and most training-dependent algorithms,

where it trails slightly behind ToMe

w/train

. This mi-

nor gap is offset by DHTM’s advantage of requiring

no additional training.

4.5 Ablation Study

To validate the merging decision in DHTM, we as-

sess how well the cosine similarity-based merging

compares to random merging of token candidates.

Figure 4 demonstrates that our similarity-based to-

ken merging method preserves higher accuracy than

random merging at equivalent FLOPs levels for both

DHTM. Speciﬁcally, similarity-based merging con-

sistently outperforms random merging, given all the

conﬁgurations of k. For example, DHTM achieves

79.01% accuracy at 2.9 GFLOPs, whereas random

merging achieves only 75.87%.

5 CONCLUSION

We introduced DHTM, an off-the-shelf dynamic to-

ken merging strategy that uses cosine similarity as the

basis for merging decisions. Unlike existing methods

that rely on a ﬁxed centroid token, i.e., reference to-

kens to merge around, or constrain merging within a

limited window, our approach iteratively aggregates

spatially adjacent tokens by evaluating all neighbors

of each token and selecting the most similar pair to

merge in each step. This process progressively ex-

pands regions of similar tokens, effectively reducing

computational overhead.

We designed the model based on two main intu-

itions: ﬁrst, that merging decisions should prioritize

spatially adjacent tokens, as these are more likely to

convey similar information, corresponding visually to

nearby patches. Second, our approach evaluates all

spatially close token-merging candidates, iteratively

selecting the most similar pairs. This removes the

spatial restrictions imposed by some of the previous

methods, allowing for a more ﬂexible and compre-

hensive aggregation process, while relying on adja-

cent tokens. Our approach demonstrates minimal in-

formation loss compared to existing state-of-the-art

methods on the ImageNet-1K dataset and achieves su-

perior performance over most of these methods.

As a perspective, DHTM could be made even

more ﬂexible by enabling variable merging layerwise,

with a threshold imposed on similarity instead of a

ﬁxed number of k merges per layer. Besides, the

approach can be extended to dense prediction tasks,

such as semantic segmentation and object detection,

where token merging can enhance model efﬁciency

and performance, particularly given the high com-

plexity demands of these tasks.

REFERENCES

Bolya, D., Fu, C.-Y., Dai, X., Zhang, P., Feichtenhofer, C.,

and Hoffman, J. (2023). Token merging: Your vit but

faster. In The Eleventh International Conference on

Learning Representations.

Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov,

A., and Zagoruyko, S. (2020). End-to-end object de-

Dynamic Hierarchical Token Merging for Vision Transformers

683

tection with transformers. In European conference on

computer vision, pages 213–229. Springer.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-

Fei, L. (2009). Imagenet: A large-scale hierarchical

image database. In 2009 IEEE conference on com-

puter vision and pattern recognition, pages 248–255.

Ieee.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., et al. (2020). An image is

worth 16x16 words: Transformers for image recogni-

tion at scale. arXiv preprint arXiv:2010.11929.

Haroun, K., Martinet, J., Ben Chehida, K., and Allenet, T.

(2024). Leveraging local similarity for token merg-

ing in Vision Transformers. In ICONIP 2024 - 31th

International Conference on Neural Information Pro-

cessing, Auckland, New Zealand.

Haurum, J. B., Madadi, M., Escalera, S., and Moeslund,

T. B. (2022). Multi-scale hybrid vision transformer

and sinkhorn tokenizer for sewer defect classiﬁcation.

Automation in Construction, 144:104614.

Liu, Y., Gehrig, M., Messikommer, N., Cannici, M., and

Scaramuzza, D. (2024). Revisiting token pruning

for object detection and instance segmentation. In

2024 IEEE/CVF Winter Conference on Applications

of Computer Vision (WACV), pages 2646–2656, Los

Alamitos, CA, USA. IEEE Computer Society.

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin,

S., and Guo, B. (2021). Swin transformer: Hierar-

chical vision transformer using shifted windows. In

Proceedings of the IEEE/CVF international confer-

ence on computer vision, pages 10012–10022.

Marin, D., Chang, J.-H. R., Ranjan, A., Prabhu, A., Raste-

gari, M., and Tuzel, O. (2023). Token pooling in vi-

sion transformers for image classiﬁcation. In Proceed-

ings of the IEEE/CVF Winter Conference on Applica-

tions of Computer Vision, pages 12–21.

Renggli, C., Pinto, A. S., Houlsby, N., Mustafa, B.,

Puigcerver, J., and Riquelme, C. (2022). Learning to

merge tokens in vision transformers. arXiv preprint

arXiv:2202.12015.

Strudel, R., Garcia, R., Laptev, I., and Schmid, C. (2021).

Segmenter: Transformer for semantic segmentation.

In Proceedings of the IEEE/CVF international con-

ference on computer vision, pages 7262–7272.

Touvron, H., Cord, M., Douze, M., Massa, F., Sablayrolles,

A., and J

egou, H. (2021). Training data-efﬁcient im-

age transformers & distillation through attention. In

International conference on machine learning, pages

10347–10357. PMLR.

Ward Jr, J. H. (1963). Hierarchical grouping to optimize an

objective function. Journal of the American statistical

association, 58(301):236–244.

Zeng, W., Jin, S., Liu, W., Qian, C., Luo, P., Ouyang,

W., and Wang, X. (2022). Not all tokens are equal:

Human-centric visual analysis via token clustering

transformer. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 11101–11111.

Zhang, B., Tian, Z., Tang, Q., Chu, X., Wei, X., Shen, C.,

and Liu, Y. (2022). Segvit: Semantic segmentation

with plain vision transformers. NeurIPS.

Zong, Z., Li, K., Song, G., Wang, Y., Qiao, Y., Leng, B.,

and Liu, Y. (2022). Self-slimmed vision transformer.

In European Conference on Computer Vision, pages

432–448. Springer.

VISAPP 2025 - 20th International Conference on Computer Vision Theory and Applications

684