Author Beta-Liouville Multinomial Allocation Model
Faiza Tahsin
a
, Hafsa Ennajari
b
and Nizar Bouguila
c
Concordia Institute for Information Systems Engineering (CIISE), Concordia University, Montreal, Canada
Keywords:
Beta-Liouville, Bayesian Inference, Topic Modeling, Sparsity, Hierarchical Modeling.
Abstract:
Conventional topic models usually presume that topics are evenly distributed among documents. Sometimes,
this presumption may not be true for many real-world datasets characterized by sparse topic representation.
In this paper, we present the Author Beta-Liouville Multinomial Allocation Model (ABLiMA), an innovative
approach to topic modeling that incorporates the Beta-Liouville distribution to better capture the variability
and sparsity of topic presence across documents. In addition to the prior flexibility our model also leverages
the authorship information, leading to more coherent topic diversity.ABLiMA can represent topics that may
be entirely absent or only partially present in specific documents, offering enhanced flexibility and a more
realistic depiction of topic proportions in sparse datasets. Experimental results on the 20 Newsgroups and
NIPS datasets demonstrate superior performance of ABLiMA compared to conventional models, suggesting
its ability to model complex topics in various textual corpora. This model is particularly advantageous for
analyzing text with uneven topic distributions, such as social media or short-form content, where conventional
assumptions often fall short.
1 INTRODUCTION
The rapidly expanding field of text analytics has made
topic modeling a vital technique, enabling the ex-
traction of thematic structures from vast text cor-
pora. Conventional models, such Latent Dirichlet Al-
location (LDA) (Blei et al., 2003), have improved
the understanding of latent topics in texts by claim-
ing that each document comprises a fixed number of
topics. Nonetheless, fixed attributes and shortcom-
ings of these models to tackle topic scarcity and the
fluctuating relevance of topics across documents pro-
vide significant challenges, particularly in the analy-
sis of social media and other forms of dynamic tex-
tual data. Recent improvements in probabilistic topic
modeling seek to address these limitations by us-
ing more flexible distributions that more accurately
represent the complex structure of real-world tex-
tual data (Bouguila, 2009). In this context, we pro-
pose the Author Beta-Liouville Multinomial Alloca-
tion (ABLiMA) model, which integrates the Beta-
Liouville distribution (Epaillard and Bouguila, 2016;
Ali and Bouguila, 2019; Zamzami and Bouguila,
2020) to provide an advanced approach to topic mod-
a
https://orcid.org/0009-0009-6156-1278
b
https://orcid.org/0000-0001-8725-2638
c
https://orcid.org/0000-0001-7224-7940
eling. This model outperforms traditional frameworks
by allowing topic proportions to be less than one,
hence offering a more precise representation of topic
absence and sparsity, a common feature in many cur-
rent datasets.
In addition to flexibly modeling topic propor-
tions, ABLiMA incorporates the influence of author-
specific factors on topic distribution throughout the
modeling process. It emphasizes that authors may
possess distinct topic perspectives that strongly influ-
ence the content. This attribute is essential in contexts
where the author’s identity impacts the material, such
as academic literature, journalistic articles, and espe-
cially in social media, where personal expression and
individual differences are significant. The incorpo-
ration of the Beta-Liouville distribution in ABLiMA
addresses the absence of topics and allows for a more
flexible response to varying levels of author engage-
ment with specific topics. This capability is partic-
ularly beneficial for datasets with high diversity. It
enables the model to competently manage the differ-
ent distributions of topics across texts, leading to im-
proved precision compared to conventional models.
Our contributions in this paper are as follows:
• We introduce the ABLiMA model, a novel ap-
proach to author-topic modeling that integrates
the Beta-Liouville distribution, enabling more
Tahsin, F., Ennajari, H. and Bouguila, N.
Author Beta-Liouville Multinomial Allocation Model.
DOI: 10.5220/0013288000003929
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 27th International Conference on Enterpr ise Information Systems (ICEIS 2025) - Volume 1, pages 251-258
ISBN: 978-989-758-749-8; ISSN: 2184-4992
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
251

flexible and accurate representation of topic dis-
tributions.
• We showcase the effectiveness of Beta-Liouville
priors in capturing the complex dynamics of the-
matic structures and author-specific preferences,
efficiently addressing challenges related to spar-
sity and thematic diversity.
• Through comprehensive experiments on the 20
Newsgroups and NIPS datasets, we demonstrate
that the ABLiMA model outperforms traditional
models like LDA, achieving higher semantic co-
herence.
• We present thorough analyses showing that
ABLiMA surpasses existing models in effectively
capturing the thematic focus of authors, particu-
larly in cases with significant topic variability and
sparsity.
The structure of the paper is as follows: Section 2 pro-
vides an overview of the relevant literature on topic
modeling and the Beta-Liouville distribution. Section
3 outlines the ABLiMA model, covering its genera-
tive process and mathematical formulation. Section 4
presents the experimental results obtained from vari-
ous datasets, and Section 5 concludes with a discus-
sion of findings and future research opportunities.
2 RELATED WORKS
In recent years, topic modeling has been receiving
considerable attention, particularly due to the growth
of probabilistic models such as Latent Dirichlet Al-
location (LDA) (Blei et al., 2003). Documents are
assumed to be mixtures of topics, and topics are as-
sumed to be mixtures of words. Consequently, LDA
has been frequently used for understanding latent the-
matic structures in text corpora. Although LDA has
demonstrated usefulness in numerous applications, it
encounters hardship in capturing sparsity and varia-
tions in thematic relevance across documents, espe-
cially with datasets with short or noisy texts, such as
user-generated content and social media posts. (Blei
and Lafferty, 2007) introduced correlated topic mod-
els to accommodate inter-topic dependencies; how-
ever, sparsity continued to be an obstacle. (Rosen-
Zvi et al., 2004) introduced the Author-Topic Model
(ATM), which builds upon LDA. This model inte-
grates authorship information into the generative pro-
cess, enabling it to identify topics based on both the
authors of the documents and the text they contain.
ATM presumes that an author is associated with a dis-
tribution of topics, and this distribution influences the
documents they write. Sparse data and the varying
importance of topics across various documents and
authors were also challenges that ATM encountered,
despite its advancements.
Several breakthroughs have been made by incor-
porating more flexible distributions to resolve these
limitations. (Bouguila, 2012) introduced infinite Li-
ouville mixture models to enhance text and texture
categorization. The Beta-Liouville distribution has
been implemented in numerous domains, such as
high-dimensional data modeling and text clustering
(Fan and Bouguila, 2013a). The Beta-Liouville distri-
bution has demonstrated potential in handling sparsity
and skewness in datasets, which are frequent chal-
lenges in real-world data, such as text corpora. (Fan
and Bouguila, 2013b) Also proposed an approach for
online learning using a Dirichlet process mixture of
Beta-Liouville distributions.
(Fan and Bouguila, 2015; Luo et al., 2023) illus-
trated the Beta-Liouville distribution’s efficiency in
the context of document clustering and proportional
data modeling when dealing with scarce and skewed
data. This distribution is an appropriate choice for
advanced topic modeling frameworks due to its abil-
ity to model intricate relationships among latent vari-
ables. (Bakhtiari and Bouguila, 2014) also introduced
an online learning variant of topic models that uti-
lizes Beta-Liouville priors, which allows for real-time
changes to topic distributions. This online approach
is appropriate to the requirements of contemporary
dynamic datasets, including social media feeds and
news articles, with thematic relevance that fluctuates
over time. (Bakhtiari and Bouguila, 2016) introduced
the Latent Beta-Liouville Allocation Model, which
extends conventional topic modeling frameworks by
incorporating Beta-Liouville priors to capture latent
structure in count data. This model was recently
proposed. This model demonstrated substantial en-
hancements in terms of interpretability and accuracy
in high-dimensional and text datasets.
The ABLiMA model enhances these develop-
ments by incorporating Beta-Liouville priors into
the author-topic modeling framework. In doing so,
ABLiMA enhances previous models by addressing
the challenge of sparsity and varying thematic rel-
evance in author-specific documents. In summary,
ABLiMA is a product of both classical models, such
as LDA, and contemporary developments in the ap-
plication of flexible priors, such as the Beta-Liouville
distribution. With a combination of these ideas, the
ABLiMA gives a far superior and more versatile ap-
proach to author-topic modeling that is capable of
handling the present-day textual data set.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
252

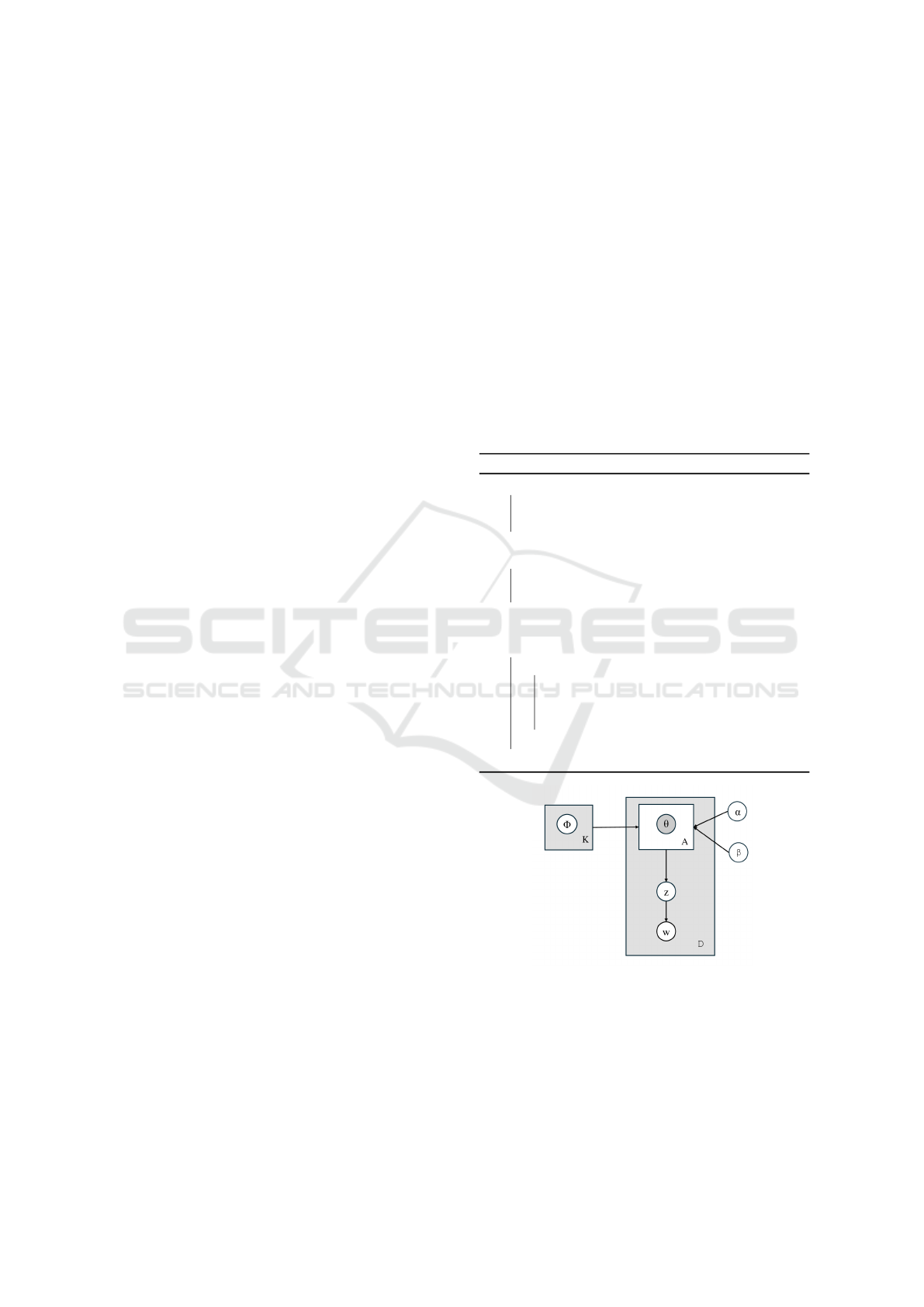
3 PROPOSED MODEL
In this section, we present the proposed Author Beta-
Liouville Multinomial Allocation (ABLiMA) model,
describing its generative process, parameter infer-
ence, and hyperparameter optimization. In order to
flexibly represent author-specific topic distributions,
we first define the generative process of ABLiMA,
which uses the Beta-Liouville distribution. This is
followed by a breakdown of the Gibbs sampling
method for parameter inference, which makes it feasi-
ble to estimate latent variables effectively. Lastly, we
discuss the techniques for optimizing hyperparame-
ters to enhance the model’s performance.
3.1 Model Definition
The Author Beta-Liouville Multinomial Allocation
ABLiMA model is an advanced author-topic model
that uses the Beta-Liouville distribution for modeling
author-specific topic distributions and a Dirichlet dis-
tribution for topic-word distributions.
3.1.1 Generative Process
The generative process of the ABLiMA model in-
volves the following steps:
• Author-Level Topic Proportions: For each author
a ∈ {1, ..., A}, we draw the author-level topic
proportions from a Beta-Liouville distribution pa-
rameterized by vectors
⃗
α and
⃗
β. This models the
variability and sparsity in author-specific thematic
focus.
θ
a
∼ Beta-Liouville(
⃗
α,
⃗
β)
Here, θ
a
is a vector representing the proportion of
different topics for author a. The Beta-Liouville
distribution provides greater flexibility than the
standard Dirichlet distribution by allowing more
diverse topic proportion patterns.
• Topic-Word Distribution: For each topic k ∈
{1,. .. ,K}, draw a topic-word distribution φ
k
from
a Dirichlet distribution parameterized by β. This
distribution ensures that each topic is associated
with a distinct distribution over words.
φ
k
∼ Dirichlet(β)
Here, φ
k
represents the probability distribution
over words for topic k.
• Document-Level Topic Assignment and Word
Generation For each document d ∈ {1, .. ., D} au-
thored by an author a, and for each word position
n ∈ {1,. .. ,N
d
}:
– A topic z
d,n
is drawn for the n-th word from the
author’s topic distribution θ
a
:
z
d,n
∼ Multinomial(θ
a
)
This step assigns a topic to each word in a doc-
ument based on the thematic focus of the docu-
ment’s author.
– The word w
d,n
is drawn from the topic-word
distribution φ
z
d,n
:
w
d,n
∼ Multinomial(φ
z
d,n
)
This step generates the word based on the topic
assigned in the previous step.
We have outlined the generative process of
ABLiMA in the algorithm provided below:
Algorithm 1: Generative Process of the ABLiMA Model.
for each author a ∈ {1, . . . , A} do
Draw author-level topic proportions
θ
a
∼ Beta-Liouville(
⃗
α,
⃗
β);
end
for each topic k ∈ {1, .. ., K} do
Draw topic-word distribution
φ
k
∼ Dirichlet(β);
end
for each document d ∈ {1, .. ., D} authored
by author a do
for each word position n ∈ {1, . . . ,N
d
} do
Draw topic z
d,n
∼ Multinomial(θ
a
);
Draw word
w
d,n
∼ Multinomial(φ
z
d,n
);
end
end
Figure 1: Graphical Model of ABLiMA.
3.2 Parameter Inference
To estimate the hidden parameters of the Author Beta-
Liouville Multinomial Allocation (ABLiMA) model,
we utilize a Gibbs Sampling approach (Griffiths and
Steyvers, 2004), which is a Markov Chain Monte
Carlo (MCMC) method that allows efficient inference
Author Beta-Liouville Multinomial Allocation Model
253

Table 1: Summary of Mathematical Notations.
Notation Meaning
φ
k
The word distribution for topic k.
a,b Parameters of the Beta-Liouville distri-
bution for the word distribution within
topic k.
θ
a
The topic distribution for author a.
⃗
α,
⃗
β Hyperparameters for the Beta-Liouville
distribution for author-level topic pro-
portions.
z
d,n
The topic assigned to the n-th word in
document d.
w
d,n
The n-th word in document d.
A The number of authors in the dataset.
k The number of topics in the model.
d The number of documents in the
dataset.
N
d
The number of words in document d.
of the posterior distributions for complex probabilis-
tic models. The latent parameters that need to be in-
ferred in ABLIMA include the author-level topic pro-
portions (θ
a
), the topic-word distributions (φ
k
), and
the topic assignments for each word in each document
(z
d,n
). Below, we describe how each of these compo-
nents is inferred iteratively.
The Beta-Liouville distribution, defined over a K-
dimensional simplex, is characterized by the param-
eter vector θ = (θ
1
,θ
2
,. .. ,θ
K
), subject to the con-
straint
∑
K
k=1
θ
k
= 1. It is complemented by the hyper-
parameter vector δ = (α
1
,α
2
,. .. ,α
K
,α, γ), providing
precise control over the distribution’s shape and scale.
The probability density function is given by (Fan
and Bouguila, 2013a):
p(θ | δ) =
Γ

∑
K−1
k=1
α
k

Γ(α + γ)
Γ(α)Γ(γ)
∏
K−1
k=1
Γ(α
k
)
×
K−1
∏
k=1
θ
α
k
−1
k
K−1
∑
k=1
θ
k
!
α−
∑
K−1
k=1
α
k
× 1 −
K−1
∑
k=1
θ
k
!
γ−1
(1)
where Γ(·) represents the Gamma function.
Here is the joint probability density function for
ABLiMA:
p(θ
a
,φ
k
,Z,W |
⃗
α,
⃗
β,a, b) =
A
∏
a=1
p(θ
a
|
⃗
α,
⃗
β)
K
∏
k=1
p(φ
k
| a,b)
D
∏
d=1
p(Z
d
| θ
a
)p(W
d
| φ
Z
d
),
(2)
The Gibbs Sampling function is given by:
p(z
d,n
= k | z
−d,n
,w,
⃗
α,
⃗
β,a, b) ∝ (θ
a,k
+ α
k
− 1)
· (φ
k,w
d,n
+ b
w
d,n
− 1)
(3)
To optimize the hyperparameters, we use a Monte
Carlo Expectation-Maximization (MCEM) approach.
The goal of MCEM is to iteratively refine the hy-
perparameters in such a way that they maximize the
likelihood of the observed data.The MCEM process
consists of two main steps: the E-step (Expectation)
and the M-step (Maximization). In the E-step, we use
Gibbs Sampling to approximate the latent variables.
For each word in a document, we draw topic assign-
ments based on the conditional distributions. These
topic assignments provide estimates for the hidden
topic structure in the corpus. By repeating the Gibbs
Sampling procedure for a sufficiently large number
of iterations, we approximate the expected value of
the latent variables given the current set of hyperpa-
rameters. In the M-step, we maximize the expected
complete-data likelihood of the training documents
with respect to the hyperparameters. Specifically, we
find the values of the hyperparameters (
⃗
α,
⃗
β, a, and
b) that maximize the joint likelihood of the data and
the topic assignments. For the Beta-Liouville author-
level topic distribution hyperparameters (
⃗
α and
⃗
β) For
the Beta-Liouville word distribution hyperparameters
(a and b), we optimize them by maximizing the like-
lihood of the observed word distributions for each
topic. The objective in the M-step is to maximize the
complete-data likelihood:
p(w,z |
⃗
α,
⃗
β,a, b) = p(w | z, a, b) p(z |
⃗
α,
⃗
β)
where:
• p(w | z, a,b) represents the probability of words
given the topic assignments.
• p(z |
⃗
α,
⃗
β) represents the probability of the topic
assignments given the author-level topic propor-
tions.
To optimize the hyperparameters, we solve the
following optimization problem for
⃗
α,
⃗
β, a, and b:
(
⃗
α
∗
,
⃗
β
∗
,a
∗
,b
∗
) = arg max
⃗
α,
⃗
β,a,b
E
z∼p(z|w,
⃗
α,
⃗
β,a,b)
h
log p(w, z |
⃗
α,
⃗
β,a, b)
i
where E represents the expectation over the latent
variables z drawn from the conditional distribution
p(z | w,
⃗
α,
⃗
β,a, b).
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
254

Algorithm 2: Monte Carlo EM for ABLiMA Hyperparam-
eter Optimization.
Data: Training corpus, initial
hyperparameters
⃗
α,
⃗
β, and topic
assignments Z
Result: Optimized hyperparameters
⃗
α
∗
,
⃗
β
∗
Initialization: Set initial values for α, β, and
topic assignments Z;
repeat
E-Step: Gibbs Sampling ;
Perform Gibbs sampling to update the
topic assignments Z;
M-Step: Hyperparameter
Maximization ;
Maximize the likelihood p(W,Z |
⃗
α,
⃗
β)
with respect to
⃗
α and
⃗
β;
Update
⃗
α and
⃗
β based on the expected
topic assignments Z;
until convergence of
⃗
α,
⃗
β;
Return optimized hyperparameters
⃗
α
∗
,
⃗
β
∗
The specific form of the expectation in the E-step:
E
z
"
K
∑
k=1
V
∑
w=1
C
k,w
logφ
k,w
+
A
∑
a=1
K
∑
k=1
C
a,k
logθ
a,k
#
,
where the counts C
k,w
and C
a,k
are approximated us-
ing Gibbs Sampling. These terms represent the ex-
pected contribution of the current topic and author
assignments to the overall likelihood of the observed
data, given the current hyperparameters.
4 EXPERIMENTAL RESULTS
4.1 Datasets
• 20 Newsgroups: This dataset contains documents
from 20 different newsgroups, representing a
wide variety of topics. It is commonly used for
evaluating topic modeling techniques.
• NIPS Conference Papers: This dataset includes
papers from NIPS conference, covering a diverse
range of topics in machine learning. It is suited to
evaluate how a topic modeling approach can cap-
ture author-specific topics.
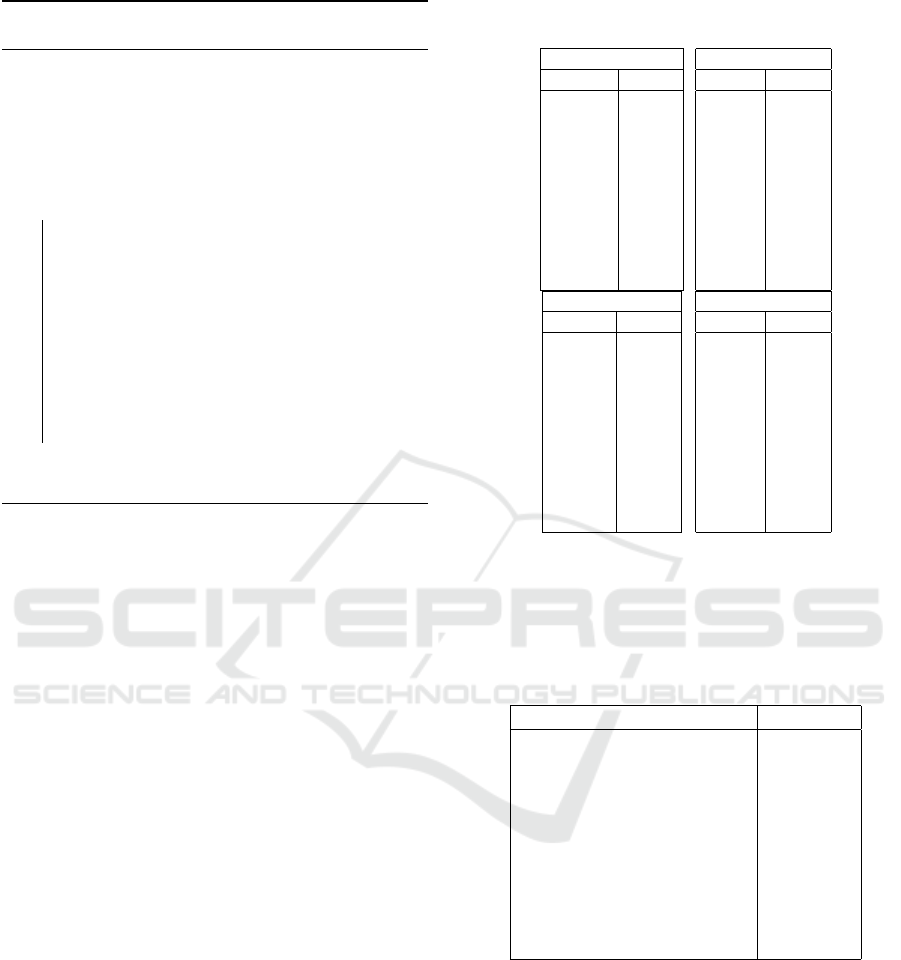
Table 2 shows the word probabilities for selected top-
ics, where the most probable words are displayed
for six representative topics. The probability of
each word indicates its significance within a partic-
ular topic, helping to understand the semantic focus
Table 2: ABLiMA-Word Probabilities per Topic on 20
newsgroups dataset.
TOPIC 6
WORD PROB.
God 0.0167
Christian 0.0111
Jesus 0.0086
Bible 0.0080
Believe 0.0066
Christ 0.0064
Church 0.0063
Life 0.0055
People 0.0055
Word 0.0052
TOPIC 7
WORD PROB.
Game 0.0181
Team 0.0152
Play 0.0116
Player 0.0105
Year 0.0105
Win 0.0082
Season 0.0080
League 0.0072
Score 0.0062
Fan 0.0060
TOPIC 10
WORD PROB.
Space 0.0164
Launch 0.0077
Earth 0.0073
NASA 0.0071
Year 0.0068
Orbit 0.0066
Data 0.0059
Program 0.0055
Project 0.0055
Large 0.0054
TOPIC 12
WORD PROB.
Work 0.0102
Power 0.0094
Good 0.0069
Signal 0.0067
Design 0.0063
Wire 0.0062
Current 0.0061
Radio 0.0061
Device 0.0061
Low 0.0060
of each topic. For instance, ”Topic 6” is centered
around religion-related terms, while ”Topic 7” rep-
resents sports, evidenced by terms like ”Game” and
”Team”. Table 3 illustrates the author-topic distribu-
Table 3: ABLiMA-Author-Topic Distribution on 20 News-
groups dataset.
Author Topics
[e-mail] 3, 15, 2
[e-mail] 5, 8, 15
[e-mail] 19, 18, 1
jgreen@amber 11, 19, 8
[e-mail] 0, 1, 5
mathew 15, 8, 5
[e-mail] 10, 1, 15
[e-mail] 3, 17, 1
[e-mail] 11, 19, 15
[e-mail] 10, 19, 8
tions, showing each author’s association with a set of
topics that represent the subjects they most frequently
address. For example, Irwin Arnstein is primarily as-
sociated with topics 3, 15, and 2, suggesting a diverse
thematic focus across different subject areas. This ta-
ble illustrates the connection between authors and the
dominant themes in their writing. The above tables
present the results of the topic analysis conducted on
the NIPS dataset. Table 4 provides word probabilities
for different topics, indicating the most representative
words for each topic. For instance, Topic 2 primarily
relates to nodes, graphs, and groups, suggesting a fo-
Author Beta-Liouville Multinomial Allocation Model
255

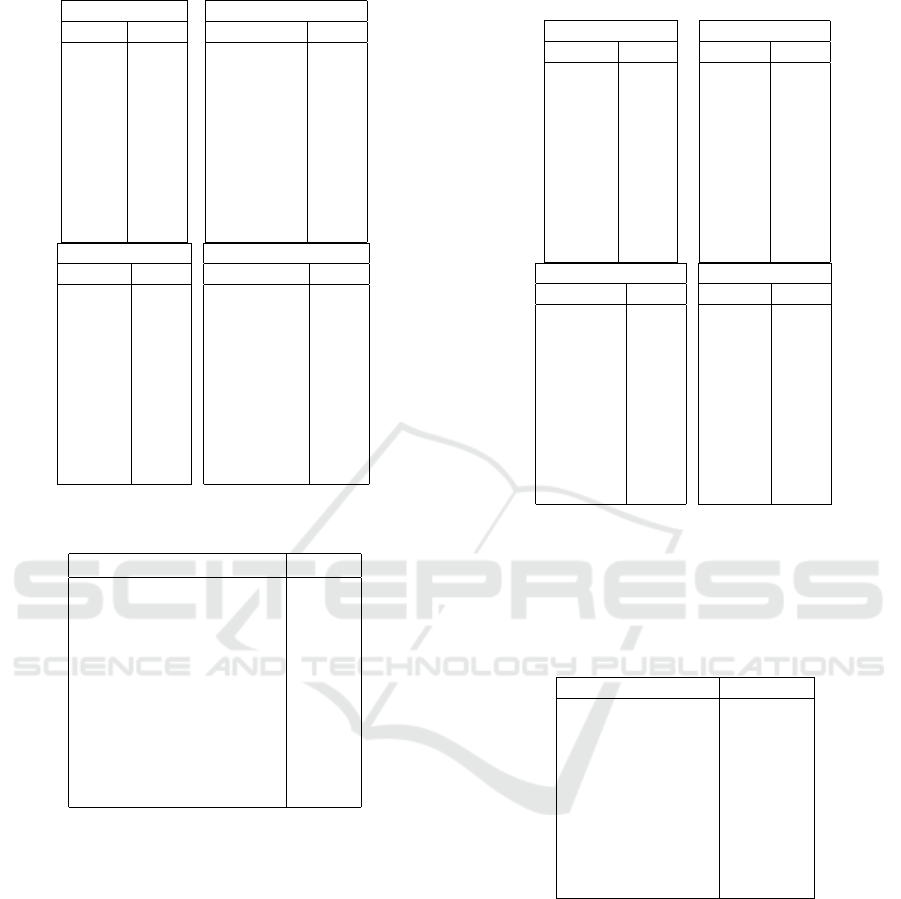
Table 4: ABLiMA-Word Probabilities per Topic on NIPS.
TOPIC 2
WORD PROB.
Node 0.0043
Binary 0.0039
Graph 0.0038
Assign 0.0038
Group 0.0036
Edge 0.0035
Capture 0.0033
Identify 0.0032
Connect 0.0032
Partition 0.0029
TOPIC 3
WORD PROB.
Layer 0.0057
Architecture 0.0055
Deep 0.0054
Bengio 0.0052
Hinton 0.0051
Convolutional 0.0043
Sutskever 0.0041
Unit 0.0039
Activation 0.0035
Lecun 0.0034
TOPIC 5
WORD PROB.
IID 0.0040
Sense 0.0034
Family 0.0033
Finite 0.0033
Uniform 0.0031
Turn 0.0031
Literature 0.0029
Establish 0.0029
Implies 0.0029
Distance 0.0028
TOPIC 6
WORD PROB.
Convex 0.0076
Descent 0.0062
Minimization 0.0057
Norm 0.0049
Regularization 0.0045
Dual 0.0044
Convexity 0.0043
Smooth 0.0040
Regularize 0.0039
Program 0.0038
Table 5: ABLiMA-Author-Topic Distribution in NIPS
dataset.
Author Topics
Xiangyu Wang 3, 4, 6
Fangjian Guo 9, 8, 7
Lars Buesing 3, 0, 2
David Silver 0, 8, 3
Daan Wierstra 9, 8, 7
Nicolas Heess 3, 2, 0
Oriol Vinyals 2, 0, 7
Razvan Pascanu 2, 7, 3
Danilo Jimenez Rezende 3, 2, 0
Theophane Weber 9, 8, 7
cus on network structures. Topic 3 contains terms like
”layer” and ”deep,” indicating a focus on deep learn-
ing and neural network architecture. Table 5 shows
the topic distributions for various authors in the NIPS
dataset. For example, Xiangyu Wang is most asso-
ciated with topics 3, 4, and 6, reflecting a combina-
tion of interests that could include deep learning, opti-
mization, and related fields. These tables collectively
illustrate the thematic preferences of both the topics
and the authors, providing insights into their research
focus areas.
Table 6 shows the word probabilities across sev-
eral topics for in the 20 Newsgroups for ATM
(Author-Topic model). In Topic 1, high-probability
words such as News, Reuters, and Trump suggest a
focus on current events, media, and political figures,
with additional emphasis on financial terms like Mar-
Table 6: ATM-Word Probabilities per Topic on 20 News-
groups dataset.
TOPIC 1
WORD PROB.
News 0.032
Reuters 0.016
Trump 0.010
Business 0.008
World 0.008
Percent 0.007
State 0.007
Market 0.007
President 0.006
Company 0.006
TOPIC 2
WORD PROB.
President 0.010
Trump 0.008
Year 0.007
New 0.007
House 0.006
State 0.006
Time 0.005
City 0.005
Officials 0.005
Include 0.005
TOPIC 4
WORD PROB.
Trump 0.0037
State 0.0012
President 0.0011
Clinton 0.007
Campaign 0.006
Vote 0.006
Republican 0.006
Party 0.005
House 0.005
Republicans 0.005
TOPIC 9
WORD PROB.
Super 0.000
Like 0.000
Peak 0.000
New 0.000
Time 0.000
Play 0.000
Facebook 0.000
Learn 0.000
Company 0.000
Story 0.000
ket and Company. Topic 2 continues with political
themes, with words like President, Trump, and House
indicating government and public administration dis-
cussions. Table 7 displays the distribution of author
Table 7: ATM-Author Topics Distribution on 20 News-
groups dataset.
Author Topics
Atlantic 1, 4, 18
Breibart 1, 4, 18
Business Insider 1, 2, 4, 18
Buzzfeed News 1, 2, 4, 18
CNN 2, 4, 18
Fox News 1, 2, 4, 18
Los Angeles Times 2, 18
NPR 1, 2, 4, 18
New York Post 2, 4, 18
New York Times 2, 4, 18
topics within the 20 Newsgroups dataset. It shows
that many prominent news outlets, such as Atlantic,
Breitbart, and Fox News, frequently cover Topics 1,
4, and 18, indicating shared themes or areas of focus
among these sources. Other publications like CNN,
New York Post, and New York Times have significant
coverage of Topics 2, 4, and 18, reflecting a possi-
ble emphasis on political and current events. Table 8
outlines the LDA word probabilities for several top-
ics in the 20 Newsgroups. In Topic 1, terms such as
Image, File, and Jpeg suggest discussions related to
digital media and file handling, with frequent refer-
ences to files and images. Topic 2 features words like
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
256

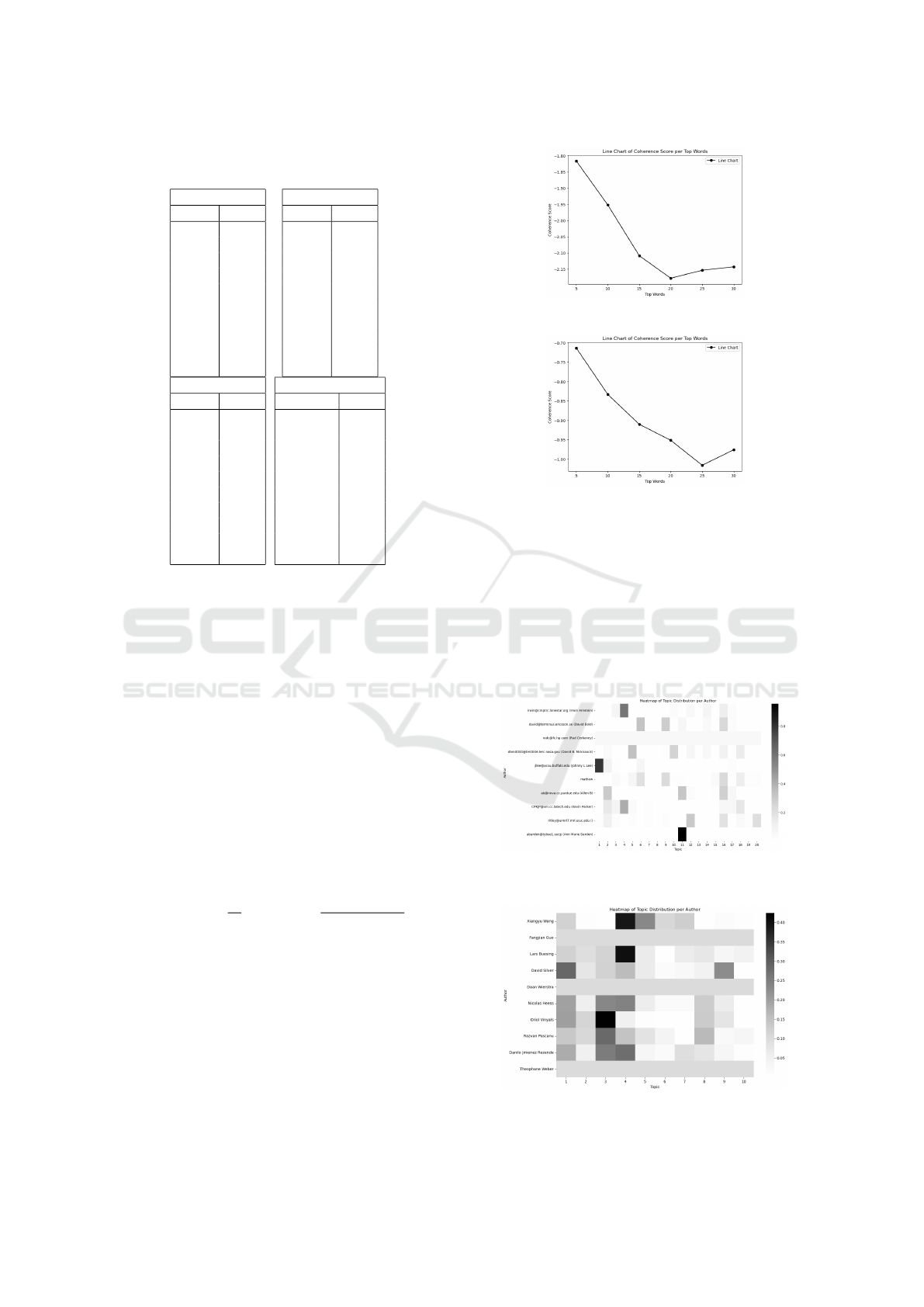
Table 8: LDA- Word Probabilities per Topic on 20 News-
groups dataset.
TOPIC 1
WORD PROB.
Image 0.017
File 0.011
Use 0.010
Bike 0.010
Know 0.006
Good 0.006
Like 0.005
Email 0.005
Jpeg 0.005
Just 0.005
TOPIC 2
WORD PROB.
Gun 0.012
File 0.011
Use 0.011
Make 0.008
Know 0.008
Like 0.008
Say 0.008
Right 0.007
Dod 0.006
Just 0.006
TOPIC 4
WORD PROB.
Need 0.009
Use 0.008
Gun 0.007
State 0.007
Like 0.007
Dod 0.006
Apr 0.006
File 0.006
Say 0.006
Make 0.005
TOPIC 6
WORD PROB.
Say 0.008
Fbi 0.008
Child 0.008
Compound 0.007
Make 0.007
Batf 0.006
Come 0.006
Start 0.005
Roby 0.005
Day 0.005
Gun, File, and Right, indicating a focus on rights and
possibly legal or policy-related content.
4.2 Coherence Score
Topic coherence measures the quality of topics gen-
erated by a model, reflecting how interpretable and
meaningful the topics are to human readers. It quan-
tifies the semantic similarity between the most repre-
sentative words in a topic, aiming to determine if the
words typically occur together in real-world contexts.
A high coherence score indicates that the generated
topics consist of related words, making them easier
to interpret and understand. This metric is crucial for
evaluating the effectiveness of topic models, as it en-
sures the topics extracted are insightful and relevant
to the underlying dataset (Ennajari et al., 2021):
Coherence =
1
M
N
∑
i=2
i−1
∑
j=1
log

D(w
i
,w
j
) + 1
D(w
j
)

Figures 2 and 3 illustrate the coherence scores of top-
ics derived from the ABLiMA model, as the num-
ber of top words used for coherence calculation in-
creases from 5 to 30. The first chart corresponds to
the 20 Newsgroups dataset, while the second chart
represents the NIPS dataset. For both datasets, we ob-
serve a general trend of decreasing coherence scores
as the number of top words grows, indicating di-
minishing coherence between the additional words.
The coherence scores of the ABLiMA model were
Figure 2: Coherence Score of 20 Newsgroups dataset.
Figure 3: Coherence Score of NIPS dataset.
computed following the methodology described by
(Mimno et al., 2012), which has been shown to ef-
fectively reflect the semantic consistency of topics.
4.3 Qualitative Analysis
The qualitative analysis is done by manual inspection.
(Chang et al., 2009) explored how well humans can
interpret the output of topic models. The heatmaps
Figure 4: Coherence Score of NIPS dataset.
Figure 5: Coherence Score of NIPS dataset.
Author Beta-Liouville Multinomial Allocation Model
257

in figure 4 and 5 above show the topic distributions
for authors in the two datasets: 20 Newsgroups and
NIPS. Each row represents an author, while each col-
umn corresponds to a topic. The intensity of the color
indicates the strength of association between the au-
thor and the respective topic. In the 20 Newsgroups
dataset, we see some authors strongly aligned with
particular topics, as indicated by the darker shades.
Similarly, the NIPS dataset heatmap reveals vary-
ing topic preferences among the authors, showcasing
some strong associations to specific topics, especially
by authors such as Oriol Vinyals and Fangjian Guo.
These visualizations help understand the thematic fo-
cus of different authors.
5 CONCLUSION
We proposed ABLiMA, an author-topic modeling ap-
proach, by integrating the Beta-Liouville, allowing
greater flexibility in capturing the variability and spar-
sity of author-specific thematic focus. Through ex-
periments, the model demonstrated its ability to ex-
tract meaningful topic distributions, reflected in co-
herent topic clusters and insightful author-topic rela-
tionships. Visualizations like heatmaps and coherence
scores further validated the effectiveness of the model
in distinguishing distinct topic preferences among au-
thors. Future work could focus on optimizing hy-
perparameter estimation techniques and incorporating
automatic inference of the optimal number of topics
such as Dirichlet Process-based models.
REFERENCES
Ali, S. and Bouguila, N. (2019). Variational learning of
beta-liouville hidden markov models for infrared ac-
tion recognition. In 2019 IEEE/CVF Conference on
Computer Vision and Pattern Recognition Workshops
(CVPRW), pages 898–906.
Bakhtiari, A. S. and Bouguila, N. (2014). Online learning
for two novel latent topic models. In Linawati, Ma-
hendra, M. S., Neuhold, E. J., Tjoa, A. M., and You,
I., editors, Information and Communication Technol-
ogy - Second IFIP TC5/8 International Conference,
ICT-EurAsia 2014, Proceedings, volume 8407 of Lec-
ture Notes in Computer Science, pages 286–295, Bali,
Indonesia. Springer.
Bakhtiari, A. S. and Bouguila, N. (2016). A latent beta-
liouville allocation model. Expert Systems with Appli-
cations, 45:260–272.
Blei, D. M. and Lafferty, J. D. (2007). A correlated topic
model of science. The Annals of Applied Statistics,
1:17–35.
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent
dirichlet allocation. Journal of Machine Learning Re-
search, 3(Jan):993–1022.
Bouguila, N. (2009). A model-based approach for discrete
data clustering and feature weighting using map and
stochastic complexity. IEEE Transactions on Knowl-
edge and Data Engineering, 21(12):1649–1664.
Bouguila, N. (2012). Infinite liouville mixture models with
application to text and texture categorization. Pattern
Recognit. Lett., 33(2):103–110.
Chang, J., Gerrish, S., Wang, C., Boyd-Graber, J. L., and
Blei, D. M. (2009). Reading tea leaves: How humans
interpret topic models. In Advances in Neural Infor-
mation Processing Systems (NIPS), pages 288–296.
Ennajari, H., Bouguila, N., and Bentahar, J. (2021). Com-
bining knowledge graph and word embeddings for
spherical topic modeling. IEEE Transactions on
Neural Networks and Learning Systems, 34(7):3609–
3623.
Epaillard, E. and Bouguila, N. (2016). Proportional data
modeling with hidden markov models based on gen-
eralized dirichlet and beta-liouville mixtures applied
to anomaly detection in public areas. Pattern Recog-
nit., 55:125–136.
Fan, W. and Bouguila, N. (2013a). Learning finite beta-
liouville mixture models via variational bayes for pro-
portional data clustering. In Rossi, F., editor, Pro-
ceedings of the 23rd International Joint Conference
on Artificial Intelligence (IJCAI), pages 1323–1329,
Beijing, China. IJCAI/AAAI.
Fan, W. and Bouguila, N. (2013b). Online learning of
a dirichlet process mixture of beta-liouville distri-
butions via variational inference. IEEE Transac-
tions on Neural Networks and Learning Systems,
24(11):1850–1862.
Fan, W. and Bouguila, N. (2015). Expectation propaga-
tion learning of a dirichlet process mixture of beta-
liouville distributions for proportional data cluster-
ing. Engineering Applications of Artificial Intelli-
gence, 43:1–14.
Griffiths, T. L. and Steyvers, M. (2004). Finding scientific
topics. Proceedings of the National Academy of Sci-
ences, 101(suppl 1):5228–5235.
Luo, Z., Amayri, M., Fan, W., and Bouguila, N. (2023).
Cross-collection latent beta-liouville allocation model
training with privacy protection and applications.
Appl. Intell., 53(14):17824–17848.
Mimno, D., Wallach, H. M., Talley, E., Leenders, M., and
McCallum, A. (2012). Optimizing semantic coher-
ence in topic models. In Proceedings of the Confer-
ence on Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 262–272.
Rosen-Zvi, M., Griffiths, T., Steyvers, M., and Smyth, P.
(2004). The author-topic model for authors and doc-
uments. In Proceedings of the 20th Conference on
Uncertainty in Artificial Intelligence, pages 487–494.
Zamzami, N. and Bouguila, N. (2020). High-dimensional
count data clustering based on an exponential approx-
imation to the multinomial beta-liouville distribution.
Inf. Sci., 524:116–135.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
258