Exploring Shared Gaussian Occupancies for Tracking-Free,

Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

Nico Uhlemann

, Melina W

ordehoff

and Markus Lienkamp

Technical University of Munich, School of Engineering & Design, Department of Mobility Systems Engineering, Institute of

Automotive Technology and Munich Institute of Robotics and Machine Intelligence (MIRMI), Germany

{nico.uhlemann, melina.w

ordehoff, lienkamp}@tum.de

Keywords:

Pedestrian Motion Prediction, Gaussian Occupancy, Scene-Centric, Autonomous Driving.

Abstract:

This work introduces a scalable framework for pedestrian motion prediction in urban trafﬁc, tailored for real-

world applications in autonomous driving. Existing methods typically predict either individual objects, cre-

ating challenges with higher agent counts, or rely on discretized occupancy maps, sacriﬁcing precision. To

overcome these limitations, we propose a scene-centric transformer architecture with a cluster-based training

approach, capturing pedestrian dynamics through combined probability distributions. This strategy enhances

prediction efﬁciency as groups of nearby agents are uniﬁed into a shared representation, thus reducing compu-

tational load while still maintaining a continuous output format. Additionally, we investigate a tracking-free

design, exploring the feasibility of accurate predictions based solely on object lists without explicit object as-

sociation. To assess predictive performance, we compare our approach to state-of-the-art trajectory prediction

methods, analyzing several metrics while keeping practical applications in mind. Evaluations on a dedicated

pedestrian benchmark derived from the Argoverse 2 dataset demonstrate the model’s strong predictive accu-

racy and highlight the potential for tracking-free future developments.

1 INTRODUCTION

Autonomous driving has received signiﬁcant attention

in both industry and research due to its potential to en-

hance trafﬁc ﬂow, improve mobility for individuals,

and offer economic beneﬁts (Hussain and Zeadally,

2019). However, integrating autonomous vehicles

(AVs) into complex urban environments presents sub-

stantial challenges, especially in accurately predict-

ing pedestrian motion which is crucial for its safety.

Pedestrians, a particularly vulnerable group of road

users, face a high risk of fatality in accidents and of-

ten exhibit seemingly unpredictable movement pat-

terns as they are unconstrained by predeﬁned lanes or

non-holonomic limitations (Schuetz and Flohr, 2024).

Motion prediction for autonomous driving has

been extensively studied, with deep learning methods

becoming the state of the art. These approaches fall

into two categories: individual trajectory prediction

and environmental occupancy prediction. Trajectory-

based methods assign uni- or multimodal predictions

to each pedestrian (Ridel et al., 2018), requiring accu-

https://orcid.org/0009-0006-8774-7888

https://orcid.org/0009-0009-0553-7265

https://orcid.org/0000-0002-9263-5323

Figure 1: Dense pedestrian crowd crossing the street in

front of the ego vehicle captured by a LiDAR sensor.

rate tracking to model interactions (Uhlemann et al.,

2024). However, tracking becomes challenging in

dense urban settings and for higher agent counts as

seen in Figure 1. In contrast, occupancy-based meth-

ods predict environments holistically, representing

spaces as occupied or unoccupied (Huang et al., 2023)

while often using grid-based formats from a bird’s-

eye-view (BEV) (Rudenko et al., 2021). These meth-

ods face trade-offs between computational efﬁciency

and spatial precision which is determined by the grid

resolution (Luo et al., 2021).

To address these limitations, this paper introduces

a continuous, probabilistic occupancy approach for

pedestrian motion prediction in urban trafﬁc. By

100

Uhlemann, N., Wördehoff, M. and Lienkamp, M.

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving.

DOI: 10.5220/0013288900003941

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 100-112

ISBN: 978-989-758-745-0; ISSN: 2184-495X

leveraging mixture models, our model incorporates

uncertainty and achieves accurate and scalable results

through a compact network. Unlike traditional meth-

ods, we minimizes tracking dependency by directly

processing object lists which offers practical advan-

tages in urban scenarios. To our knowledge, this

continuous probabilistic occupancy framework, com-

bined with a tracking-free variation, is a novel contri-

bution to the ﬁeld yet to be explored. The key contri-

butions of this work are summarized as follows:

• Occupancy Representation: We propose a novel

occupancy representation inspired by mixture

models, using shared probability distributions in-

stead of grid-based methods. By clustering nearby

pedestrians and predicting their motion collec-

tively, our approach reduces computational de-

mands as agent counts increase.

• Model Architecture: We develop a compact,

scene-centric method utilizing a transformer-

based architecture that achieves state-of-the-art

accuracy while being scalable regarding the num-

ber of agents considered.

• Tracking Dependency: Evaluating both,

tracking-dependent and tracking-free approaches,

we showcase that competitive performance can be

achieved without an explicit object association.

2 RELATED WORK

The prediction of pedestrian and vehicle trajectories

in autonomous driving has been widely studied,

with a focus on models that address the inherent

uncertainty in future motion. This section introduces

relevant approaches forming the basis of our pre-

diction framework, complemented by an overview

presented in Figure 2.

Trajectory Prediction. The most common

approach to predict pedestrian motion is through

spatial-temporal paths, called trajectories. Here,

unimodal predictions anticipate a deterministic

outcome, corresponding to the most likely action

(Becker et al., 2019; Zamboni et al., 2022). While

sufﬁcient for slow-moving objects like pedestrians,

particularly for prediction horizons of up to 6 s (Uh-

lemann et al., 2025), more dynamic agents, such as

cyclists and vehicles, require representations capable

of capturing diverse potential futures (Huang et al.,

2022). Multimodal trajectory prediction addresses

this need by assigning each agent a set of trajectories,

often with associated probabilities (Ngiam et al.,

2022; Gilles et al., 2022a) and linked to discrete

actions or maneuvers, such as turning, lane-changing,

or stopping (Lefevre et al., 2014). Generative

models, such as Generative Adversarial Networks

(GANs) and Conditional Variational Autoencoders

(CVAEs), are frequently employed to generate these

representations (Mohamed et al., 2022). GANs use

a generator-discriminator architecture where the

generator proposes candidate trajectories, and the

discriminator evaluates their plausibility against real

data (Goodfellow et al., 2020). Examples include

Social GAN (Gupta et al., 2018) and Social-BIGAT

(Kosaraju et al., 2019), which incorporate social in-

teractions using attention mechanisms or graph-based

structures. CVAEs encode agent positions into a

latent space and decode potential futures (Sohn et al.,

2015). Previous works such as BiTraP (Yao et al.,

2021), ExpertTraj (Zhao and Wildes, 2021), and

AgentFormer (Yuan et al., 2021) demonstrate that

modeling latent variables as Gaussian distributions

reduces false positives compared to non-parametric

distributions. Although generative models effectively

capture complex distributions, they face challenges

such as mode collapse, where predicted trajectories

lack diversity and require extensive sampling, leading

to increased randomness and computational overhead

(Huang et al., 2023; Gilles et al., 2022a).

Non-Parametric Prediction. Probabilistic

re-presentations, such as occupancies, offer a way to

capture the diversity of scenarios beyond trajectories

by predicting the behavior of all objects in a scene

collectively (Toyungyernsub et al., 2022). The

most common non-parametric approach discretizes

the surrounding space into grid cells of equal size

(Gulzar et al., 2021). Although focusing on single

pedestrians, Ridel et al. (Ridel et al., 2020) em-

ploy a Convolutional Long Short-Term Memory

(ConvLSTM) network to predict future occupancies

by assigning binary occupation probabilities to

grid cells at each timestep. Similarly, Lange et al.

(Lange et al., 2021) extend this idea using continuous

probabilities. Jain et al. advance this further with

DRF-Net (Jain et al., 2019), a ResNet-based model

that integrates semantic and dynamic information

into a 3D spatio-temporal tensor. Although precise

tracking is still required, the method exceeds the

previously best performance. As seen with Y-Net

(Mangalam et al., 2021), grid-based methods are

also used to model uncertainty where epistemic and

aleatoric uncertainties are distinguished, leading

to the assignment of long-term goals to individual

grid cells. Other models, such as HOME (Gilles

et al., 2021) and THOMAS (Gilles et al., 2022b),

utilize grid maps for efﬁcient trajectory sampling.

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

101

Unimodal Trajectories Multimodal Trajectories Multimodal Parametric

Distributions

Multimodal Non-

parametric Distributions

Figure 2: Overview of various unimodal and multimodal output representations. The two images on the left represent

trajectory-based methods, while the two on the right depict parametric and non-parametric occupancy approaches.

To enhance safety while still primarily predicting

detected objects in the whole scene, Luo et al. (Luo

et al., 2021) introduce a method to explicitly consider

undetected instances through a graph representation.

Moving to a scene-centric perspective, Toyungy-

ernsub et al. (Toyungyernsub et al., 2022) predict

occupancies from raw point clouds without requiring

object classiﬁcations. To separate dynamic from

static objects, a semantic segmentation process is

employed, followed by the prediction of moving

objects using the Dempster–Shafer Theory (DST).

Mahjourian et al. (Mahjourian et al., 2022) extend

this representation by proposing occupancy ﬂow

ﬁelds to predict directional movements, enabling

collision-free path predictions for multiple agents.

While non-parametric methods provide a potential

framework for instance- and tracking-free develop-

ments, they are limited by the inherent inaccuracy of

discretized representations.

Parametric Prediction. Gaussian Mixture Mod-

els (GMMs) represent a parametric variant to occu-

pancy prediction methods, where spatial probabilities

are represented using Gaussian components, each de-

ﬁned by their mean and standard deviation in a con-

tinuous 2D space (McLachlan and Basford, 1988).

These models capture spatial complexity within a

scene with fewer components and in a less sparse for-

mat, providing computational efﬁciency and high ac-

curacy compared to non-parametric approaches. As

such, they are often used as intermediate representa-

tions during the trajectory generation as seen in meth-

ods like Trajectron++ (Salzmann et al., 2020), Proph-

Net (Wang et al., 2023), and MTR++ (Shi et al.,

2024). In these approaches, Gaussian components are

estimated for each agent before sampling diverse tra-

jectories to produce multimodal outputs. While para-

metric models effectively integrate spatial uncertainty

(Wiest et al., 2012), their application to represent oc-

cupancies in an object-invariant, scene-centric man-

ner has yet to be explored.

3 METHODOLOGY

This section outlines our experiments, starting with

the problem formulation and the dataset preprocess-

ing. We then introduce our input features, the oc-

cupancy representation, and the model architecture.

Lastly, we explain the training procedure and evalu-

ation process, ensuring comparability with trajectory

prediction methods.

3.1 Problem Formulation

The problem of probabilistic pedestrian prediction is

deﬁned as follows: Given a 2D map of the trafﬁc

environment and sets of observed positions X

1:T

, p

, . . . , p

} for B agents (i ∈ B) over time horizon

T , for each future timestep t predict the most likely

positions

1:D

= {p

, p

, . . . , p

} for A predictable

pedestrians represented by D probability distributions

where A ⊆ B. The idea is to combine pedestrians who

are in close proximity, modeling them with a single

distribution and avoiding unnecessarily detailed pre-

dictions. Each position at timestep t is parameterized

by Cartesian coordinates p

= {x

, y

} ∈ R

For predictable pedestrians, the observed time

horizon T contain ten entries sampled at 10 Hz re-

sulting in a motion history of one second. In accor-

dance with the Argoverse 2 motion forecasting chal-

lenge, predictions are generated for six seconds into

the future. While the available sampling frequency

equals 10 Hz, the ground-truth positions Y

1:A

T +1:T +T

, p

T +1:T +T

, . . . , p

T +1:T +T

} are sampled

at the lower frequency of 1 Hz. This choice was made

given the lower velocities of pedestrians compared

to other trafﬁc participants, balancing computational

load and accuracy, and to improve generalization by

preventing overﬁtting on the noisy data annotations.

As a result, the prediction horizon T

is deﬁned by six

timesteps.

Simplifying the notation, X and Y represent the

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

102

observed and ground-truth trajectories, respectively,

and

Y denotes the predicted future probability distri-

butions. The loss aims to minimize the distance be-

tween predicted distributions

Y and ground-truth tra-

jectories Y for all predictable pedestrians.

3.2 Preprocessing and Input Features

We use a pedestrian benchmark (Uhlemann et al.,

2025) based on the Argoverse 2 Motion Forecasting

Dataset (Wilson et al., 2021) as it provides a diverse

and rich collection of pedestrian trajectories in urban

trafﬁc environments. Since the provided data is in an

agent-centric format, the ﬁrst step contained center-

ing the coordinate frame around the ego vehicle to

allow for the prediction of shared distributions. To

focus on relevant agents only, predictions are limited

to pedestrians within a 50 m radius of the ego vehi-

cle (Zhou et al., 2022). This range ensures a balance

between prediction accuracy and computational efﬁ-

ciency, as it captures over 80 % of pedestrians. The

information for each agent is stored in a social ma-

trix of shape 33 × 21, where the ﬁrst dimension cor-

responds to the maximum number of pedestrians ob-

served within that radius. The second dimension en-

codes the features for each agent i shown in Equation

1. Here, the agent type (pedestrian, vehicle, motorcy-

clist, cyclist, or bus) and the historical trajectory are

considered. To align with previous methods, the ob-

servation length is limited to ten timesteps, as this du-

ration is considered sufﬁcient for the prediction task

(Ettinger et al., 2021).

[type

, x

, y

, x

T −1

, y

T −1

, . . . , x

T −9

, y

T −9

] (1)

The arrangement of the social matrix entries is de-

termined by sorting agents by type and their distance

from the ego vehicle (Uhlemann et al., 2025). This

ensures that predictable pedestrians are prioritized

for inclusion in the prediction process, followed by

other agents they may interact with. While this rep-

resentation relies on precise tracking, an alternative,

tracking-free method was implemented. In this ap-

proach, only three features [type

, x

, y

] are recorded

for each agent i at each timestep t, resulting in a ma-

trix of dimensions 10 × 33 × 3. Afterward, the ob-

served agents are sorted by distance from the ego at

each timestep, eliminating explicit object association.

To evaluate this method’s effectiveness and assess the

model’s reliance on tracking overall, a comparison

with a random sorting approach is conducted as well.

The map is represented using semantic polygons,

each deﬁned by several edge vectors. Semantic types

include drivable areas, lane segments, and pedestrian

crossings. To consider this information, a map ma-

trix of dimensions 730× 6 is constructed, focusing on

Figure 3: Example for a vectorized map as contained in the

Argoverse 2 dataset, depicting a grey polygon for the driv-

able area A and red ones for pedestrian crossings B, C, and

D. Corresponding edges for each polygon are depicted with

small letters. On the right side, the generated map feature

matrix used as input for our model is shown.

edges within a 70 m radius of the ego vehicle. This

radius builds on the 50 m radius of the social matrix,

with an extra 20 m to provide predictable pedestrians

with additional context. On average, 730 edges fall

within this range, determining the matrix’s ﬁrst di-

mension. If more edges are present, only the 730 clos-

est are retained, sorted by distance to the ego vehicle.

The second dimension corresponds to the features of

each vector, which include the semantic type, the el-

ement id, and scene-centric x- and y-coordinates for

each edge’s start- and endpoints. Figure 3 illustrates

this representation alongside an exemplary map, with

a grey polygon for drivable area A and red ones for

crosswalks B, C, and D.

3.3 Occupancy Generation

As one of the main contributions of this work, we

introduce a concept for continuous, probabilistic oc-

cupancy prediction focused on both individuals and

object groups. Instead of learning distributions from

scratch, ground-truth clusters are generated as a ba-

sis for the training. Among various clustering meth-

ods (Rupali Nehete, 2016), the Density-Based Spatial

Clustering of Applications with Noise (DBSCAN)

algorithm (Ester et al., 1996) was selected for its

ability to identify clusters without prior knowledge

of their number. It requires only two parameters:

min samples, deﬁning the minimum points for a clus-

ter, and eps, describing the maximum distance be-

tween two points in the same cluster. Inspired by

GMMs, each cluster is represented as a Gaussian dis-

tribution, with the mean and standard deviation de-

ﬁned by its center and maximum spread. This is in

contrast to previous methods, where each individual

has a separate GMM assigned (Wiest et al., 2012;

Salzmann et al., 2020). Overall, this approach inte-

grates both, spatial uncertainty and enhanced robust-

ness against noisy training data into the predicted out-

put (Karle et al., 2022; Guo et al., 2019).

Ground-truth distributions are generated using

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

103

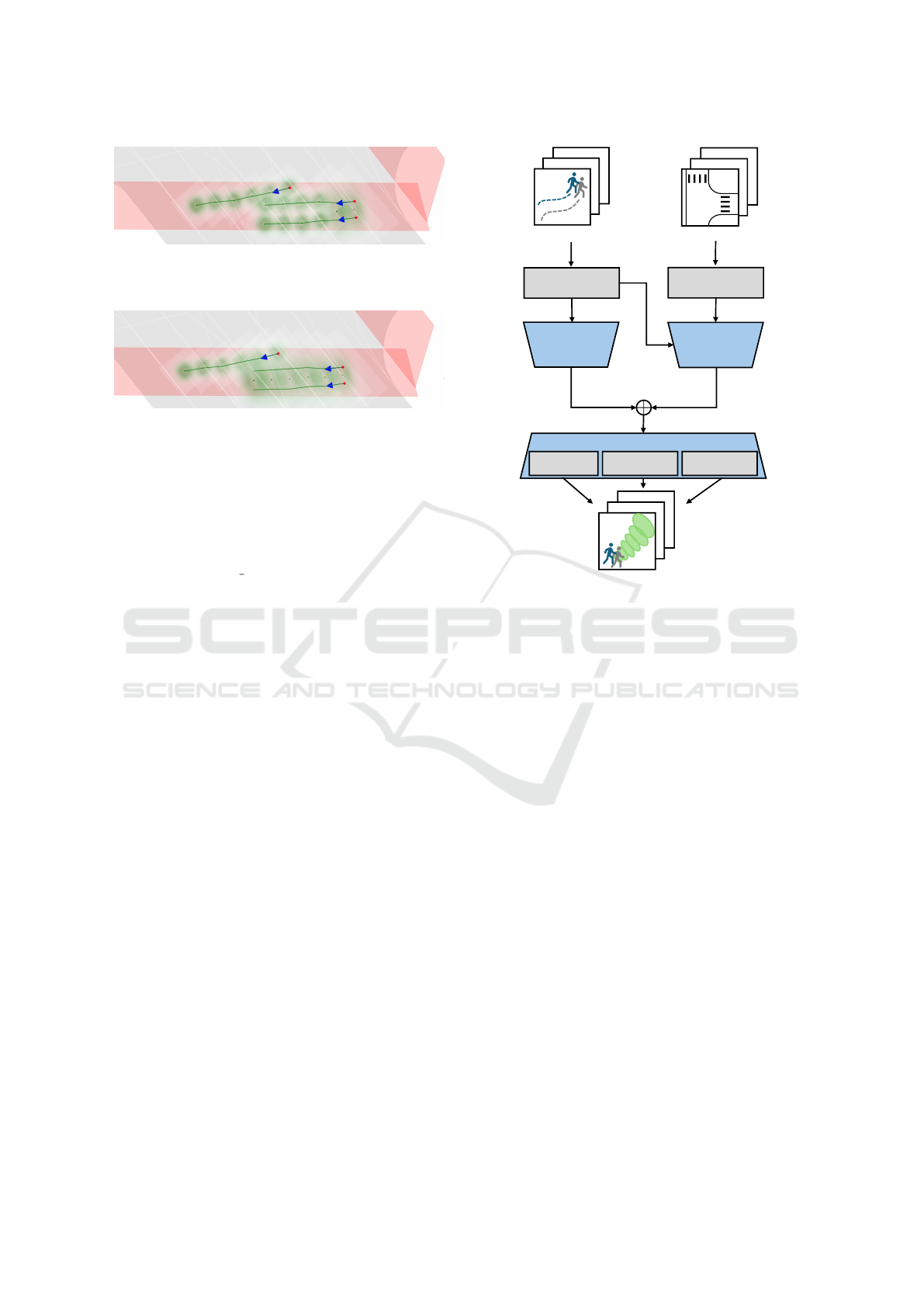
(a) Results for DBSCAN with eps = 1.5. The pedestrian

group only forms a cluster for the ﬁrst two timesteps al-

though belonging together for the whole duration.

(b) Results for DBSCAN with eps = 2.0. The pedestrian

group is clustered together for all timesteps while still keep-

ing the individual to the left separate.

Figure 4: Comparison of outcomes for the DBSCAN clus-

tering algorithm with two different distance thresholds. The

scenarios depict three pedestrians visualized by red dots

crossing the road over a crosswalk.

DBSCAN with min

samples = 1 and eps = 2.0 de-

ﬁned as Euclidean distance, ensuring agents within a

2 m radius are grouped while preserving sparsely pop-

ulated clusters. The 2 m radius was determined em-

pirically through observations, balancing meaningful

cluster formation while preserving distinct intentions

of individuals as shown in Figure 4. Here, three

pedestrians visualized with red dots cross the street

along a crosswalk, with two pedestrians belonging to

a group. While setting eps = 1.5 results only in partial

clusters being formed, eps = 2.0 combines the two

humans to a single distribution across all timesteps.

The last step involves determining the mean and

covariance of each cluster, such that a Gaussian distri-

bution can be formed. The location can be calculated

as the average of all positions within the cluster, while

the standard deviation can be obtained by the maxi-

mum distance (max) in the x- and y-directions from

the cluster center. Additionally, a margin of 0.5 m is

added to this value to incorporate a safety margin as

well as to account for the dimensions of human bod-

ies.

3.4 Model Architecture

To implement the model architecture, we follow pre-

vious approaches (Lan et al., 2024; Wang et al., 2023;

Salzmann et al., 2020), where two separate encoders

for social and semantic information are employed,

facilitating parallel encoding as shown in Figure 5.

The social encoder extracts the agent features and in-

Embedding

[N, 33, 128]

[N, 730, 128]

Query

[N, 2, 18, 18]

Concatenate

Predictions

[N, 33, 21]

Map Tensor

Social

Encoder

Map

Encoder

Embedding

Social Tensor

[N, 730, 6]

[N, 2, 18, 18]

[N, 4, 18, 18]

Probability

Decoder

Mean Scale

Figure 5: Overview of the proposed model architecture.

teractions from the social matrix (Yuan et al., 2021;

Zhou et al., 2023), while the map encoder extracts

spatial and semantic information from the map ma-

trix and models the agent-map interactions. The de-

coder receives the concatenated output of both en-

coders and predicts the agents’ future distributions for

the next six seconds using a fully-connected architec-

ture. Both encoders are inspired by Snapshot (Uhle-

mann et al., 2025), while the decoder is inspired by

HiVT (Zhou et al., 2022).

The social encoder is depicted in Figure 6 and em-

beds the input tensor via a fully-connected layer with

layer normalization, expanding the feature dimension

to 128. Multi-head self-attention is applied through a

single transformer layer with eight heads, incorporat-

ing skip connections, layer normalization, and linear

layers (Vaswani et al., 2017). After post-processing

to further embed relevant features, the dimension is

reduced to N × 2 × 18 × 18. The map encoder shares

the same architecture, with the only difference being

the use of a cross-attention module to both extract

semantic information and model agent-map dynam-

ics. Social embeddings act as queries, while map em-

beddings serve as keys and values (Uhlemann et al.,

2025; Zhou et al., 2023). For the tracking-free ver-

sion, both encoders require slight modiﬁcations due

to the differently shaped input tensor. Here, the input

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

104

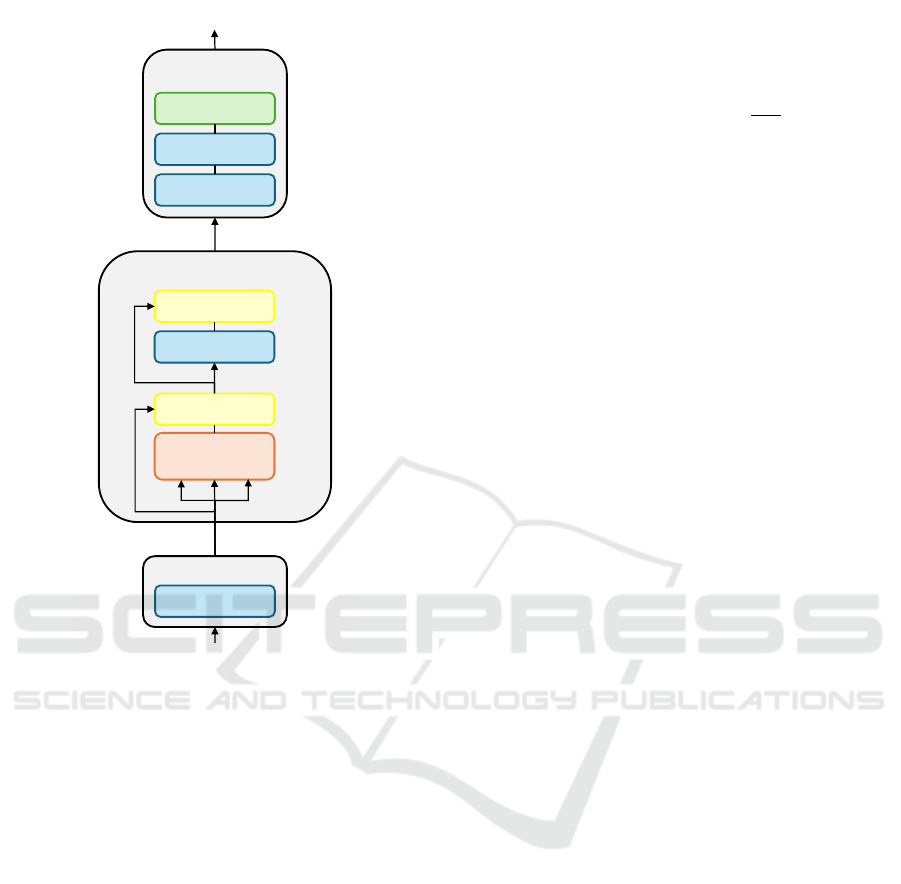
Feature

Encoding

Transformer Layer

x L

Input Embedding

Social Tensor

[N, 33, 21]

Linear + Norm

Multi-Head

Attention

Linear + Norm

Conv + Norm

Add + Norm

Linear

Add + Norm

[N, 33, 128]

[N, 2, 18, 18]

Figure 6: Detailed architecture of the social encoder block.

tensor has the dimensions N × 10 × 33 × 3, which is

reshaped to N × 330 × 3 to align with the proposed

layout. Similarly, the output of the map encoder is

adapted to handle the N × 330 × 128 embedding for-

mat. After concatenating both encoder outputs along

the channel dimension, producing a tensor of shape

N × 4 × 18 × 18, the latent features are passed to the

decoder.

The decoder reﬁnes the latent representation

through an initial upsampling and encoding step

where a transposed convolution layer followed by

two convolutional layers in conjunction with batch

normalization are used. Afterward, two linear lay-

ers with layer normalization are employed for fea-

ture sharing before being fed into three separate feed-

forward stages to generate the existence probability,

mean, and scale parameter of each Gaussian distribu-

tion (Wang et al., 2023; Shi et al., 2024; Lin et al.,

2024). In contrast to traditional mixture models, we

allow the likelihood of each distribution to be within

[0, 1] to model individual occupancies, which is ac-

complished by using a sigmoid function. The output

dimensions of our model are N × D for distribution

probabilities, N × D × T

× 2 for their 2D positions,

and N × D × T

× 4 for the covariance matrix, ensur-

ing positive deﬁniteness. The covariance matrix Σ is

parameterized as



r σ



with ρ =

and r describ-

ing the covariance between x and y. With this setup,

our model has 585445 parameters in total.

3.5 Training Procedure

Using the generated ground-truth clusters as detailed

in Section 3.3, a direct comparison between clusters

and predicted distributions as seen in Figure 7 be-

comes possible. Here, three ground-truth positions

(red crosses) are represented by two ground-truth

clusters as depicted by the green ellipses around their

mean locations. Further, two predicted distributions

are visualized in blue and purple with corresponding

mean positions and covariances. While a direct com-

parison between ground-truth clusters and predicted

distributions is possible, the order of the predictions

should not inﬂuence the outcome.

To guarantee permutation invariance, we were in-

spired by object detection frameworks like DETR

(Carion et al., 2020) which use the Hungarian Al-

gorithm to match predicted and ground-truth bound-

ing boxes. Adopting this approach, a cost matrix is

created by calculating the pairwise distance between

each ground-truth cluster and the predicted ones. To

handle padded values and non-valid predictions with

probabilities below 0.5, we assign a value of 1 × 10

to these entries, encouraging associations between

non-valid elements. For the example in Figure 7, this

method would lead to a 2×2 cost matrix. After the as-

sociation is made through the Hungarian Algorithm,

the loss is computed by comparing ground-truth and

predicted distributions across three parameters: loca-

tions, covariances, and probabilities. Although we

initially considered the Kullback-Leibler divergence

for efﬁciency, its sensitivity to disjoint distributions

led us to separate the optimization of location and co-

variance. This results in a loss function with three

individual terms weighted by λ:

Loss = λ

loc

+ λ

cov

+ λ

(2)

The location loss L

loc

is computed as the Eu-

clidean distance for valid ground-truth clusters, while

the covariance loss L

cov

is optimized using the L2

norm over the variance and correlation dimensions

in x- and y-direction. Subsequently, these two terms

are averaged across all timesteps t and distributions

D. For the optimization of the probability loss L

we compute the L1 distance between the ground-truth

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

105

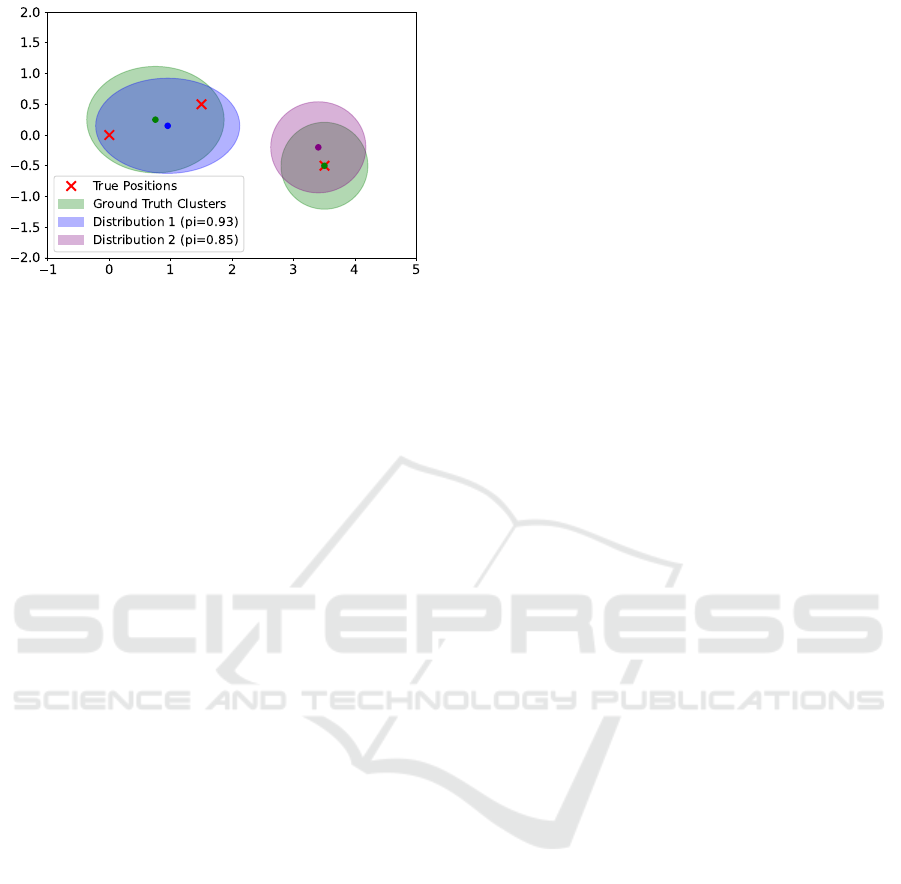
Figure 7: Exemplary ground-truth clusters and predicted

distributions. In this example, the left ground-truth cluster

should be associated to distribution 1, while the right should

be matched with distribution 2.

mask and predicted probabilities, guiding valid pre-

dictions toward one and padding toward zero. Rather

than calculating the average, we sum values across

distributions such that incorrect predictions have a

higher impact. For the example in Figure 7, the prob-

ability loss is given by L

= (1−0.93)+(1−0.85) =

0.22.

To train the network, we choose a batch size of

128, balancing generalization and memory efﬁciency.

Starting with a learning rate of 6 × 10

−3

, the rate de-

cays if the validation loss shows no improvement over

ﬁve epochs. For the optimizer, we select AdamW

(Loshchilov and Hutter, 2019). Our framework is

developed in PyTorch (Paszke et al., 2019) utiliz-

ing a single NVIDIA Tesla V100 GPU with 16 GB

RAM. With this setup, the training terminated after

100 epochs on average.

3.6 Metrics and Evaluation

To evaluate the model’s performance, we use the Av-

erage Displacement Error (ADE) and Final Displace-

ment Error (FDE). The ADE measures the average

Euclidean distance between ground truth and predic-

tions across the prediction horizon, while FDE only

considers the ﬁnal predicted position. For multimodal

predictors, we select the most likely of six predicted

trajectories to better represent a real-world applica-

tion rather than the Best-of-K approach as commonly

adopted. Additionally, we use the Miss Rate (MR)

to determine the quantity of predictions closely fol-

lowing the ground truth. Following the Argoverse 2

(Wilson et al., 2021) convention, we evaluate the MR

for the ﬁnal timestep and deﬁne a miss if the pre-

diction is farther than two meters from the ground

truth. This aligns with group behavior dynamics as

agents can be clustered into one distribution within a

two-meter radius. Nevertheless, an implementation of

the MR averaged over all timesteps is also provided,

giving insight into the error accumulation over time.

To compare our framework with traditional methods

and observed ground-truth trajectories, we employ a

sampling-based approach drawing 50 random sam-

ples from each distribution at every timestep. After-

ward, for each ground-truth position we compute the

minimum and maximum distances to the nearest pre-

dicted distribution. This way, a broader measure of

distribution accuracy can be achieved since potential

false negatives are accounted for. Finally, using these

two distances, we calculate the four previously intro-

duced metrics for each scene, providing a more com-

prehensive comparison to trajectory-based prediction

methods.

4 RESULTS

After having presented our methodology, we now

compare our model to state-of-the-art prediction ap-

proaches given the metrics presented in Section

3.6. Alongside, we present the performance of the

tracking-free implementations and analyze two sce-

narios in a qualitative manner.

4.1 Quantitative Comparison

We evaluate our approach by comparing it to the

Constant Velocity (CV) baseline and the state-of-the-

art motion prediction models SIMPL (Zhang et al.,

2024), QCNet (Zhou et al., 2023), and Snapshot (Uh-

lemann et al., 2025). For better comparability, Snap-

shot is evaluated both at 10 Hz and 1 Hz. As previ-

ously mentioned, we report the accuracy of our model

based on the closest (min) and farthest (max) of 50

generated samples. Table 1 summarizes the results on

the test set of the Argoverse 2 pedestrian benchmark,

including the three model variations outlined in Sec-

tion 3.2: Randomly sorted social inputs (No Tracking

& Sorting), inputs sorted by distance without explicit

object association (No Tracking), and inputs incorpo-

rating tracked object histories.

Focusing on the tracking-based model, being

shown in the last two rows of the chart, a spread

of approximately 0.8 m is observed between the min

and max ADE and FDE values, a range consis-

tent across all model variations. While this behav-

ior is discussed further in Section 5, we use the

minimal values as a proxy for the overall accuracy

when compared to trajectory-based methods. In terms

of ADE, our model scores last with an average er-

ror of 0.877 m, falling behind the CV baseline with

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

106

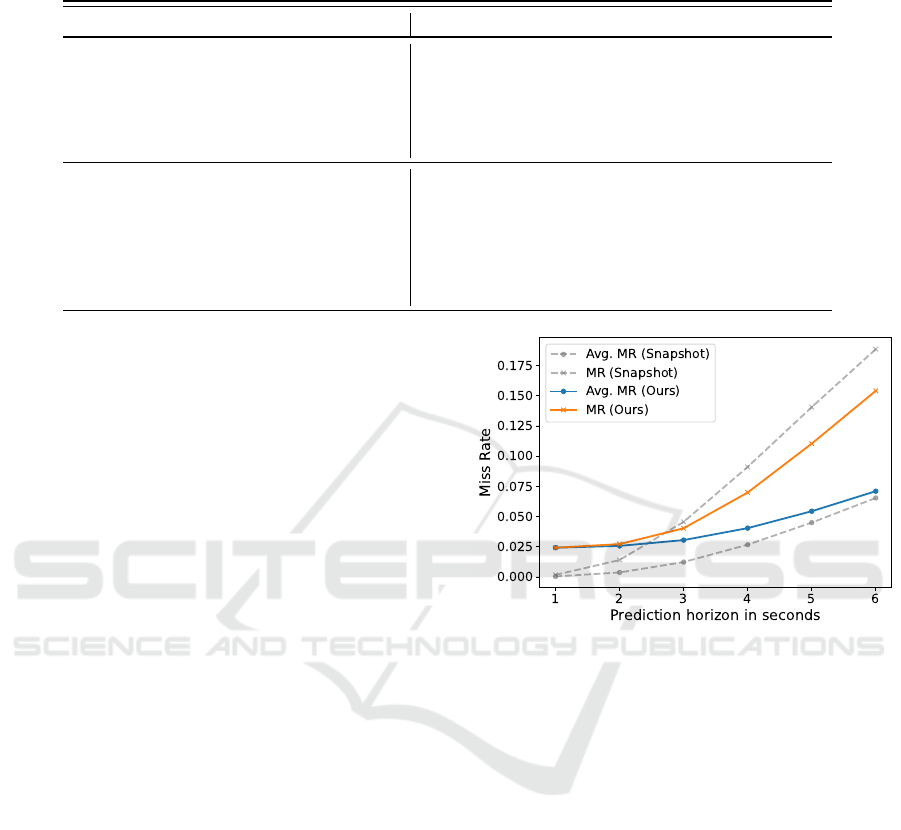
Table 1: Performance of different models as well as variations of our approach on the Argoverse 2 pedestrian benchmark. All

models in the top section of the chart are evaluated at 10 Hz unless stated otherwise.

Model ADE in m ↓ FDE in m ↓ Avg. MR ↓ MR ↓

CV 0.793 1.776 0.096 0.279

SIMPL (Zhang et al., 2024) 0.699 1.557 - 0.243

QCNet (Zhou et al., 2023) 0.693 1.474 - 0.217

Snapshot (1 Hz) (Uhlemann et al., 2025) 0.664 1.255 0.080 0.189

Snapshot (Uhlemann et al., 2025) 0.567 1.255 0.065 0.189

Ours (max) - No Tracking - No Sorting 2.316 2.938 0.376 0.521

Ours (min) - No Tracking - No Sorting 1.529 2.058 0.220 0.329

Ours (max) - No Tracking 1.731 2.291 0.215 0.371

Ours (min) - No Tracking 0.977 1.412 0.099 0.193

Ours (max) 1.651 2.129 0.194 0.337

Ours (min) 0.877 1.248 0.071 0.154

(0.793 m). The best results are achieved by Snap-

shot with 0.567 m, while the other models consis-

tently score below 0.7 m. However, when Snapshot

is evaluated at 1 Hz, the gap to our model narrows to

0.21 m, suggesting that its accuracy partly arises from

noise modeling at higher sampling rates. For the FDE,

the results differ: Here, our approach matches Snap-

shot with a slight advantage. This difference is fur-

ther highlighted in the MR metric, where our model

achieves the best performance by a signiﬁcant mar-

gin, indicating its ability to capture overall dynamics

despite limitations in replicating precise trajectories.

Lastly, although Snapshot achieves the highest aver-

age MR at 10 Hz, our model excels again when it is

evaluated at the same sampling frequency of 1 Hz.

Examining the model variants shown in the last

six rows of Table 1, the model incorporating tracked

object histories achieves the best results. The No

Tracking variant, which sorts agents by distance, per-

forms comparably well, with a difference in ADE of

just 0.1 m and 0.164 m for the FDE, outperforming

QCNet. When considering the MR, while still lack-

ing behind the ﬁrst version of our model, it achieves

a similar performance to Snapshot. In contrast, the

No Tracking & Sorting variation, using randomly dis-

tributed agents in the input tensor, performs signiﬁ-

cantly worse for all metrics, with ADE and FDE val-

ues of 1.529 m and 2.058 m, respectively. Scoring

consistently lower than the CV baseline, it suggests

that the model struggles to predict accurate pedestrian

locations and actions, performing similar to the max-

imum values of the tracking-based version.

To better compare the performance of our occu-

pancy representation with trajectory prediction meth-

ods, we analyze the accuracy with respect to the MR

and the averaged MR for different prediction hori-

zons, as shown in Figure 8. Here, the accuracy

of our method is plotted with colored graphs, while

Figure 8: Prediction accuracy reported by the MR and the

average MR over the next 6 s for our method and Snapshot.

Snapshot’s scores are plotted in grey as a reference.

For predictions one second into the future, Snap-

shot achieves a near-perfect score for both metrics,

while our method shows a MR of 2.4 %. However,

at six seconds ahead, our model demonstrates a sim-

ilar average MR and outperforms Snapshot with re-

spect to the MR. Analyzing the overall trend of the

graphs, both models exhibit a constant incline over

time. However, Snapshot’s incline is steeper and be-

gins approximately one second earlier, resulting in a

higher MR starting from three seconds onward. For

the average MR, which aggregates results across all

previous timesteps, Snapshot beneﬁts from its previ-

ously low values. Nonetheless, the results for the MR

indicate that the predicted occupancies can more ef-

fectively capture the future motion dynamics within

the observed scenes.

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

107

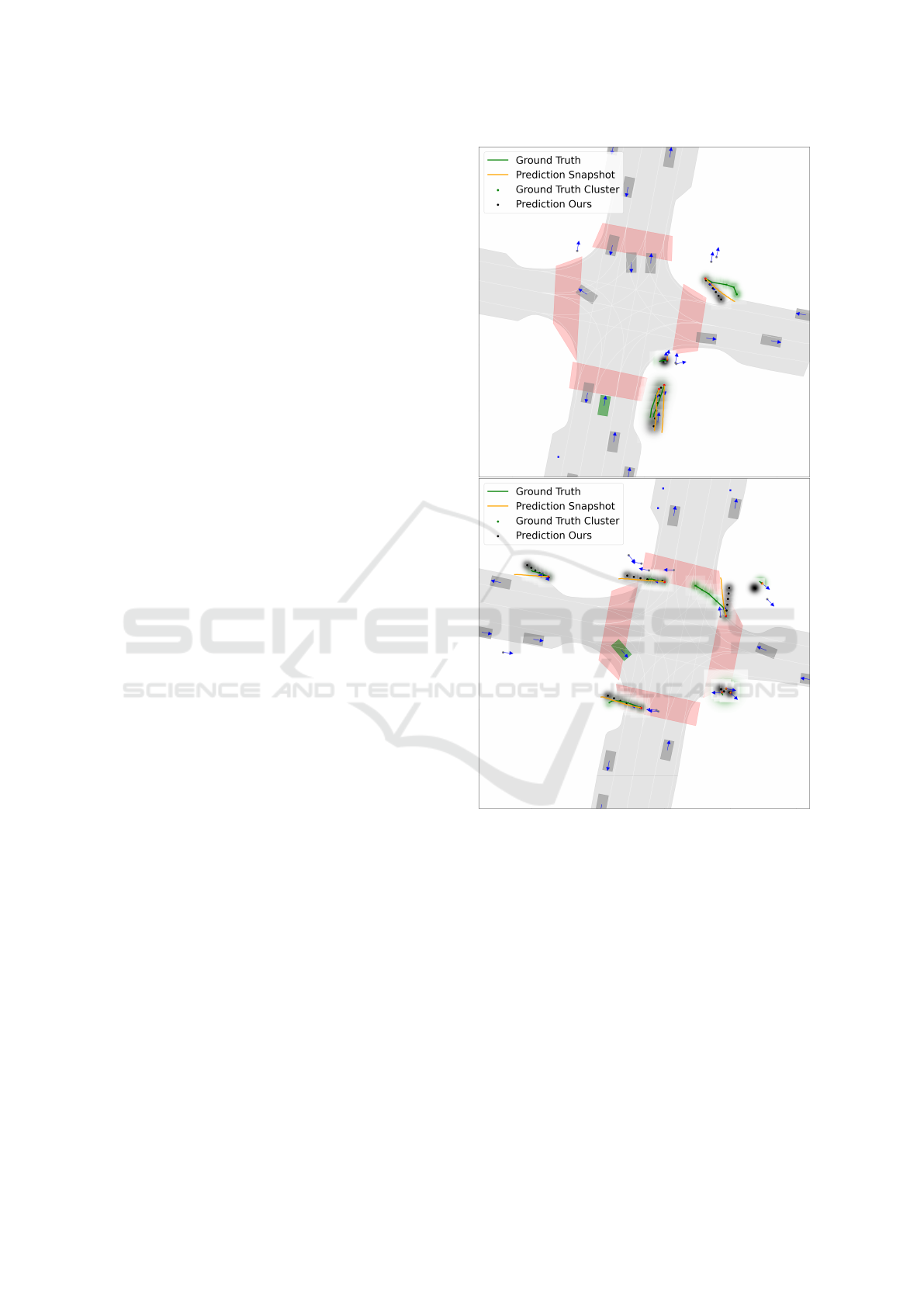
4.2 Qualitative Comparison

In this section, representative scenarios are examined

to gain deeper insights into the models’ behaviors and

to explore potential causes for the performance differ-

ences observed. Figure 9 illustrates two scenarios in-

volving pedestrians at intersections, featuring static,

linear, and non-linear motion patterns. In the ﬁrst

scenario depicted on top, four pedestrians can and

are being predicted. The static pedestrian near the

right crosswalk is correctly anticipated as such, while

the group of pedestrians walking downward is repre-

sented by a shared linear distribution, accurately cap-

turing their group behavior. Although the prediction

slightly overestimates their speed, it successfully re-

ﬂects their intention and is more accurate than Snap-

shot. However, the pedestrian at the top, exhibiting

starkly non-linear movement, is not accurately cap-

tured by either model, highlighting a general chal-

lenge in predicting such actions solely based on the

observed motion history.

In the second scenario, eight predictable pedestri-

ans are contained, which all are more or less repre-

sented by a distribution. Starting with the dynamic

pedestrians along the crosswalks, the top and bottom

ones’ directions are accurate but the speed is slightly

too fast. The pedestrian on the right, cutting cor-

ners to cross the top crosswalk, is more challeng-

ing to predict. Both models handle the initial two

timesteps well but fail to anticipate the directional

change. For the pedestrian in the top left, while the

predicted speed is still slightly too fast, our model

captures the action again more accurately than Snap-

shot. At the bottom right, three pedestrians, which

could have been combined into a single distribution

based on the ground truth, are instead predicted by

three individual distributions. Although not ideal,

this still reﬂects their intentions and does not pose

safety risks. However, the static pedestrian at the top

right, though correctly identiﬁed, is represented with

a distribution slightly shifted from its actual position.

While such shifts could be safety-critical near the ego

vehicle, we observe them only for more distant pre-

dictions, likely due to the scene-centric representation

used. In summary, our model performs well in most

cases, particularly for linear and static motion, though

predictions are sometimes slightly too fast or not op-

timally combined. For non-linear cases, where even

trajectory prediction models struggle, our approach

also encounters challenges, indicating inherent difﬁ-

culties in anticipating complex motion patterns based

on the provided data.

Figure 9: Two scenarios from the Argoverse 2 dataset, de-

picting predicted pedestrians visualized by red dots around

intersections. In both cases, the ground-truth distributions

and ground-truth trajectories are highlighted in green, while

the predicted distributions are marked in black. As refer-

ence, agent headings are indicated by blue arrows and pre-

dicted trajectories from Snapshot are shown in orange.

5 DISCUSSION

Based on the previous ﬁndings, this section discusses

our methodology and results in three key aspects: (1)

the evaluation of our occupancy representation com-

pared to traditional trajectory prediction methods, (2)

the applicability of our approach based on its accuracy

and runtime, and (3) the strengths and weaknesses of

employing a tracking-free approach, along with po-

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

108

tential areas for improvement.

5.1 Evaluation Procedure

As shown in Table 1, we use a min-max strategy

to quantify the variability in values predicted by our

occupancy method for a single individual. Across

all model variations, a moderate spread of approx-

imately 0.8 m for ADE and FDE can be observed,

which is consistent with our expectations. For single-

agent scenarios, even with perfect predictions, a de-

fault spread of 0.4 m arises from the safety margin

introduced during ground-truth generation in Section

3.3. For the multi-agent case, considering the com-

bined distribution of two pedestrians with a maximum

standard deviation of 1.5 m for eps = 2.0, a spread of

around 1.12 m is expected. Hence, the difference of

0.8 m indicates the tendency to predict bigger, shared

clusters, aligning with the intended outcome of our

approach. While the maximum distance quantiﬁes

the distributions’ spread with respect to a single in-

dividual, it provides limited information about overall

accuracy, as some variability is inherent when com-

bining individuals into a shared distribution. There-

fore, a more suitable evaluation would quantify the

minimum and maximum values considering all agents

captured by a given Gaussian. As a result, focusing

on the minimal values for the comparison conducted

in this study offers a sufﬁcient measure of accuracy.

Additionally, the ﬁxed sample size of 50 provides

a built-in regularization, as smaller distributions are

more likely to yield smaller min values, while larger

distributions reduce this likelihood.

5.2 Model Performance

The qualitative analysis of the scenarios in Figure 9

shows that more straightforward linear or static cases

are generally well captured, albeit not always per-

fectly combined. However, more dynamic scenarios

present challenges, as our method, as well as compa-

rable trajectory prediction methods, struggle to antic-

ipate complex motion patterns based on the provided

data. These ﬁndings align with the quantitative re-

sults in Section 4.1, showing that while trajectory pre-

diction models exhibit low ADE values due to their

detailed output representation, our approach captures

the overall scene dynamics equally well, offering a

comparable or better FDE and MR. Therefore, incor-

porating additional contextual cues or raw sensor data

might be necessary as neither model architecture nor

output representation seems to make a difference. Re-

gardless, as our model is technically still an unimodal

predictor, the uncertainty-based occupancy modeling

seems to enhance the safety for vulnerable road users,

as the MR is notably improved for prediction horizons

beyond 2 s shown in Figure 8. For a practical applica-

tion though, it needs to be guaranteed that each pedes-

trian is covered at least by one predicted distribution

as highlighted in Figure 9.

Besides accuracy, the inference speed of our ap-

proach is important to allow for real-time predic-

tions. Here, we measured an average inference time

of 8.97 ms on a NVIDIA Tesla V100 GPU to pre-

dict the whole scene. Thanks to the scene-centric

representation, this value remains constant regardless

of the number of agents, as predictions are gener-

ated in parallel. While the presented method accom-

modates 33 agents only, this framework can easily

be extended due to the ﬂexible input structure em-

ployed. Although the current performance already

meets the requirements of real-time systems operat-

ing at 10 Hz, further optimizations, such as an im-

proved preprocessing or a low-level implementation

promise further enhancements. Moreover, the abil-

ity to predict shared distributions contributes to the

scalability of our method. While the groups in Fig-

ures 9 (top) and 11 are successfully combined, reduc-

ing computational load, the three static individuals in

Figure 9 (bottom) provide an exception. We noticed

that these typically occur for agent groups either far-

ther from the ego vehicle, or containing more than

two entities. The former is likely due to less accurate

observations at greater distances, while the latter re-

ﬂects the rarity of larger groups in the dataset. Hence,

to address these limitations, alternative datasets with

more diverse scenarios need to be explored. Despite

these challenges, the results demonstrate the viability

of this approach as a foundation for future work.

5.3 Tracking-Free Approach

The results in Table 1 indicate that both tracking-free

implementations cannot match the version utilizing

tracked inputs, but we think that the underlying rea-

sons differ. The random-ordering variant performs the

worst, which is expected: Although transformer ar-

chitectures are permutation-invariant (Vaswani et al.,

2017), the input order matters during the embedding

generation performed by the fully connected layer

employed. While this might be partially compen-

sated for in the training process, architectural changes

would be required to handle these inputs effectively.

Therefore, sorting by distance offers a practical com-

promise by enforcing a deterministic input order,

scoring only slightly below the tracked implemen-

tation and requiring little computational overhead.

While this could be seen as a form of tracking as of-

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

109

ten the distance between individuals and the AV re-

mains consistent for several observations, that is not

the case as no explicit object associations are made

across timesteps. Remarkably, although this variant

does not match the tracked version’s MR, its perfor-

mance remains comparable to, or better than, all tra-

jectory prediction methods evaluated. Therefore, it

offers a promising and practically viable option for

future developments.

The reasons for this performance can be found in

Figure 11, comparing the prediction outcomes of the

three variations side by side. Starting with the bottom

one showcasing the tracked version, the predicted dis-

tributions almost perfectly match ground-truth ones.

This becomes a bit worse when only sorting is used

as shown in the center image. Although the individ-

ual is still accurately predicted, the group dynamics

are slightly off while still being correctly summarized.

On the contrary, the model using randomly ordered

agents does not recognize the group at all, only pre-

dicting the two pedestrians in the top. While we al-

ready covered the cause for this behavior above, we

observe that the sorting variant seems to have difﬁcul-

ties associating cluster centers and motion for groups

larger than two. This is likely due to the limited

samples available for such groups and the continu-

ous scene-centric representation, making it difﬁcult

for the model to generalize for these cases. With suf-

ﬁcient data, this performance gap could potentially

be closed. Besides, future improvements might in-

clude tailored training strategies, architectural modiﬁ-

cations to enhance the feature sharing during the em-

bedding, or alternative scene representations. Here,

object locations could serve as anchors for distribu-

tions, simplifying the cluster assignment.

6 CONCLUSIONS

This work introduces a promising framework for

tracking-free, shared probabilistic occupancy predic-

tion. While not the most accurate in terms of ADE,

our method outperforms trajectory-based approaches

in FDE and MR, effectively capturing scene dynam-

ics and unpredictable behaviors to enhance safety.

Due to its scene-centric design and the prediction of

shared group distributions, an average inference time

of 8.97 ms per scene is achieved. While the absence

of tracked motion results in a slight performance

drop, a competitive MR compared to other models is

achieved, highlighting its potential. Future improve-

ments could focus on incorporating contextual data

(e.g., trafﬁc light states, raw point clouds) and reﬁn-

ing the input representation for improved handling of

Figure 10: Comparison of all three model variations for

a single scenario, being random sorting, distance-based

sorting, and tracking implementation from top to bottom.

Here, ground-truth distributions and trajectories are shown

in green, whereas predicted distributions are highlighted in

black. As a reference, Snapshot’s predictions are marked in

orange.

tracking-free features.

ACKNOWLEDGMENTS

As the ﬁrst author, Nico Uhlemann initiated the idea

of this paper and contributed essentially to its concep-

tion, implementation, and content creation. Melina

ordehoff made vital contributions during the de-

sign, implementation and analysis of the proposed

approach. Markus Lienkamp shaped the research

project and critically revised the outlined work. As a

guarantor, he accepts responsibility for the overall in-

tegrity of the paper. This research was funded by the

Central Innovation Program (ZIM) under grant No.

KK5213703GR1.

REFERENCES

Becker, S., Hug, R., H

ubner, W., and Arens, M. (2019).

Red: A simple but effective baseline predictor for

the trajnet benchmark. In Computer Vision – ECCV

2018 Workshops, pages 138–153. Springer Interna-

tional Publishing.

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

110

Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kir-

illov, A., and Zagoruyko, S. (2020). End-to-end ob-

ject detection with transformers. In Computer Vi-

sion – 16th European Conference, Proceedings Part I,

volume 12346, pages 213–229. Springer International

Publishing and Imprint Springer.

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In KDD’96: Pro-

ceedings of the Second International Conference on

Knowledge Discovery and Data Mining, pages 226–

231. AAAI Press.

Ettinger, S., Cheng, S., Caine, B., Liu, C., Zhao, H., Prad-

han, S., Chai, Y., Sapp, B., Qi, C., Zhou, Y., Yang, Z.,

Chouard, A., Sun, P., Ngiam, J., Vasudevan, V., Mc-

Cauley, A., Shlens, J., and Anguelov, D. (2021). Large

scale interactive motion forecasting for autonomous

driving : The waymo open motion dataset. In 2021

IEEE/CVF International Conference on Computer Vi-

sion, Proceedings, pages 9690–9699. IEEE.

Gilles, T., Sabatini, S., Tsishkou, D., Stanciulescu, B.,

and Moutarde, F. (2021). Home: Heatmap output

for future motion estimation. In 2021 IEEE Interna-

tional Intelligent Transportation Systems Conference

(ITSC), pages 500–507. IEEE.

Gilles, T., Sabatini, S., Tsishkou, D., Stanciulescu, B.,

and Moutarde, F. (2022a). Gohome: Graph-oriented

heatmap output for future motion estimation. In 2022

IEEE International Conference on Robotics and Au-

tomation (ICRA), pages 9107–9114. IEEE.

Gilles, T., Sabatini, S., Tsishkou, D., Stanciulescu, B., and

Moutarde, F. (2022b). THOMAS: Trajectory heatmap

output with learned multi-agent sampling. In Interna-

tional Conference on Learning Representations.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2020). Generative adversarial networks. Com-

mun. ACM, 63:139–144.

Gulzar, M., Muhammad, Y., and Muhammad, N. (2021). A

survey on motion prediction of pedestrians and vehi-

cles for autonomous driving. IEEE Access, 9:137957–

137969.

Guo, Y., Kalidindi, V. V., Arief, M., Wang, W., Zhu, J.,

Peng, H., and Zhao, D. (2019). Modeling multi-

vehicle interaction scenarios using gaussian random

ﬁeld. In 2019 IEEE Intelligent Transportation Sys-

tems Conference, pages 3974–3980. IEEE.

Gupta, A., Johnson, J., Fei-Fei, L., Savarese, S., and

Alahi, A. (2018). Social gan: Socially acceptable

trajectories with generative adversarial networks. In

2018 IEEE/CVF Conference on Computer Vision and

Pattern Recognition, Proceedings, pages 2255–2264.

IEEE.

Huang, R., Zhuo, G., Xiong, L., Lu, S., and Tian, W. (2023).

A review of deep learning-based vehicle motion pre-

diction for autonomous driving. Sustainability, page

14716.

Huang, Y., Du, J., Yang, Z., Zhou, Z., Zhang, L., and Chen,

H. (2022). A survey on trajectory-prediction methods

for autonomous driving. IEEE Transactions on Intel-

ligent Vehicles, 7(3):652–674.

Hussain, R. and Zeadally, S. (2019). Autonomous cars: Re-

search results, issues, and future challenges. IEEE

Communications Surveys & Tutorials, 21(2):1275–

1313.

Jain, A., Casas, S., Liao, R., Xiong, Y., Feng, S., Segal,

S., and Urtasun, R. (2019). Discrete residual ﬂow for

probabilistic pedestrian behavior prediction. In Con-

ference on Robot Learning.

Karle, P., Geisslinger, M., Betz, J., and Lienkamp, M.

(2022). Scenario understanding and motion predic-

tion for autonomous vehicles—review and compari-

son. IEEE Transactions on Intelligent Transportation

Systems, 23(10):16962–16982.

Kosaraju, V., Sadeghian, A., Mart

ın-Mart

ın, R., Reid,

I., Rezatoﬁghi, S. H., and Savarese, S. (2019).

Social-BiGAT: multimodal trajectory forecasting us-

ing bicycle-GAN and graph attention networks. Cur-

ran Associates Inc.

Lan, Z., Jiang, Y., Mu, Y., Chen, C., and Li, S. E. (2024).

SEPT: Towards efﬁcient scene representation learning

for motion prediction. In The Twelfth International

Conference on Learning Representations.

Lange, B., Itkina, M., and Kochenderfer, M. J. (2021). At-

tention augmented convlstm for environment predic-

tion. 2021 IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS), pages 1346–

1353.

Lefevre, S., Vasquez, D., and Laugier, C. (2014). A survey

on motion prediction and risk assessment for intelli-

gent vehicles. Robomech Journal, 1.

Lin, L., Lin, X., Lin, T., Huang, L., Xiong, R., and

Wang, Y. (2024). Eda: Evolving and distinct an-

chors for multimodal motion prediction. Proceed-

ings of the AAAI Conference on Artiﬁcial Intelligence,

38(4):3432–3440.

Loshchilov, I. and Hutter, F. (2019). Decoupled weight

decay regularization. In International Conference on

Learning Representations.

Luo, K., Casas, S., Liao, R., Yan, X., Xiong, Y., Zeng, W.,

and Urtasun, R. (2021). Safety-oriented pedestrian oc-

cupancy forecasting. In 2021 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 1015–1022.

Mahjourian, R., Kim, J., Chai, Y., Tan, M., Sapp, B.,

and Anguelov, D. (2022). Occupancy ﬂow ﬁelds

for motion forecasting in autonomous driving. IEEE

Robotics and Automation Letters, 7(2):5639–5646.

Mangalam, K., An, Y., Girase, H., and Malik, J. (2021).

From goals, waypoints & paths to long term human

trajectory forecasting. In 2021 IEEE/CVF Interna-

tional Conference on Computer Vision, Proceedings,

pages 15213–15222. IEEE.

McLachlan, G. J. and Basford, K. E. (1988). Mixture

models: Inference and applications to clustering, vol-

ume 84. Dekker.

Mohamed, A., Zhu, D., Vu, W., Elhoseiny, M., and Claudel,

C. (2022). Social-implicit: Rethinking trajectory pre-

diction evaluation and the effectiveness of implicit

maximum likelihood estimation. In Computer Vision

Exploring Shared Gaussian Occupancies for Tracking-Free, Scene-Centric Pedestrian Motion Prediction in Autonomous Driving

111

– 17th European Conference, Proceedings, Part XXII,

page 463–479. Springer-Verlag.

Ngiam, J., Caine, B., Vasudevan, V., Zhang, Z., Chiang, H.-

T. L., Ling, J., Roelofs, R., Bewley, A., Liu, C., Venu-

gopal, A., Weiss, D., Sapp, B., Chen, Z., and Shlens, J.

(2022). Scene transformer: A uniﬁed architecture for

predicting multiple agent trajectories. In The Tenth In-

ternational Conference on Learning Representations.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

Pytorch: An imperative style, high-performance deep

learning library. In Advances in Neural Information

Processing Systems, volume 32. Curran Associates,

Inc.

Ridel, D., Deo, N., Wolf, D., and Trivedi, M. (2020).

Scene compliant trajectory forecast with agent-centric

spatio-temporal grids. IEEE Robotics and Automation

Letters, 5(2):2816–2823.

Ridel, D. A., Rehder, E., Lauer, M., Stiller, C., and Wolf,

D. F. (2018). A literature review on the prediction of

pedestrian behavior in urban scenarios. 21st Interna-

tional Conference on Intelligent Transportation Sys-

tems (ITSC), pages 3105–3112.

Rudenko, A., Palmieri, L., Doellinger, J., Lilienthal, A.,

and Arras, K. (2021). Learning occupancy priors of

human motion from semantic maps of urban environ-

ments. IEEE Robotics and Automation Letters, pages

1–1.

Rupali Nehete, Y. G. (2016). A survey on trajectory cluster-

ing models. National Conference on Advancements in

Computer & Information Technology, (1):20–24.

Salzmann, T., Ivanovic, B., Chakravarty, P., and Pavone,

M. (2020). Trajectron++: Dynamically-feasible tra-

jectory forecasting with heterogeneous data. In Com-

puter Vision – 16th European Conference, Proceed-

ings, volume 12363, pages 683–700. Springer Inter-

national Publishing.

Schuetz, E. and Flohr, F. B. (2024). A review of trajec-

tory prediction methods for the vulnerable road user.

Robotics, 13(1):1.

Shi, S., Jiang, L., Dai, D., and Schiele, B. (2024). Mtr++:

Multi-agent motion prediction with symmetric scene

modeling and guided intention querying. IEEE trans-

actions on pattern analysis and machine intelligence,

46(5):3955–3971.

Sohn, K., Yan, X., and Lee, H. (2015). Learning structured

output representation using deep conditional gener-

ative models. In Proceedings of the 28th Interna-

tional Conference on Neural Information Processing

Systems, page 3483–3491. MIT Press.

Toyungyernsub, M., Yel, E., Li, J., and Kochenderfer, M. J.

(2022). Dynamics-aware spatiotemporal occupancy

prediction in urban environments. In 2022 IEEE/RSJ

International Conference on Intelligent Robots and

Systems (IROS), pages 10836–10841.

Uhlemann, N., Fent, F., and Lienkamp, M. (2024). Eval-

uating pedestrian trajectory prediction methods with

respect to autonomous driving. IEEE Transactions

on Intelligent Transportation Systems, 25(10):13937–

13946.

Uhlemann, N., Zhou, Y., Mohr, T., and Lienkamp, M.

(2025). Snapshot: Towards application-centered mod-

els for pedestrian trajectory prediction in urban trafﬁc

environments. In Proceedings of the IEEE/CVF Win-

ter Conference on Applications of Computer Vision

Workshops. IEEE.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L., and Polosukhin, I.

(2017). Attention is all you need. In 31st Conference

on Neural Information Processing Systems.

Wang, X., Su, T., Da, F., and Yang, X. (2023). Proph-

net: Efﬁcient agent-centric motion forecasting with

anchor-informed proposals. In 2023 IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

Proceedings, pages 21995–22003. IEEE.

Wiest, J., Hoffken, M., Kresel, U., and Dietmayer, K.

(2012). Probabilistic trajectory prediction with gaus-

sian mixture models. In 2012 IEEE Intelligent Vehi-

cles Symposium (IV 2012), pages 141–146. IEEE.

Wilson, B., Qi, W., Agarwal, T., Lambert, J., Singh, J.,

Khandelwal, S., Pan, B., Kumar, R., Hartnett, A.,

Pontes, J. K., Ramanan, D., Carr, P., and Hays, J.

(2021). Argoverse 2: Next generation datasets for

self-driving perception and forecasting. In Proceed-

ings of the Neural Information Processing Systems

Track on Datasets and Benchmarks.

Yao, Y., Atkins, E., Johnson-Roberson, M., Vasudevan, R.,

and Du, X. (2021). Bitrap: Bi-directional pedes-

trian trajectory prediction with multi-modal goal es-

timation. IEEE Robotics and Automation Letters,

6(2):1463–1470.

Yuan, Y., Weng, X., Ou, Y., and Kitani, K. (2021). Agent-

former: Agent-aware transformers for socio-temporal

multi-agent forecasting. In 2021 IEEE/CVF Interna-

tional Conference on Computer Vision: ICCV 2021,

Proceedings, pages 9793–9803. IEEE.

Zamboni, S., Kefato, Z. T., Girdzijauskas, S., Nor

en, C.,

and Dal Col, L. (2022). Pedestrian trajectory pre-

diction with convolutional neural networks. Pattern

Recognition, 121:108252.

Zhang, L., Li, P., Liu, S., and Shen, S. (2024). Simpl:

A simple and efﬁcient multi-agent motion prediction

baseline for autonomous driving. IEEE Robotics and

Automation Letters, 9(4):3767–3774.

Zhao, H. and Wildes, R. P. (2021). Where are you heading?

dynamic trajectory prediction with expert goal exam-

ples. In 2021 IEEE/CVF International Conference on

Computer Vision (ICCV), pages 7609–7618.

Zhou, Z., Wang, J., Li, Y.-H., and Huang, Y.-K.

(2023). Query-centric trajectory prediction. In 2023

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition Proceedings, pages 17863–17873.

IEEE.

Zhou, Z., Ye, L., Wang, J., Wu, K., and Lu, K. (2022).

Hivt: Hierarchical vector transformer for multi-agent

motion prediction. In 2022 IEEE/CVF Conference on

Computer Vision and Pattern Recognition, Proceed-

ings, pages 8813–8823. IEEE.

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

112