Pattern Recognition in Biosequences Using Artificial Immune System
Luiz Paulo Liberato
a
,
´
Alvaro Magri Nogueira da Cruz
b
, Anderson Rici Amorim
c
,
Vitoria Zanon Gomes
d
, Bruno Rodrigues da Silveira
e
, Gabriel Augusto Prevato
f
,
Luiza Guimar
˜
aes Cavarc¸an
g
, Carlos Roberto Val
ˆ
encio
h
and Geraldo Francisco Doneg
´
a Zafalon
∗ i
Department of Computer Science and Statistics, Universidade Estadual Paulista (UNESP), Rua Crist
´
ov
˜
ao Colombo, 2265,
Jardim Nazareth, S
˜
ao Jos
´
e do Rio Preto - SP, 15054-000, Brazil
{luiz.liberato, alvaro.magri, anderson.amorim, vitoria.zanon, bruno.rodrigues-silveira, gabriel.prevato, luiza.cavarcan,
Keywords:
Bioinformatics, Artificial Immune System, Pattern Recognition.
Abstract:
With the advance on genomic studies was possible to know better the genetic inheritance, protein synthesis
and mutations that occurs in living beings. With the increase in the DNA sequencing capacity, and its storage,
advanced biological studies are possible. To ensure timely and greater precision in the pattern recognition
process, heuristic methods are used, since deterministic methods make it impossible to execute large volumes
of data. Heuristic methods have the characteristic of seeking the best possible solution within the search
space that is explored. Among the known heuristics is the Artificial Immune System (AIS), which falls under
the category of bioinspired methods that simulate biological behavior. In this work, the CLONALG (Clonal
Selection Algorithm) of the AIS approach was implemented with HMM (Hidden Markov Model) as an affinity
function, in order to obtain stochastic patterns with biological relevance and an acceptable computational
time. As a result, a 50% more relevant value was obtained in terms of execution time, when compared to
CLONALG with the Hamming affinity function. Finally, it was also validated that CLONALG with the HMM
implementation was able to recognize the same patterns when compared to similar tools.
1 INTRODUCTION
Finding patterns in biosequences is a challenging
task. Over the years, numerous researchers have made
efforts to make this goal achievable, both from a com-
putational point of view and from a biological point
of view (Kucherov, 2019). The chosen strategy must
combine both aspects, as this way it is possible to ob-
tain a pattern with biological generation at an accept-
able computational cost.
The search for patterns in DNA, RNA and pro-
teins consumes computational resources, and in some
cases the execution time makes it impossible to find
a
https://orcid.org/0009-0003-0145-8195
b
https://orcid.org/0000-0002-7918-0109
c
https://orcid.org/0000-0001-7862-7530
d
https://orcid.org/0000-0003-4176-566X
e
https://orcid.org/0009-0003-5941-9869
f
https://orcid.org/0009-0001-7091-9763
g
https://orcid.org/0009-0007-9589-3217
h
https://orcid.org/0000-0002-9325-3159
i
https://orcid.org/0000-0003-2384-011X
∗
Corresponding author
the optimal solution (da Cruz et al., 2023). To mit-
igate such problems, several heuristics were created
and extended, but for certain situations, combinations
of several strategies are necessary, to execute the task
in an acceptable time and obtain an optimal value or
close to the optimal value. Thus, the solution pro-
posed in this work fits this need.
The hybridization of methods has been widely ex-
plored in the context of bioinformatics, therefore, this
work presents an algorithm that combines two meth-
ods, the CLONALG (Clonal Selection Algorithm)
from the AIS (Artificial Immune System) class of al-
gorithms and HMM (Hidden Markov Models). The
combination of both offers variability and biological
quality, it is hoped that such an approach will con-
tribute to the pattern recognition context and serve as
an inspiration for several other combinations of ap-
proaches.
In this work, the CLONALG (Clonal Selection
Algorithm) of the AIS approach was implemented
with HMM (Hidden Markov Model) as an affinity
function, in order to obtain stochastic patterns with
biological relevance and an acceptable computational
time.
Liberato, L. P., Nogueira da Cruz, Á. M., Amorim, A. R., Gomes, V. Z., Rodrigues da Silveira, B., Prevato, G. A., Cavarçan, L. G., Valêncio, C. R. and Zafalon, G. F. D.
Pattern Recognition in Biosequences Using Artificial Immune System.
DOI: 10.5220/0013293500003929
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 797-804
ISBN: 978-989-758-749-8; ISSN: 2184-4992
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
797

This work is organized as follows: In Section 2,
we present the related works, In Section 3 we detail
our methodology to develop the approach. In Section
4, we show the results of our method, focusing on
time execution improvement. Finally, in Section 5,
we make our conclusions about the work.
2 RELATED WORK
This section presents works that used the CLONALG
(Clonal Selection Algorithm) in several types of prob-
lems, which presented satisfactory results. It is also
shown a pattern recognition algorithm that served as
the basis for tests and validations. Thus, it is possible
to observe important characteristics from a computa-
tional point of view that will be discussed later in this
work.
The optimization of multimodal functions is a
challenging task that basically consists of finding the
global optima, several studies in the field of compu-
tation inspired by nature have been widely applied in
this context. CLONALG is applied to the solution
of problems of this nature as cited by Dasgupta et al.
(2011).
Luo et al. (2019) uses the niching method (Horn
et al., 1994) to divide the population into subpopula-
tions, which seek to converge to a global optimum. As
subpopulations converge a small population is gener-
ated. A differential evolution (DE) mutation operator
is incorporated into the algorithm to accelerate con-
vergence, which leads to higher performance.
Implemented by Yavuz et al. (2018), a tertiary
protein structure prediction method, the protein sec-
ondary structure dictionary (DSSP) was used as a
guide. DSSP represents different secondary structures
represented by H, G, I, E, B, T, S, and C. To reduce
the complexity of the prediction the structures were
reduced by transforming {H, G} into {H}, {E, B} in
{E} and the rest in {C}.
The task of predicting the tertiary structure of pro-
teins is complex and extremely necessary, as the con-
formation of the protein from the interaction between
amino acids determines its biological function (Dill
et al., 1995). There are several studies referring to
this context, which use the primary structure to infer
the tertiary structure.
The clonal selection algorithm (CLONALG) was
used by Fefelova et al. (2020), with two mutation
strategies to increase population variability, differen-
tial evolution algorithm (DE) and differential evolu-
tion mutation operator trigonometric (TDE), in order
to escape from great places. A hybrid algorithm for
Figure 1: Schematic representation of the Pyramid-Based
Common Subsequence Search Algorithm (PCSS).
the prediction of the tertiary structure was then
developed.
According to the HP Dill model (Hirst, 1999),
amino acids are divided into two types: hydrophilic
and hydrophobic, water-soluble and insoluble, re-
spectively (Aftabuddin and Kundu, 2007). Hy-
drophilic ones are denoted by P and hydrophobic ones
by H. The amino acid sequence can be represented by
S = (s
1
, s
2
, s
3
,..., s
n
), s
i
∈ {H, P}, i = 1, n.
According to D’Angelo and Palmieri (2020) on
December 31, 2019, in Wuhan (Hubei province,
China) an outbreak of pneumonia cases of unknown
etiology was identified. On January 9, 2020, the
Chinese Centers for Disease Control and Prevention
(CDC) recognized a new SARS-CoV-2 coronavirus.
On March 11, 2020, the World Health Organization
(WHO) declared COVID-19 as the disease caused by
SARS-CoV-2, and a warning to the world of a global
pandemic.
It is proposed by D’Angelo and Palmieri (2020)
to create two algorithms for pattern recognition. The
former is responsible for discovering common subse-
quences called PCSS (pyramidal-based common sub-
sequences search), while the latter SCPS (Sliding
columns-based pattern search) is used to find multi-
ple combinations of these substrings.
The idea of the PCSS algorithm is based on
the join and pruning process, which is responsible
for joining common consecutive substrings to form
longer substrings and pruning substrings that are not
consecutive. The subsequences are created in the
form of a pyramid as shown in the Figure 1.
The SCPS algorithm is dedicated to discovering
repetitive patterns of common substrings. For that,
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
798

Figure 2: Matrix M
l
for l = 1 , 2 , 3.
Figure 3: Pattern search algorithm based on sliding columns
(SCPS).
a column alignment process of the matrix M
l
(Fig-
ure 2) is used. More precisely, for a given level l
a given common substring of the reference genome,
the columns of the remaining genomes are shifted to
be aligned with the considered substring, as shown in
Figure 3.
3 THE PROPOSED METHOD
This section will describe in detail which techniques,
sets of sequences and distance measurements the al-
gorithm uses, in order to elucidate its operation and
contributions to the pattern recognition process.
3.1 CLONALG-HMM
The CLONALG algorithm is based on the AIS ap-
proach that fits into the set of bioinspired evolutionary
algorithms. The Hidden Markov Model (HMM) was
chosen as a distance measure, instead of the standard
distance measures, Hamming distance and Euclidean
distance, for example. The justification for adopt-
ing such an approach is its stochastic characteristic,
Figure 4: Flowchart of the CLONALG-HMM algorithm.
which offers a satisfactory solution in an acceptable
execution time and a result with biological relevance.
Tests were performed with the Hamming distance,
the results obtained from a computational point of
view were not very satisfactory, as deterministic ap-
proaches for a large amount of sequences makes
the process infeasible, considering that the algorithm
needs some iterations to improve the quality of the
pattern. Thus, the HMM was implemented, as it is a
widely used approach in the context of pattern recog-
nition as described by Sun and Buhler (2007).
To assess the affinity of the (subsequences) with
the antigens that are the input sequences, the algo-
rithm uses a probability that a subsequence occurs in
the set of input sequences. With this measure of affin-
ity it is possible to apply a mutation inversely propor-
tional to the affinity, that is, the greater the affinity
of the antibody with the antigens (input sequences),
the lower the mutation rate, and a rate for generating
clones directly proportional to the affinity of the anti-
body, as described by De Castro (2006).
User-supplied parameters for the algorithm are:
• S: biosequence set;
• max_it: number of iterations to run;
• n1: number of iterations to run;
• n2: percentage of antibodies with low affinity.
The figure 4 shows the main flow of the algorithm.
The algorithm receives a set of sequences that are
used for training the HMM, then subsequences are
generated, which are the possible patterns ranging
Pattern Recognition in Biosequences Using Artificial Immune System
799

from 3 to 9 nucleotides, as used by D’Angelo and
Palmieri (2020). Each nucleotide will be generated
randomly, in order to form a subsequence, which will
be evaluated through the probability of belonging to
the set of input sequences. The subsequences with the
highest probability are selected for the next iteration,
according to the maximum affinity parameter n1 and
substrings with low affinity are discarded according
to the minimum affinity parameter n2, both informed
by the user.
The processing flow is described below, with the
steps of how the CLONALG algorithm works with
the HMM.
• Step 1: DNA sequences are provided to the algo-
rithm for pattern extraction;
• Step 2: a Markov Model is created to represent
these sequences, to be described in the subsection
3.2;
• Step 3: antibodies (subsequences) of sizes be-
tween 3 and 9 are generated randomly nu-
cleotides;
• Step 4: the affinities of the antibodies with the
antigens (input sequences) are evaluated;
• Step 5: the most likely antibodies are selected,
based on the parameter n1 informed by the user;
• Step 6: antibodies with higher affinity are cloned
at a rate directly proportional to their affinity;
• Step 7: clones are mutated at a rate inversely pro-
portional to their affinity;
• Step 8: the clones’ affinities in relation to the anti-
gens are evaluated;
• Step 9: the clones with the highest affinities are
selected, according to the parameter n1;
• Step 10: memory cells are created, which store
the antibodies, during the execution of the algo-
rithm these memory cells can be replaced by oth-
ers with greater affinity;
• Step 11: antibodies with the lowest affinities are
replaced by others, according to the parameter n2
informed by the user, new antibodies are gener-
ated at random;
• Step 12: the antibodies (subsequences) generated
at the end of the iterations are passed as a param-
eter to the method that generates the patterns.
At the end of the execution of the algorithm, the
patterns of the input sequences are extracted. To val-
idate these patterns, comparisons were made with the
patterns found by D’Angelo and Palmieri (2020) and
will be shown in the 4 section.
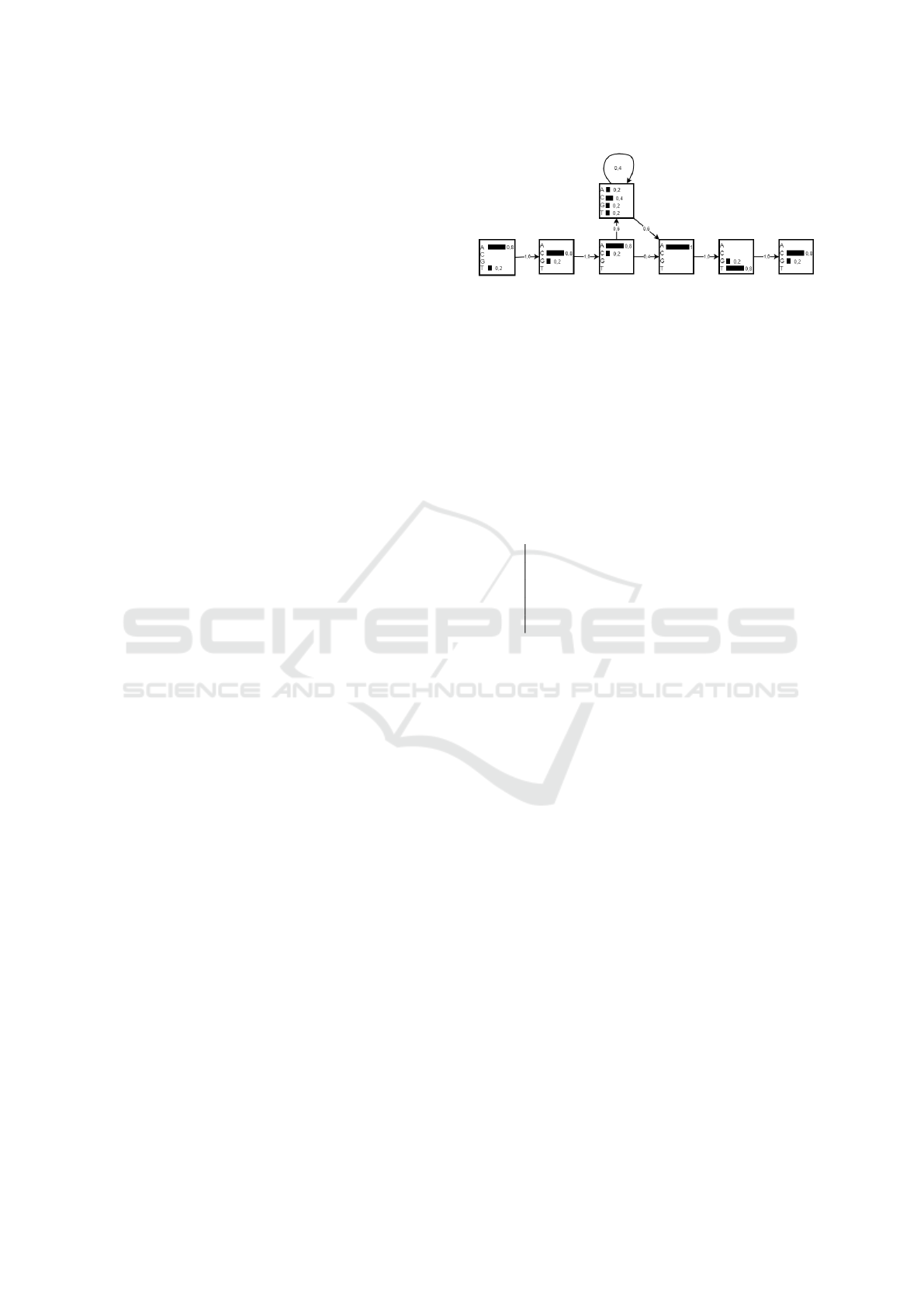
Figure 5: Hidden Markov Model.
3.2 Hidden Markov Model as a
Measure of Affinity
The Hidden Markov Model is built from input se-
quences, called antigens, in the abstraction of the
CLONALG algorithm. The template is created based
on counting all alphabetic characters (A, C, T, G) of
the sequences in position i, where i is the index of
the column in row j. Assume the following DNA se-
quences:
Table 1: Examples of DNA Sequences.
1 A C A - - - A T G
2 T C A A C T A T C
3 A C A C - - A G C
4 A G A - - - A T C
5 A C C G - - A T C
From the sequences in Table 1, a score is gener-
ated with 4/5=0.8 for an A in the first position and
1/5=0.2 for a T because it is observed that of the 5
letters, 4 are As and 1 is T. Similarly in the second
position the probability of C is 4/5 and of G 1/5, and
so on. After the third position in the alignment, 3 of
the 5 sequences have ‘inserts’ of different lengths, so
the probability of having a insertion is 3/5 and, con-
sequently, 2/5 of not having (which correspond to the
sequences that have 3 holes in positions 3, 4 and 5).
The Figure 5 shows these odds.
Assuming that you want to evaluate the score of
the ACCATC sequence, you have the following Equa-
tion 1:
P(ACACATC) = 0.8 ∗ 1 ∗ 0.8 ∗ 1 ∗ 0.8 ∗ 0.6
∗0.4 ∗ 0.6 ∗ 1 ∗ 1 ∗ 0.8 ∗ 1 ∗ 0.8 ≈ 4.7 ∗ 10
−2
(1)
In this way, it is possible to evaluate the score of
the subsequences generated by the CLONALG algo-
rithm, and thus use the subsequence selection mecha-
nism with greater affinity with the MMO. This allows
you to generate a population at random, and in the
course of iterations the affinity increase. The section
4 shows which data were used in the tests and which
results were obtained.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
800

4 RESULTS AND DISCUSSION
The aim of the tests is to find patterns in the region of
the SARS-CoV-2 genomes responsible for synthesiz-
ing the Spike protein, which according to D’Angelo
and Palmieri (2020) is located at position 21300 to
25400. used in the tests were downloaded from the
Genbank
1
database, 100 sequences were used and se-
lected in the period from 01/01/2020 to 03/06/2020
(filter ”Release Date”) and ordered by the (”Length”
column) in descending order. With these sequences,
it was possible to compare the patterns obtained with
the patterns found by D’Angelo and Palmieri (2020).
All tests were run in C# .NET Core 2.2 envi-
ronment on a 64-bit Windows 10 PC, with Intel(R)
Core(TM) i7-8565U CPU @ 1.80GHz with 8.00GB
of RAM. The project is available on GitHub
2
for con-
sultation and possible updates.
First, it is necessary to prove that the algorithm is
able to extract patterns, for that it was executed with
n1 = 0.6, which means that 60% of the antibodies with
high affinity will be selected for the next generation,
n2 = 0.4 which means 40% of the antibodies with
low affinity will be replaced by others generated ran-
domly, and finally the parameter max it = 100, which
is the number of iterations of the algorithm. The table
2 displays the found patterns.
Table 2: Patterns found for n1 = 0.6; n2 = 0.4 and max it
= 100.
Patterns
CLONALG-HMM D’ANGELO; PALMIERI
1 TTT TTT
2 GAT GAT
3 TCT TCT
4 ATA ATA
5 ATG ATG
6 CAA CAA
7 ACT ACT
8 TGG TGG
9 TAAA TAAA
10 CGCT CGCT
11 - ATTTTG
With the results displayed in Table 2, it is possi-
ble to prove that the algorithm is indeed capable of
finding patterns. But only with its execution, it is not
suitable to have a broader view of the behavior of the
data, since it is an evolutionary algorithm that can of-
fer approximate solutions. For this reason, there are
some tables that have data referring to 10 executions
for each iteration (max it), with average number of
1
https://www.ncbi.nlm.nih.gov/genbank/
sars-cov-2-seqs/\#reference-genome
2
https://github.com/lpliberato/CLONALG-HMM
standards, average time and standard deviations.
By analyzing the Tables 3 to 18, one can have a
broader view about the behavior of the data. Note
that the average number of patterns found varies be-
tween 8 and 9, and the result obtained by D’Angelo
and Palmieri (2020) was 11. It is natural that the av-
erage of patterns found is less than 11 because it is
a probabilistic model, which does not mean that in
some execution of the algorithm the 11 patterns were
not found. The CLONALG-HMM algorithm uses as a
measure of affinity the Hidden Markov Model, which
is a stochastic approach, to evaluate its efficiency,
several comparisons were made with the measure of
Hamming’s affinity, which is a deterministic measure,
and it was proved that CLONALG-HMM offers bet-
ter results (more patterns and less execution time) as
shown in the tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17 e 18.
Table 3: Number of patterns n1 = 0.6 e n2 = 0.4.
CLONALG-HMM
max it Patterns (average) Standard deviation
10 9 1.33333
50 9 0.94281
100 ≈ 9 0.73786
500 ≈ 9 0.63246
1000 ≈ 9 0.82327
5000 ≈ 9 0.97183
Table 4: Runtime (in seconds) n1 = 0.6 e n2 = 0.4.
CLONALG-HMM
max it Time (s) Standard deviation
10 0.11678 0.06630
50 0.10760 0.02421
100 0.09012 0.02051
500 0.11686 0.06416
1000 0.11008 0.02843
5000 0.14025 0.04547
Table 5: Number of patterns n1 = 0.6 e n2 = 0.4.
CLONALG-HAMMING
max it Patterns (average) Standard deviation
10 ≈ 8 1.42984
50 ≈ 8 0.91894
100 ≈ 8 0.94868
500 ≈ 9 0.87560
1000 ≈ 9 0.67495
5000 9 0.00000
The intention is to offer an evolutionary approach
to the pattern recognition solution, to collaborate with
the future works cited by D’Angelo and Palmieri
(2020). Therefore, this work can contribute to the ad-
vancement of research on this topic, and also receive
Pattern Recognition in Biosequences Using Artificial Immune System
801

Table 6: Runtime (in seconds) n1 = 0.6 e n2 = 0.4.
CLONALG-HAMMING
max it Time (s) Standard Deviation
10 0.24764 0.06673
50 0.25940 0.03678
100 0.23959 0.02531
500 0.25510 0.04029
1000 0.23930 0.06151
5000 0.30113 0.03530
Table 7: Number of patterns n1 = 0.7 e n2 = 0.3
CLONALG-HMM
max it Patterns (average) Standard Deviation
10 ≈ 9 1.03280
50 ≈ 9 0.82327
100 9 0.66667
500 ≈ 9 0.78881
1000 ≈ 9 0.78881
5000 ≈ 9 0.91894
Table 8: Runtime (in seconds) n1 = 0.7 e n2 = 0.3
CLONALG-HMM
max it Time (s) Standard Deviation
10 0.10391 0.08034
50 0.09341 0.01493
100 0.10182 0.01858
500 0.10060 0.02985
1000 0.11550 0.01852
5000 0.13532 0.02013
Table 9: Number of patterns n1 = 0.7 e n2 = 0.3.
CLONALG-HAMMING
max it Patterns (average) Standard deviation
10 ≈ 9 0.82327
50 ≈ 9 0.84984
100 ≈ 8 1.13529
500 ≈ 9 0.84327
1000 ≈ 8 0.96609
5000 ≈ 8 1.28668
Table 10: Runtime (in seconds) n1 = 0.7 e n2 = 0.3.
CLONALG-HAMMING
max it Time (s) Standard Deviation
10 0.28211 0.16348
50 0.26065 0.05568
100 0.23601 0.04286
500 0.25395 0.05403
1000 0.26503 0.02161
5000 0.31255 0.09295
Table 11: Number of patterns n1 = 0.8 e n2 = 0.2.
CLONALG-HMM
max it Patterns (average) Standard Deviation
10 ≈ 8 1.71270
50 ≈ 9 0.73786
100 ≈ 9 0.70711
500 ≈ 9 1.17851
1000 ≈ 9 1.05935
5000 ≈ 9 1.22927
Table 12: Runtime (in seconds) n1 = 0.8 e n2 = 0.2.
CLONALG-HMM
max it Time (s) Standard Deviation
10 0.13173 0.13575
50 0.10288 0.01637
100 0.08619 0.01572
500 0.11110 0.02962
1000 0.10138 0.01722
5000 0.14287 0.02120
Table 13: Number of patterns n1 = 0.8 e n2 = 0.2.
CLONALG-HAMMING
max it Patterns (average) Standard Deviation
10 ≈ 8 0.69921
50 ≈ 8 1.07497
100 ≈ 9 0.78881
500 9 0.81650
1000 ≈ 9 1.19722
5000 ≈ 8 1.33749
Table 14: Runtime (in seconds) n1 = 0.8 e n2 = 0.2.
CLONALG-HAMMING
max it Time (s) Standard Deviation
10 0.26571 0.17477
50 0.23452 0.04880
100 0.26310 0.04446
500 0.24691 0.04951
1000 0.26617 0.03496
5000 0.28276 0.03237
Table 15: Number of patterns n1 = 0.9 e n2 = 0.1.
CLONALG-HMM
max it Patterns (average) Standard Deviation
10 ≈ 8 1.42984
50 ≈ 9 0.69921
100 9 1.24722
500 ≈ 9 0.82327
1000 ≈ 9 1.31656
5000 ≈ 9 0.69921
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
802

Table 16: Runtime (in seconds) n1 = 0.9 e n2 = 0.1
CLONALG-HMM
Execution max it Time (s) & Standard Deviation
10 0.16282 0.22475
50 0.10084 0.01539
100
0.09575 0.02305
500 0.09095 0.01779
1000 0.11448 0.03287
5000 0.12337 0.02006
Table 17: Number of patterns n1 = 0.9 e n2 = 0.1.
CLONALG-HAMMING
max it Patterns (average) Standard Deviation
10 ≈ 8 0.78881
50 ≈ 9 0.84984
100 ≈ 9 0.91894
500 ≈ 8 0.63246
1000 ≈ 9 0.94868
5000 ≈ 8 0.96609
greater attention towards the use of the CLONALG
approach in Bioinformatics.
The graph in Figure 6 shows the execution time
according to the iterations, in which it is possible to
observe that when n1 = 0.6 and n2 = 0.4 for 10 it-
erations the execution time was one of the smallest,
and as the iterations increased the time also increased
when analyzing the samples together. The same anal-
ysis applied to n1 = 0.7 and n2 = 0.3 allows us to
state that the time for 10 iterations was less than the
first case, in the iteration 1000 was superior. Repeat-
ing this evaluation for all samples, taking iteration
10 and 1000 as a reference, we have an interesting
behavior, which is a slight tendency as the n2 de-
creases and the iterations increase, the execution time
decreases. It is not the objective of this work to evalu-
ate this behavior, since efforts were dedicated to find-
ing patterns with the combination of the two algo-
rithms already demonstrated (CLONALG-MMO) in
a way that was unprecedented in Bioinformatics un-
til then, which brought good results, and a range of
new ones programming strategy options, however, in
future works tests may be carried out to assess such
behavior.
The graph in Figure 7 shows the number of pat-
Table 18: Runtime (in seconds) n1 = 0.9 e n2 = 0.1
CLONALG-HAMMING
max it Time (s) Standard Deviation
10 0.22105 0.07671
50 0.27023 0.05026
100 0.25076 0.03600
500 0.25832 0.02078
1000 0.24824 0.05242
5000 0.27329 0.05595
Figure 6: Time graph by iterations CLONALG-HMM.
Figure 7: Pattern number graph by iterations CLONALG-
HMM.
terns found in relation to the iterations, which has a
similar behavior from iteration 50 onwards. Some
optimizations in the mutation method, for example,
can bring improvements in the discovery of patterns,
as may increase the chance of generating an antibody
with higher affinity.
5 CONCLUSIONS
In this work, concepts relevant to biology and bioin-
formatics were addressed, in addition to presenting
applications of approaches related to pattern recogni-
tion. In this context, some deterministic and stochas-
tic pattern recognition methods were analyzed with
examples of both.
According to the works analyzed, it is possible
to notice combinations of several strategies that aim
to improve the quality of pattern recognition. In the
development of this work, it was possible to observe
the effort to offer computational strategies with high
performance that meet the expectations of biologists.
Therefore, it is believed that with the strategies used
in this work it was possible to offer a hybridization
capable of creating patterns with biological quality.
By joining the bioinspired algorithm (CLON-
ALG) with the stochastic algorithm (HMM), it was
possible to extract the best of both, the generated pat-
Pattern Recognition in Biosequences Using Artificial Immune System
803

terns correspond to the patterns found by D’Angelo
and Palmieri (2020). Finally, it is evident that the
strategies used serve as a source of studies for fu-
ture work, which can now rely on the CLONALG
approach, still little explored in the context of Bioin-
formatics, but that through this work its efficiency is
proven.
It is intended in the future to validate the hypoth-
esis of using another mutation approach, to try to
increase the convergence of the algorithm and con-
sequently decrease the execution time. Another ob-
jective is to test the algorithm with parameter n2 in-
versely proportional to the number of iterations, since
the graph in Figure 6 presents an interesting behavior
of the data, where there is a slight tendency to de-
crease of runtime.
Another point that will be addressed is the paral-
lelization of the pattern recognition process, as there
is no data dependency during the iterations, that is,
it is possible to isolate each subsequence with the set
of input sequences, and thus it is possible to evaluate
several subsequences by same time.
ACKNOWLEDGEMENTS
The authors would like to thank S
˜
ao Paulo Research
Foundation (FAPESP) for the financial support, un-
der grants, 20/08615-8, 23/13399-0, 23/13576-0,
23/13610-3, and Coordenac
˜
ao de Aperfeic¸oamento
de Pessoal de N
´
ıvel Superior - Brasil (CAPES) for
the partial financial support.
REFERENCES
Aftabuddin, M. and Kundu, S. (2007). Hydrophobic, hy-
drophilic, and charged amino acid networks within
protein. Biophysical journal, 93(1):225–231.
da Cruz,
´
A. N., Gomes, V., Andrade, M., Amorim, A.,
Val
ˆ
encio, C., Vaughan, G., and Zafalon, G. (2023).
Optimization of snp search based on masks using
graphics processing unit. In Proceedings of the 25th
International Conference on Enterprise Information
Systems - Volume 2: ICEIS, pages 134–141. IN-
STICC, SciTePress.
D’Angelo, G. and Palmieri, F. (2020). Discovering genomic
patterns in sars-cov-2 variants. International Journal
of Intelligent Systems, 35(11):1680–1698.
Dasgupta, D., Yu, S., and Nino, F. (2011). Recent advances
in artificial immune systems: models and applications.
Applied Soft Computing, 11(2):1574–1587.
De Castro, L. N. (2006). Fundamentals of natural com-
puting: basic concepts, algorithms, and applications.
Chapman and Hall/CRC.
Dill, K. A., Bromberg, S., Yue, K., Chan, H. S., Ftebig,
K. M., Yee, D. P., and Thomas, P. D. (1995). Prin-
ciples of protein folding—a perspective from simple
exact models. Protein science, 4(4):561–602.
Fefelova, I., Fefelov, A., Voronenko, M., Kornelyuk, A.,
Sachenko, A., Ryzhkov, E., and Lytvynenko, V.
(2020). Predicting the protein tertiary structure by
hybrid clonal selection algorithms on 3d square lat-
tice. In 2020 IEEE 15th International Conference on
Advanced Trends in Radioelectronics, Telecommuni-
cations and Computer Engineering (TCSET), pages
965–968. IEEE.
Hirst, J. D. (1999). The evolutionary landscape of
functional model proteins. Protein Engineering,
12(9):721–726.
Horn, J., Goldberg, D. E., and Deb, K. (1994). Implicit
niching in a learning classifier system: Nature’s way.
Evolutionary Computation, 2(1):37–66.
Kucherov, G. (2019). Evolution of biosequence search algo-
rithms: a brief survey. Bioinformatics, 35(19):3547–
3552.
Luo, W., Lin, X., Zhu, T., and Xu, P. (2019). A clonal
selection algorithm for dynamic multimodal function
optimization. Swarm and Evolutionary Computation,
50:100459.
Sun, Y. and Buhler, J. (2007). Designing patterns for profile
hmm search. Bioinformatics, 23(2):e36–e43.
Yavuz, B. C¸ ., Yurtay, N., and Ozkan, O. (2018). Predic-
tion of protein secondary structure with clonal selec-
tion algorithm and multilayer perceptron. IEEE Ac-
cess, 6:45256–45261.
ICEIS 2025 - 27th International Conference on Enterprise Information Systems
804