A Solution Procedure for Fixed Mammography Unit Location-Allocation

and Mobile Mammography Unit Routing Problems

Romário dos S. L. de Assis

1,4 a

, Marcos V. A. de Campos

1,2 b

, Marcone J. F. Souza

1,3 c

Maria A. L. Souza

4 d

, Eduardo C. de Siqueira

5 e

, Elizabeth F. Wanner

1,6 f

and Sérgio R. de Souza

1 g

Federal Center of Education Technology of Minas Gerais (CEFET-MG), Brazil

Federal Institute of Education, Science and Technology of Minas Gerais (IFMG), Brazil

Federal University of Ouro Preto (UFOP), Brazil

Federal University of Viçosa (UFV), Brazil

Federal Institute of Education, Science and Technology of Brasília (IFB), Brazil

Aston University, U.K.

Keywords:

Mammography Unit Location-Allocation Problem, Mobile Mammography Unit Routing Problem, Facility

Location.

Abstract:

This paper addresses the Mammography Unit Location-Allocation and Mobile Mammography Unit Routing

problems. The objective is to maximize coverage of the target population and cover unmet demand with ﬁxed

mammography units by using mobile units. It is proposed a sequential solution procedure for solving, in

which the ﬁrst problem is solved by using an exact method, and the second one through a heuristic algorithm

with the uncovered municipalities from the ﬁrst problem as input. This proposal was tested in three scenarios

from the State of Minas Gerais, Brazil. The results show that the coverage of this state can be fully met with

84 additional mobile units, considering the current location of the ﬁxed equipment and the restriction of the

municipalities’ service to their healthcare micro-regions. However, if this requirement is not imposed, 42 units

are sufﬁcient. Finally, by allowing the equipment to be relocated, only nine units are needed.

1 INTRODUCTION

Breast cancer is, after skin cancer, the most com-

mon type of cancer in Brazil. According to (INCA,

2023), 73,610 new cases were estimated in the coun-

try in 2023, and that disease was responsible for

18,139 deaths in 2021. In 2022, statistics presented by

(IARC, 2024), on a global scale, show that consider-

ing both sexes, breast cancer accounted for 11.5% of

the cases, second only to lung cancer. When consider-

ing only the female population, the incidence reaches

23.8%, ranking ﬁrst.

https://orcid.org/0000-0002-5726-5910

https://orcid.org/0000-0002-5599-8889

https://orcid.org/0000-0002-7141-357X

https://orcid.org/0009-0001-4290-0061

https://orcid.org/0009-0001-2093-2783

https://orcid.org/0000-0001-6450-3043

https://orcid.org/0000-0001-7831-6740

The most effective way to detect the disease is

through mammography screening (Azevedo et al.,

2019). According to (Ramos et al., 2018), when

coverage exceeds 70% of the target group, mortal-

ity among women aged 50 years and older is reduced

by 20% to 30%. However, mammography cover-

age rates vary signiﬁcantly from one country to an-

other, from one city to another, or even within re-

gions of the same state. As an example, (Lages et al.,

2012) described that, between 2010 and 2011, the

access of women to screenings in Teresina, State of

Piauí, Brazil, was higher than in cities like Rio de

Janeiro, Recife, João Pessoa, and other municipali-

ties in Brazil. Teresina’s coverage also surpassed that

of Turkey, where 56% of individuals are unaware of

the exam, Mexico, where the coverage during this bi-

ennium was only 14.8%, and Australia, where 49%

of women aged 40 to 49 have never undergone the

exam. However, the study shows that, despite having

L. de Assis, R. S., A. de Campos, M. V., Souza, M. J. F., Souza, M. A. L., C. de Siqueira, E., Wanner, E. F. and R. de Souza, S.

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems.

DOI: 10.5220/0013293700003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 523-533

ISBN: 978-989-758-749-8; ISSN: 2184-4992

523

a higher coverage than many municipalities in Brazil

and worldwide, the coverage was only 62.1%, below

the 70% suggested by (Ramos et al., 2018). This work

also shows that more than half of the equipment in the

Northeast region is installed in the capitals. Thus, the

poor distribution of equipment is one of the reasons

the coverage does not reach the desired percentage.

This fact is also demonstrated by (Corrêa et al., 2011),

as the authors state that the poor distribution of mam-

mography units directly impacts the low production

of the equipment. In addition to inadequate distribu-

tion, (Corrêa et al., 2011) point out that, for women

who need to travel, the distance traveled is one of

the factors inﬂuencing their decision to undergo the

exam. The authors also state that, in 2015, the Min-

istry of Health established a maximum distance of 60

km to be traveled to perform the exam.

The Mammography Unit Location-Allocation

Problem (MULAP) is proposed in light of these is-

sues, such as the inefﬁcient distribution of the mam-

mography units, the signiﬁcant impact of women’s

travel on coverage rates, and the importance of this

exam for successful disease treatment. The MULAP

objective is to improve the location of mammography

units and, thus, increase the coverage rate of mam-

mography exams. (Souza et al., 2019) used two math-

ematical formulations to solve MULAP. In one, full

demand fulﬁllment for municipalities is considered,

while the second formulation allows for partial de-

mand fulﬁllment. In the conducted experiments, sce-

narios were considered where the existing mammog-

raphy units were kept in their current locations and

scenarios where there was the possibility of relocat-

ing those equipment. The results showed that relo-

cating the equipment would result in greater coverage

than that presented by the State Health Department of

Rondônia, Brazil. (Sá et al., 2019), using the formu-

lation of (Souza et al., 2019), addressed MULAP in

an instance of the State of Espírito Santo, considering

two scenarios: one keeping the existing location and

the other allowing the relocation of the mammogra-

phy units. The authors showed that the existing loca-

tion met half of the state’s demand, using 63.1% of

the capacity of the mammography units, while relo-

cating the equipment would allow for 83.5% demand

coverage, increasing the equipment usage to 99.9%.

(Souza et al., 2020) used the same model and devel-

oped a Variable Neighborhood Search (VNS) algo-

rithm to solve an instance based on data from the State

of Minas Gerais. In this case, the results obtained,

both from the mathematical formulation and the pro-

posed algorithm, showed superior coverage compared

to the existing location of the mammography units.

(de Campos et al., 2020) addressed MULAP using a

Simulated Annealing algorithm. The algorithm was

applied to instances from the state of Minas Gerais,

considering partial demand fulﬁllment. In this way,

a municipality is covered even if its demand is not

fully met. Additionally, that work considered the ac-

quisition of new equipment. The results indicated

that, even under these conditions, not all municipal-

ities had their demands fully met. Other studies in the

literature, such as (de Assis et al., 2022), (de Cam-

pos et al., 2022), and (de Campos et al., 2024), also

address MULAP. In all these works, full demand cov-

erage is not achieved due to factors such as the max-

imum distance constraint between the demand point

and the equipment’s host municipality and/or the ab-

sence of hospital infrastructure.

(Jewett et al., 2018) showed that the demand for

the screenings is inversely proportional to the dis-

tance traveled to perform it. In this sense, (De Mil

et al., 2019) suggested using Mobile Mammography

Units (MMU) to serve women living in remote areas

where the installation of a ﬁxed unit is unfeasible.

(Rosa et al., 2020) proposed a constructive heuristic

algorithm to address the Mobile Mammography Unit

Routing Problem (MMURP). In (Rosa et al., 2020),

MMUs were routed to serve 444 locations, aiming to

maximize the coverage of the demand and minimize

the total distance traveled. In (Rosa et al., 2021), the

authors presented an Iterated Greedy Search (IGS) al-

gorithm to route 56 MMUs, departing from two de-

pots, to serve 579 municipalities.

The aforementioned studies addressed MULAP

and MMURP separately. In the present work, the ob-

jective is to solve them through a sequential proce-

dure. Initially, it is proposed to generate a solution

for MULAP and then, based on the municipalities not

served or partially served in this solution, generate a

solution via MMURP. To solve these two problems,

the formulation by (Souza et al., 2019) will be ap-

plied for the solution of MULAP, and based on the re-

sults obtained, a constructive heuristic algorithm will

be applied to route the MMUs to meet the remaining

demand from MULAP. This solution procedure is ap-

plied to a case study addressing three scenarios in the

State of Minas Gerais. The ﬁrst scenario considers the

freedom to relocate ﬁxed mammography equipment.

The second scenario considers the current location of

ﬁxed equipment and does not restrict the service of

municipalities to their health micro-regions. Finally,

the third scenario considers the current location of

ﬁxed equipment and restricts the service of munici-

palities to their health micro-regions.

The remainder of this work is organized as fol-

lows. Section 2 describes the problems addressed.

Section 3 presents the application scenarios for MU-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

524

LAP, as well as the main proposed changes in the

mathematical formulation to meet the characteristics

of these scenarios. Section 4 presents the construc-

tive algorithm for MMURP. Finally, Sections 5 and 6

present the results achieved, conclusions, and indica-

tions for future work.

2 PROBLEM

CHARACTERIZATION

This section is organized as follows. Subsection 2.1

presents the mathematical formulation of the MULAP

problem used by (Souza et al., 2019) and an example

illustrating this problem. In Subsection 2.2, the char-

acteristics of the MMURP are presented along with

an example.

2.1 Mammography Unit Location and

Allocation Problem – MULAP

Table 1 describes the notation, parameters, and auxil-

iary and decision variables of the mathematical for-

mulation for MULAP introduced by (Souza et al.,

2020), which is given by:

max

∑

i∈N

∑

j∈S

dem

· x

i j

(1)

s. a

∑

i∈S

i j

≤ 1, ∀ j ∈ N (2)

∑

i∈N

= p (3)

∑

j∈S

dem

· x

i j

≤ cap · y

, ∀i ∈ N (4)

≥

, ∀i ∈ N (5)

≥ x

i j

, ∀i, j ∈ N (6)

= z

, ∀i ∈ N (7)

= 0, ∀i ∈ N | Infra

= 0 (8)

i j

∈ [0, 1], ∀ i, j ∈ N (9)

∈ Z

, ∀ i ∈ N (10)

∈ {0, 1}, ∀ i ∈ N (11)

The objective function (1) aims to maximize

the coverage of the mammography demand. Con-

straints (2) ensure that the demand of each munici-

pality j, if covered, is partially met by mammography

units installed in municipalities within R km from it.

Constraint (3) ensures that all p available units are

installed. Constraints (4) ensure that the annual ca-

pacity of each mammography unit is respected. Con-

straints (5) force z

to equal 1 if at least one unit is

installed in municipality i. Constraints (6) ensure that

a municipality j’s demand can only be covered by a

municipality i if there is a unit in that municipality.

Constraints (7) state that if a municipality i has mam-

mography units, all its own demand must be covered

by its own units. Constraints (8) indicate that only

municipalities with hospital infrastructure can host

mammography units. Finally, constraints (9), (10),

and (11) deﬁne the domain of the decision variables.

Figure 1 shows an example of the MULAP with

10 municipalities (A, B, C, D, E, F, G, H, I, J),

each with a demand dem for mammography screen-

ings. To meet this demand, there are 3 mammography

units (M1, M2, M3) with a ﬁctitious capacity of 1000

screenings annually, which can be installed in munic-

ipalities A, E, and H, as they have the infrastructure

to host them. The lines connecting the municipali-

ties indicate the distances between them. Note that

mammography units M1 and M2 are installed in mu-

nicipality A, and M3 is installed in H. Unit M1 fully

meets the demand of municipality A, and the surplus

covers the demand of municipalities B, D, and part of

municipality C. Unit M2 covers the unmet demand of

municipality C. Unit M3 fully meets the demand of

municipalities H, I, and J, and partially meets the de-

mand of municipality F. Although unit M2 has a non-

used capacity of 950 mammography screenings, these

screenings cannot meet the demand of municipality E,

as it is located 90 km from municipality A, violating

the maximum travel distance R of 60 km. Thus, the

location of the mammography units in this scenario

allows coverage of 2,050 women, with an unmet de-

mand of 950 mammography screenings.

2.2 Mobile Mammography Unit

Routing Problem – MMURP

Let there be a set of host municipalities, which are

the starting points for a set of Mobile Mammography

Units (MMUs), and a set of municipalities with a de-

mand for mammography screenings. MMURP, intro-

duced by (Rosa et al., 2020), consists of determining

the routes of the MMUs to meet all the demands for

mammography screenings while minimizing the total

distance traveled.

The approach presented here considers that the

starting point for each MMU is the reference munic-

ipality of each health macro-region, thus deﬁning a

multi-depot vehicle routing problem. In addition, the

MMURP is treated based on the variant described by

the Open Vehicle Routing Problem (OVRP), as pre-

sented in (Li et al., 2007), considering that the return

of the MMU to the starting point should not be in-

cluded. A maximum distance restriction of D

max

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems

525

Table 1: Parameters and decision variables.

Parameters

N set of municipalities

i j

distance from municipality i to municipality j

dem

demand for screenings from municipality j

cap annual capacity of a mammography unit

p number of mammography units to be located

R maximum distance a woman can travel

Infra

binary parameter that equals 1 if municipality i has

hospital infrastructure, 0 otherwise

set of municipalities that are at most R km from municipality i,

that is, S

= { j ∈ N | d

i j

≤ R and d

≤ R}

Auxiliary variables

binary variable equal to 1 if a mammography unit is installed in

municipality i and 0 otherwise

i j

Continuous variable in the range [0, 1] that indicates the fraction

of the demand of municipality j met by mammography units

installed in municipality i.

Integer variable representing the number of mammography units

installed in municipality i

90 km

B C D

59 km

15 km

48 km

57 km

12 km

45 km

37 km

75 km

30 km

42 km

dem: 150

dem: 600

M1: 150

dem: 150

M1: 100

M1: 150

M2: 50

M1: 600

dem: 200

dem: 150 dem: 150

M3: 150 M3: 150

M3: 100

dem: 700

dem: 600

dem: 150

M3: 600

Figure 1: Example of location-allocation of mammography units.

between one municipality and another on the route is

also deﬁned.

For example, considering an MMU speed of 60

km/h, if D

max

= 180 km and the trip starts in the

morning, it is possible to carry out mammography

screenings in the destination municipality on the same

day. This maximum distance restriction does not ap-

ply to MMUs leaving their departure points. Finally,

a capacity of 4 mammography screenings per hour in

each MMU is also considered.

To illustrate the MMURP, consider Figure 2,

which presents the situation in the State of Rondônia

after applying the MULAP. The municipalities shown

in white color were fully covered by ﬁxed mammog-

raphy units, while those in green color had their de-

mand only partially covered. The set of municipalities

{A, B, C, D, E, F, G} are those whose demand was

not fully met by MULAP, and the set {1, 2, 3, 4} in-

cludes the municipalities with hospital infrastructure.

In this case, the problem is to determine the number of

MMUs needed to serve the demand of municipalities

A, B, C, D, E, F, and G, starting from municipalities

1, 2, 3, and/or 4 and covering the shortest possible

distance.

In the scenario represented in Figure 2, detailed in

Figure 3, three new routes are established to cover the

demand of municipalities that were not fully served

by the ﬁxed mammography units, identiﬁed in green.

There is one route departing from Municipality 1,

covering Municipalities A, B, and C; another route

departing from Municipality 2 and covering Munic-

ipalities D and E; and, ﬁnally, a third route starting

from Municipality 3 and covering Municipalities F

and G.

To illustrate the time required to complete each

route, consider in Figure 3 that each MMU is capa-

ble of performing 6758 mammography screenings an-

nually. Furthermore, assume that the number above

the arrow between the base of an MMU and a mu-

nicipality, or between two municipalities, represents

the travel time. Also consider that the ﬁrst number

in brackets, above each municipality, represents the

setup time, and the second number indicates the re-

quired time to perform all the screenings in the mu-

nicipality under consideration. Regarding the setup

time, a value of zero indicates that there is no setup

time, a situation that occurs when the MMU arrives at

the end of the day.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

526

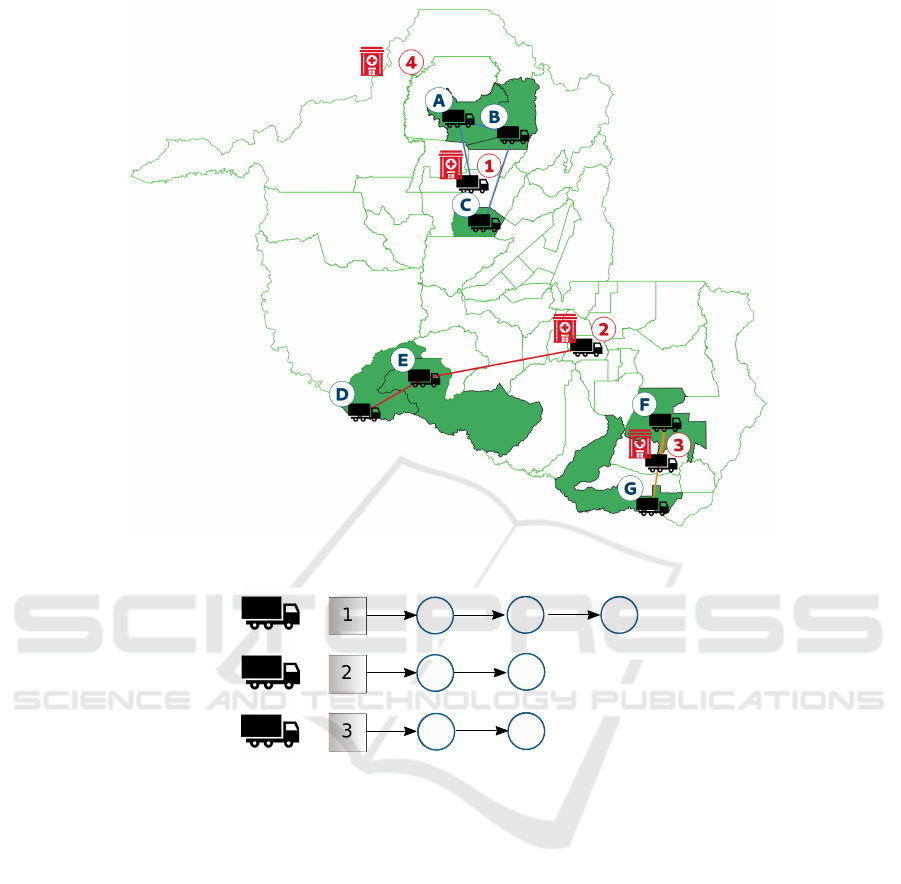
Figure 2: Example of MMU routing: situation in the State of Rondônia after applying the MULAP.

30 60

[60][2220]

[0][2280]

[60][2400]

[60][3000]

[0][1500]

[60][1000]

[60][2000]

Figure 3: Routing relative to Figure 2.

3 A SOLUTION FOR MULAP

The main works in the literature for solving MULAP

use the formulation proposed by (Souza et al., 2019).

The current work also uses that formulation. In this

article, three scenarios are considered. Scenario 1 al-

lows the relocation of mammography units, and the

assignment of exams is made without considering the

health micro-regions. In Scenario 2, the current lo-

cation of the equipment is kept; however, the assign-

ment of exams does not observe the micro-regions.

Scenario 3, in turn, maintains the current location of

the equipment and respects the health micro-region of

the municipalities.

To meet the requirements of Scenarios 2 and 3

and prevent the mammography units from being relo-

cated, the set of constraints (12) is added, as follows:

≥ pe

∀i ∈ N. (12)

where pe

represents the number of mammography

units installed in municipality i. To meet Scenario 3, it

is also necessary to restrict the service of a municipal-

ity to the health micro-region it belongs to. Thus, it is

necessary to update S

to include only the municipal-

ities whose distances to municipality i are less than

or equal to R km and are in the same health micro-

region. In this case:

= { j ∈ N | d

i j

≤ R and d

≤ R and reg

= reg

4 PROPOSED ALGORITHM FOR

MMURP SOLUTION

The solution for MMURP proposed in this work is

based on the construction phase of the GRASP meta-

heuristic, where a restricted candidate list with the α

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems

527

best candidates is generated. At each iteration, an el-

ement is randomly selected from this restricted list of

the best candidates and inserted into the solution. The

method developed is described by Algorithms 1 and 2.

Algorithm 1: buildMMURPSolution (CL, α).

Data: CL: List of cities, α: Parameter to control the greediness

Result: s: Solution generated

1 s ←

0 ; // Solution to be generated

2 j ← 1 ; // Route counter

3 R

←

0 ; // Initial route

4 newRoute ← T RUE

5 while CL ̸=

0 do

6 if newRoute then

7 StartNewRoute(j, R, s, CL, newRoute) ; // Starts a

new route.

8 else

9 RCL ← generateRestrictedCandidateList(CL, α)

10 i ← Randomly chosen city from RCL

11 R

← Add city i to route R

12 Update the time of route R

13 Update the demand of city i

14 if Time of R

reached the limit then

15 s ← Add route R

to the solution s

16 j ← j + 1

17 newRoute ← T RUE

18 else

19 newRoute ← FALSE

20 end

21 if i has no demand left then

22 CL ← CL \ {i}

23 end

24 end

25 end

26 return s

Lines 1 to 4 of Algorithm 1 initialize the method

variables. Lines 5-25 construct the solution by insert-

ing a municipality at each iteration while there are still

municipalities in the Candidate List (CL) to be served.

Line 7 creates a new route to be added to the solu-

tion when necessary, as described by Algorithm 2. In

lines 8-24, cities are added to the current route ac-

cording to the number of exams to be performed. In

line 9, a Restricted Candidate List (RCL) is generated

with the α municipalities from CL closest to the last

city added to the route. In line 10, a city is randomly

selected from the RCL, and in lines 11-13, this city is

added to the route, updating the route’s time and the

demand of this city. The route time update involves

calculating the time spent attending to the municipal-

ity’s demand, including travel and preparation time.

The demand update determines how many screenings

can be performed within one year. In lines 14-20, it

is veriﬁed whether the MMU’s capacity (route time)

is exhausted after adding a new municipality to the

route. If so, the route is added to solution s, and the

newRoute variable is set to TRUE. Finally, in lines 21-

Algorithm 2: StartNewRoute( j, R, s, CL, newRoute).

Data: CL: List of municipalities, j: Route counter, R: Routes, s:

Solution, newRoute: Indicates if it’s a new route

Result: newRoute: Returns whether a new route should be

started

1 i ← Municipality with the highest demand in CL

2 D ← closest depot to municipality i

3 if D ∈ CL then

4 R

← Add depot D to route R

5 Update the time of R

6 Update the demand of D

7 if Time of R

reached the limit then

8 s ← Add route R

to the solution s

9 j ← j + 1

10 newRoute ← T RUE

11 if D has no demand left then

12 CL ← CL \ {D}

13 end

14 else

15 R

← Add city i to route R

16 Update the time of R

17 Update the demand of i

18 if Time of R

reached the limit then

19 s ← Add route R

to the solution s

20 j ← j + 1

21 newRoute ← T RUE

22 else

23 newRoute ← FALSE

24 end

25 if i has unmet demand then

26 CL ← CL \ {i}

27 end

28 end

29 else

30 R

← Add depot D to route R

31 R

← Add city i to route R

32 Update the time of R

33 Update the demand of i

34 if Time of R

reached the limit then

35 s ← Add route R

to the solution s

36 j ← j + 1 newRoute ← T RUE

37 else

38 newRoute ← FALSE

39 end

40 if i has no demand left then

41 CL ← CL \ {i}

42 end

43 end

44 return newRoute

23, the selected municipality is removed from CL if

its demand is fully met.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

528

Algorithm 2, in turn, describes the procedure for

opening new routes. In lines 1 and 2, the municipal-

ity i with the highest demand is used to determine the

depot for the new route, which is the closest to this

municipality i. The steps described in lines 3 to 43 of

Algorithm 2 are very similar to the steps previously

described in Algorithm 1. These lines insert cities

into the route, update times and demands, and, if nec-

essary, close the route.

5 RESULTS

The mathematical formulation was executed using

the CPLEX solver, version 20.1. The constructive

MMURP algorithm, in turn, was implemented in C++.

The experiments were conducted on a DELL Inspiron

153511 laptop, with an Intel Core i7-1165G7 proces-

sor, 16 GB of RAM, and Ubuntu 20.04 Operating

System.

The instances used in this work utilize population

data from the 2022 Brazilian Census. The group of

candidate municipalities to host the equipment con-

sists of municipalities that currently have hospitals

and/or host mammography units in the existing con-

ﬁguration. The number of available mammography

units was obtained from the DATASUS system in De-

cember 2023.

The experiments considered three distinct scenar-

ios. The ﬁrst scenario assumes there is freedom to re-

locate mammography units. The second scenario con-

siders that mammography units must remain at their

current locations, serving any municipalities located

up to 60 km away. The third scenario differs from the

previous one in terms of target population coverage;

in this scenario, coverage is restricted to municipali-

ties within the same health micro-region.

For the constructive MMURP algorithm, in-

stances were formed using data from municipalities

not covered by the MULAP solution. Additionally,

these instances consider the reference municipalities

for each health macro-region in the State as depots.

Furthermore, for each scenario, two values for the

maximum distance traveled were tested: 180 km, as

proposed by (Rosa et al., 2020), and 545 km, to eval-

uate the consequence of relaxing this maximum dis-

tance traveled.

Table 2 reports the results obtained from apply-

ing the mathematical formulation to the MULAP. The

ﬁrst and second columns consist of the identiﬁer and

description of each analyzed scenario, respectively.

The third and fourth columns show, respectively, the

number and rate of exams covered by the MULAP.

Finally, the ﬁfth and sixth columns show, in this or-

der, the number and rate of demand not covered by

the MULAP.

As can be observed in Table 2, as the restrictions

in the MULAP increase, the demand coverage rate de-

creases. In the ﬁrst scenario, the coverage approaches

totality, considering the freedom to relocate the equip-

ment. In the second and third scenarios, while pre-

serving the current mammography unit locations, the

coverage rate decreases substantially. By restricting

the service of a municipality to its health micro-region

(third scenario), this rate falls to 72.08%. These re-

sults show that the current location-allocation of the

mammography units in the State of Minas Gerais is

inefﬁcient, and the conﬁguration of the health micro-

regions in the state further limits the coverage of the

demand.

Table 3 reports the results obtained by applying

the constructive algorithm to the MMURP. The ﬁrst

column presents the ID of the scenario analyzed in the

MULAP and the maximum distance traveled between

two cities in MMURP; the second column reports the

number of MMUs required to meet the remaining de-

mand for each of these scenarios; the third column

displays the total distance traveled by the MMUs; the

fourth column presents the total demand covered by

the MMUs, and, ﬁnally, the ﬁfth and sixth columns

show, respectively, the average occupancy and the oc-

cupancy rate of the MMUs.

As can be observed in Table 3, the remaining de-

mand from the MULAP in Scenario 1 is fully met

by 9 MMUs, which travel 2164 km. The remaining

demand in the second Scenario requires 42 MMUs,

covering a total of 14937 km to perform 182754 ex-

ams, while the remaining demand in the third Sce-

nario is covered by 84 MMUs, which travel a total of

30578 km, serving 484987 patients. Considering that

an MMU can serve 6758 patients, Scenario 3 made

the best use of its capacity, achieving an average uti-

lization of 85.42%. On the other hand, in Scenario 1,

due to the geographical locations of the served mu-

nicipalities and the maximum distance restriction im-

posed on the MMU between cities, the average uti-

lization reached a rate of 17.15%.

Illustrating a solution for the MULAP, Table 4

presents the routes of the MMUs required to meet

the remaining demand in scenario blue1. The ﬁrst

column identiﬁes the route of each MMU described

in the second column, while the third and fourth

columns report, in this order, the distance traveled by

each and the demand covered by them.

As can be observed in Table 4, to meet the remain-

ing demand from the MULAP in Scenario 1, Algo-

rithm 1 generated a solution with 9 MMUs needed to

cover the target population. These 9 MMUs cover a

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems

529

Table 2: Characteristics of the MULAP solution for the State of Minas Gerais.

ID Scenario Demand Covered Coverage Rate Remaining Demand Uncovered Rate

1 Freedom to relocate and allocate 1,728,037 99.40% 10,435 0.60%

2 Maintains current location, changes

allocation

1,555,710 89.49% 182,754 10.51%

3 Maintains current location, imposes

health micro-region

1,253,482 72.08% 484,987 27.92%

Table 3: Characteristics of the MMURP solution of the State of Minas Gerais.

Scenario # Routes Total Total Average MMU

Distance Traveled Demand Covered MMU Occupation Occupation Rate

1 (180 km) 9 2,164 10,435 1,159 17.15%

2 (180 km) 42 14,937 182,754 4,351 64.38%

3 (180 km) 84 30,578 484,987 5,773 85.42%

1 (545 km) 2 3,339 10,435 5,217.5 77.20%

2 (545 km) 29 17,020 182,754 6,301.9 93.25%

3 (545 km) 74 32,392 484,987 6,553.9 96.98%

Table 4: Detailed solution of the MMURP in Scenario 1 (180 km).

ID Route Distance (km) Coverage

1 Patos de Minas → Brasilândia de Minas → Dom Bosco → Natalândia 364 1,549

2 Diamantina → Buenópolis → Joaquim Felício → Augusto de Lima → Santo

Hipólito → Monjolos → Santana de Pirapama → Santana do Riacho

429 3,025

3 Teóﬁlo Otoni → Novo Oriente de Minas 71 728

4 Teóﬁlo Otoni → Mata Verde 345 631

5 Montes Claros → Claro dos Poções → Jequitaí → Francisco Dumont → Ib-

iaí → Santa Fé de Minas

362 2,279

6 Patos de Minas → São Gonçalo do Abaeté → Varjão de Minas 139 1,020

7 Governador Valadares → São Geraldo da Piedade → São José da Saﬁra 167 585

8 Montes Claros → Itacambira 99 313

9 Montes Claros → Padre Carvalho 188 305

Total 2,164 10,435

Table 5: Detailed solution of the MMURP in Scenario 1 (545 km).

ID Route Distance (km) Coverage

1 Patos de Minas → Brasilândia de Minas → Dom Bosco → Natalândia → Santa

Fé de Minas → Ibiaí → Jequitaí → Francisco Dumont → Claro dos

Poções → Itacambira → Joaquim Felício → Buenópolis → Augusto de

Lima → Santo Hipólito → Monjolos → Santana de Pirapama

1,378 6,657

2 Teóﬁlo Otoni → Novo Oriente de Minas → São José da Saﬁra → São Geraldo

da Piedade → Santana do Riacho → Santana de Pirapama → São Gonçalo do

Abaeté → Varjão de Minas → Padre Carvalho → Mata Verde

1,961 3,778

Total 4,158 10,435

total of 2164 km and serve 10435 patients. The routes

described in Table 4 are graphically presented in Fig-

ure 4. It can be observed that the geographical distri-

bution of the municipalities required a greater number

of MMUs to fully meet the mammography demand.

Table 5, in turn, shows that the ﬂexibility (from 180

to 545 km) of the maximum distance traveled between

two cities reduces the number of necessary routes and,

consequently, increases the occupancy rate of MMUs.

Figure 5 exhibits the routes described in Table 5.

6 CONCLUSIONS

This work addressed the MULAP and MMURP us-

ing a sequential solution procedure. The MULAP

was solved using a mathematical formulation from

the literature and applied to three different scenarios.

In Scenario 1, the possibility of relocating equipment

was considered; in Scenarios 2 and 3, the current lo-

cation of the equipment was kept, and, by turn, in sce-

nario 3, the service of a municipality was restricted to

its health micro-region. The MMURP was addressed

by a constructive algorithm applied to the remaining

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

530

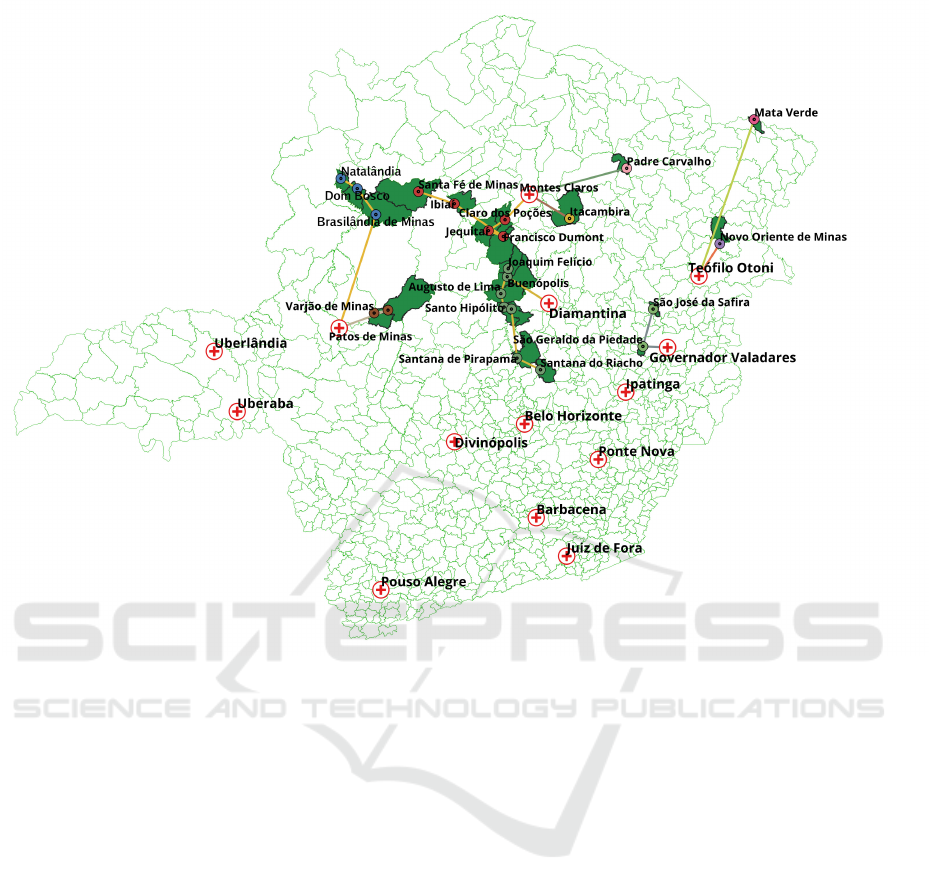
Figure 4: MMURP Routes - Instance MMURP-MG-Flexible.

demand resulting from the MULAP solution.

Among the three scenarios analyzed in the MU-

LAP solution, the result obtained in Scenario 3 had

the lowest coverage, 72.08%, followed by Scenario 2,

with 89.49% of the demand met, and Scenario 1 with

99.40% coverage. These results were expected, once

Scenario 3 represents the situation closest to reality.

In fact, in this scenario, the current location of the

existing equipment is considered, and the obligation

for the target population to be covered only within the

health micro-region to which each municipality be-

longs is imposed. Scenario 2 is somewhat more ﬂexi-

ble since it allows services to be provided outside the

health micro-regions. The result in Scenario 1 shows

that, with the current mammography units, it would

be possible to meet almost all the demand in the State

of Minas Gerais.

Regarding the MMURP, the solution in Scenario 3

was also the worst, requiring 84 MMUs. The solution

in Scenario 1 was the best, requiring only 9 MMUs,

with most of these MMUs making short routes and

serving a small set of municipalities. Many of these

routes depart from the same home municipality to

a single destination municipality due to the distance

limitation imposed on MMUs, which cannot travel

more than 180 km from one municipality to another.

Given this result, the MMURP solution in Scenario 1

could be improved by allowing the distance traveled

between municipalities to be greater. Finally, these re-

sults from the MULAP and MMURP show that when

mammography units are not well-located, coverage is

lower, consequently requiring more MMUs to meet

the demand from uncovered municipalities.

For future work, it is suggested to develop reﬁne-

ment heuristics to reduce the number of MMUs and

make better use of each MMU’s capacity.

ACKNOWLEDGMENTS

The authors register their thanks to Centro Federal

de Educação Tecnológica de Minas Gerais (CEFET-

MG), Universidade Federal de Ouro Preto (UFOP),

Universidade Federal de Viçosa (UFV), Instituto Fed-

eral de Educação, Ciência e Tecnologia de Mi-

nas Gerais (IFMG), Aston University, Instituto Fed-

eral de Educação, Ciência e Tecnologia de Brasília

(IFB), and to the Brazilian agencies Conselho Na-

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems

531

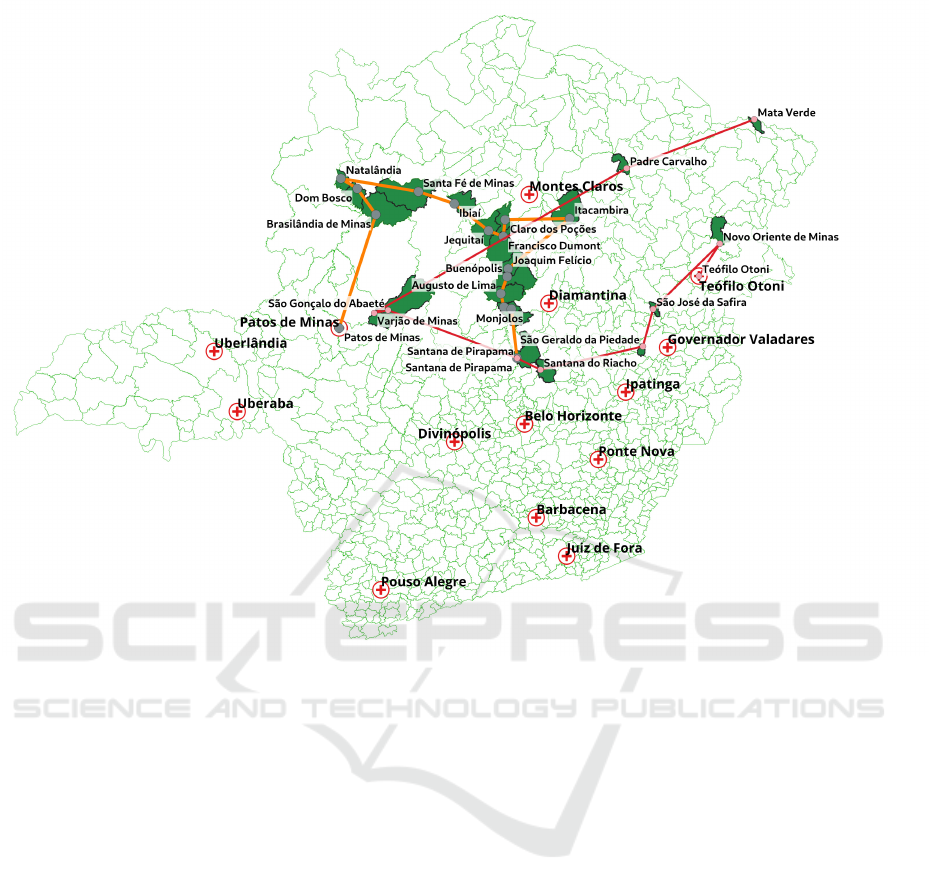
Figure 5: MMURP Routes - Instance MMURP-MG-Flexible.

cional de Desenvolvimento Cientíﬁco e Tecnológico

(CNPq, grants 428817/2018-1, and 311074/2023-5),

Fundação de Amparo à Pesquisa do Estado de Mi-

nas Gerais (FAPEMIG, grant PPM-CEX 676/17),

and Coordenação de Aperfeiçoamento de Pessoal de

Nível Superior (CAPES, ﬁnance code 001 and grant

88881.934148/2024-01) for supporting the develop-

ment of this work.

REFERENCES

Azevedo, A., Ramos, A. L., Gonçalves, A. C. V., Souza, C.

F. d., Batista, G. S., Silva, R. B. V., and Loyola, E. A.

C. d. (2019). O conhecimento de mulheres acerca do

rastreamento do câncer de mama e suas implicações.

Revista de Medicina, 98(3):187–193.

Corrêa, R. d. S., Freitas-Júnior, R., Peixoto, J. E., Ro-

drigues, D. C. N., Lemos, M. E. d. F., Marins, L. A. P.,

and Silveira, É. A. d. (2011). Estimativas da cobertura

mamográﬁca no estado de Goiás, brasil. Caderno de

Saúde Pública, 27(9):1757–1767.

de Assis, R. S. L., de Campos, M. V. A., Souza, M. J. F.,

Silva, M. A. L., de Siqueira, E. C., and de Souza,

S. R. (2022). Um algoritmo variable neighborhood

search para o Problema de Localização de Mamó-

grafos com atendimento parcial. In Anais do LIV Sim-

pósio Brasileiro de Pesquisa Operacional, volume 54,

page 152748, Juiz de Fora, Brasil. Galoá: Campinas.

de Campos, M., Moreira de Sá, M., Rosa, P., Penna, P.,

de Souza, S., and Souza, M. (2020). A mixed lin-

ear integer programming formulation and a simulated

annealing algorithm for the mammography unit loca-

tion problem. In Proceedings of the 22nd Interna-

tional Conference on Enterprise Information Systems.

SCITEPRESS - Science and Technology Publications.

de Campos, M. V. A., de Assis, R. d. S. L., Souza, M. J. F.,

de Siqueira, E. C., Silva, M. A. L., and de Souza, S. R.

(2024). Multi-objective mammography unit location–

allocation problem: A case study. Oper. Res. Health

Care, 41:100430.

de Campos, M. V. A., de Assis, R. S. L., Souza, M. J. F.,

Silva, M. A. L., de Siqueira, E. C., and de Souza, S. R.

(2022). Algoritmos NSGA-II e SPEA2 para o prob-

lema multiobjetivo de localização de mamógrafos. In

Anais do LIV Simpósio Brasileiro de Pesquisa Opera-

cional, volume 54, page 152742, Juiz de Fora, Brasil.

Galoá: Campinas.

De Mil, R., Guillaume, E., Launay, L., Guittet, L., Dejardin,

O., Bouvier, V., Notari, A., Launoy, G., and Berchi,

C. (2019). Cost-effectiveness analysis of a mobile

mammography unit for breast cancer screening to re-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

532

duce geographic and social health inequalities. Value

Health, 22(10):1111–1118.

IARC (2024). Cancer today. International Agency for

Research on Cancer (IARC). https://bit.ly/3XfzYgF

Acessado em 26/04/2024.

INCA (2023). Câncer de mama : vamos falar sobre isso?

Instituto Nacional do Cancer. https://bit.ly/4bXlmqe.

Acesso em 26/04/2023.

Jewett, P. I., Gangnon, R. E., Elkin, E., Hampton, J. M., Ja-

cobs, E. A., Malecki, K., LaGro, J., Newcomb, P. A.,

and Trentham-Dietz, A. (2018). Geographic access to

mammography facilities and frequency of mammog-

raphy screening. Ann. Epidemiol., 28(2):65–71.e2.

Lages, R. B., Oliveira, G. d. P., Simeão Filho, V. M.,

Nogueira, F. M., Teles, J. B. M., and Vieira, S. C.

(2012). Desigualdades associadas à não realização de

mamograﬁa na zona urbana de Teresina-Piauí-Brasil,

2010-2011. Rev. Bras. Epidemiol., 15(4):737–747.

Li, F., Golden, B., and Wasil, E. (2007). The open vehicle

routing problem: Algorithms, large-scale test prob-

lems, and computational results. Computers & Op-

erations Research, 34(10):2918–2930.

Ramos, A. C. V., Alves, L. S., Berra, T. Z., Popolin,

M. P., Arcoverde, M. A. M., Campoy, L. T., Martoreli

Júnior, J. F., Lapão, L. V., Palha, P. F., and Arcêncio,

R. A. (2018). Estratégia saúde da família, saúde su-

plementar e desigualdade no acesso à mamograﬁa no

Brasil. Rev Panam Salud Publica.

Rosa, M. P., Sá, V. S. M., Paiva, J. N. M. Penna, P. H. V.,

and Souza, M. J. F. (2020). Análise da localização

de mamógrafos em Minas Gerais. In LII Simpósio

Brasileiro de Pesquisa Operacional, João Pessoa –

Brasil.

Rosa, O. A. S., ROSA, P. M., PAIVA, J. N. M., Penna,

P. H. V., and Souza, M. J. (2021). Um algoritmo

heurístico baseado em iterated greedy para o prob-

lema de roteamento de unidades móveis de mamo-

graﬁa. In LIII Simp. Bras. de Pesquisa Operacional

(SBPO 2021), João Pessoa – Brasil.

Sá, M. V. S. M., Rosa, P. M., Paiva, J. N. M., SOUZA,

M. J. F., and PENNA, P. H. V. (2019). Localização

de mamógrafos: Um estudo de caso do Estado do Es-

pírito Santo. In XXVI Simpósio de Engenharia de Pro-

dução, Baurú. Universidade Estadual Paulista.

Souza, M. J. F., Penna, P. H. V., Moreira de Sá, M. V. S.,

and Rosa, P. M. (2020). A VNS-based algorithm for

the mammography unit location problem. In Variable

Neighborhood Search, Lecture notes in computer sci-

ence, pages 37–52. Springer International Publishing,

Cham.

Souza, M. J. F., Penna, P. H. V., Stilpen, M., Rosa, P. M.,

Monteiro, J. C., and Lisboa, M. R. (2019). Localiza-

ção de mamógrafos: formulações e estudo preliminar

de caso de Rondônia. In LI Simpósio Brasileiro de

Pesquisa Operacional, Limeira - Brasil.

A Solution Procedure for Fixed Mammography Unit Location-Allocation and Mobile Mammography Unit Routing Problems

533