Leveraging Transfer Learning to Improve Convergence in All-Pay

Auctions

Luis Eduardo Craizer

1 a

, Edward Hermann

1 b

and Moacyr Alvim Silva

2 c

Pontif

ıcia Universidade Cat

olica, 22451-900, Rio de Janeiro, RJ, Brazil

Fundac¸

ao Getulio Vargas, 22250-145, Rio de Janeiro, RJ, Brazil

Keywords:

Transfer Learning, Auction Theory, Nash Equilibrium, Deep Reinforcement Learning, Multi-Agent, All-Pay.

Abstract:

In previous research on Multi-Agent Deep Deterministic Policy Gradient (MADDPG) in All-Pay Auctions,

we identiﬁed a key limitation: as the number of agents increases, the tendency for some agents to bid 0.0 —

resulting in local equilibrium — grows, leading to suboptimal bidding strategies. This issue diminishes the

effectiveness of traditional reinforcement learning in large, complex auction environments. In this work, we

propose a novel transfer learning approach to address this challenge. By training agents in smaller N auctions

and transferring their learned policies to larger N settings, we signiﬁcantly reduce the occurrence of local

equilibrium. This method not only accelerates training but also enhances convergence toward optimal Nash

equilibrium strategies in multi-agent settings. Our experimental results show that transfer learning successfully

overcomes the limitations observed in previous research, yielding more robust and efﬁcient bidding strategies

in all-pay auctions.

1 INTRODUCTION

In multi-agent all-pay auctions, agents are tasked with

bidding strategies that maximize their expected pay-

offs in a highly competitive environment.

research utilizing Multi-Agent Deep Deterministic

Policy Gradient (MADDPG) has demonstrated that

agents can converge to Nash equilibrium in smaller

auctions with fewer participants (Craizer et al., 2025).

However, as the number of agents increases, a phe-

nomenon of local equilibrium often emerges, where

certain agents bid optimally while others fall into sim-

plistic strategies, such as bidding 0.0, effectively opt-

ing out of competition. This behavior undermines the

strategic complexity of the auction and leads to sub-

optimal overall outcomes.

The difﬁculty of achieving global equilibrium in-

creases exponentially with the number of agents, as

the strategy space becomes more complex. This

presents a signiﬁcant challenge in ensuring that agents

learn optimal bidding behaviors in larger auctions,

particularly when initializing from a random state.

https://orcid.org/0009-0001-5112-2679

https://orcid.org/0000-0002-4999-7476

https://orcid.org/0000-0001-6519-1264

This section was revised for grammar and wording

with assistance from ChatGPT-3.

To address this issue, we propose leveraging transfer

learning as a means to improve training in these high-

dimensional environments. Speciﬁcally, we train

agents in lower-N auctions, where convergence to

Nash equilibrium is more feasible, and then transfer

the learned models and parameters to auctions with

a greater number of agents. While we initially at-

tempted a direct approach to larger auctions, applying

the transfer process stepwise, gradually increasing the

number of agents, proved to yield better results.

The primary contributions of this work are

twofold. First, we propose a transfer learning frame-

work designed for multi-agent all-pay auctions, which

effectively mitigates the emergence of local equi-

librium in higher-N settings. By leveraging pre-

trained models from simpler auction scenarios, we

signiﬁcantly improve the scalability of the training

process, enabling robust convergence to near-Nash

equilibrium strategies. Second, we adapt the critic

network architecture to accommodate the increased

complexity of larger agent populations, ensuring the

model’s effectiveness in higher-dimensional environ-

ments. These contributions lay the groundwork for

extending transfer learning techniques to other com-

plex auction formats and multi-agent systems, of-

fering new insights into strategic decision-making in

competitive scenarios.

534

Craizer, L. E., Hermann, E. and Silva, M. A.

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions.

DOI: 10.5220/0013294000003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 534-543

ISBN: 978-989-758-749-8; ISSN: 2184-4992

2 RELATED WORK

Deep Reinforcement Learning (DRL), an approach

that integrates deep learning with reinforcement

learning principles, enables agents to learn decision-

making strategies through cumulative reward maxi-

mization in an environment, largely without explicit

supervision (Sutton, 2018). DRL’s effectiveness has

been propelled by major contributions from OpenAI

and DeepMind, whose development of environments

like Gymnasium and pioneering models such as DQN

(Mnih et al., 2015), AlphaZero (Schrittwieser et al.,

2020), A3C (Mnih, 2016), and PPO (Schulman et al.,

2017) have signiﬁcantly advanced the ﬁeld. With the

rise of multi-agent reinforcement learning (MARL),

algorithms such as MADDPG and MAPPO have been

developed to manage the challenges of non-stationary

and partially observable environments, making these

approaches highly applicable to competitive and co-

operative multi-agent scenarios.

In auction theory, DRL has become a prominent

tool for simulating and understanding strategic be-

haviors in complex auction types. Recent studies by

Kannan (Kannan et al., 2019) and Luong et al. (Lu-

ong et al., 2018) use agent-based simulations pow-

ered by DRL to analyze human decision-making pat-

terns within auction frameworks. Gemp’s research

explores DRL application in all-pay auctions, focus-

ing on scenarios where traditional equilibrium analy-

sis is computationally infeasible (Gemp et al., 2022).

Moreover, D

utting (D

utting et al., 2021) and Feng ad-

vance auction models by employing neural networks

to bridge theoretical gaps in expected and observed

outcomes, notably in multi-item auction settings.

Relevant to our study are the contributions

by Bichler, whose Neural Pseudo-Gradient Ascent

(NPGA) algorithm offers innovative ways to estimate

equilibrium in symmetric auctions, especially within

all-pay environments (Bichler et al., 2021). Bich-

ler’s work highlights the potential for DRL algorithms

to identify and approximate equilibrium strategies in

auctions lacking explicit equilibrium formulas, under-

scoring the robustness of DRL for analyzing com-

plex auction formats (Ewert et al., 2022). Further-

more, his work provides insights into human behav-

ioral deviations from neutral to risk-averse equilib-

rium, a phenomenon our study also examines in all-

pay auctions. This cumulative body of research val-

idates DRL’s versatility and relevance, positioning it

as an essential tool for addressing increasingly intri-

cate auction dynamics.

Transfer learning (TL) in deep reinforcement

learning (DRL) has gained attention as an approach

to address some of RL’s core challenges, such as

sample inefﬁciency and the exploration-exploitation

trade-off. By enabling agents to apply previously ac-

quired knowledge to new, related tasks, TL acceler-

ates learning and improves performance in complex

environments where direct training is costly or im-

practical (Zhu et al., 2023). Traditional RL meth-

ods often rely on agents learning from scratch, a

process that can be inefﬁcient, particularly in high-

dimensional tasks where tabula rasa learning can be

prohibitive (Taylor and Stone, 2009). By leverag-

ing knowledge from earlier tasks, TL enables gen-

eralization across tasks rather than just within a sin-

gle task, a concept rooted in psychology and cogni-

tive science (Lazaric, 2012). In DRL, various transfer

methods, such as policy distillation and representation

disentanglement, have demonstrated success in apply-

ing generalizable strategies to complex domains like

robotics and autonomous systems, highlighting TL’s

potential to enhance RL performance across diverse

applications.

3 BACKGROUND

Auctions are highly popular mechanisms for allocat-

ing goods and services to economic agents.

There

is a wide variety of auction designs concerning par-

ticipation rules, types of items being auctioned, bid-

ding rules for participants, allocation of goods based

on bids, and payment regulations.

Despite the wide variety of auctions, it is sufﬁcient

for the purposes of this work to focus on the simple

case of auctions with private and independent values.

In these auctions, each participant assigns a unique

value to the item. An art auction serves as a good

example. One participant might ﬁnd the painting be-

ing auctioned beautiful and therefore highly valuable,

while another might consider it unattractive and as-

sign it a low value. Additionally, we will consider

ﬁrst-price sealed-bid auctions. In these auctions, par-

ticipants submit their bids without knowing the bids

of others. The participant who submits the highest

bid wins the item being auctioned.

Auction theory is a branch of game theory, as each

participant’s payoff depends on their own action (bid)

as well as the actions of others. Participants aim to

maximize their payoff. Auction theory boasts a vast

literature, where optimal strategies or Nash equilib-

rium for various types of auctions are studied. The

strategies are described in terms of the ”bid function”

b(v), where the bid is a function of the value assigned

to the auctioned item. In the following section, we

This section was revised for grammar and wording

with assistance from ChatGPT-3.

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions

535

present some theoretical results for the auction de-

signs chosen for the experiments in this work. The

results can be found in (Klemperer, 1999), (Krishna,

2009) or (Menezes and Monteiro, 2008).

3.1 Algorithm Design

This research examines sealed-bid auctions involving

a single item. Here, the auctioneer determines the

winning bid from N participating agents. We conduct

n auction rounds to observe the agents’ behaviour and

learning patterns, seeking convergence in their bids

for each given value or signal over time. Each player

i has a value v

for the item. In private value auctions

these values may differ among participants. The proﬁt

function for each agent is deﬁned based on their bids:

: R → R, where B is the vector space of possible

bids of all agents. For example, in a sealed ﬁrst-price

auction of private values, a (risk-neutral) participant

i’s proﬁt function is:

, b

) =



− b

if b

> max(b

)

0 otherwise

(1)

where b

represents the bids of other participants, ex-

cluding b

3.2 The Rational Bid

Each participant i receives a value v

, representing the

value that she privatelly attributes for the item. Based

on this value v

, participant i formulates a bid b

The expected payoff for participant i is given by:

E[u

] =

u(π(b

), y)) f

(y)dy

Here, f

(y) is the probability density function of

the vector y, which contains the bids of other partic-

ipants. Participants aim to maximize their expected

reward, which requires knowledge of the function

(y), dependent on other players’ policies.

3.3 Types of Auctions

3.3.1 First Price Auction

The ﬁrst-price auction is the most well-known auc-

tion design. The allocation rule is straightforward: the

item is awarded to the participant with the highest bid

(ignoring any tie-breaking rules for simplicity). The

payment rule is also simple: the winning participant

pays the amount they bid, while the non-winning bid-

ders do not pay anything. Therefore, the payoff of a

participant i is

(

− b

if b

> max

j̸=i

)

0 otherwise

(2)

where v

is player i’s valuation, b

is their bid, and b

are the bids of other players. The Nash equilibrium of

this auction when the private values come from uni-

form [0,1] independent distributions and the partici-

pants are risk-neutral is the same bid function for all

(Krishna, 2009)

∗

(N − 1)v

3.3.2 Second Price Auction

The allocation rule of the second-price auction (also

known as a Vickrey auction, after the seminal work of

Vickrey [1961]) is the same as that of the ﬁrst-price

auction: the winner is the participant with the highest

bid. However, the payment rule differs: the winner

pays the amount of the second-highest bid, not their

own bid. The interest in this type of auction stems

from the fact that the Nash equilibrium strategy for

each participant is to bid their true valuation of the

item, i.e., the bid function is the identity (Krishna,

2009):

3.3.3 All-Pay Auction

In an all-pay auction, the allocation rule is the same

as previously described: the item is awarded to the

participant with the highest bid. The unique aspect of

this auction lies in its payment rule: all participants

must pay their bids, regardless of whether they win.

In this scenario, the Nash equilibrium for risk-neutral

participants is determined by the bid function

∗

(N − 1)

4 METHODOLOGY

4.1 Agents Training and Evaluation

In this study, we employ the Multi-Agent Deep De-

terministic Policy Gradient (MADDPG) algorithm to

train agents in auction environments, speciﬁcally fo-

cusing on optimizing bidding strategies.

Each agent

is equipped with its own actor and critic networks,

where the critic is trained using the observations and

actions of all agents, capturing the interdependent na-

ture of multi-agent environments like auctions. The

This section was revised for grammar and wording

with assistance from ChatGPT-3.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

536

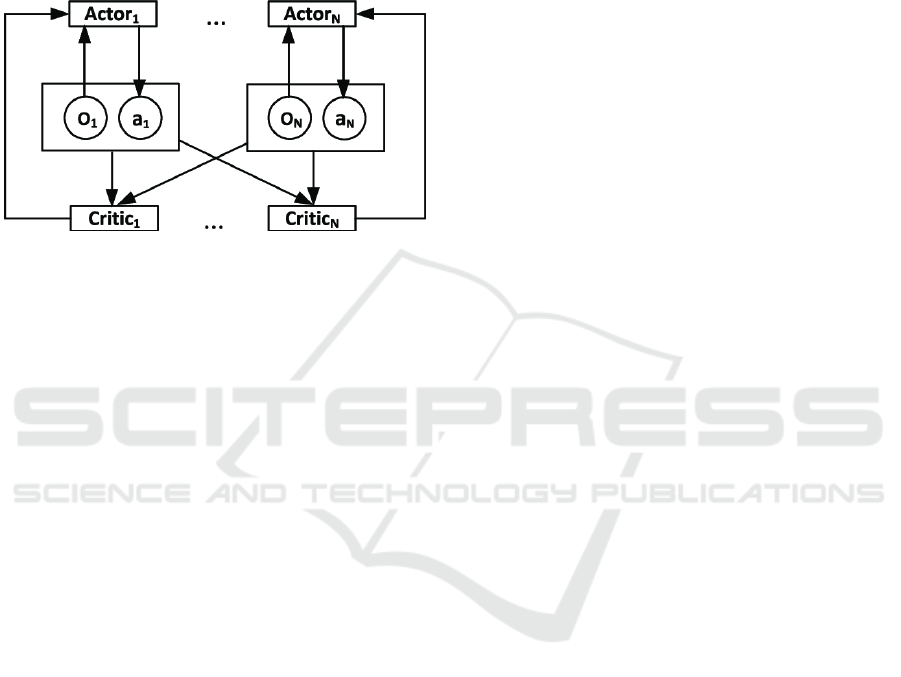
training process involves iterative learning, where

agents receive private values at the beginning of each

auction round and choose actions (bids) to maximize

their expected utility based on rewards determined by

the auction’s payment rules. This setup allows agents

to reﬁne their strategies over time. The MADDPG

architecture and workﬂow used in our approach is il-

lustrated in Figure 1.

Figure 1: MADDPG Architecture - Figure taken from

(Zheng and Liu, 2019).

To stabilize the learning process, we implement a

Replay Buffer, which stores past experiences to break

the correlation between consecutive interactions, al-

lowing the agents to learn more effectively from a di-

verse set of experiences. We experiment with various

buffer conﬁgurations, including a Combined Experi-

ence Replay Buffer (Zhang and Sutton, 2017), which

merges historical experiences with the most recent

interactions. This approach is particularly useful in

dynamic environments, where the agent’s policy is

continually evolving. Additionally, we introduce dy-

namic noise in the agents’ actions to balance explo-

ration and exploitation. Early in training, higher noise

encourages exploration of different bidding strategies,

while later stages reduce the noise to focus on exploit-

ing optimal strategies.

The neural network architecture consists of both

actor and critic networks, each containing two layers

with 100 neurons. The output layer uses a sigmoid

activation function. During training, a batch size of

64 is used, with an actor learning rate set to 0.000025

and a critic learning rate of 0.00025. To aid the learn-

ing process, a decay factor is also applied. All hy-

perparameters, including the number of neurons per

layer, were chosen based on preliminary experiments

to ensure a balance between model performance and

computational efﬁciency.

4.2 Transfer Learning in Auctions

In auction scenarios, particularly in multi-agent set-

tings like all-pay auctions, ﬁnding a good starting

point for training can signiﬁcantly improve the efﬁ-

ciency and success of the learning process. In our

previous research, we observed that as the number of

agents N increased, agents often converged to a lo-

cal equilibrium, where some of them would bid 0.0

for any private value, thus underperforming. This is-

sue became especially prominent when N ≥ 3, as ran-

dom initialization did not provide sufﬁcient guidance

for the agents to explore more effective strategies. In

this work, we propose the use of transfer learning

to overcome this challenge by using trained models

from lower-N auctions as a starting point for training

agents in higher-N auctions. This allows us to provide

agents with better initial conditions, reducing the risk

of falling into suboptimal equilibrium.

Transfer learning in this context involves training

agents in a smaller game space, with fewer players,

where they can more easily learn stable strategies.

Once these agents have been trained in a lower-N auc-

tion scenario, such as N = 2, we replicate their mod-

els for use in higher-N auctions. For instance, if we

transition from N = 2 to N = 5, we can choose one

or both of the initial agents, duplicate their parame-

ters, and use them to populate the additional agents

in the new setting. By starting with agents who have

already converged to near-optimal policies, we can re-

duce the need for extensive retraining, and more im-

portantly, avoid the instability that arises when start-

ing from random initialization. This technique sig-

niﬁcantly accelerates convergence and leads to more

efﬁcient training.

The beauty of this approach lies in the ﬂexibil-

ity of how these agents are duplicated and retrained.

Since agents in lower-N scenarios often converge to

very similar policies, there is little difference in which

agents are duplicated for higher-N games. We can use

any combination of the original agents’ parameters to

initialize the new ones. After duplication, the agents

are then retrained to account for the new competitive

environment with more participants. This method not

only speeds up the learning process but also helps to

address issues seen in previous work, such as local

equilibrium that result from poorly initialized param-

eters.

A key technical challenge arises when increas-

ing the number of agents: the input structure of the

critic network must be adjusted. In multi-agent re-

inforcement learning, the critic takes into account

the states and actions of all agents to evaluate each

agent’s decision-making process. When we scale

from a lower-N to a higher-N auction, the input size

of the critic increases accordingly, leading to dimen-

sion mismatches. Initially, this posed a programming

error, as the critic’s input was built for a smaller input

space. This mismatch had to be addressed to ensure

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions

537

seamless scaling of the model.

To resolve this, we exploited the deep neural net-

works’ capacity for handling redundancy in inputs.

For the critic network, we duplicated the states and

actions of the original agents as needed to match the

higher N. By duplicating these inputs, we ensured the

critic could still evaluate the joint actions of all agents,

even if the inputs were redundant. Furthermore, to

prevent future programming errors when scaling the

model, we modiﬁed the critic’s architecture during the

training of the initial agents. We added extra input

slots to accommodate additional agents, ensuring that

when scaling up, the critic would already be prepared

for the increased input size. This adaptation allowed

us to maintain the critic’s function without compro-

mising the model’s performance, providing a stable

and scalable approach for transfer learning in auction

settings.

However, this one-step transfer learning approach

does not always yield optimal results or achieve near

Nash equilibrium, especially as the number of agents

increases. To address this, we introduced a more ro-

bust step-by-step heuristic for scaling up the number

of agents while maintaining stability. Starting with

trained agents from an N = 2 auction, we incremen-

tally introduced one new agent at a time, progres-

sively moving to N = 3, N = 4, and so on. At each

step, the new agent’s initial parameters were taken

from one of the existing agents, ensuring a consis-

tent starting point, while the entire ensemble was re-

trained to adapt to the new environment. This gradual

increase allowed the agents to adjust more seamlessly

to the added complexity, facilitating smoother conver-

gence.

This iterative method proved particularly effective

in preventing agents from defaulting to suboptimal

behaviors, such as bidding 0.0 for all private values.

The step-by-step integration helped the network man-

age increased strategic interactions without destabi-

lizing the learning process. By methodically expand-

ing the training environment, agents had the opportu-

nity to adapt incrementally, resulting in more robust

policy learning and a higher likelihood of achieving a

global Nash equilibrium, as described in Section 5.

5 RESULTS

This section presents the experimental results, start-

ing with basic auction types—ﬁrst-price and second-

price auctions—to validate the efﬁcacy of the multi-

agent deep reinforcement learning (DRL) approach

in relatively straightforward settings.

In these stan-

dard auctions, transfer learning was not required for

the DRL agents to reach equilibrium strategies. The

agents naturally converged toward near-Nash equilib-

rium without getting stuck in local solutions, which

often occurs in more complex auction types. This lack

of dependence on transfer learning in basic auctions

highlights the algorithm’s ability to learn optimal bid-

ding behavior when the strategic landscape presents

fewer challenges.

Figures 2 (ﬁrst-price auction with N = 3 and N =

5) and 3 (second-price auction with N = 3 and N = 6)

illustrate the agents’ steady convergence to expected

equilibrium behaviors. These results align closely

with theoretical predictions, conﬁrming the robust-

ness of the DRL model in simpler auction environ-

ments and demonstrating that agents can efﬁciently

learn and adapt without needing additional techniques

such as transfer learning. This strong foundational

performance in standard auctions sets the stage for

examining the more complex dynamics of all-pay

auctions, where the beneﬁts of transfer learning be-

come essential for overcoming challenges such as lo-

cal equilibrium.

In more complex settings, such as the all-pay auc-

tion, transfer learning proved valuable for enabling

DRL agents to reach equilibrium despite the added

strategic complexity. Instead of directly transition-

ing from a smaller-scale N = 2 auction to a larger

N = 5 auction, we employed a step-by-step transfer

learning approach. The model was ﬁrst trained with

two agents, which successfully converged to a near-

Nash equilibrium. This learned strategy was then in-

crementally scaled by introducing one new agent at

a time and retraining the ensemble at each step (e.g.,

N = 2 → N = 3 → N = 4 → N = 5). This gradual ap-

proach allowed agents to adapt incrementally to the

increasing strategic complexity, mitigating the risk of

falling into suboptimal local equilibrium. The pro-

gression of this approach is illustrated in Figure 4,

where the left subﬁgure (4a) shows the two-agent

equilibrium and the other players bidding zero for any

private value, while the right subﬁgure (4b) displays

the successful equilibrium achieved in the four-agent

setup. This example demonstrates how transfer learn-

ing allows learned strategies to scale effectively, en-

abling agents to adapt efﬁciently even in increasingly

complex environments.

As the auction size increased further, the strategic

complexity grew, and new challenges became evident.

In the all-pay structure, each participant must pay

their bid regardless of winning, which creates a strate-

This section was revised for grammar and wording

with assistance from ChatGPT-3.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

538

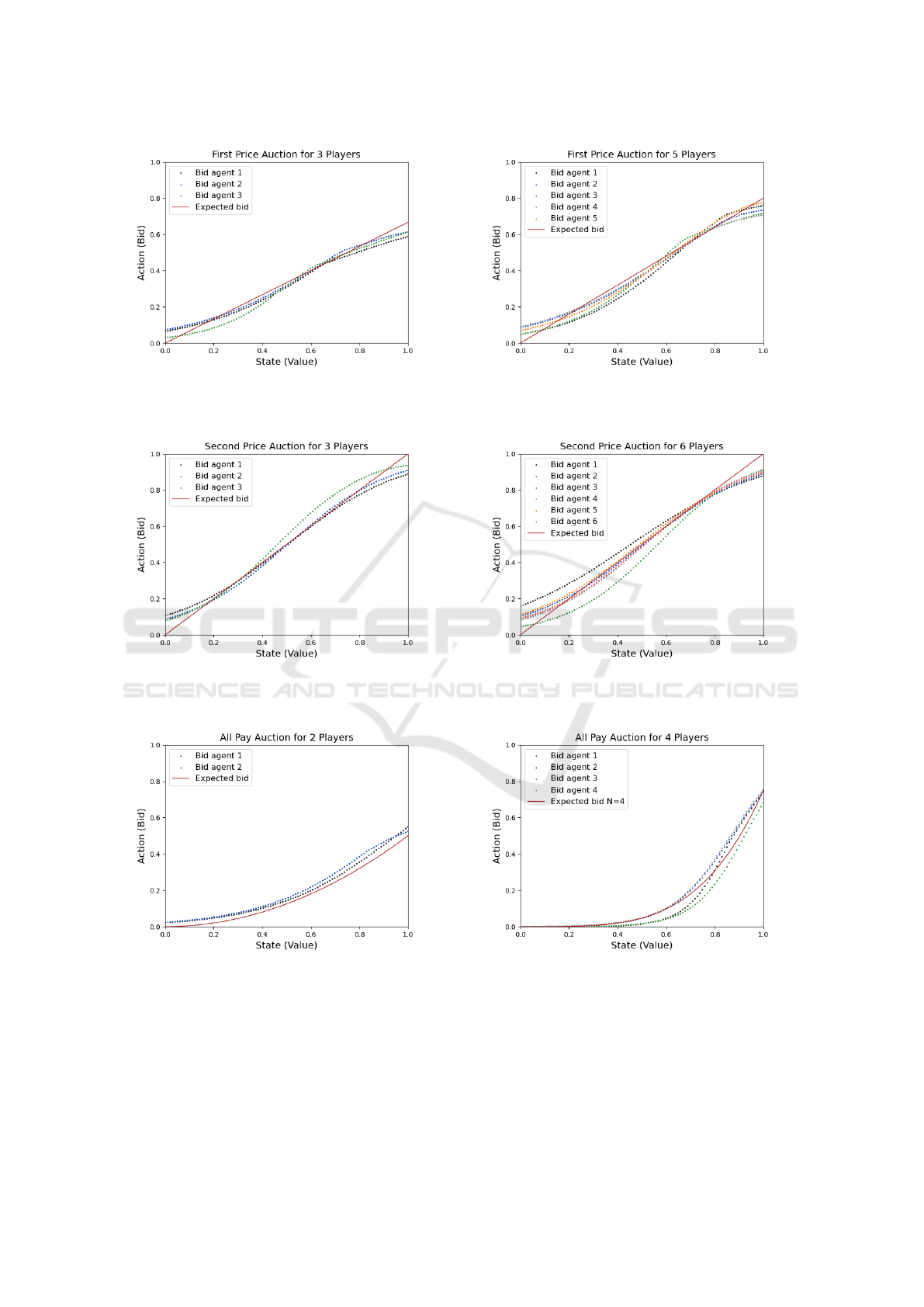
(a) First Price with 3 agents. (b) First Price with 5 agents.

Figure 2: First Price Auction Results.

(a) Second Price with 3 agents. (b) Second Price with 6 agents.

Figure 3: Second Price Auction Results.

(a) All Pay with 2 agents. (b) All Pay with 4 agents starting from 2 agents.

Figure 4: Transfer Learning in All-Pay Auctions: convergence from N = 2 to N = 4 Agents.

gic landscape where suboptimal behaviors, such as

zero-bidding, are more likely as the number of agents

increases. This growth in complexity often led agents

to fall into local minimum, deviating from Nash equi-

librium strategies. Without additional support, such

as transfer learning, agents in larger-scale settings

struggled to maintain optimal policies, highlighting

the limitations of reinforcement learning alone in han-

dling the increasing strategic demands.

Transfer learning addressed these challenges by

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions

539

initializing agents with pre-trained policies from sim-

pler, smaller-scale auctions. This approach allowed

agents to begin from a more informed position rather

than random initialization, helping them avoid com-

mon pitfalls. As shown in Figures 5, 6, and 7,

agents that beneﬁted from transfer learning not only

avoided local equilibrium but also exhibited compet-

itive strategies, with all agents converging to near-

equilibrium behavior. The improvement in conver-

gence was particularly pronounced in the N = 5 auc-

tion.

While due to the inherent stochasticity of these

algorithms, convergence is not always guaranteed,

transfer learning signiﬁcantly improves convergence

rates and helps agents avoid suboptimal bidding

strategies. As the number of participants (N) in-

creases, the likelihood of some agents getting stuck in

local minimum also grows, reﬂecting the heightened

strategic complexity in larger settings. Despite this,

the transfer learning approach consistently outper-

forms random initialization, enabling more agents to

converge to near-equilibrium strategies even in chal-

lenging scenarios.

In summary, transfer learning has proven to be a

highly effective technique for addressing key chal-

lenges in multi-agent DRL for all-pay auctions. By

initializing agents with strategies learned in smaller-

scale auctions, we facilitated more efﬁcient learning

and achieved stable convergence across increasingly

complex environments. The approach demonstrated

strong results, particularly in settings with participant

numbers ranging from N = 2 to N = 6, showing its

robustness in navigating the strategic complexity of

all-pay auctions. While some limitations remain, par-

ticularly in scenarios with larger participant numbers

where convergence can still be challenging, the over-

all performance underscores the potential of transfer

learning as a powerful strategy for enhancing learn-

ing efﬁciency and equilibrium convergence in com-

petitive multi-agent systems.

6 DISCUSSION

The aim of this study was to introduce and evalu-

ate a novel approach to training agents in multi-agent

auction environments using transfer learning tech-

niques.

Speciﬁcally, we focused on improving the

convergence of deep reinforcement learning (DRL)

agents in all-pay auctions, where previous research

encountered challenges in ﬁnding equilibrium strate-

gies as the number of participants (N) increased. Our

This section was revised for grammar and wording

with assistance from ChatGPT-3.

transfer learning method proved highly effective in

addressing these issues by using pre-trained agents

from smaller auctions and using them as a starting

point for training agents in more complex, higher-N

auction scenarios.

Our results demonstrate that this approach offers

signiﬁcant advantages over traditional random ini-

tialization methods, particularly in complex auction

types like all-pay auctions, where convergence to a

Nash equilibrium is notoriously difﬁcult. By employ-

ing a stepwise transfer learning approach, where mod-

els were incrementally trained starting from lower-N

auctions and moving to higher-N scenarios, agents

began the training process with a strong initial con-

dition. This method enabled them to avoid sub-

optimal bidding strategies, such as consistently bid-

ding zero, which were prevalent in previous studies.

The stepwise strategy effectively mitigated the occur-

rence of local equilibrium, where agents placed zero

bids regardless of their private values, a problem that

plagued our earlier research.

The novelty of this approach lies in its ability to

solve the critical issue of local equilibrium by ini-

tializing agents with parameters that are more aligned

with optimal strategies. By reusing agents trained in

auctions with fewer participants, we provided them

with a near-optimal bidding strategy that could be

adapted to higher-N environments. This not only im-

proved the efﬁciency of the training process, but also

increased the agents’ ability to learn robust bidding

strategies in larger and more complex auctions. Ad-

ditionally, we adapted the critic network to account

for the changing number of participants in higher-N

auctions. This modiﬁcation involved designing the

critic network to accommodate additional agent in-

puts by duplicating existing inputs, allowing the net-

work to effectively process the higher-dimensional in-

put space without requiring a complete reinitialization

of network parameters.

However, as N becomes larger, the algorithm faces

increasing challenges in maintaining performance and

achieving convergence. The added complexity of in-

teractions among a higher number of agents creates

a larger strategy space, making it more difﬁcult for

agents to reach an optimal equilibrium. In particular,

the probability of local minimum increases as agents

struggle to adapt to the expanding competitive envi-

ronment. Although transfer learning signiﬁcantly im-

proves scalability, the diminishing returns observed

for very large N highlight the need for further reﬁne-

ments, such as adaptive learning mechanisms or more

sophisticated initialization strategies.

In summary, the transfer learning approach we im-

plemented in this study represents a substantial im-

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

540

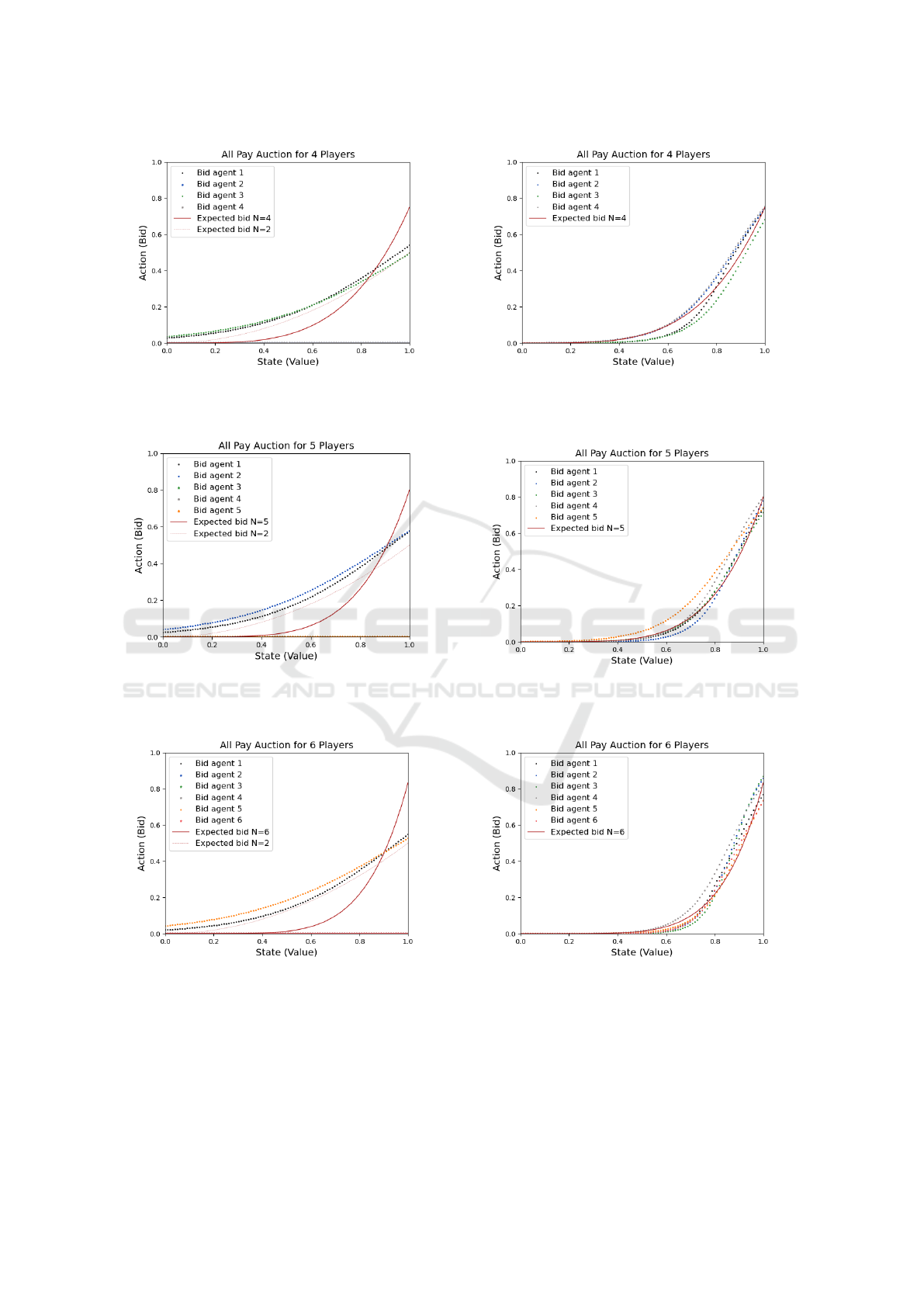
(a) All Pay with 4 agents - Regular Learning. (b) All Pay Auction with 4 agents - Transfer Learning.

Figure 5: All Pay with 4 agents.

(a) All Pay with 5 agents - Regular Learning. (b) All Pay with 5 agents - Transfer Learning.

Figure 6: All Pay Auction with 5 agents.

(a) All Pay with 6 agents - Regular Learning. (b) All Pay with 6 agents - Transfer Learning.

Figure 7: All Pay Auction with 6 agents.

provement in training DRL agents in all-pay auctions

and similar multi-agent settings. By leveraging pre-

trained models, we not only solved critical issues

from previous research but also laid the groundwork

for further applications of transfer learning in other

complex auction formats. This method holds promise

for improving learning efﬁciency in a variety of auc-

tion types and multi-agent systems, ultimately broad-

ening the applicability of DRL in strategic decision-

making environments.

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions

541

7 CONCLUSIONS

This study introduced a novel transfer learning ap-

proach for training agents in multi-agent auction

environments, speciﬁcally focusing on all-pay auc-

tions.

The results demonstrated strong performance

in enabling agents to converge toward Nash equilib-

rium strategies by leveraging pre-trained models from

smaller auctions. This method effectively mitigated

challenges associated with local equilibrium and sig-

niﬁcantly enhanced the efﬁciency of the learning pro-

cess.

Our ﬁndings indicate that transfer learning is par-

ticularly effective even when there is a substantial

difference in the number of agents between the pre-

trained and new models, especially when using a step-

by-step transfer approach. By incrementally introduc-

ing one agent at a time, we observed enhanced perfor-

mance and scalability, allowing for better adaptation

to larger agent populations. Again, as N increases, the

growing strategy space and heightened risk of conver-

gence to local minimum pose challenges, emphasiz-

ing the need for enhanced techniques to ensure efﬁ-

ciency in high-N environments.

Future work will explore scaling the algorithm to

handle auctions with signiﬁcantly larger N, as well as

extending its application to auctions with interdepen-

dent values. In interdependent value settings, the val-

uation of the item depends not only on private signals

but also on shared external factors, creating additional

complexity in learning optimal strategies. Investigat-

ing how transfer learning performs in these environ-

ments will provide valuable insights into its adaptabil-

ity and robustness. Additionally, comparative experi-

ments with other transfer learning methods and alter-

native DRL architectures are planned to evaluate the

effectiveness of the proposed approach against state-

of-the-art techniques. Furthermore, we aim to reﬁne

the proposed method by incorporating adaptive learn-

ing rates, exploring curriculum learning, and testing it

in broader multi-agent environments. These enhance-

ments will help generalize the approach to a wider

range of auction formats, ultimately contributing to

more effective strategic decision-making in competi-

tive and cooperative systems.

The incremental approach used in this study

aimed to mitigate the emergence of local equilib-

rium by starting from a simpler problem and grad-

ually transforming it into the target problem. This

technique is inspired by methods like numerical con-

tinuation (Allgower and Georg, 2012), where a prob-

lem is solved incrementally by starting with a simpler,

This section was revised for grammar and wording

with assistance from ChatGPT-3.

well-understood version and progressively increasing

its complexity. In our case, agents trained in lower-N

auctions adapted their strategies step by step as new

agents were introduced, avoiding the abrupt strategy

shifts often associated with random initialization in

higher-N settings. While this approach proved effec-

tive for the scenarios tested, we recognize that the efﬁ-

ciency and success of this method may depend on the

speciﬁc auction format and the way the incremental

transition is implemented.

Moreover, we envision applying this technique to

broader DRL applications, particularly in scenarios

where agents often achieve suboptimal strategies and

lack incentives to leave such states, exempliﬁed by

local equilibrium. In general, the promising results

of our experiments suggest that transfer learning can

play a crucial role in enhancing the training of agents

in complex auction scenarios. By building on the

foundation established in this study, we aim to fur-

ther investigate the application of this approach across

a broader range of auction types and multi-agent en-

vironments, ultimately contributing to more effective

strategic decision-making in competitive settings.

REFERENCES

Allgower, E. L. and Georg, K. (2012). Numerical continu-

ation methods: an introduction, volume 13. Springer

Science & Business Media.

Bichler, M., Fichtl, M., Heidekr

uger, S., Kohring, N., and

Sutterer, P. (2021). Learning equilibria in symmetric

auction games using artiﬁcial neural networks. Nature

machine intelligence, 3(8):687–695.

Craizer, L. E., Hermann, E., and Alvim, M. (2025). Learn-

ing optimal bidding strategies in all-pay auctions. In

Proceedings of the International Conference on Arti-

ﬁcial Intelligence and Soft Computing (ICAISC), vol-

ume 15165 of Lecture Notes in Computer Science.

Springer. To appear.

utting, P., Feng, Z., Narasimhan, H., Parkes, D. C.,

and Ravindranath, S. S. (2021). Optimal auctions

through deep learning. Communications of the ACM,

64(8):109–116.

Ewert, M., Heidekr

uger, S., and Bichler, M. (2022). Ap-

proaching the overbidding puzzle in all-pay auctions:

Explaining human behavior through bayesian opti-

mization and equilibrium learning. In Proceedings

of the 21st International Conference on Autonomous

Agents and Multiagent Systems, pages 1586–1588.

Gemp, I., Anthony, T., Kramar, J., Eccles, T., Tacchetti, A.,

and Bachrach, Y. (2022). Designing all-pay auctions

using deep learning and multi-agent simulation. Sci-

entiﬁc Reports, 12(1):16937.

Kannan, K. N., Pamuru, V., and Rosokha, Y. (2019). Us-

ing machine learning for modeling human behavior

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

542

and analyzing friction in generalized second price auc-

tions. Available at SSRN 3315772.

Klemperer, P. (1999). Auction theory: A guide to the liter-

ature. Journal of economic surveys, 13(3):227–286.

Krishna, V. (2009). Auction theory. Academic press.

Lazaric, A. (2012). Transfer in reinforcement learning: a

framework and a survey. In Reinforcement Learning:

State-of-the-Art, pages 143–173. Springer.

Luong, N. C., Xiong, Z., Wang, P., and Niyato, D. (2018).

Optimal auction for edge computing resource man-

agement in mobile blockchain networks: A deep

learning approach. In 2018 IEEE international con-

ference on communications (ICC), pages 1–6. IEEE.

Menezes, F. and Monteiro, P. (2008). An introduction to

auction theory: Oxford university press.

Mnih, V. (2016). Asynchronous methods for deep rein-

forcement learning. arXiv preprint arXiv:1602.01783.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-

ness, J., Bellemare, M. G., Graves, A., Riedmiller, M.,

Fidjeland, A. K., Ostrovski, G., et al. (2015). Human-

level control through deep reinforcement learning. na-

ture, 518(7540):529–533.

Schrittwieser, J., Antonoglou, I., Hubert, T., Simonyan, K.,

Sifre, L., Schmitt, S., Guez, A., Lockhart, E., Hass-

abis, D., Graepel, T., et al. (2020). Mastering atari,

go, chess and shogi by planning with a learned model.

Nature, 588(7839):604–609.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

Sutton, R. S. (2018). Reinforcement learning: An introduc-

tion. A Bradford Book.

Taylor, M. E. and Stone, P. (2009). Transfer learning for

reinforcement learning domains: A survey. Journal of

Machine Learning Research, 10(7).

Zhang, S. and Sutton, R. S. (2017). A deeper look at expe-

rience replay. arXiv preprint arXiv:1712.01275.

Zheng, S. and Liu, H. (2019). Improved multi-agent deep

deterministic policy gradient for path planning-based

crowd simulation. Ieee Access, 7:147755–147770.

Zhu, Z., Lin, K., Jain, A. K., and Zhou, J. (2023). Trans-

fer learning in deep reinforcement learning: A survey.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 45(11):13344–13362.

Leveraging Transfer Learning to Improve Convergence in All-Pay Auctions

543