Time-Aware Contrastive Representation Learning for Road Network and
Trajectory
Ashraful Islam Shanto Sikder and Naushin Nower
Institute of Information Technology, University of Dhaka, Dhaka, Bangladesh
Keywords:
Contrastive Learning, Mutual Information, Transformer, Hard Negative Sampling.
Abstract:
Modeling and learning representations for road networks and vehicle trajectories is essential for improving
various Intelligent Transportation System (ITS) applications. Existing methods often treat road network and
trajectory data separately, focus only on one, employ two-step processes that result in information loss and
error propagation, or ignore temporal dynamics. To address these limitations, we propose a framework called
Time-Aware Contrastive Representation Learning for Road Network and Trajectory (TCRLRT). Our approach
introduces an end-to-end model that simultaneously learns road network and trajectory representations, en-
hanced by a temporal encoding module that captures temporal information and a synthesized hard negative
sampling module to enhance the discriminative power of the learned representations. We validate the ef-
fectiveness of TCRLRT through extensive experiments conducted on two real-world datasets, demonstrating
improved performance over baseline methods across multiple downstream tasks. The results highlight the
advantages of joint representation learning with temporal modeling and hard negative sampling, leading to
robust and versatile representations.
1 INTRODUCTION
Vehicle technology and intelligent transportation sys-
tems (ITS) (Yangxin Lin and Ma, 2017) are key to
enhancing safety, efficiency, and sustainability. A
fundamental challenge within ITS is to accurately
model and understand the interactions between road
networks and vehicle trajectories. Effective represen-
tation learning (Yoshua Bengio and Vincent, 2013)
for road networks and trajectories transforms complex
spatial-temporal data into machine-interpretable for-
mats, facilitating various applications such as travel
time estimation, traffic speed inference, route predic-
tion, etc.
A road network can be described as a type of
graph structure that represents the interconnected lay-
out of road segments, encompassing both the topolog-
ical structure and additional contextual details about
the connections between these segments. On the other
hand, a trajectory represents sequential data com-
posed of successive road segments that capture spa-
tial and temporal movement patterns, embedding the
dynamic nature of mobility and the associated seman-
tics. The structural and temporal characteristics of
road networks and vehicle movements can be cap-
tured through representation learning methods, and
the learned representations can be directly used in a
variety of downstream tasks by fine-tuning.
Most existing representation learning models ei-
ther focus solely on road networks or trajectory
data (Tobias Skovgaard Jepsen and Nielsen, 2019;
Ning Wu and Pan, 2020; Meng-xiang Wang and
Yu, 2019). Treating them separately leads to ig-
noring the valuable inter-relations between them. l
Recent approaches have demonstrated that integrat-
ing road network representations into trajectory learn-
ing, or vice-versa leads to more robust representations
(Peng Han and Zhang, 2021; Yile Chen and Ellison,
2021; Yu Zheng and Ma, 2009). Existing methods of-
ten adopt a two-stage approach, where they first learn
the representation of one aspect and then use it as a
foundation for the other. However, this type of ap-
proach leaves room for error propagation between the
stages and can not directly define the objectives to
learn the cross-scale relationship between road net-
work and trajectory.
Contrastive learning (Ting Chen and Hinton,
2020) has recently emerged as a promising technique
in semi-supervised settings, leveraging cross-scale in-
formation to learn the inter-related representations
effectively, by maximizing their mutual information
(Philip Bachman and Buchwalter, 2019). JCLRNT
498
Sikder, A. I. S. and Nower, N.
Time-Aware Contrastive Representation Learning for Road Network and Trajectory.
DOI: 10.5220/0013297700003941
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 498-505
ISBN: 978-989-758-745-0; ISSN: 2184-495X
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

(a) Two different trajectories. (b) Extracted road network.
Figure 1: Two different trajectories with the same source
and destination (a) and the underlying road network (b) in
Xian.
(Zhenyu Mao and Zhao, 2022) introduced a jointly
contrastive learning framework that learns road net-
work and trajectory representations simultaneously.
However, they overlooked temporal dynamics, which
are crucial for representation learning.
To address the limitations, we propose Time-
Aware Road Network and Trajectory Contrastive
Representation Learning (TCRLRT). Our model is
an end-to-end approach that jointly learns representa-
tions of road networks and trajectories while incorpo-
rating temporal information through a learnable tem-
poral encoding module. This enables the model to
capture not only the spatial structure but also the time-
sensitive nature of vehicle movements. Additionally,
we enhance the training process through the synthe-
sis of hard negative examples (Joshua Robinson and
Jegelka, 2020), which helps the model learn more dis-
criminative representations and improves its overall
performance.
In summary, our key contributions include:
1. An integrated model that jointly learns road and
trajectory representations, enriched with temporal
information to capture dynamic traffic behavior.
2. Incorporating a hard negative sampling strategy to
optimize the training process and enhance model
robustness.
3. Comprehensive experimental validation on real-
world datasets across multiple downstream tasks
demonstrates the effectiveness and versatility of
the proposed approach.
2 RELATED WORKS
Representation learning in road networks and tra-
jectories has attracted substantial attention in recent
years due to its importance in various traffic-related
applications. Existing research can be broadly cate-
gorized into road network representation learning, tra-
jectory representation learning, and joint approaches
that integrate both types of data.
The study of road network representation learn-
ing typically aims to capture road segments’ struc-
tural and functional properties. Traditional graph
embedding methods, such as Node2Vec (Grover and
Leskovec, 2016), employ biased random walks and
skip-gram models to learn node embeddings, mak-
ing them general-purpose but often insufficient for
road-specific tasks. Similarly, DGI (Deep Graph Info-
max) (Velickovic et al., 2019) leverages unsupervised
learning to maximize mutual information between lo-
cal and global graph representations but lacks explicit
traffic and road-specific adaptations. More special-
ized methods have been developed to address these
limitations. For example, RFN (Relational Fusion
Networks) (Tobias Skovgaard Jepsen and Nielsen,
2019) introduces a more targeted approach, model-
ing interactions among nodes and edges through rela-
tional views and message passing. IRN2Vec (Meng-
xiang Wang and Yu, 2019) focuses on capturing the
relationships between road segment pairs using sam-
ples from the shortest paths, enhancing the embed-
ding process by incorporating task-related informa-
tion through multi-objective learning. HRNR (Hi-
erarchical Road Network Representation) (Ning Wu
and Pan, 2020) advances these efforts by employing a
hierarchical GNN (Scarselli et al., 2009) architecture
to embed functional and structural properties at mul-
tiple levels—from road segments to larger structural
regions. Despite these advancements, many of these
methods either neglect trajectory data or only utilize
it in isolated post-processing steps, missing out on
potentially mutually beneficial learning between road
segments and traffic movement
Trajectory representation learning methods pri-
marily focus on modeling sequential movement data
for downstream tasks such as travel time prediction
and similar trajectory search. T2Vec (Xiucheng Li
and Wei, 2018) takes an approach employing an
encoder-decoder structure with LSTM (Hochreiter
and Schmidhuber, 1997) units to handle noisy tra-
jectory sequences and reconstruct trajectories to en-
hance representation learning. Advanced methods
such as Toast (Yile Chen and Ellison, 2021) go fur-
ther by integrating road network context with trajec-
tory data, applying a Transformer-based module to
incorporate auxiliary traffic information. This multi-
step approach has demonstrated success in improv-
ing trajectory-based task performance. Similarly,
GTS (Graph Trajectory Similarity) (Peng Han and
Zhang, 2021) combines POI embeddings and GNN-
LSTM networks to represent trajectories by learn-
Time-Aware Contrastive Representation Learning for Road Network and Trajectory
499

ing both point-wise and sequence-level dependencies.
Although these approaches address trajectory repre-
sentation to varying degrees, they often do so with-
out a unified approach that fully integrates road net-
work data, which can lead to suboptimal performance
in downstream applications.
Recently there have been efforts to create inte-
grated models that leverage both road and trajec-
tory data to embed interconnected elements simul-
taneously. Joint Contrastive Learning of Road Net-
work and Trajectories (JCLRNT) (Zhenyu Mao and
Zhao, 2022) presents a significant step forward by
employing a contrastive learning framework to maxi-
mize mutual information between road and trajectory
representations. However, it ignores modeling the
temporal information in the learning phase. START
(Jiawei Jiang and Wang, 2023) also proposes a frame-
work for utilizing the road network and trajectories
simultaneously, including temporal embeddings with
minutes index and day-of-week index. However, it
focuses only on trajectory representation learning.
Our proposed model builds on these existing ap-
proaches by addressing their limitations and further
enhancing the learning process. Specifically, we
model an end-to-end contrastive learning framework
with within-scale and cross-scale mutual informa-
tion maximization, incorporating temporal informa-
tion through a separate temporal encoder. The tempo-
ral information is modeled as a time-ordered sequence
in replacement of the ordinary positional encoding.
We also provide the model with synthesized harder
negative samples. This allows for a more comprehen-
sive and robust representation, leading to improved
performance across various road and trajectory-based
tasks compared to the baseline methods.
3 PRELIMINARIES
In this section, we introduce the notation and prelim-
inaries, followed by the formal problem definition.
Scalars are represented in italics (e.g., n), vectors in
lowercase boldface (e.g., h), matrices in uppercase
boldface (e.g., A), and sets in script capitals (e.g., G).
3.1 Notations and Definitions
Road Network: A road network is modeled as a di-
rected graph G = ⟨S,A
s
⟩, where S is the set of vertices
representing road segments, with |S| as the number of
segments. The adjacency matrix A
s
∈ R
|S|×|S|
has en-
tries A
s
[s
i
,s
j
] that are binary, indicating whether there
is a common intersection between the end of segment
s
i
and the start of segment s
j
.
Trajectory: A trajectory T is a time-ordered se-
quence of pairs of consecutive road segments and
timestamps, represented as T = [⟨s
i
,t
i
⟩]
m
i=1
, where
s
i
∈ S denotes the i-th road segment in the trajectory,
and t
i
is the visit timestamp for s
i
. Trajectories capture
the movement of an object within the road network G.
Representation Learning for Road Networks and
Trajectories: Given a road network G = ⟨S,A
s
⟩ and a
set of historical trajectories D, the objective is to learn
a representation matrix H
s
∈ R
|S|×d
, where the i-th
row, h
s
i
, represents the embedding for road segment
s
i
. Additionally, for each trajectory T ∈ D, we aim to
learn a representation vector h
T
∈ R
d
.
4 PROPOSED TCRLRT METHOD
This section introduces a novel road and trajectory
representation learning model called Time-Aware
Contrastive Representation Learning for Road Net-
work and Trajectory (TCRLRT). Figure 2 overviews
our proposed model. The proposed TCRLRT takes
the road network and trajectory sequence as input.
These inputs are processed through an encoding mod-
ule which consists of a graph encoder (GAT) for road
network representation learning, a sequence encoder
for trajectory encoding, and a temporal encoder. Then
we calculate the loss function with its three com-
ponents which estimate mutual information (MI) for
road-road, trajectory-trajectory, and road-trajectory
pairs. Finally, we jointly maximized these three MI
estimators to obtain the representations.
4.1 Encoding Module
The encoding module includes a graph encoder for
road network representation and a sequence encoder
for trajectory representation. We also use a tempo-
ral encoder to encode temporal information in trajec-
tory representations. We use Graph Attention Net-
works (GATs) (Petar Velickovic and Bengio, 2017)
and a Transformer Encoder (Ashish Vaswani and
Polosukhin, 2017) for graph and sequence encoding,
respectively.
4.1.1 Graph Encoder for Road Segment
Representations
Since road networks are directed graphs, spectral
methods are not suitable. We represent road segments
using GAT:
H
s
= GAT(V
s
,A
s
) (1)
Here, V
s
is the initial embedding matrix for road seg-
ments, A
s
is the adjacency matrix, and H
s
is the out-
VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems
500

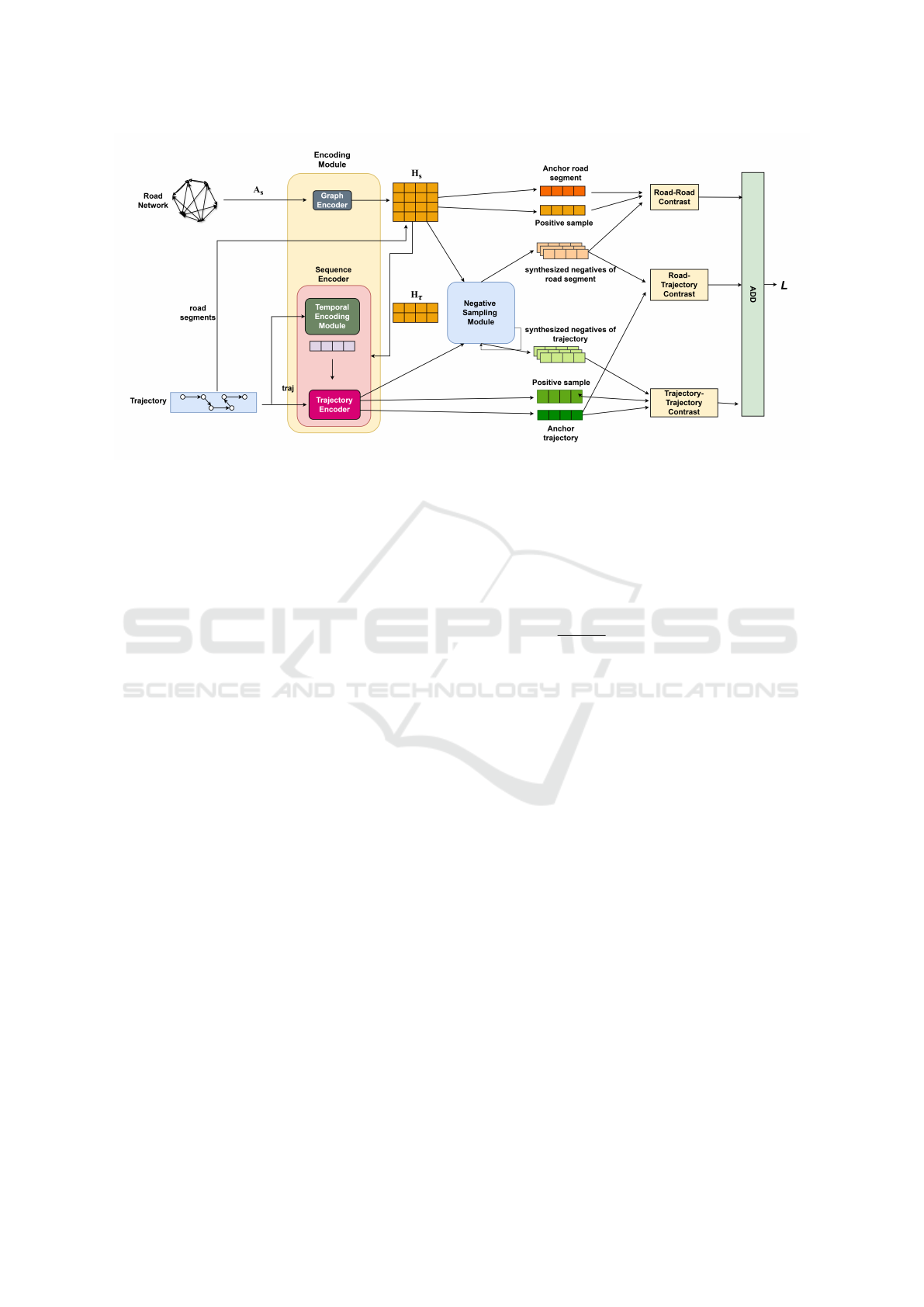
Figure 2: Proposed Time-Aware Contrastive Representation Learning for Road Network and Trajectory Model.
put of the graph encoder, the representation matrix of
the graph with s road segments. The ith row of H
s
is
the representation vector for the road segment in the
road segment set S. GAT enables effective handling
of directed graphs and has demonstrated superior per-
formance.
4.1.2 Sequence Encoder for Trajectory
Representation
Trajectories are encoded as sequences, using
road segment representations to generate a
trajectory representation. Given a trajectory
τ = {(s
1
,t
1
),(s
2
,t
2
),. .. ,(s
n
,t
n
)}, we represent the
input to the sequence encoder as:
H
τ
= {h
s
1
,h
s
2
,. .. ,h
s
n
} (2)
where h
s
i
∈ R
d
is the ith row of H
s
, representing the
embedding of the road segment s
i
in the trajectory.
The input to the sequence encoder, H
τ
, is combined
with T E, the temporal encoding of the time sequence
of the trajectory, in place of traditional positional en-
coding. The sequence encoder processes H
τ
to pro-
duce the final trajectory embedding h
τ
, incorporating
both the structural information from road segments
and the temporal encoding T E to capture the timing
of the trajectory data effectively.
4.1.3 Temporal Encoding
Traditional positional encoding can only represent ba-
sic sequential orders. However, trajectory data in-
volves visit records distributed unevenly across the
temporal axis. Inspired by the work of (Huaiyu Wan
and Lin, 2022), we replace the positional encoding
by creating an encoding with making two significant
modifications: (1) replacing the position indexes with
the prefix sum of time differences of consecutive pairs
in trajectories, and (2) using trainable parameters.
Formally, traditional positional encoding in trans-
formers is defined as:
PE(o) = [cos(ω
1
o),sin(ω
1
o),. .. ,cos(ω
d
o),sin(ω
d
o)]
(3)
where ω
k
=
1
10000
2k/d
, PE represents the positional en-
coding function, o is the position index, ω
k
are the
positional parameters, and 2d is the dimension of the
encoding vector. The limitation of using positional
encoding in trajectory representation is that it does not
accurately capture the temporal sequence of the tra-
jectory. Positional encoding assumes a uniform distri-
bution of positions, which may work well in NLP and
vision tasks where words or image pixels are evenly
spaced. However, the temporal distance between con-
secutive road segments in a trajectory is often non-
uniform. To address this, we use a temporal encoding
defined as:
TE(t) = [cos(ω
1
t),sin(ω
1
t),...,cos(ω
d
t),sin(ω
d
t)]
(4)
Here, TE replaces the position index o with an abso-
lute timestamp t, and the parameters {ω
1
,ω
2
,. .. ,ω
d
}
are set to be trainable. This approach enables the
transformer to capture meaningful temporal distances
between records directly within its encoder. We in-
corporate this temporal encoding into our model by
combining it with the trajectory encoding as follows:
h
τ
= Pool(TransEnc(H
τ
+ TE)) (5)
where TransEnc(·) : R
|τ|×d
→ R
|τ|×d
is the trans-
former encoder applied to the input sequences, fol-
lowed by a mean-pooling operation Pool(·) : R
|τ|×d
→
Time-Aware Contrastive Representation Learning for Road Network and Trajectory
501

R
d
. The outputs H
s
and h
τ
, generated by the GAT and
transformer encoder, respectively, are used as the final
representations of the road network and trajectory.
4.2 Negative Sampling
In contrastive learning, we need an anchor, posi-
tive samples, and negative samples that contribute to
learning the contrast in representations. Positive sam-
ples are typically taken as an augmented or denoised
version of the original anchor. For negative sampling,
methods such as random index-based sampling and
minibatch sampling are commonly used. We adopt a
synthesized negative sampling approach like MOCHI
(Yannis Kalantidis and Larlus, 2020) to create hard
negatives for an effective and optimized representa-
tion learning process. This approach combines pos-
itive samples with some negatives to generate syn-
thetic hard negatives, which helps the model learn
more challenging examples. Given embeddings of
a sample x, we generate synthetic hard negatives by
combining a positive sample x
+
with negative sam-
ples x
−
using a weighted average:
x
mixed
= α · x
−
+ (1 − α) · x
+
(6)
where α is chosen to be between 0.3 and 0.7 to bal-
ance the contribution of positive and negative sam-
ples.
5 CONTRASTIVE LOSS
FUNCTION
The contrastive loss function is designed to optimize
latent space representations by maximizing the mu-
tual information (MI) for positive pairs (related sam-
ples) and minimizing it for negative pairs. We use
the loss function defined by (Zhenyu Mao and Zhao,
2022) as consisting of three components:
Road-Road Contrastive Loss: The road-road con-
trastive loss (L
SS
) measures the MI between each
road segment and its contextual neighbors. The con-
text of a road segment includes structural neighbors,
recorded in adjacency matrices A
s
with a direct con-
nection. Formally, the road-road loss L
SS
is defined
as:
L
SS
= −
1
|S|
∑
s
i
∈S


1
|C(s
i
)|
∑
s
j
∈C(s
i
)
I(h
s
i
,h
s
j
)


(7)
Trajectory-Trajectory Contrastive Loss: The
trajectory-trajectory loss L
T T
is formulated using the
contrastive objective:
L
T T
= −
1
|T |
∑
τ
i
∈T
I(h
τ
′
i
,h
τ
i
) (8)
where τ
′
i
is a noisy version of trajectory τ
i
. Noisy tra-
jectories are generated using techniques such as ran-
dom masking and replacements, along with a ”de-
tour” strategy that replaces part of the trajectory with
an alternative path sharing the same start and end-
points.
Road-Trajectory Contrastive Loss: The road-
trajectory contrastive loss L
ST
is defined as:
L
ST
= −
1
|T |
∑
τ
j
∈T
1
|S|
∑
s
i
∈S
w
τ
j
[s
i
] · I(h
s
i
,h
τ
j
)
!
(9)
where w
τ
[s
i
], representing the RS-T distance, com-
bines the original trajectory length and the length
of an alternative route, providing a flexible ”soft”
weighting for potential positive samples:
w
τ
[s
i
] =
|τ|
|τ
′
| + δ(s
i
,τ)
(10)
Here, δ(s
i
,τ) represents the minimum number of
segments from s
i
to any segment in τ.
Overall Loss Function: The overall loss L is com-
puted as a weighted sum of L
SS
, L
T T
, and L
ST
:
L = λ
SS
· L
SS
+ λ
T T
· L
T T
+ λ
ST
· L
ST
(11)
where the λs are some weight parameters such that
λ
SS
+λ
T T
+λ
ST
= 1. In all cases, the Jensen-Shannon
mutual information estimator is used to enhance sta-
bility against variations in the number of negative
samples.
6 EXPERIMENTS
We evaluate our proposed framework in two real-
world datasets and four traffic-related tasks and com-
pare it with the state-of-art methods.
6.1 Datasets and Preprocessing
The datasets used in this study are provided by the
GAIA project in collaboration with Didi and con-
sist of two months of car-hailing trip data from the
cities of Xi’an and Chengdu, China. Each dataset in-
cludes GPS records for individual trips. Road net-
work data for both cities was gathered from Open
Street Map, and a map-matching algorithm was em-
ployed to align the GPS coordinates to specific road
segments. Through this process, trajectories were
converted into sequences of road segments. To en-
sure quality, we filtered out trajectories that included
fewer than three road segments or had a duration
shorter than one minute. The Xian dataset contains
6,161 road Segments with 15,779 edges, whereas the
VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems
502

same numbers for the Chengdu dataset are 6,632 and
17,038. Average Road Segments per Trip for the Xian
and Chengdu dataset are 31.11 and 30.87 respectively.
6.2 Downstream Tasks and Benchmarks
We conduct four downstream traffic tasks, with two
road segment-based tasks and the other two being
trajectory-based tasks. We compare our method to
several state-of-the-art road and trajectory representa-
tion learning methods, as well as graph representation
learning methods. Methods designed solely for spe-
cific tasks are excluded from the comparison, as we
aim to learn robust representations for various tasks.
Task-specific methods often include tailored repre-
sentations and components, resulting in an inconsis-
tent and unfair comparison.
6.2.1 Road Segment-Based Tasks
To assess the representation of road networks, we fo-
cus on two main tasks: (1) road label classification
and (2) traffic speed prediction.
Road Label Classification: This task is analogous to
node classification in graphs. Road-type labels, such
as motorways and living streets, are collected from
the Open Street Map. The five most common label
types are selected as prediction targets. A classifier
composed of a fully connected layer followed by a
softmax layer is applied to the road segment represen-
tations. The performance is evaluated using Micro-F1
(Mi-F1) and Macro-F1 (Ma-F1) scores.
Traffic Speed Prediction: This is a regression task
where the objective is to predict the average speed on
each road segment, calculated from trajectory data.
A linear regression model is trained using the road
representations, and the evaluation is conducted using
Mean Absolute Error (MAE) and Root Mean Squared
Error (RMSE).
6.2.2 Comparison with Existing Methods
We compare our approach to various advanced road
and graph representation methods:
• Node2Vec: Learns node embeddings by explor-
ing neighborhoods within w-hops through param-
eterized random walks.
• DGI: A contrastive learning approach that max-
imizes the mutual information between node and
graph representations.
• RFN: Builds node and edge representations based
on relational views, using message passing for in-
teraction.
• IRN2Vec: Captures relationships between road
segment pairs using shortest path samples and
multi-objective learning.
• HRNR: Utilizes a hierarchical GNN-based archi-
tecture with three levels to capture structural and
functional properties.
• Toast: Incorporates auxiliary traffic context to
train a skip-gram model and uses a Transformer
module to extract travel-related semantics.
• JCLRNT: JCLRNT applies a unified framework
to learn road network representations by using
within-scale road-road contrast and cross-scale
road-trajectory contrast with an adaptive weight-
ing strategy to optimize road-trajectory represen-
tation.
6.2.3 Trajectory-Based Tasks
To evaluate trajectory representations, we focus on
two main tasks: (1) trajectory similarity search and
(2) travel time prediction.
Trajectory Similarity Search: The objective is to
identify the most similar trajectory to a given query
trajectory from a database. Trajectory representations
are used to calculate similarity scores and rank the
results in descending order. Performance metrics in-
clude Hit Ratio@10 (HR@10) and Mean Rank (MR).
Travel Time Prediction: This task involves predict-
ing the travel time for a given trajectory.
6.2.4 Benchmarks for Trajectory
Representation
The following methods are used as benchmarks for
trajectory representation:
• ParaVec: Learns paragraph embeddings by treat-
ing each trajectory as a paragraph.
• T2Vec: An encoder-decoder model that recon-
structs trajectories from noisy sequences of road
segments using LSTM units.
• Toast: Description already provided in 6.2.1
• GTS: Learns embeddings for points of interest
(POIs) followed by trajectory encoding using a
GNN-LSTM network.
• JCLRNT: Description already provided in 6.2.1
6.3 Simulation Settings
The training dataset comprises 500,000 trajecto-
ries, and we train the model using the Adam opti-
mizer (Kingma and Ba, 2015) with a batch size of 64
over 10 epochs. First, the representation vectors for
Time-Aware Contrastive Representation Learning for Road Network and Trajectory
503

Table 1: Performance Comparison for Road Label Classification and Traffic Speed Inference.
Task Road Label Classification Traffic Speed Inference
Xian Chengdu Xian Chengdu
Mi-F1 ↑ Ma-F1 ↑ Mi-F1 ↑ Ma-F1 ↑ MAE ↓ RMSE ↓ MAE ↓ RMSE ↓
Node2Vec 0.524 0.495 0.586 0.559 7.12 9.00 6.41 8.22
DGI 0.463 0.337 0.475 0.358 6.43 8.41 6.12 7.98
RFN 0.516 0.484 0.577 0.570 6.89 8.77 6.57 8.43
IRN2Vec 0.497 0.458 0.531 0.506 6.52 8.52 6.60 8.59
HRNR 0.541 0.527 0.631 0.609 7.03 8.82 6.52 8.45
Toast 0.602 0.599 0.692 0.659 5.95 7.70 5.71 7.44
JCLRNT 0.637 0.629 0.729 0.701 4.69 6.85 5.02 7.08
Proposed TCRLRT 0.645 0.634 0.742 0.713 4.57 6.78 4.96 7.01
Table 2: Performance Comparison for Similar Trajectory Search and Travel Time Estimation.
Task Similar Trajectory Search Travel Time Estimation
Xian Chengdu Xian Chengdu
MR ↓ HR@10 ↑ MR ↓ HR@10 ↑ MAE ↓ RMSE ↓ MAE ↓ RMSE ↓
Para2vec 216 0.251 279 0.205 220.5 302.7 244.7 345.4
T2Vec 46.1 0.781 38.6 0.806 165.2 240.7 207.5 311.0
Toast 10.1 0.885 13.7 0.905 127.8 190.8 175.6 265.0
GTS 11.0 0.889 12.9 0.896 126.3 186.7 176.1 267.9
JCLRNT 8.87 0.928 9.54 0.912 121.9 179.5 163.6 243.5
Proposed TCRLRT 8.50 0.932 9.10 0.916 120.0 178.2 162.0 241.5
the road segments and trajectories are extracted from
both the benchmark models and our proposed model.
These vectors, standardized to a dimension of 128, are
used in various downstream tasks. The trajectory data
set is split into training and evaluation sets based on
the date, ensuring that there is no overlap. Temporal
sequences are constructed as an absolute time-ordered
sequence with a prefix sum starting at 0. The value of
λ
SS
, λ
T T
, and λ
ST
is found to be optimal at 0.1, 0.1,
and 0.8 respectively. The parameter α for the genera-
tion of negative samples using mixing is set to 0.3, a
lower value is chosen to produce harder samples.
6.4 Results and Analysis
The simulation results for the four tasks are presented
in Tables 1 and 2, with the best results highlighted in
bold. Higher values of Mi-F1, Ma-F1, and HR@10
indicate better performance (↑), while lower values
of MAE, RMSE, and MR indicate better performance
(↓). General methods such as Node2vec, DGI and
Para2Vec perform poorly, as they do not capture the
unique characteristics of road networks and trajecto-
ries. Methods like IRN2Vec and T2Vec perform bet-
ter due to their richer contextual information. Toast
and GTS show improvements in travel-time estima-
tion and trajectory retrieval. JCLRNT employs con-
trastive learning but does not consider temporal mod-
eling. Our approach incorporates temporal informa-
tion and a hard negative sampling strategy to optimize
training, outperforming JCLRNT and other baselines.
7 CONCLUSIONS
In this paper, we proposed a model of representa-
tion learning for road networks and trajectories. Our
approach introduces an end-to-end framework that
jointly learns road network and trajectory represen-
tations, incorporating a learnable temporal encoding
and synthesizing harder negatives for optimized train-
ing. We conducted experiments on two real-world
datasets, evaluating the model on four downstream
tasks: two focused on road segments and two on tra-
jectories. For future work, we plan to enhance hard
negative sampling techniques specifically tailored for
road network and trajectory-based tasks. We also plan
to incorporate more modalities of features like text
and images to model the representation learning with
heterogeneous graphs.
REFERENCES
Ashish Vaswani, Noam Shazeer, N. P. J. U. L. J. A. N. G.
L. K. and Polosukhin, I. (2017). Attention is all you
need. CoRR, abs/1706.03762.
Grover, A. and Leskovec, J. (2016). node2vec: Scal-
VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems
504

able feature learning for networks. In Proceedings
of the 22nd ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining, page
855–864. Association for Computing Machinery.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Comput., 9(8):1735–1780.
Huaiyu Wan, Yan Lin, S. G. and Lin, Y. (2022). Pre-
training time-aware location embeddings from spatial-
temporal trajectories. IEEE Transactions on Knowl-
edge and Data Engineering, 34(11):5510–5523.
Jiawei Jiang, Dayan Pan, H. R. X. J. C. L. and Wang,
J. (2023). Self-supervised trajectory representation
learning with temporal regularities and travel seman-
tics. In 39th IEEE International Conference on Data
Engineering, ICDE 2023, Anaheim, CA, USA, April
3-7, 2023, pages 843–855. IEEE.
Joshua Robinson, Ching-Yao Chuang, S. S. and Jegelka, S.
(2020). Contrastive learning with hard negative sam-
ples. ArXiv, abs/2010.04592.
Kingma, D. P. and Ba, J. (2015). Adam: A method for
stochastic optimization. In 3rd International Confer-
ence on Learning Representations, ICLR 2015, San
Diego, CA, USA, May 7-9, 2015, Conference Track
Proceedings.
Meng-xiang Wang, Wang-Chien Lee, T.-y. F. and Yu, G.
(2019). Learning embeddings of intersections on road
networks. In Proceedings of the 27th ACM SIGSPA-
TIAL International Conference on Advances in Ge-
ographic Information Systems, pages 309–318, New
York, NY, USA. Association for Computing Machin-
ery.
Ning Wu, Xin Wayne Zhao, J. W. and Pan, D. (2020).
Learning effective road network representation with
hierarchical graph neural networks. In Proceedings
of the 26th ACM SIGKDD International Conference
on Knowledge Discovery & Data Mining, pages 6–
14, New York, NY, USA. Association for Computing
Machinery.
Peng Han, Jin Wang, D. Y. S. S. and Zhang, X. (2021). A
graph-based approach for trajectory similarity compu-
tation in spatial networks. In Proceedings of the 27th
ACM SIGKDD Conference on Knowledge Discovery
and Data Mining, pages 556–564, Virtual Event, Sin-
gapore. Association for Computing Machinery.
Petar Velickovic, Guillem Cucurull, A. C. A. R. P. L. and
Bengio, Y. (2017). Graph attention networks. ArXiv,
abs/1710.10903.
Philip Bachman, R. D. H. and Buchwalter, W. (2019).
Learning Representations by Maximizing Mutual In-
formation Across Views, pages 1–11. Curran Asso-
ciates Inc., Red Hook, NY, USA.
Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M.,
and Monfardini, G. (2009). The graph neural net-
work model. IEEE Transactions on Neural Networks,
20(1):61–80.
Ting Chen, Simon Kornblith, M. N. and Hinton, G. (2020).
A simple framework for contrastive learning of visual
representations. In Proceedings of the 37th Interna-
tional Conference on Machine Learning, pages 1–11.
JMLR.org.
Tobias Skovgaard Jepsen, C. S. J. and Nielsen, T. D. (2019).
Graph convolutional networks for road networks. In
Proceedings of the 27th ACM SIGSPATIAL Interna-
tional Conference on Advances in Geographic Infor-
mation Systems, pages 460–463, New York, NY, USA.
Association for Computing Machinery.
Velickovic, P., Fedus, W., Hamilton, W. L., Li
`
o, P., Bengio,
Y., and Hjelm, R. D. (2019). Deep graph infomax. In
7th International Conference on Learning Represen-
tations, ICLR 2019, New Orleans, LA, USA, May 6-9,
2019. OpenReview.net.
Xiucheng Li, Kaiqi Zhao, G. C. C. S. J. and Wei, W. (2018).
Deep representation learning for trajectory similarity
computation. In 2018 IEEE 34th International Con-
ference on Data Engineering (ICDE), pages 617–628.
IEEE.
Yangxin Lin, P. W. and Ma, M. (2017). Intelligent trans-
portation system (its): Concept, challenge and oppor-
tunity. In 2017 IEEE 3rd International Conference on
Big Data Security on Cloud (BigDataSecurity), IEEE
International Conference on High Performance and
Smart Computing (HPSC), and IEEE International
Conference on Intelligent Data and Security (IDS),
pages 167–172. IEEE.
Yannis Kalantidis, Mert B
¨
ulent Sariyildiz, N. P. P. W. and
Larlus, D. (2020). Hard negative mixing for con-
trastive learning. In Advances in Neural Information
Processing Systems 33: Annual Conference on Neural
Information Processing Systems 2020, NeurIPS 2020,
December 6-12, 2020, virtual. NeurIPS.
Yile Chen, Xiucheng Li, G. C. Z. B. C. L. Y. L. A. K. C.
and Ellison, R. (2021). Robust road network repre-
sentation learning: When traffic patterns meet travel-
ing semantics. In Proceedings of the 30th ACM Inter-
national Conference on Information and Knowledge
Management, pages 211–220, Virtual Event, Queens-
land, Australia. Association for Computing Machin-
ery.
Yoshua Bengio, A. C. and Vincent, P. (2013). Representa-
tion learning: A review and new perspectives. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 35(8):1798–1828.
Yu Zheng, Lizhu Zhang, X. X. and Ma, W.-Y. (2009). Min-
ing interesting locations and travel sequences from
GPS trajectories. In Proceedings of the 18th Inter-
national Conference on World Wide Web, pages 791–
800, Madrid, Spain. Association for Computing Ma-
chinery.
Zhenyu Mao, Ziyue Li, D. L. L. B. and Zhao, R. (2022).
Jointly contrastive representation learning on road net-
work and trajectory. In Proceedings of the 31st ACM
International Conference on Information & Knowl-
edge Management, pages 1501–1510, New York, NY,
USA. Association for Computing Machinery.
Time-Aware Contrastive Representation Learning for Road Network and Trajectory
505