Pseudorandom Number Generators, Perfect Learning and Model

Visualization with Neural Networks: Expanding on LFSRs and Geffe

Sara Boanc

Babes¸-Bolyai University, Cluj-Napoca, Romania

Keywords:

Pseudorandom Number Generators, Neural Networks, Visualization, Linear Feedback Shift Registers, Geffe.

Abstract:

The present paper explores the use of Artiﬁcial Neural Networks in the context of Pseudorandom Number

Generators such as Linear Feedback Shift Registers and Geffe. Because of their hardware efﬁciency, variations

of these generators may be used by IoT devices for security purposes. Testing to ensure security is essential,

but it was observed that traditional test suites are too slow for the task. Machine Learning models, on the

other hand, represent a faster alternative. While Artiﬁcial Neural Networks have been able to learn from these

generators, improvements are still needed in terms of optimization and lowering domain knowledge. For that,

the present paper focuses on the manner in which state of the art neural network approaches scale for a wider

variety of Linear Feedback Shift Registers, including some of degree ≥ 100 and discusses the challenges

that arise. Moreover, it proposes a novel Geffe learning approach that produces up to 100% testing accuracy

and, based on that, promotes an additional optimization by capitalizing on model visualization and the ability

of neural networks to learn deterministic functions to perfection. A comparative analysis is performed in

order to show the superiority of the approach and an in-depth discussion is conducted on the possibility and

implications of neural network perfect learning, particularly when coupled with model visualization. The

obtained results can be regarded as incremental advances towards the creation of more robust neural network

models to perform PRNG security evaluation for IoT devices.

1 INTRODUCTION

Recent years have seen an increase in the use of Ma-

chine Learning techniques for detecting latent pat-

terns in Pseudorandom Number Generators (PRNGs).

It is believed that a Machine Learning algorithm that

is able to learn from a pseudorandom sequence to

the point of predicting future outputs with more than

chance accuracy has captured at least some of the in-

trinsic, hidden mechanisms of the PRNG. Learning is

possible because, while PRNGs produce numeric se-

quences that have a random aspect, they rely on the

repetitive application of some mathematic and logic

operations to produce new outputs, therefore causing

the existence of some subtle patterns.

Given the suitability of Machine Learning tech-

niques for handling large amounts of numerical data,

several successful applications for predicting future

PRNG outputs have surfaced in the literature (Kant

and Khan, 2006), (Fischer, 2018), (Mostafa Hassan,

2021), (Amigo et al., 2021). The most prominent ap-

proaches are those that rely on neural networks.

Machine and Deep Learning approaches have

been extensively discussed with respect to the pos-

sibilities they bring to the ﬁeld of IoT (Cui et al.,

2018) (Hussain et al., 2020) as well. Recent work

(Ince, 2024) has revealed that neural networks can

successfully mimic traditional PRNG test suites while

signiﬁcantly decreasing evaluation time on IoT de-

vices. Linear Feedback Shift Register (LFSR) in-

spired PRNGs are used for generating randomness in

the context of IoT (Noura et al., 2019). While (Ince,

2024) used neural networks only to imitate statistical

tests, it is considered that these techniques are able

to discover other patterns in PRNG data that tradi-

tional test suites may miss. The creation of Machine

Learning speciﬁc tests for PRNGs used in IoT devices

may be beneﬁcial for combining fast and robust eval-

uation. However, since some of the PRNGs used in

the context of IoT, such as stream ciphers (Kietzmann

et al., 2021), have not been successfully predicted us-

ing Machine Learning techniques (Kant et al., 2009),

we observe the need for advancing the possibilities

imposed by the latter, especially of neural networks,

in the perspective of leading to solutions that will, in

the future, be able to successfully learn from more

Boanc

a, S.

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe.

DOI: 10.5220/0013298500003944

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Internet of Things, Big Data and Security (IoTBDS 2025), pages 117-128

ISBN: 978-989-758-750-4; ISSN: 2184-4976

117

complex PRNGs. We conjecture that once this is pos-

sible, Machine Learning testing frameworks will be

more robust and lead to a more realistic evaluation of

elaborate PRNGs. In the present work we aim to take

an incremental approach in this direction by focus-

ing on extending current possiblities of learning from

LFSR-based PRNGs with Artiﬁcial Neural Networks

(ANNs).

We observe that in (Boanc

a, 2024)(a) ANNs were

used for ﬁnding the smallest possible size for a train-

ing set that allows learning from LFSRs and for cre-

ating a pipeline to tackle the Geffe PRNG prediction

problem. While the proposed directions were able to

mitigate several difﬁculties imposed by LFSRs and

Geffe, we identify possibilities of further optimiza-

tion and improvement. We observe that (Boanc

2024)(a) failed to evaluate the manner in which the

proposed ANN framework scales for higher degree

LFSRs (≥ 100) where the binary output distribution

may be skewed towards 0. Moreover, the pipeline

model proposed for Geffe in (Boanc

a, 2024)(a) re-

quires signiﬁcant domain knowledge as it evaluates

its consisting LFSRs separately.

The present paper focuses on deriving optimiza-

tions for learning from LFSRs and Geffe with ANNs

with the goal of developing lightweight and reliable

Machine Learning models that may ultimately be

used to evaluate the security of PRNGs on IoT de-

vices. It addresses the aforementioned issues by eval-

uating the approach proposed in (Boanc

a, 2024)(a)

for LFSRs degree ≥ 100 and discussing the chal-

lenges that arise in this context. Furthermore, a direct

ANN model is introduced for making predictions on

complete Geffe seeds, without the need of a special-

ized pipeline. This model is then used to derive an

optimization by capitalizing on visualization and the

ANNs ability of learning deterministic functions to

perfection. The proposed Geffe models are compara-

tively evaluated against the one in (Boanc

a, 2024)(a).

A discussion ensues about the capability of ANNs to

perfectly learn deterministic functions in the context

of PRNGs and the possibilities advanced by it, espe-

cially when corroborated with visualization. More-

over, the paper addresses the possibility of extending

the current approach to learn from Geffe outputs in

an attempt to lower the number of bits needed for the

task in (Kant et al., 2009). The results are regarded

from the perspective of learning on more complex

PRNGs used in IoT devices such as stream ciphers.

Challenges that arise in this respect are discussed.

The rest of the paper is organized as follows. Sec-

tion 2 presents an overview of the related work. Sec-

tion 3 offers theoretical background for the proposed

approach. Section 4 presents the experiments. Sec-

tion 5 describes the obtained results. Section 6 fol-

lows with a discussion regarding the results and impli-

cations of the employed methods. Section 7 presents

the conclusion of the paper.

2 RELATED WORK

Machine Learning methods have been successfully

employed for a wide range of cryptography related

tasks, such as differential cryptanalysis (Gohr, 2019)

and pseudorandom number generation (Pasqualini

and Parton, 2020). While the established method

for PRNG security evaluation is the use of statisti-

cal test suites such as NIST (Rukhin et al., 2001),

TestU01 (L’Ecuyer and Simard, 2007) or dieharder

(Robert G. Brown, 2017), discovering hidden patterns

which may undermine PRNG security with the use

of Machine Learning, especially neural networks, has

evolved in recent years. Given the ability of neural

networks to use and obtain reliable results for large

amounts of data, (Fischer, 2018) proposed a recur-

rent neural network paradigm for evaluating a set of

PRNGs, including some that claim to be cryptograph-

ically secure. While certain interest had been invested

into this problem in the past (Savicky and Robnik-

Sikonja, 2008), the results of the former produced re-

newed engagement in the Machine Learning commu-

nity and since, a number of other approaches have sur-

faced, tackling problems such as next in sequence pre-

diction (Feng and Hao, 2020), (John Labelle, 2020),

(Amigo et al., 2021), (Prashant Limba, 2024), min-

entropy estimation (Truong et al., 2018), (Lv et al.,

2020) (Li et al., 2020) and inversion (Mostafa Hassan,

2021). In a comprehensive study, (Boanca, 2024)(b)

gathered a variety of such approaches in order to high-

light advances and popularize this emerging niche.

The study observed the difﬁculty of the problem (as

some approaches (Zanin, 2022) failed to produce re-

sults at all) and proposed a number of directions. Par-

ticularly, it admitted the possibility of PRNG simpli-

ﬁcation and that of performing learning to perfection

due to the deterministic nature of the PRNGs.

In the direction of IoT, the use of Machine and

Deep Learning techniques has been steadily docu-

mented (Cui et al., 2018), (Hussain et al., 2020). Cap-

italizing on the ability of neural networks to mitigate

the high evaluation time needed by traditional statis-

tical tests, (Ince, 2024) proposed a Deep Learning

framework to replace them for IoT devices. A variety

of PRNGs that originate from LFSRs are used in the

context of IoT (Noura et al., 2019), (Kietzmann et al.,

2021). In its early stages, the task of predicting sub-

sequent bits from LFSRs with Machine Learning was

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

118

approached from the perspective of Decision Trees

(DTs) (Kant and Khan, 2006). Subsequently, (Kant

et al., 2009) extended the DT approach to Geffe and

other PRNGs achieving up to 100% accuracy. How-

ever, it stressed the fact that neural network models

may need higher amounts of data in order to obtain

competitive results. (Gupta et al., 2021) and (Kim

and Kim, 2021) managed to elevate the problem of

making predictions on LFSRs to the use of ANNs.

This was done in order to ﬁnd a minimal bound for

the number of bits necessary to generate LFSR pat-

terns (Gupta et al., 2021) and the minimum window

size needed for learning (Kim and Kim, 2021). More

speciﬁcally, (Gupta et al., 2021) introduced two pat-

tern generation algorithms that enabled the creation

of a large dataset consisting of 10

instances from a

small number of known LFSR bits. Using this ap-

proach, the authors managed to learn from and pre-

dict LFSRs with up to 100% accuracy using fewer

bits than the Berlekamp-Massey algorithm (Massey,

1969). In (Kim and Kim, 2021), the minimum win-

dow size needed for learning was revealed to be equal

to the LFSR degree. (Boanc

a, 2024)(a) provided ad-

ditional optimizations by ﬁnding a lower bound for

the actual number of instances necessary for creat-

ing the ANN training dataset (less than 10

instances)

even for LFSRs of degree > 50. The author corrob-

orated this optimization and the nature of the Geffe

PRNG, which consists of 3 separate LFSRs, in or-

der to create an optimized pipeline model that is able

to learn from Geffe using an end-to-end ANN ap-

proach. As the only other known approach for learn-

ing Geffe (Kant et al., 2009) used millions of bits, the

pipeline proposed in (Boanc

a, 2024)(a) succeeded in

contradicting the claim that ANNs need more data for

training when compared to DTs and cemented ANNs

as the most efﬁcient tool for learning on LFSRs and

Geffe.

It is identiﬁed, however, that the work in (Boanc

2024)(a) can still be improved. More speciﬁcally, the

proposed optimization for LFSR learning, namely the

reduction of the magnitude degree of the training set

size to 10

needs to be evaluated as it scales for LF-

SRs of degree ≥ 100. Moreover, given the excessive

domain knowledge needed by the developed pipeline

(each LFSR is delimited within the Geffe seed and

evaluated separately), a more direct approach should

be explored.

In this respect, the contributions of the present pa-

per are summarized as follows:

• Explore how optimizations presented in (Boanc

2024)(a) scale for other LFSRs, including some

of degree ≥ 100 (higher LFSR degrees are chal-

lenging due to having an unbalanced binary out-

put distribution with a preference towards 0);

• Train an ANN model on Geffe seeds to predict the

next Geffe outputs;

• Compare the obtained results to other Geffe learn-

ing approaches;

• Derive an optimization for Geffe prediction using

model visualization;

• Expand on the implications of perfect learning of

deterministic functions in the context of neural

networks and PRNGs;

• Evaluate the possibility of ANN learning from

more complex expressions of PRNGs.

3 THEORETICAL BACKGROUND

The present section introduces the theoretical back-

ground for learning from PRNGs, more speciﬁcally

LFSRs and Geffe, with neural networks (ANNs). In

the beginning, a prefacing discussion is revealed for

better understanding the intended role of ANNs in

predicting PRNGs. After that, the remaining sec-

tion is split in two subparts: the ﬁrst, introducing the

PRNGs; the second, presenting ANNs.

3.1 Pseudorandom Number Generators

and Neural Networks: Introductory

Discussion

Pseudorandom Number Generators are algorithms

that produce sequences of numbers that appear to be

uncorrelated with one another, yet are the result of a

deterministic process.

Because of their unpredictability, PRNGs are gen-

erally used in the context of cryptographic applica-

tions, which demand high quality randomness (that is,

highly unpredictable PRNGs) but also in simulation

and games, where the conditions for unpredictability

tend to be more lax.

Thus far, statistical tests have been employed for

evaluating PRNG security by investigating repetitive

patterns and regularities that may account for higher

than chance prediction accuracy in certain contexts.

As such tests have been developed and used for a few

decades, they have improved to the point of ensuring

a reliable degree of security. Machine Learning tech-

niques, and more speciﬁcally neural networks, have

seen a relative more recent development. Thus, even

though, in theory, neural networks are believed to be

able to identify patterns that traditional statistical tests

might miss, it is still too early in their development to

produce results for highly complex PRNGs. It can be

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe

119

seen in the literature how a number of simpler PRNGs

such as Linear Congruential Generators and LFSRs

provide the “favorite” toy data material for challeng-

ing these innovative techniques.

While important development has already been

achieved, further steps need to be taken from a Ma-

chine Learning, and particularly neural network, per-

spective in order to enable such techniques to tackle

more complex problems. For now, an exhaustive ex-

ploration of their possibilities in the context of sim-

pler PRNGs, such as LFSRs and Geffe, especially

with an interest towards visualization and optimiza-

tion, is considered a steady stepping block for attain-

ing meaningful results for more complex PRNGs in

the future. We theorize that it may be better to obtain

high precision results for simpler PRNGs with a focus

on optimization, than to achieve mediocre results for

more complex ones, as the former may pave the way

for improving the latter.

In what follows, the currently studied PRNGs,

namely LFSRs and the Geffe generator are described.

3.2 Linear Feedback Shift Registers:

Seed, Taps, Degree and Primitive

Polynomial

Linear Feedback Shift Registers are PRNGs that pro-

duce random numbers based on a series of logic op-

erations (XOR) applied upon their seed (Schneier,

2007).

The seed of a PRNG is the internal, usually se-

cret, state of that generator, which may be manu-

ally initialized with a starting value. It is through a

series of operations performed on that seed that the

PRNG changes its internal state and is able to out-

put seemingly random numbers. However, because

of the fact that the exact same sequence of operations

is used to alter successive hidden states (or seeds),

some regularity may be perceived in the PRNG output

(Schneier, 2007).

For LFSRs, the seed consists of a series of bits. At

each time step, the LFSR is clocked, meaning a new

bit is added to the leftmost position in the seed, the

remaining bits are shifted to the right and the right-

most bit is output. The bit that is added is the result of

successive XOR operations applied on bits situated at

tap positions within the seed (Schneier, 2007).

Tap positions or more simply taps are certain po-

sitions or indices of the LFSR seed that are outlined in

its describing primitive polynomial (Schneier, 2007).

A primitive polynomial is a polynomial modulo 2

that describes the conﬁguration of a LFSR. For ex-

ample, x

+ x

+ 1 is the primitive polyno-

mial of degree 8 that describes the LFSR having state

00011101, where 1s are placed on positions 8, 6, 5,

4, like the powers of the polynomial. The XOR op-

eration will be performed on bits on position 8 and

6, then the result will be XOR-ed with the bit on po-

sition 5 and their result will be XOR-ed with the bit

on position 4 to obtain a new bit that will, in turn,

be used to change the LFSR seed conﬁguration. The

same operation is repeated until enough data has been

gathered from the LFSR or until the LFSR cycles (the

seed conﬁguration returns to its original state).

This particular rule in the evaluation and the

formation of consecutive LFSR seeds describes Fi-

bonacci LFSRs. For simplicity, in what follows we

will term them as simply LFSRs (Schneier, 2007).

As at each step LFSRs output a single bit value,

they may be seen as Pseudorandom Bit Generators

and this is the perspective from which they are ap-

proached in the current study. However, it is impor-

tant to note that it is possible to use the generated bits

to derive actual numbers.

3.3 Geffe

PRNG aggregation is the technique of combining

the outputs (and thus, the mechanisms) of different

PRNGs in a manner that allows for obtaining a new,

more robust one. This is the premise for the creation

of the Geffe PRNG.

Geffe uses 3 LFSRs that operate independently

and, based on their outputs, derives a pseudorandom

bit that will be the ﬁnal Geffe output. The Geffe for-

mula is described as follows:

= (x

∧ x

) ⊕ (¬x

∧ x

) (1)

where x

is the Geffe output and x

, x

and x

are

the corresponding outputs of the 3 LFSRs (Schneier,

2007).

It is known that the Geffe output is highly corre-

lated to the output of the third LFSR, x

, as they share

the same values in 75% of the cases (Schneier, 2007).

This is perceived as a severe limitation to Geffe, since

the problem of predicting it with more than chance

accuracy is reduced to the problem of predicting the

output of the third LFSR, rendering the aggregation

useless (Schneier, 2007).

While in certain circumstances traditional ap-

proaches to predicting Geffe may need as little as

37d

max

bits, where d

max

is the degree of the largest

LFSR (Schneier, 2007), Machine Learning based ap-

proaches tend to struggle at this task.

3.4 Artiﬁcial Neural Networks

Artiﬁcial Neural Networks are a powerful type of Ma-

chine Learning techniques that are known as universal

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

120

approximators of functions. That is, given some in-

put, they should be able to learn an approximate map-

ping to its corresponding output.

At their core, ANNs are algorithms that use aggre-

gation of data (dot product) and unit activation (ac-

tivation functions) to perform this task. The paral-

lelism with the human brain comes from their percep-

tive abilities (they are fed some input, thus we say

they are able to “perceive” it) and the error correction

mechanism (backpropagation), similar to trial and er-

ror learning for humans.

In more technical terms, ANNs consist of neurons

that share weighted connections and are disposed in

layers such that all neurons in consecutive layers are

fully connected to one another, but neurons in the

same layer are not.

As an input of the form I = (i

,...,i

) is fed into

the network, neural units compute the dot product be-

tween the input and their corresponding weights:

z = i

+ i

+ ...i

+ b (2)

where w

,...w

is the set of weights and b is the

bias of the neuron.

The resulting z value is activated via an activation

function that is typically non-linear, such as relu, tanh

and sigmoid: h = σ(z) (here, sigmoid has been used)

to obtain the ﬁnal output of the neuron, which will,

in turn, be the input of other neurons in the following

layer.

This process is repeated until it reaches the output

layer, where the error function is computed. The er-

ror is propagated backwards into the network with the

goal of adjusting all neural weights (and biases) ac-

cordingly. The backpropagation process relies upon

derivatives. As the current weight conﬁguration may

describe a point on the error function in a hyperplane,

minimizing the error equates to performing a step by

step descent on the error space from the current point.

In order to perform this descent, we need to know the

slope (hence the derivative) of the error function, such

that we may move downwards.

The forward propagation of the information and

the backpropagation of the error is repeated until no

more improvement (or learning) is possible.

Figure 1 displays an ANN with an input layer, one

hidden layer and one output layer.

Given their ability to capture signiﬁcant features

when learning from the data, ANNs are a robust tool

for predicting LFSR-based PRNGs (Mostafa Hassan,

2021), (Gupta et al., 2021), (Kim and Kim, 2021),

(Boanc

a, 2024)(a), which is the reason why they have

been chosen for the task.

Figure 1: A simple ANN consisting of an input layer, a hid-

den layer with 2 neurons and an output layer with 1 neuron.

For simplicity, biases have been omitted.

4 EXPERIMENTS

The following section describes the experiments per-

formed as part of the current paper.

Unless speciﬁed otherwise, all experiments have

been undertaken using a CPU based Google Colab

backend. The use of CPU instead of GPU is motivated

by the fact that CPU was found to perform better for

smaller tensor dimensions.

4.1 Linear Feedback Shift Registers

While (Boanc

a, 2024)(a) managed to reduce the num-

ber of bits needed to learn from LFSRs with ANNs to

degree of magnitude 10

, this bound was evaluated

only for LFSRs of degree < 100. In an attempt to

test the scalability of the solution for other LFSRs,

including some of degree ≥ 100, we observe the con-

ﬁgurations presented in Table 1.

Table 1: Conﬁgurations of the studied LFSRs.

Degree Primitive polynomial Nb. of taps

42 x

+ x

+ 1 4

46 x

+ x

+ 1 4

100 x

100

+ x

+ 1 2

155 x

155

+ x

+ 1 2

177 x

177

+ x

+ 1 2

250 x

250

+ x

+ 1 2

The dataset is created in the following manner: a

sliding window of size LFSR degree + 1 is moved

bit by bit across LFSR outputs, resulting in binary

input vectors of length LFSR degree and binary out-

put labels corresponding to the value of bit at position

LFSR degree + 1. Given the nature of ANN learning

and its sensitivity towards statistical bias it is essential

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe

121

that the obtained output labels are evenly distributed

among classes 0 and 1.

We observe that in the case of LFSR learning, the

only positions in the input vector that inﬂuence the

output are the tap positions, the rest of the bits be-

ing considered noise. More precisely, in the case of

LFSRs degree ≥ 100, only 2 values in the input vec-

tor are relevant. The possibilities of combining the 2

relevant bit values at tap positions for LFSRs degree

≥ 100 are limited: 0 XOR 0 and 1 XOR 1 result in

a ﬁnal value of 0; 0 XOR 1 and 1 XOR 0 result in a

ﬁnal value of 1.

In what follows, we will address the aforemen-

tioned combinations of bits at these relevant tap po-

sitions as LFSR patterns. For each pattern, 00, 01,

10, 11, a number of input vectors can be associated to

it, namely the vectors that have these speciﬁc bit con-

ﬁgurations at tap positions. We observe that because

of the large distance between tap positions in LFSRs

degree ≥ 100, the patterns are unevenly skewed to-

wards those that result in an output of 0 (00 and 11),

thus making data unbalanced. Figure 2 displays the

distribution in terms of the aforementioned patterns

for LFSRs degree ≥ 100 for the ﬁrst 5 × 10

dataset

entities.

It is apparent that the dataset needs to be prepro-

cessed such that an even number of entities is present

for each pattern. Through visualization we observe

the number of available entities per pattern for each

LFSR degree ≥ 100. A balanced number of entities

is extracted from each LFSR pattern as presented in

Table 2. For LFSRs degree < 100, no extra process-

ing step is necessary since contiguous bits account for

balanced classiﬁcation labels. For them, the training

set simply used the ﬁrst 8000+degree+1 LFSR bits,

as in (Boanc

a, 2024)(a).

Table 2: Number of training samples for the studied LFSR.

Degree Entities / pattern Total samples

42 not the case 8000

46 not the case 8000

100 2000 8000

155 2000 8000

177 2500 10000

250 4000 12000

These observations come to challenge the assump-

tion in (Boanc

a, 2024)(a), since for LFSRs degree

≥ 100 a number of bits greater than order of magni-

tude 10

was necessary to create the training set. The

assumption in (Boanc

a, 2024)(a) was that contiguous

bits (with N − 1 bit overlap, where N is the sliding

window size) could be used to generate the training

set. In the case of LFSRs degree ≥ 100, this assump-

Figure 2: Pattern distribution for LFSRs degree ≥ 100.

tion may not hold since contiguous bits may skew data

distribution towards the dominant class (i. e. class 0).

Thus, after collecting enough samples for that class

using the sliding window mechanism, inputs that lead

to the same output need to be skipped. Consequently,

an N − 1 overlap may not be applied to all instances

because some of their consecutive outputs (equal to 0)

may be dropped for keeping the training set balanced.

Thus, a training set of 8000 samples (as in the case of

LFSR degree 155) requires more than 8000 + 155 + 1

LFSR output bits to be created. Experimentally, it

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

122

was observed that a number of bits equal to degree

of magnitude 10

to 10

was necessary for deriving

a balanced number of patterns (and thus, of training

inputs) for LFSRs degree ≥ 100.

For each of the validation and test sets, 1000 sam-

ples have been obtained in a similar manner.

The architecture of the proposed ANN is similar

to the one used in (Boanc

a, 2024)(a), namely 2 lay-

ers consisting of 10 and 1 neurons, respectively, with

sigmoid activation. Binary cross-entropy was used as

loss function. The number of epochs was chosen to be

250 for LFSRs degree < 100 as in (Boanc

a, 2024)(a)

and 500 for LFSRs degree ≥ 100 and the batch size

64.

4.2 Geffe

4.2.1 Learning from Consecutive Seeds

Instead of using a processing pipeline which sep-

arately considers each Geffe seed LFSR (Boanc

2024)(a), we formulate the problem of learning from

Geffe seeds directly. In this manner, we aim to reduce

domain knowledge, which is one of the limitations in

the study of (Boanc

a, 2024)(a).

The dataset is composed by input entries which

consist of full Geffe seed conﬁgurations (i. e. the

concatenated seed conﬁgurations of its consisting LF-

SRs) and the corresponding output bit as a binary la-

bel. For each Geffe conﬁguration 8000 samples are

used for training, 2000 for validation and 2000 for

testing. The only exception is the conﬁguration where

the LFSR degree 250 is present. For that, 12000 sam-

ples were used for training, 1000 for validation and

1000 for testing.

The ANN architecture consists of 6 layers of sizes

input

size− 64− 32 − 16 − 8 − 1 having sigmoid acti-

vation. The loss function used is binary cross-entropy.

Models are trained for 50 to 100 epochs with batch

sizes of 16 for Geffe conﬁgurations where all LFSRs

have degree < 100 and 64 for those that contain a

LFSR degree ≥ 100. The Geffe conﬁgurations and

data sizes used for training, validation and testing as

well as the corresponding batch size and number of

training epochs are presented in Table 3.

4.2.2 Learning from Consecutive Outputs

We further elaborate on the problem and attempt to

eliminate the need for domain knowledge completely

through ANN learning from Geffe outputs only. A

simple conﬁguration with LFSRs degree 8,13,19 is

studied, where the LFSR degree 8 is described by

primitive polynomial x

+1 and LFSRs

degree 13 and 19 are taken from (Boanc

a, 2024)(a).

Table 3: Conﬁgurations and corresponding number of train,

validation and test samples as well as the batch size (de-

noted Bs.) and total training epochs (denoted Ep.) for the

Geffe models. The conﬁguration is represented only by the

degree of each LFSR. In the case of LFSRs degree < 100

which were not deﬁned in the present paper, the conﬁgura-

tion follows the same parameters as in (Boanc

a, 2024)(a).

Conﬁg. Train Valid. Test Bs. Ep.

19,42,53 8000 2000 2000 16 50

19,42,59 8000 2000 2000 16 50

19,46,53 8000 2000 2000 16 50

19,46,59 8000 2000 2000 16 50

19,53,59 8000 2000 2000 16 50

42,53,59 8000 2000 2000 16 50

46,53,59 8000 2000 2000 16 50

19,53,100 8000 2000 2000 64 100

42,59,155 8000 2000 2000 64 50

46,53,177 8000 2000 2000 64 100

53,59,250 12000 1000 1000 64 50

Data is obtained through a sliding window process

over consecutive Geffe binary outputs, with a win-

dow size equal to lcm(D

LFSR1

LFSR2

LFSR3

) + 1,

where lcm denotes the lowest common multiple of the

degrees (D) of the 3 LFSRs in the Geffe conﬁgura-

tion and the +1 term accounts for its corresponding

output (to be used as binary label). The choice of

the window size is based on the conclusions of (Kant

et al., 2009). The dataset that ensues is composed of

175 × 10

training samples and 1000 validation and

testing samples, respectively.

Multiple deep ANN architectures are proposed,

having at least the complexity of the one used for

learning from Geffe seeds. Sigmoid activation is

used, binary cross-entropy is chosen as loss function

and the model is trained on a GPU with a batch size

of 2048 for 1000 epochs.

5 RESULTS

5.1 Linear Feedback Shift Registers

The ANN models trained on LFSRs produce highly

accurate results, demonstrating ability at the level of

(almost) perfectly ﬁtting the data. As it will be ex-

panded upon in Section 6, this is not equivalent to

overﬁtting, especially as some ANN models achieve

perfect accuracy on the testing sets as well. Table 4

provides an overview of the corresponding testing ac-

curacy for each of the studied LFSR conﬁgurations.

The number of bits needed for training was ob-

served to increase together with the degrees of the

LFSRs having an upper bound at order of magnitude

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe

123

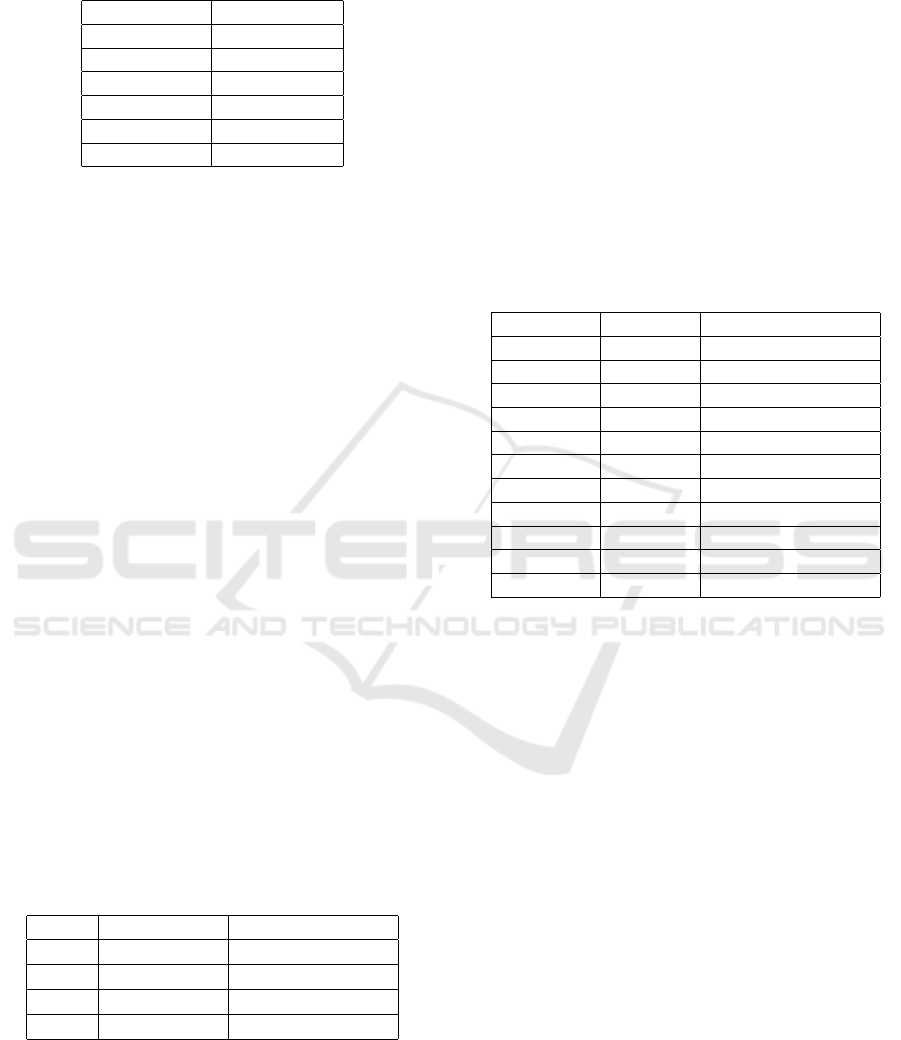
Table 4: Testing accuracy of the trained ANN models for

each LFSR. In the table, LFSRs are identiﬁed by their de-

gree.

LFSR degree Test accuracy

42 100%

46 100%

100 99.9%

155 100%

177 97.8%

250 99.2%

. While the results show that in the case of higher

LFSR degrees a dataset of size 10

is no longer sufﬁ-

cient, the increase in data is observed to be steady and

still under the threshold of (Kant et al., 2009). Thus,

the current study nuances that of (Boanc

a, 2024)(a) in

terms of clarifying how the training set size scales for

higher LFSR degrees.

The increase in the number of bits needed for gen-

erating the training set is motivated by the high de-

gree - low number of taps situation for LFSRs de-

gree ≥ 100 which leads to a disproportionately high

amount of 0 output labels. (Boanc

a, 2024)(a) based

its optimization on the sliding window approach on

contiguous bits (which, for the studied LFSRs degree

< 100 produced balanced output labels). For the LF-

SRs degree ≥ 100 in the current study the sliding win-

dow approach produces disproportionately more data

entries corresponding to label 0 than to label 1. Thus,

the increase in the number of bits stems from the need

of “gathering” sufﬁcient 1-labeled instances among

those labeled with 0 and discarded to create a bal-

anced training set (as ANNs are sensitive to statistical

bias).

Table 5 displays a comparison between the current

approach and that of (Kant et al., 2009) regarding the

magnitude degree of the size of the training set for

LFSRs degree ≥ 100.

Table 5: Comparison of the degree of magnitude between

the number of necessary training bits in the current ap-

proach as opposed to (Kant et al., 2009) for LFSRs degree

≥ 100.

LFSR Current work (Kant et al., 2009)

100 10

155 10

177 10

250 10

5.2 Geffe

5.2.1 Learning from Consecutive Seeds

The models trained on Geffe seeds to predict future

outputs prove the ability of ANNs to capture patterns

with (almost) perfect accuracy in the case of the Geffe

PRNG as well. The results are displayed in Table 6.

The obtained training time on a CPU is at most 3 sec-

onds per epoch, amounting to a total of less than 5

minutes for each Geffe conﬁguration.

Table 6: Results for learning from Geffe seeds. The Geffe

conﬁguration is presented as a the sequence of its consisting

LFSR degrees. The testing accuracy as well as the epoch

of convergence (i. e. the epoch in which both train and

validation accuracy reach 100%) are presented.

LFSR Accuracy Convergence epoch

19,42,53 100% 4/50

19,42,59 100% 17/50

19,46,53 100% 17/50

19,46,59 100% 15/50

19,53,59 100% 17/50

42,53,59 100% 17/50

46,53,59 100% 19/50

19,53,100 100% −/100

42,59,155 99.9% 41/50

46,53,177 99.6% −/100

53,59,250 100% 20/50

While the obtained results are accurate, efﬁcient

and successfully manage to reduce domain knowl-

edge when compared to the approach in (Boanc

2024)(a), we observe that the number of models to

be trained increases for every new Geffe conﬁgura-

tion. In (Boanc

a, 2024)(a) this issue is mitigated by

the use of a pipeline where each LFSR is learned

separately, then its corresponding model is only ag-

gregated when needed. Thus, no additional training

needs to be performed for novel Geffe conﬁgurations

which represent permutations of existing LFSRs. In

the case of our model, however, when LFSR permu-

tations happen inside the Geffe seed, an entirely new

model needs to be trained.

We attempt to use the fact that the current ap-

proach obtains highly accurate results (thus, we as-

sume it manages to robustly extract information) as

well as a model visualization component to derive an

optimization in this regard.

A weight visualization technique similar to that

in (Kim and Kim, 2021) is employed to observe the

strength of the connection between input features and

the neurons in the ﬁrst layer of the trained ANN.

Stronger connections denote higher importance asso-

ciated to certain features. Thus, it may be possible to

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

124

understand how the model learns from the data, using

the importance it gives to each bit of input. Figure 3

displays these results for a Geffe conﬁguration con-

sisting of LFSRs with degrees 19, 53 and 59.

Figure 3: Model visualization corresponding to a Geffe con-

ﬁguration described as 19,53, 59 by its LFSR degrees. Note

how bits at the ﬁnal position in each LFSR share stronger

connections to the input neurons.

Notably, higher importance is given to a set of 3

bits in the Geffe seed. Further investigation shows

that the highlighted values are the ﬁnal bits of each

LFSR in the Geffe seed. We attempt to capitalize

on this piece of knowledge to derive an optimiza-

tion for Geffe which uses a single model to make ac-

curate predictions for any conﬁguration. Since the

model gives higher importance to the ﬁnal bits of

each LFSR within the Geffe seed, we assume it is

enough to “ﬁt” any new conﬁguration on an already

trained Geffe model in the following manner: LFSRs

of higher degree are “ﬁt” in place of LFSRs of lower

degree through initial bits cropping; LFSRs of lower

degree are “ﬁt” in place of LFSRs of higher degree

through 0 initial padding. Figure 5 demonstrates these

approaches.

Figure 4: Fitting new LFSR seeds in an existing model.

Higher degree LFSRs undergo initial bits cropping. Lower

degree LFSRs undergo 0 initial padding.

The aforementioned optimization assumes that the

degrees of the LFSRs in the Geffe conﬁguration are

known. However, this assumption is the same as

in (Boanc

a, 2024)(a) and, thus, serves for compar-

ison purposes. Experiments are performed ﬁtting a

19,42,53 conﬁguration on the 46,53, 59 Geffe model

and the reverse and 100% accuracy is obtained for the

ﬁrst 100 generated bits in each case, thus deeming the

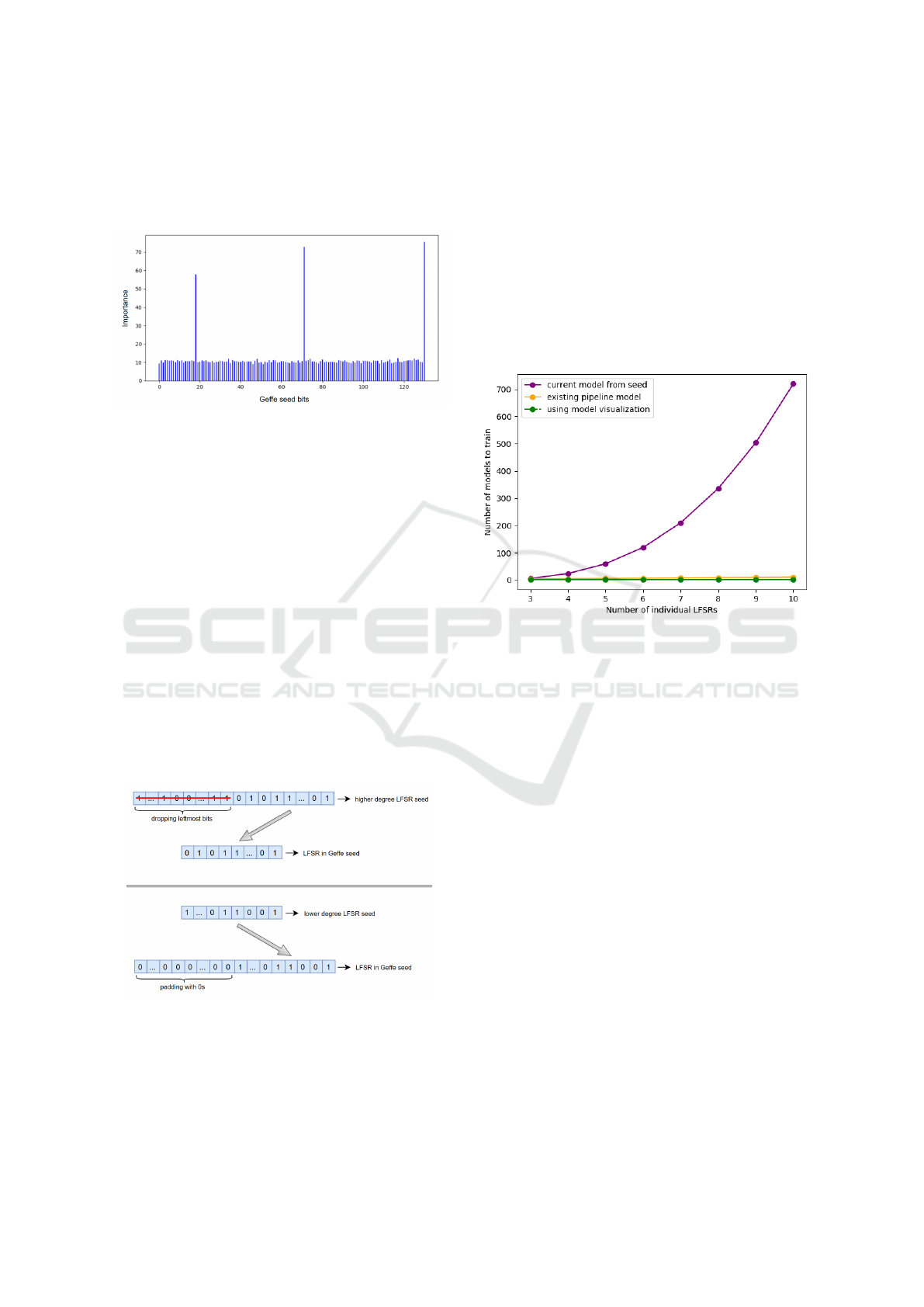
approach successful. A comparison between the num-

ber of models which need to undergo training in each

approach (the pipeline in (Boanc

a, 2024)(a), the cur-

rent Geffe seed learning approach and the proposed

optimization using model visualization) is displayed

in Figure 5 showing the superiority of the optimiza-

tion.

Figure 5: Comparison in terms of number of models needed

to be trained between the approach in (Boanc

a, 2024)(a),

the Geffe seed learning approach and the proposed opti-

mization using model visualization. The comparison covers

the case in which new LFSRs are added to form new Geffe

conﬁgurations.

5.2.2 Learning from Consecutive Outputs

While the model trained on Geffe outputs only man-

aged to increase its training accuracy, the validation

accuracy remained rather low or a ﬂuctuating pattern

occurred. We assume this may be due to the size of

the training set. Further increase was attempted, but it

became difﬁcult to process by the system RAM.

We believe, however, that more robust computa-

tional devices may be able to achieve better results.

6 DISCUSSION AND FUTURE

WORK

The present paper studies the manner in which cur-

rent state of the art approaches in terms of learning

from LFSRs with ANNs (Boanc

a, 2024)(a) scale for

LFSRs degree ≥ 100. It ﬁnds that the particular na-

ture of tap distribution on some of these LFSRs results

in an uneven distribution of patterns, thus accounting

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe

125

for the need to increase the number of training bits

to obtain a balanced number of samples for each pat-

tern. However, this increase is not dramatic and the

obtained models still outperform those in (Kant et al.,

2009) in terms of data efﬁciency.

Both the LFSR and the Geffe seed learning

models produce highly accurate results. In particular,

when the latter is coupled with a model visualization

component an optimization is derived for the number

of necessary models to be trained in case of Geffe

conﬁguration changes.

Perfect Learning vs. Overﬁtting. Both of the

proposed approaches (for LFSRs and Geffe) obtain

a high level of accuracy, sometimes even achieving

100%. This raises the pertinent question of whether it

is possible that the trained models simply overﬁt the

data. We desire to elaborate on this and for that, we

would like to return to what was discussed in Section

4.1, more precisely, the fact that for LFSRs only bits

at tap positions inﬂuence the output, while the others

are considered noise. The nature of PRNGs is de-

terministic, meaning that all inputs are processed in

the same way to obtain the outputs. This implies that

the same input will always result in the same output.

On the contrary, for other problems found in “nature”,

such as object classiﬁcation in images, the situations

that arise may be more nuanced and fuzzy: the same

object may be placed in different positions, under var-

ious lighting conditions, accounting for a virtually in-

ﬁnite set of arrangement possibilities. The problem

of overﬁtting the data refers to obtaining models that

learn exceedingly well on the training set, but are un-

able to generalize on new, unseen examples as they

lack the ability of correctly extracting distinguishing

features. This may be equivalent to performing im-

age classiﬁcation for objects such as mugs, with the

training set consisting only of blue colored mugs. It

is possible that the model incorrectly learns that in or-

der for an object to be classiﬁed as a mug, it needs to

have the color blue. Hence, the color of the mug is

incorrectly presumed a distinguishing feature. Need-

less to say, this will lead to the incorrect classiﬁcation

of mugs of other colors in the testing phase.

In the case of LFSRs it is essentially impossible

that a model trained on a sufﬁcient amount of data

overﬁts, since arrangement possibilities for distin-

guishing features are limited, 2

number o f taps

. It is vital

that various arrangements of noisy bits are present

in the training set in order to facilitate model distin-

guishing important information from noise. As such

a model is successfully trained, it is considered that

it understands which data features, or bits, are key to

producing the output and, having learned to assign

higher weights to each of them, will produce the same

results in the case of other learning examples that are

similar in terms of bit conﬁgurations at tap positions,

but differ only in the conﬁguration of noise. Thus, it

is not overﬁtting, but rather perfect learning that takes

place, due to the deterministic nature of PRNGs. To

account for that, various approaches in the literature

(Mostafa Hassan, 2021), (Kim and Kim, 2021) used

model understanding to observe weight values. It

resulted that bits at key positions are always those

that have the strongest ties to the network. We can

conﬁrm that this is the case for both our LFSR and

our Geffe models (for the latter, model visualization

is displayed in Figure 3). In case of Geffe, the most

important bits are those at the ﬁnal position in each

LFSR seed, as they will be combined using the Geffe

formula to derive the output.

Model Visualization. The model visualization com-

ponent is, thus, essential, and it may be used for

model understanding (checking it extracts meaningful

information) and, as we see in the current approach, it

may be exploited to derive optimizations. While cur-

rent learning perspectives for PRNGs approach prob-

lems with a black box mentality: simply input the data

to a learning model to derive the outputs, we mili-

tate for an increased use of visualization as the deter-

ministic nature of PRNGs allow for various optimiza-

tion possibilities (Mostafa Hassan, 2021), (Boanc

2024)(a). We believe that it is through approaching

PRNG learning problems in this manner that impor-

tant advances may be achieved.

Last but not least, we attempt to learn from a more

complex formulation of the Geffe problem, namely

learning directly from outputs. While unsuccessful,

the results were not discouraging, in the sense that

it is believed that advanced computational resources

may be able to perform the task given more data.

In the Context of IoT. Through these approaches we

observe the possibilities and limitations of learning

from LFSRs and their variations with ANNs. This is

of particular interest since IoT devices base their ran-

domness sources on similar PRNGs. We perform the

aforementioned incremental advances in order to con-

tribute to the possibility of creating fully intelligent

Machine Learning test suites to run on IoT devices.

Our assumption is as follows: it is believed that the

limit upon Machine Learning is not imposed by the

problems, but rather by the amount of data and com-

putational capacities. As the latter may be presumed

to enlarge in the future, one may successfully tackle

problems such as Geffe output learning, or even the

more complex stream cipher learning. However, upon

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

126

reaching this point it is essential to have well formed

learning approaches that are actually capable to ad-

dress the problem in a reliable manner. The current

incremental expansion on PRNG learning is proposed

to provide stepping stones such that robust security

evaluation may be provided for complex PRNGs in

the context of IoT in the future.

7 CONCLUSION

The present paper examines the manner in which ex-

isting literature approaches for ANN learning on LF-

SRs scale in the case of higher LFSR degrees. More-

over, it formulates a novel Geffe learning task to miti-

gate the excessive use of domain knowledge in previ-

ous approaches. While the results are highly accurate,

challenges are identiﬁed in terms of the number of

models that need to be trained for various Geffe con-

ﬁgurations. To address these challenges, the present

paper capitalizes on model visualization corroborated

with the ANN ability towards the perfect learning

of deterministic functions to derive an optimization.

A wide discussion ensues on the implications of the

aforementioned concepts for the problem of learning

from PRNGs and the solution is regarded in the con-

text of improving IoT evaluation of PRNG security by

means of neural networks.

REFERENCES

Amigo, G., Dong, L., and Ii, R. J. M. (2021). Forecast-

ing pseudo random numbers using deep learning. In

2021 15th International Conference on Signal Pro-

cessing and Communication Systems (ICSPCS), pages

1–7. IEEE.

Boanca, S. (2024). Exploring patterns and assessing the se-

curity of pseudorandom number generators with ma-

chine learning. In ICAART (3), pages 186–193.

Boanc

a, S. (2024). Optimizations for learning from linear

feedback shift register variations with artiﬁcial neural

networks. In IFIP International Conference on Artiﬁ-

cial Intelligence Applications and Innovations, pages

197–210. Springer.

Cui, L., Yang, S., Chen, F., Ming, Z., Lu, N., and Qin, J.

(2018). A survey on application of machine learning

for internet of things. International Journal of Ma-

chine Learning and Cybernetics, 9:1399–1417.

Feng, Y. and Hao, L. (2020). Testing randomness using

artiﬁcial neural network. IEEE Access, 8:163685–

163693.

Fischer, T. (2018). Testing cryptographically secure pseudo

random number generators with artiﬁcial neural net-

works. In 2018 17th IEEE International Confer-

ence On Trust, Security And Privacy In Computing

And Communications/12th IEEE International Con-

ference On Big Data Science And Engineering (Trust-

Com/BigDataSE), pages 1214–1223. IEEE.

Gohr, A. (2019). Improving attacks on round-reduced

speck32/64 using deep learning. In Advances in

Cryptology–CRYPTO 2019: 39th Annual Interna-

tional Cryptology Conference, Santa Barbara, CA,

USA, August 18–22, 2019, Proceedings, Part II 39,

pages 150–179. Springer.

Gupta, S., Singh, P., Shrotriya, N., and Baweja, T. (2021).

Lfsr next bit prediction through deep learning. Journal

of Informatics Electrical and Electronics Engineering

(JIEEE), 2(2):1–9.

Hussain, F., Hussain, R., Hassan, S. A., and Hossain, E.

(2020). Machine learning in iot security: Current so-

lutions and future challenges. IEEE Communications

Surveys & Tutorials, 22(3):1686–1721.

Ince, K. (2024). Exploring the potential of deep learning

and machine learning techniques for randomness anal-

ysis to enhance security on iot. International Journal

of Information Security, 23(2):1117–1130.

John Labelle (2020). Everyone Talks About Insecure Ran-

domness, But Nobody Does Anything About It. https:

//www.airza.net/2020/11/09/everyone-talks-about-i

nsecure-randomness-but-nobody-does-anything-abo

ut-it.html. Online; accessed 21 November 2022.

Kant, S. and Khan, S. S. (2006). Analyzing a class of

pseudo-random bit generator through inductive ma-

chine learning paradigm. Intelligent Data Analysis,

10(6):539–554.

Kant, S., Kumar, N., Gupta, S., Singhal, A., and Dhasmana,

R. (2009). Impact of machine learning algorithms

on analysis of stream ciphers. In 2009 Proceeding

of international conference on methods and models in

computer science (ICM2CS), pages 251–258. IEEE.

Kietzmann, P., Schmidt, T. C., and W

ahlisch, M. (2021). A

guideline on pseudorandom number generation (prng)

in the iot. ACM Computing Surveys (CSUR), 54(6):1–

38.

Kim, J. and Kim, H. (2021). Length of pseudorandom bi-

nary sequence required to train artiﬁcial neural net-

work without overﬁtting. IEEE Access, 9:125358–

125365.

L’Ecuyer, P. and Simard, R. (2007). Testu01: Ac li-

brary for empirical testing of random number gener-

ators. ACM Transactions on Mathematical Software

(TOMS), 33(4):1–40.

Li, C., Zhang, J., Sang, L., Gong, L., Wang, L., Wang,

A., and Wang, Y. (2020). Deep learning-based secu-

rity veriﬁcation for a random number generator using

white chaos. Entropy, 22(10):1134.

Lv, N., Chen, T., Zhu, S., Yang, J., Ma, Y., Jing, J., and Lin,

J. (2020). High-efﬁciency min-entropy estimation

based on neural network for random number genera-

tors. Security and Communication Networks, 2020:1–

18.

Massey, J. (1969). Shift-register synthesis and bch de-

coding. IEEE transactions on Information Theory,

15(1):122–127.

Pseudorandom Number Generators, Perfect Learning and Model Visualization with Neural Networks: Expanding on LFSRs and Geffe

127

Mostafa Hassan (2021). Cracking Random Number Gen-

erators using Machine Learning – Part 1: xorshift128.

https://research.nccgroup.com/2021/10/15/crackin

g-random-number-generators-using-machine-learnin

g-part-1-xorshift128/. Online; accessed 21 November

2022.

Noura, H., Couturier, R., Pham, C., and Chehab, A.

(2019). Lightweight stream cipher scheme for

resource-constrained iot devices. In 2019 Interna-

tional Conference on Wireless and Mobile Computing,

Networking and Communications (WiMob), pages 1–

8. IEEE.

Pasqualini, L. and Parton, M. (2020). Pseudo random num-

ber generation: A reinforcement learning approach.

Procedia Computer Science, 170:1122–1127.

Prashant Limba (2024). Predicting PRNG Sequence of

Subtractive Generator using Deep Learning. https:

//medium.com/@prashantlimba/predicting-prng-seq

uence-of-subtractive-generator-using-deep-learnin

g-4aa19f159dc4. Online; accessed 2 November 2024.

Robert G. Brown (2017). Dieharder, A Random Number

Test Suite. http://webhome.phy.duke.edu/

∼

rgb/Gener

al/dieharder.php. Online; accessed 4 October 2022.

Rukhin, A., Soto, J., Nechvatal, J., Smid, M., and Barker, E.

(2001). A statistical test suite for random and pseudo-

random number generators for cryptographic applica-

tions. Technical report, Booz-allen and hamilton inc

mclean va.

Savicky, P. and Robnik-

Sikonja, M. (2008). Learning ran-

dom numbers: A matlab anomaly. Applied Artiﬁcial

Intelligence, 22(3):254–265.

Schneier, B. (2007). Applied cryptography: protocols, al-

gorithms, and source code in C. john wiley & sons.

Truong, N. D., Haw, J. Y., Assad, S. M., Lam, P. K., and

Kavehei, O. (2018). Machine learning cryptanaly-

sis of a quantum random number generator. IEEE

Transactions on Information Forensics and Security,

14(2):403–414.

Zanin, M. (2022). Can deep learning distinguish chaos from

noise? numerical experiments and general considera-

tions. Communications in Nonlinear Science and Nu-

merical Simulation, 114:106708.

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

128