Curvy: A Parametric Cross-Section Based Surface Reconstruction

Aradhya N. Mathur

, Apoorv Khattar and Ojaswa Sharma

Indraprastha Institute of Information Technology Delhi, India

Keywords:

Graph Neural Networks, Parametric Representation, Shape Reconstruction.

Abstract:

In this work, we present a novel approach for reconstructing shape point clouds using planar sparse cross-

sections with the help of generative modeling. We present unique challenges pertaining to the representation

and reconstruction in this problem setting. Most methods in the classical literature lack the ability to gener-

alize based on object class and employ complex mathematical machinery to reconstruct reliable surfaces. We

present a simple learnable approach to generate a large number of points from a small number of input cross-

sections over a large dataset. We use a compact parametric polyline representation using adaptive splitting to

represent the cross-sections and perform learning using a Graph Neural Network to reconstruct the underlying

shape in an adaptive manner reducing the dependence on the number of cross-sections provided.

Project page: https://graphics-research-group.github.io/curvy/.

1 INTRODUCTION

Surface reconstruction from cross-sections is a well-

explored problem (Huang et al., 2017; Memari and

Boissonnat, 2008; Boissonnat and Memari, 2007; Ba-

jaj et al., 1996). There is a rich literature on methods

demonstrating the generation of reliable surfaces from

cross-sections for several applications. Medical imag-

ing and industrial manufacturing are some ﬁelds that

require reconstruction from such data. Little work ex-

ists that provides insights into how complex objects

could be generated using cross-sections with the help

of deep learning methods that could provide an added

advantage of capturing the semantic context associ-

ated with shapes. Deep learning-based methods (Sar-

mad et al., 2019; Park et al., 2019) can provide bet-

ter generalizability qualities associated with unseen

shapes of similar types by learning associated latent

representations. Several methods have extensively ex-

plored surface reconstruction from other inputs such

as point clouds (Brüel-Gabrielsson et al., 2020; Kazh-

dan et al., 2006; Peng et al., 2021). Inspired by these

two primary directions we aim to solve the task of

point cloud reconstruction from cross-sections unlike

the well-explored problem of surface generation from

incomplete point clouds. This brings unique chal-

lenges that we aim to address in this paper. Given the

proven effectiveness of deep learning in point cloud

https://orcid.org/0000-0001-6141-5849

https://orcid.org/0000-0002-9902-1367

generation, we leverage these methods to generate 3D

point clouds that can subsequently be used for surface

reconstruction, as extensively explored in prior work.

Thus, our focus is on the generation of high-quality

point clouds from sparse unorganized cross-sections.

Previous approaches for point cloud completion have

focused on generating point clouds from images or

representation learning using autoencoders. Several

previous methods focused on generating surfaces us-

ing cross-sections and did not involve any learning

based on the class of objects. Our method can be

used with any modern encoder-decoder-based point

cloud generation since it focuses on learning the latent

embeddings rather than generating the point cloud di-

rectly. Our approach introduces a novel input repre-

sentation for the cross-sections, aiming to capture cru-

cial information that would be overlooked when using

surface-sampled points. Point clouds, while dense in

most areas, often suffer from incomplete information

in certain regions. In contrast, cross-section curves

exhibit a highly non-uniform distribution of informa-

tion, necessitating reconstruction methods capable of

handling sparse and anisotropic data. By consider-

ing this unique characteristic of cross-sections, our

approach enables a more comprehensive and accurate

reconstruction of shapes. Our contributions can be

summarised as follows:

1. An approach for learning surface reconstruc-

tion based on parametric representation of cross-

sections for reconstruction,

Mathur, A. N., Khattar, A. and Sharma, O.

Curvy: A Parametric Cross-Section Based Surface Reconstruction.

DOI: 10.5220/0013300500003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 139-150

ISBN: 978-989-758-728-3; ISSN: 2184-4321

139

2. A novel framework for generating a point cloud

while adapting to the anisotropic and sparse na-

ture of input cross-sections. This constitutes two

attention mechanisms to focus on the local and

global structure of the cross-sections and show

their signiﬁcance empirically through an ablation

study, and

3. A new dataset for parametric representation of

cross-sections. The script for generating the

dataset shall be provided with the source code re-

lease.

2 RELATED WORK

Surface reconstruction is a widely studied problem in

computer graphics. As methods for representing 3D

data change, so do the methods for shape reconstruc-

tion. The different methods for representing 3D data

include a voxel-based representation that gives infor-

mation pertaining to points in a discrete grid, point

clouds that contain the locations of information, and

meshes that have added neighborhood information in

the form of an adjacency matrix corresponding to the

points. Newer implicit methods directly target surface

generation by learning to produce the implicit ﬁeld

functions. We divide this section based on the repre-

sentation of the output for different methods.

2.1 Pointcloud Generation

There are two primary approaches that have been ex-

plored for point cloud reconstruction. Reconstruc-

tion of point clouds has been done using multi-

view/single-view images and partial-point clouds.

A deep autoencoder network for the reconstruc-

tion of point clouds results in compact representations

and can perform semantic operations, interpolations,

and shape completion (Achlioptas et al., 2018),(Lin

et al., 2018). These networks leverage 1-D and 2-

D convolutional layers to extract latent representa-

tion for the generation of point clouds. Single im-

age point cloud generation has also been performed

hierarchically from low resolution by gradually up-

sampling the point cloud as explored in (Fan et al.,

2017). This multi-stage process uses EMD distance

(Fan et al., 2017) and computes Chamfer distance

for the later stages w.r.t. ground truth dense point

cloud. Another approach uses multi-resolution tree-

structured network that allows to process point clouds

for 3D shape understanding and generation (Gadelha

et al., 2018). Some newer methods also approach this

problem from a local supervision perspective to un-

derstand the local geometry better (Han et al., 2019).

Further, skip-attention has shown to play an impor-

tant role in tasks such as point cloud completion

(Wen et al., 2020). The architecture proposed con-

sists of primarily three parts - a point cloud encoder,

a decoder that generates the point cloud, and skip-

attention layers that fuse relevant features from the

encoder to the decoder at different resolutions. Rein-

forcement learning has also been explored with GANs

trained for the point cloud generation. The agent is

trained for predicting a good seed value for the ad-

versarial reconstruction of incomplete point clouds

(Sarmad et al., 2019). The method uses an autoen-

coder trained on complete point clouds to generate

the global feature vector (GFV) and a GAN that is

trained to produce GFV. The pipeline uses GFV gen-

erated from an incomplete point cloud as a state and

supplies it to an RL agent which the GAN uses to

generate GFV close to the GFV of a complete point

cloud.

2.2 Surface Reconstruction

One of the seminal works (Memari and Boisson-

nat, 2008) proposes constructing 2D geometric shapes

from 1D cross-sections. The method provides sam-

pling conditions to guarantee the correct topology

and closeness to the original shape for the Haus-

dorff distance. One of the early works (Huang

and Menq, 2002) proposes a manifold mesh recon-

struction method from unorganized points with arbi-

trary topology. The method proposed deﬁnes a two-

step process for reliably reconstructing the geometric

shape from unorganized point cloud sampled from its

surface.

Early works took inspiration from medical imag-

ing problems, a two-step process for the reconstruc-

tion of a surface from cross-sections has been pro-

posed by ﬁrst computing the arrangement for the

cross-section within each cell and then reconstruct-

ing an approximation of the object from its intersec-

tion with the cell boundary and gluing the pieces back

together yields to surface (Boissonnat and Memari,

2007). An algorithm for non-parallel cross-sections

consisting of curve networks of arbitrary shape and

topology has also been developed (Liu et al., 2008).

Several methods propose implicit ﬁeld-based recon-

struction. One such method utilizes sign agnostic

learning for geometric shapes (Atzmon and Lipman,

2020). This method uses a deep learning-based ap-

proach that allows learning of implicit shape repre-

sentations directly from unsigned raw data like point

clouds and triangle soups. The proposed unsigned

distance loss family possesses plane reproduction

property based on suitable initialization of the net-

work weights.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

140

The surface reconstruction method has been per-

formed with topological constraints (Lazar et al.,

2018). The method relies on computing candidates

for cell partitioning of ambient volume. The method

is based on the calculation of a single surface patch

per cell so that the connected manifold surface of

some topology is obtained. 3D surface reconstruc-

tion from unorganized planar cross-sections using a

split-merge approach using Hermite mean-value in-

terpolation for triangular meshes has also been used

(Sharma and Agarwal, 2017). A divide-and-conquer

optimization-based strategy can also be employed

to perform topology-constrained reconstruction (Zou

et al., 2015). New methods like Orex (Sawdayee

et al., 2022) leverage deep learning for cross-section

to surface generation.

3 APPROACH

In this work, we develop an approach for shape re-

construction from a set of unorganized cross-sections.

We design a deep neural network that learns the over-

all structure of various shapes and generates a point

cloud representing the original object. Our approach

can be deﬁned as a three-step process. We ﬁrst gener-

ate a large number of cross-sections from 3D models

and sample them to create input cross-sectional data.

Then surface points are sampled to generate a point

cloud on which an autoencoder is trained to recon-

struct the point cloud. In the ﬁnal step, we use the en-

coded vector obtained from the autoencoder and train

a Graph Neural Network on the parametric represen-

tation of input cross-sections to generate an embed-

ding vector in a GAN-based setting to match the en-

coded vector for the same object. These embedding

vectors are then decoded to get a point cloud from the

pre-trained autoencoder network.

Cross-section-based reconstruction has applica-

tions in several domains such as the manufacturing

of 3D components and 3D printing using CAD mod-

eling, and the medical domain where 2D ultrasound

slices are captured in 3D. Instead of sampling points

from the cross-sections, we convert an entire cross-

section curve into its parametric representation which

is a more versatile representation as it allows us to

reduce any loss of information that may occur due

to sampling and further helps reduce the memory re-

quirements needed to represent a large number of

points in the neural network, thus helping to capture

complex curves using fewer parameters. Let us as-

sume the density of points ρ per unit length of a cross-

section curve of length l. Depending on the sampling

density ρ, the number of points in a curve can vary,

and for better information capture we need a high ρ

value to capture the curvature accurately. We note that

the parametric curve can be represented using a ﬁxed

number of coefﬁcients from which any arbitrary den-

sity of points can be sampled. Our overall approach

is shown in Figure 1.

3.1 Adaptive Splitting

It is important to ensure that a simpler piece (such

as a straight line) is represented by fewer points so

that more points can be assigned to a piece with

many sharp turns. We propose an adaptive splitting

scheme for non-uniform distribution between pieces

using the Douglas-Peucker polyline simpliﬁcation al-

gorithm (Douglas and Peucker, 1973) for ﬁnding a set

of endpoints to generate the pieces within the curve.

This helps to save more points for complex curves and

uses fewer points for simpler curves further retain-

ing more information than a uniform splitting scheme.

Douglas-Peucker algorithm is run for multiple iter-

ations till the ﬁnal number of unique endpoints re-

turned is more than k, we select the k points with max-

imum absolute angle, where the angle varies between

−90 and +90. Each cross-section is divided into k

pieces using an adaptive splitting scheme. For the j

piece with n

points, we obtain the parameter values

of the parametric function using the Chordal approxi-

mation (Floater and Surazhsky, 2006) as,

i, j

= t

i−1, j

||p

i, j

− p

i−1, j

∑

i=2

||p

i, j

− p

i−1, j

where p

for i ∈ 1, 2, ...n

are points on a piece, and

= 0 such that for each piece t

∈ [0, 1]. Once we

have obtained k pieces, we ﬁt piece-wise polynomi-

als by solving the KKT conditions (Kuhn and Tucker,

2014) by formulating a least squares problem (Boyd

and Vandenberghe, 2018).

3.2 Training on Parametric Space

We take the ShapeNet dataset (Chang et al., 2015) and

use the manifold meshes. The input cross-sections

are generated using mesh-plane intersection and con-

verted to parametric representation. Further in the

text, cross-sections shall refer to the parametric repre-

sentation of cross-sections. We sample surface points

from the meshes; thus, each set of cross-sections and

the corresponding point clouds form the input and the

corresponding ground truth for the network. In order

to use parameters with a neural network there are cer-

tain properties that the operations on the parametric

Curvy: A Parametric Cross-Section Based Surface Reconstruction

141

Input cross-sections

Piece-level graph

Graph

convolutions

Graph

convolutions

Point cloud

decoder

Generated point cloud

Figure 1: Overview of our reconstruction approach. Starting from a parametric representation of the given cross-sections, we

train a network to generate a surface point cloud.

representation must possess. Each piece of a cross-

section is represented as a tensor in R

6×3

of coefﬁ-

cients of the parametric representation f

(t) of degree

5 in R

. See Figure 2 for our parametric curve repre-

sentation and its corresponding graph.

(t)

[θ

0, j

, · · · , θ

p, j

]

Piecewise curve Piece-level graph

Figure 2: Converting a piecewise parametric representation

of a cross-section (left) to a graph (right). The nodes in the

graph are matrices of coefﬁcients of the parametric func-

tions.

3.2.1 Permutation Invariance and

Neighborhoods

We represent the coefﬁcients of the parametric rep-

resentation as a vector for the neural network to act

on. Thus, the cross-sections are represented as ten-

sors containing the vector for each parametric piece.

Further, the cross-sections contain neighborhood in-

formation in the form of adjacency of the pieces.

Therefore, the operations that we perform on the

cross-sections must be permutation invariant since

any combination of cross-sections represents the

same object. Given a set of m parameterized cross-

sections where each cross-section is partitioned into k

pieces with the coefﬁcient matrix Θ

of the paramet-

ric functions for the l

piece, the full set of stacked

coefﬁcients for the entire set of cross-sections are rep-

resented as the tensor C =



, Θ

, ··· , Θ



⊺

of size

m × (p + 1)k × 3. Any permutation of rows of C still

represents the same set of cross-sections (that is to

say that the cross-sections can come in any order)

and any circular permutation of these pieces repre-

sents the same cross-section. Therefore, any opera-

tion performed on C should ideally yield the same re-

sult irrespective of the ordering of its rows and any

circular permutation within each row. Within a neu-

ral network, representations are created using matrix

multiplications, and different orders of the rows and

columns of C would produce different results since,

⊺

C ̸= W

⊺

′

(C ),

where W is a weight matrix and S

′

is a shufﬂe opera-

tion. Therefore we do away with this matrix-based

representation. We create a graph-based represen-

tation using the piecewise parametric representation.

We note that each cross-section has some adjacency

information since the pieces of a cross-section are ar-

ranged in linear order along the contour. In order to

use the neighborhood properties, we propose a graph-

based representation, where each node is represented

as the matrix of coefﬁcients of a piece of the para-

metric curve and each edge denotes the adjacency.

The graph-based representation allows our approach

to take into account the desired permutation invari-

ance while enabling us to use the additional adjacency

information as needed. Therefore, our ﬁnal represen-

tation uses coefﬁcients of the pieces where the adja-

cency matrix stores the piece-level relations.

3.2.2 Learning Point Cloud Representation

We train a point cloud auto-encoder on the ground

truth point cloud generated by sampling 2048 points

from the manifold meshes and then use the encoder

embedding from this as the ground truth embedding

similar to the method presented in RL-GAN-Net (Sar-

mad et al., 2019), whereby a GAN is used to generate

an embedding similar to that of a pre-trained point

cloud auto-encoder which is very stable for training

while allowing for stochasticity. Thus, the objective

of the graph encoder is to learn the embedding from

the cross-sections to produce a similar point cloud

from the pre-trained decoder, as shown in Figure 3.

3.2.3 Cross-Section Attention

Attention mechanism (Vaswani et al., 2017) allows a

network to focus on different features and enables bet-

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

142

Figure 3: During training, the graph embedding decoder

tries to generate an embedding that is similar to the point

cloud embedding generated from the pre-trained encoder.

This representation is then used by the decoder to generate

the point cloud of a relevant shape.

ter learning of the network. Taking inspiration from

this, we introduce attention at two levels in our net-

work for learning shapes. We use two levels of cross-

section attention mechanism, which we call global at-

tention, and a piece-wise attention mechanism for fo-

cusing on local information. Each cross-section con-

tains different amounts of information pertaining to

the geometric shape of the object. Similarly, within

a cross-section, some pieces contain more informa-

tion pertaining to the local regions, such as regions

of high curvature. In order to focus on such regions,

we introduce local attention, which attends to each

piece within a cross-section. The global and local at-

tention are computed using Graph Attention (Velick-

ovic et al., 2018). The normalized attention coefﬁ-

cient at the graph level can be expressed as α

i, j

so f tmax(e

i, j

) where α

i, j

are the normalized attention

coefﬁcients for node i in the graph, j ∈ N

where N

is the neighbourhood of node i and e

i, j

is the attention

coefﬁcient. The attention coefﬁcient is calculated us-

ing the same method as described in (Velickovic et al.,

2018).

First, attention is computed locally over the pieces

of each cross-section, which we then aggregate into

a single vector to represent each cross-section node.

Finally, we apply the cross-section level attention for

which we create a new adjacency matrix represent-

ing a complete graph. Since, at the cross-section

level, there is no strict adjacency, representations for

each cross-section must be learnable. We let the net-

work perform attention on the complete graph giving

it complete ﬂexibility to attend to any cross-section.

We still need to maintain the graph-level representa-

tion at this stage since we still require permutation

invariance at this stage.

In our implementation, in order to restrict the at-

tention to piece-level and cross-section levels, we ex-

plicitly pass the piece-level adjacency matrix during

initial graph convolutions; this restricts the neighbor-

hood of the nodes to attend within cross-sections, af-

ter which we aggregate the piece-level information

and later replace the adjacency matrix with a com-

plete graph adjacency.

3.2.4 Adapting for Variable Cross-Sections

Since the network takes the input in the form of para-

metric cross-sections, where each cross-section con-

sists of piecewise C

parametric curves, the param-

eters of the network become ﬁxed during training if

MLPs are used, prohibiting any changes in the num-

ber of cross-sections or pieces provided. In order to

adapt to the variable nature of our data, we are fur-

ther motivated to use the graph-based representation

by allowing piece-level aggregation and cross-section

level aggregation, which allows for a variable num-

ber of cross-sections to be provided to the network.

Furthermore, we cannot use 1-D-convolutions or 2-

D convolutions directly in the parametric space be-

cause convolutions are not well deﬁned on coefﬁcient

spaces.

We use graph convolutions in both the genera-

tor and discriminator. The discriminator is condi-

tioned using the input graph parameters and predicts

whether the generated embedding vector is real or

fake, the input graph is converted to a graph-level

embedding using successive graph convolutions (Kipf

and Welling, 2017) and aggregation. Then the embed-

ding vector is concatenated with the generated em-

bedding and passed to subsequent layers. While the

generator consisted of SAGEConv (Hamilton et al.,

2017) followed by DiffNorm (Zhou et al., 2020) to

prevent over-smoothing and allow for deeper network

and Graph Attention Convolutions (Velickovic et al.,

2018) followed by aggregation and fully connected

layers to generate graph embedding. In order to allow

for stochasticity in the generated outputs like in a gen-

eral GAN setting, we append a noise to the parameter

vector of each piece.

3.2.5 Training Details

Given a pre-trained autoencoder with encoder En and

decoder De and a GCN-based generator-discriminator

Curvy: A Parametric Cross-Section Based Surface Reconstruction

143

Aircraft Chair Sofa

Ground Truth Predicted Ground Truth Predicted Ground Truth Predicted

10 cross-sections5 cross-sections2 cross-sections

Figure 4: (Left) Comparison of reconstruction quality with an increasing number of cross-sections. Input to the network is

the set of cross-sections (red) belonging to the ground truth mesh (blue).

pair {G, D} we pass a ground truth point cloud P

containing 2048 points through the encoder to gener-

ate an embedding, En(P

). For a set of input parame-

terized cross-sections C, we create the piece-wise ad-

jacency matrix A

for each cross-section and a cross-

section adjacency matrix A

The generator is trained to generate an embedding

using the cross-section set C and the two adjacency

matrices for the point cloud. The generator loss is

given by

=log(1 − D (G (C, A

, A

),C, A

, A

))+

(De(G(C, A

, A

)), De(En (P

)))+

mse

(G(C, A

, A

), En (P

)),

where L

is the Chamfer loss between the point

clouds generated using the embedding estimated by

the generator and the embedding of the ground truth

point cloud. L

mse

is the mean squared error between

the embedding estimated by the generator and the em-

bedding of the ground truth point cloud. The discrim-

inator loss can be formulated as

=(1 − log (D (G (C, A

, A

),C, A

, A

)))+

log(D(En (P

),C, A

, A

)),

where the discriminator is conditioned on the input

cross-section graph. The generator and discriminator

are trained in an adversarial manner (see (Goodfellow

et al., 2020)).

4 RESULTS AND DISCUSSION

We evaluate our approach on different classes of the

ShapeNet dataset. We perform an experimental pro-

cedure similar to DeepSDF where we divide the mod-

els into known shapes, i.e. shapes that were in the

training set and testing set referred to as unknown

shapes. We test our method in both single-class and

multi-class settings.

We show some samples for single-class training as

well in Figure 5. However, our key focus is on multi-

class training and its analysis is covered further.

Ground Truth with GCN output

cross-sections

Aircraft

Lamp

Figure 5: Results of the proposed model trained only on a

single class of objects. Input to the network are the cross-

sections (red) belonging to the ground truth mesh (blue).

We perform the training in a multi-class setting.

For the multiclass setting, we test on 4 classes - air-

plane (4K models), chair (6K models), lamp (2K

models), and sofa (3K models). Our implementation

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

144

Table 1: Per-class Chamfer distance corresponding to varia-

tion in the number of cross-sections. Results for both under-

sampled and oversampled (> 10) cross-sections are shown

for a model trained on all aforementioned classes.

# cross- Per-class Chamfer distance Mean

sections Airplane Chair Lamp Sofa

2 0.4050 0.1765 2.7306 0.3770 0.9223

5 0.0493 0.0872 0.2394 0.0772 0.1133

10 0.0395 0.0829 0.0958 0.0728 0.0728

11 0.0385 0.0824 0.0927 0.0724 0.0715

15 0.0378 0.0813 0.0909 0.0715 0.0704

20 0.0374 0.0807 0.0898 0.0709 0.0697

25 0.0370 0.0803 0.0896 0.0704 0.0693

source code has been made available on Github. We

do not perform any class balancing techniques and

directly train on the ShapeNet dataset. We use py-

torch geometric (Fey and Lenssen, 2019) for this. We

demonstrate the impact of these attentions via an ab-

lative study in Table 2. We test inference time on

NVIDIA GTX 1070. The model takes ∼0.19 sec. for

generating point clouds from 10 cross-sections.

4.1 Cross-Section Dependence

We compare the mean Chamfer loss obtained across

the different classes for different numbers of input

cross-sections (5, 10, 11, 15, 20, and 25) provided

as input in Table 1. We observe results for the Cham-

fer distance obtained after training are shown in Table

1. We observe that the number of cross-sections pro-

vided as input has a vital control on the output of the

generated point cloud surface, as can be seen from

Table 1. We show the results of the proposed model

trained on four classes: Airplane, Chair, Lamp, and

Sofa with a different number of input parameterized

cross-sections in Figure 4. The even column displays

the ground truth mesh used to sample the ground truth

point cloud with cross-sections, and the odd column

shows the reconstruction with our method.

We discuss these trends and perform the t-SNE of

the embeddings and demonstrate how the distinguish-

ing capabilities of the network improve further with

increasing the number of cross-sections. Further, in

Figure 4, we show that despite the sharp reduction

in the number of cross-sections, the network still gen-

erates a reliable general shape for the class and can

distinguish between the classes of parametric forms.

4.2 Impact of Adjacency

We show the impact of different kinds of attention

mechanisms and study the empirical changes in Ta-

ble 2. Firstly, we use ring adjacency strictly for the

nodes, and secondly, we change the adjacency at the

higher levels. This is done with the intuition that the

network should be able to view all the nodes during

attention operation since nodes that are similar would

share similar embeddings at higher levels given that

they share similar local neighborhoods. Thirdly, we

provide a complete graph adjacency throughout all

the levels and allow the network to deduce the re-

lationships itself. In Table 2 summarizes the results

for different connectivity information that is fed to the

network. We observe that despite providing the exact

neighbor information in the form of ring adjacency,

the network performs best for a complete graph adja-

cency; we suspect that this is due to better information

capture since each neighbor of a node is no longer re-

stricted to the adjacent nodes in the cross-section but

can also accumulate information from nodes that are

not directly linked allowing the network to get a better

information gain thus reducing the impact of informa-

tion bottleneck that graph neural networks suffer from

as the depth of network increases.

Table 2: Impact of different Adjacency-based attentions.

Approach Chamfer Loss (mean)

Change in loss with different attention strategies

Attention Cross-section level only 0.33693247

Attention Piece level only 1.10052492

Without Attention 9.02284977

Change in loss with different connectivity

Complete Graph from ﬁrst layer 0.86106642

Complete Graph at attention layers 5.80743287

Maintaining Ring Adjacency 9.57172529

4.3 Comparisons

This is a non-trivial task for many reconstruction

methods, as they often struggle to generate missing

structures from limited cross-sectional information.

Consequently, our approach holds practical value, as

it excels in accurately capturing the shape of objects

in scenarios where cross-section data is sparse.

We compare our method against 4 methods:

VIPSS (Huang et al., 2019) method for variational

surface reconstruction from cross-sections, surface

reconstruction from non-parallel curve networks (Liu

et al., 2008), a state of the art deep learning based

method P2P-Net (Yin et al., 2018) and the recent

OReX (Sawdayee et al., 2022) and show results in

Figure 6. Most of these methods suffer from holes

and instabilities for sparse cross-sections; therefore,

to be fair, we sample more cross-sections in those

cases. However, we restrict our method to 10 cross-

sections. VIPSS, OReX, and Liu’s method require

careful sampling and sometimes tend to fail randomly

for sparse cross-sections. We show the best-case re-

sults for these methods. VIPSS is very sensitive to λ

Curvy: A Parametric Cross-Section Based Surface Reconstruction

145

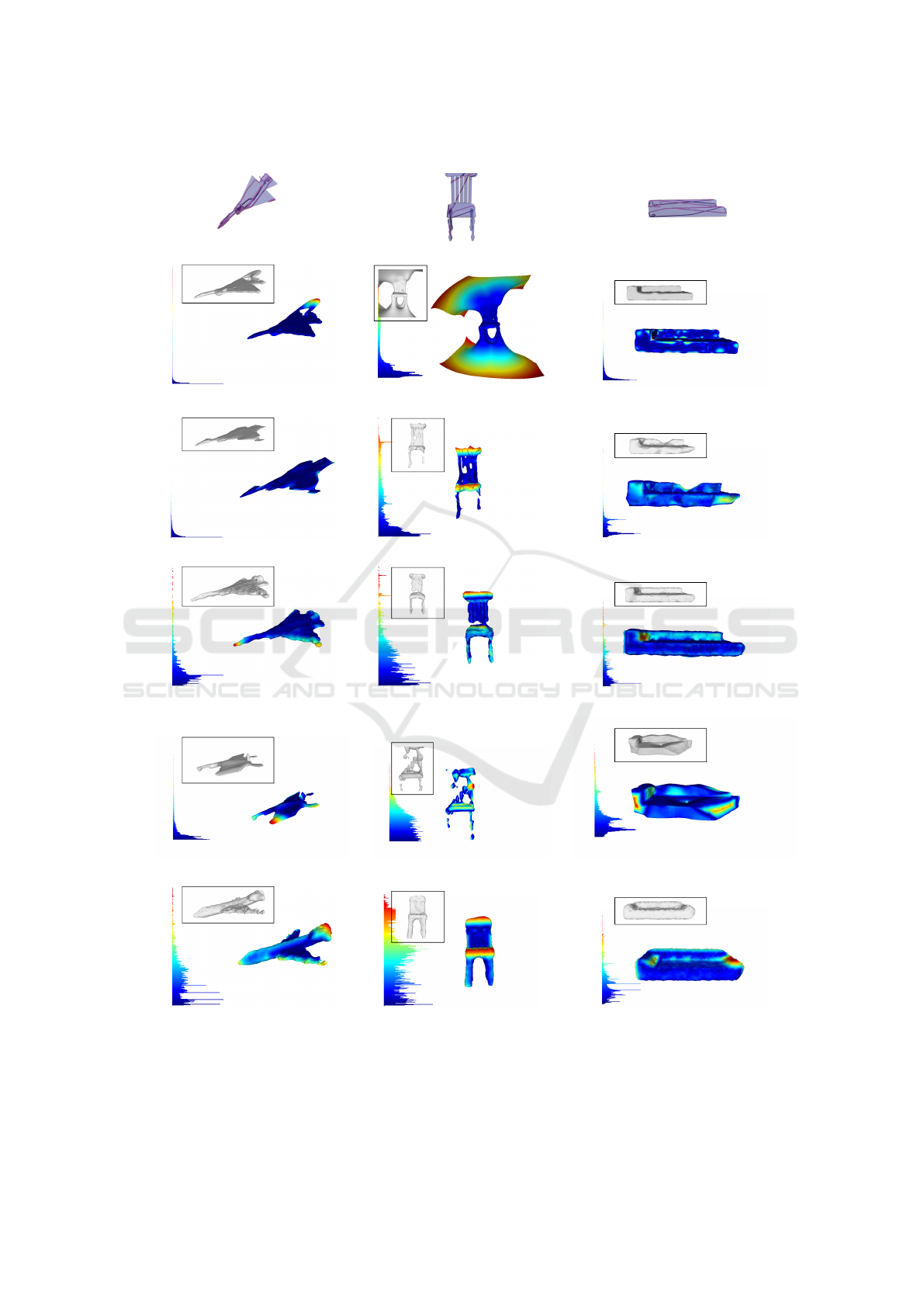
GT Mesh + Input

VIPSS (Huang et al., 2019)

: 0.032574 d

: 0.056161 d

: 0.001533

Liu et. al (Liu et al., 2008)

: 0.005765 d

: 0.039835 d

: 0.010035

P2P Net (Yin et al., 2018)

: 0.023185 d

: 0.032854 d

: 0.012473

OReX (Sawdayee et al., 2022)

: 0.022027 d

: 0.049031 d

: 0.015033

Ours

: 0.032111 d

: 0.049031 d

: 0.019826

Figure 6: Comparison with the state-of-the-art methods. The inset shows point-wise surface error compared with the GT. The

blue regions indicate areas of low error while brighter areas indicate higher error.

and requires a large number ∼ 80 of cross-sections for

faithful reconstruction due to failure due to openness

in cross-sections; however, we still notice artifacts.

We checked the reconstruction with the method

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

146

0.2

0.4

Number of cross-sections

0.05

0.1

Number of cross-sections

Aircraft Chair

Lamp

Sofa

−3

−2

−1

Number of cross-sections

−∆L

(a) (b) (c)

Figure 7: Dependence of Chamfer loss L

on the number of cross-sections. (a) Undersampling conditions, (b) Oversampling

conditions, (c) Negative change in mean Chamfer loss (log-scale).

proposed in (Liu et al., 2008), however, the avail-

able implementation discards many cross-sections

that lead to incorrect results. We show results for

the cases where we did not observe this issue for a

fair comparison. For OReX (Sawdayee et al., 2022)

as well, we observe that it performs really well when

cross-sections are dense; however, it fails in the case

of sparse cross-sections. Therefore, for some sam-

ples, we show results in cases where it performs rea-

sonably well.

We further compare our method against a state-of-

the-art deep learning-based method called P2P-Net.

We modify P2P Net and train it on points sampled

from our cross-sections. We notice that in some cases,

despite performing better in terms of metrics, there

are still completion issues in several samples, such as

the chair shown in Figure 6. Our method generates

symmetric structures leading to higher loss value but

better perception quality and semantically correct dif-

ferent structures such as the right-hand rest of the sofa

and missing leg in the chair. This also highlights a

weakness of our method pertaining to the lack of strict

adherence to the cross-sections since our method re-

lies on embedding decoded by the pre-trained de-

coder. However, we believe that can be circumvented

by better pre-training schemes since the performance

of the pre-trained decoder forms the lower bound of

the reconstruction error and can be swapped with any

of the better-performing point cloud generators.

In order to visualize the error in reconstruction

from our method and P2P-Net, we perform surface

meshing of our resulting point cloud with Poisson Re-

construction (Kazhdan et al., 2006) , by computing

normals from the ground truth mesh for the best-case

scenario. For VIPSS, we also modiﬁed the method

and provided normals from the GT mesh. We show

similar histograms for the surfaces obtained from

other methods. We also note the Hausdorff distance

) obtained for different methods in Figure 6. We

notice that during the generation of the point cloud

since our method does not have hard constraints for

precise overlap with input, the shift in point cloud can

lead to a relative rise in the Hausdorff distance, as can

be seen in the case of the chair in Figure 6. However,

it outperforms the other methods in both qualitative

and quantitative comparisons in several cases.

4.4 Changes in Embedding

Since the graph embedding also varies as the num-

ber of cross-sections changes, we try to reason how

the class information of embedding varies as we in-

crease the number of cross-sections. In order to do

so, we compute the t-SNE (Van der Maaten and Hin-

ton, 2008) from the embedding vectors of 200 sam-

ples of each class in the multi-class setting and plot

them to see how the cluster distance varies with cross-

sections. From Figure 8 we observe that in the under-

sampling conditions the overlap between the clusters

increases, thus making it difﬁcult for the network to

implicitly predict the class of the object, whereas as

the number of cross-sections is increased, the overlap

of clusters reduces. However, we also note that some

shapes exhibit a well-separated cluster even when the

number of cross-sections is less such as airplane in

this case. We also note that classes chair (denoted by

green) and sofa (denoted by grey), since these classes

are similar in shape, show weaker disentanglement in

the embedding space of cross-sections.

4.5 Loss Trends

In Figure 7(a) we see the case for undersampling,

as expected we observe that as the number of cross-

sections are reduced the amount of information sup-

plied to the network reduces, and hence the recon-

struction quality degrades. We also note that there is

a sharp dip in Chamfer loss when the cross-sections

are increased to 5, which is the minimum number

of cross-sections on which the network is trained.

Increasing the number of cross-sections to 10 im-

proves the reconstruction quality visually; however,

the changes in empirical values are not particularly

signiﬁcant, with most variations occurring on the or-

Curvy: A Parametric Cross-Section Based Surface Reconstruction

147

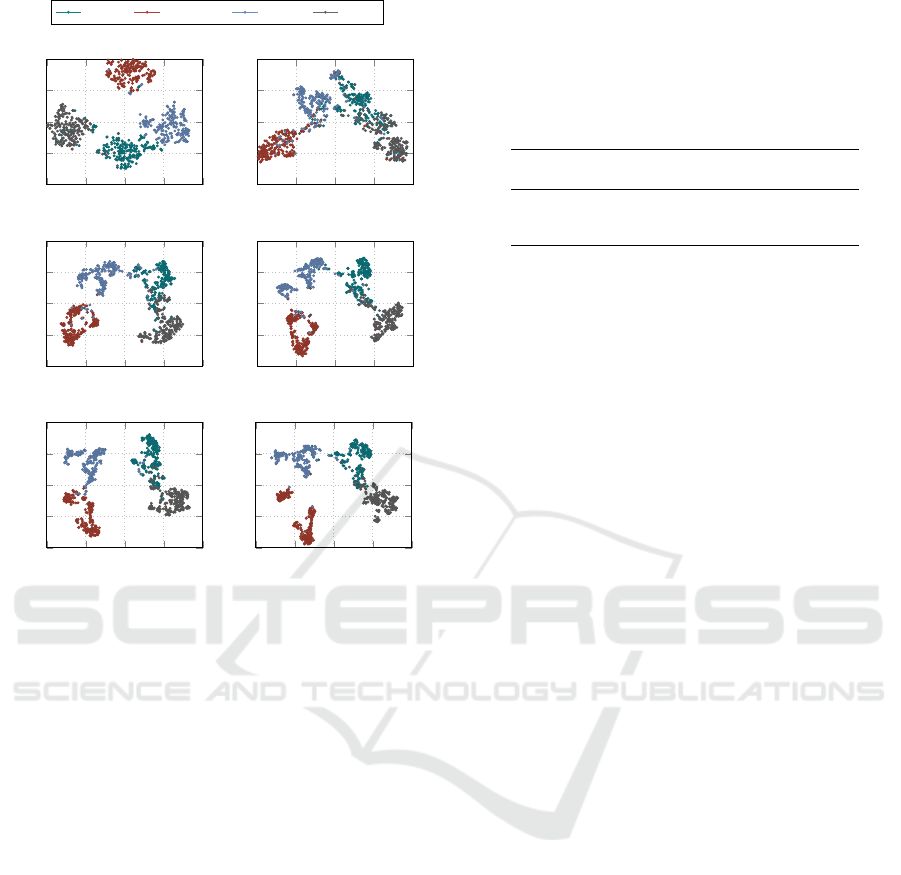
Chair Airplane

Lamp

Sofa

−40 −20 0 20 40

−40

−20

GT Embedding t-SNE

−40 −20 0 20 40

−40

−20

2 cross-sections

−40 −20 0 20 40

−40

−20

5 cross-sections

−40 −20 0 20 40

−40

−20

8 cross-sections

−40 −20 0 20 40

−40

−20

10 cross-sections

−40 −20 0 20 40

−40

−20

20 cross-sections

Figure 8: Changes in the t-SNE embedding clusters with

respect to the number of cross-sections.

der of 1e-3. This is evident in Figure 7(c), which de-

picts the case for oversampling when the number of

cross-sections is increased in the range of 15–25. In

the oversampling scenario, as shown in Figure 7(b),

a pronounced decline in the Chamfer distance is ob-

served up to 15 cross-sections. Beyond this point, fur-

ther increases in the number of cross-sections result in

minimal changes to the Chamfer distance. Nonethe-

less, the Chamfer distance continues to decrease grad-

ually as more information is provided to the network.

4.6 Variance in Loss

Further in Table 3, we show the standard deviations

for the losses across 20 different objects for vary-

ing cross-sections. We sample n ∈ {2, 5, 10} cross-

sections, randomly from the 100 cross-sections gen-

erated from the mesh as in our original experiment

setup and repeat this 40 times thus obtaining 40 ran-

dom samples for each object for a given n. We do this

to measure the standard deviation for the losses com-

puted for varying sampling of cross-sections. We ﬁrst

compute the standard deviation obtained across dif-

ferent samples for the same object for a given value of

n. Then we compute the mean over the standard devi-

ations obtained across different objects for the given

n. This helps us to understand further the variations

for loss across cross-sections for each object.

Table 3: In the above table we demonstrate a similar trend of

reducing standard deviation in the chamfer losses obtained

for varying cross-sections for 20 different objects sampled

40 times each.

No. Airplane Lamp Sofa Chair

of cross-sections

2 0.09262 0.6465 0.0634 0.1131

5 0.01925 0.1060 0.0165 0.0243

10 0.00675 0.0253 0.0105 0.00985

We observe in Table 3 that similar to the reduction

in mean Chamfer Losses in Table 1 in the paper, the

standard deviations vary across classes and across the

number of cross-sections. If the mean for a particular

class is low so is the variance in the loss since the

model is able to faithfully reconstruct the shape given

any given set of cross-sections. Further, as the cross-

sections increase the amount of information provided

to the network increases thus the standard deviations

reduce across the same object sampled multiple times.

4.7 Failure Cases

This is a non-trivial task for many reconstruction

methods, as they often struggle to generate missing

structures from limited cross-sectional information.

In some cases, the failure of reconstruction is much

higher depending on the number of samples of a par-

ticular shape of the object the network sees and the

information in the cross-sections supplied. For ex-

ample, in Figure 10, in an airplane object, the cross-

sections do not contain sufﬁcient information, leading

to a completely different object being created, though

it must be noted that the class of the reconstructed ob-

ject reconstructed is correct. We observe that in the

case of a failure, the network reconstructs a coarse

object of the correct class.

Further, we also notice a deterioration in the sam-

ples containing holes, such as chairs and lamps. For

example, in the case of the chair, the reconstruction

does not accurately maintain the genus of the object

for some samples.

5 CONCLUSION AND FUTURE

SCOPE

With this work, we open a new direction for the ex-

citing domain of cross-section-based reconstruction.

We generate a new dataset that can be used for multi-

ple tasks. The ability to use parametric cross-sections

directly in a learning-based setting exempts the use

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

148

Figure 9: In above ﬁgure who show additional results consisting of the cross-sections (pink) and the corresponding point

clouds generated.

Ground Truth Predicted

Figure 10: Failure cases resulting in incorrect shapes. Input

to the network are cross-sections (red) belonging to the GT

mesh (white).

of any sampling-based restrictions in deep learning-

based methods. The complete information of the

curve is encapsulated in the coefﬁcients of the para-

metric representation. Further, we utilize GCNs at

scale and demonstrate their effectiveness for para-

metric curves and the ability of the GCNs to capture

neighborhood information, which helps deduce bet-

ter relationships among the cross-sections using atten-

tion, adding to the explainability with the ﬂexibility to

use any models trained on point cloud generation. We

show empirical evidence to analyze the changes in re-

construction, both in terms of the embedding space

representation and point cloud reconstruction, to un-

derstand the changes with respect to the variation in

the amount of information provided to the network.

This builds a strong motivation and opens up the ﬁeld

to further research such as the disentanglement of la-

tent features and information-theoretic and in-depth

analysis of the cross-sections themselves which we

hope to cover in future works.

REFERENCES

Achlioptas, P., Diamanti, O., Mitliagkas, I., and Guibas, L.

(2018). Learning representations and generative mod-

els for 3D point clouds. In International conference

on machine learning, pages 40–49. PMLR.

Atzmon, M. and Lipman, Y. (2020). Sal: Sign agnostic

learning of shapes from raw data. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 2565–2574.

Bajaj, C. L., Coyle, E. J., and Lin, K.-N. (1996). Arbi-

trary topology shape reconstruction from planar cross

sections. Graphical models and image processing,

58(6):524–543.

Boissonnat, J.-D. and Memari, P. (2007). Shape reconstruc-

tion from unorganized cross-sections. In Symposium

on geometry processing, pages 89–98. Citeseer.

Boyd, S. and Vandenberghe, L. (2018). Introduction to

applied linear algebra: vectors, matrices, and least

squares. Cambridge university press.

Brüel-Gabrielsson, R., Ganapathi-Subramanian, V., Skraba,

P., and Guibas, L. J. (2020). Topology-aware surface

reconstruction for point clouds. In Computer Graph-

ics Forum, volume 39, pages 197–207. Wiley Online

Library.

Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan,

P., Huang, Q., Li, Z., Savarese, S., Savva, M.,

Song, S., Su, H., et al. (2015). ShapeNet: An

information-rich 3D model repository. arXiv preprint

arXiv:1512.03012.

Douglas, D. H. and Peucker, T. K. (1973). Algorithms for

the reduction of the number of points required to rep-

resent a digitized line or its caricature. Cartographica:

the international journal for geographic information

and geovisualization, 10(2):112–122.

Fan, H., Su, H., and Guibas, L. J. (2017). A point set gener-

ation network for 3D object reconstruction from a sin-

gle image. In Proceedings of the IEEE conference on

Curvy: A Parametric Cross-Section Based Surface Reconstruction

149

computer vision and pattern recognition, pages 605–

613.

Fey, M. and Lenssen, J. E. (2019). Fast graph represen-

tation learning with PyTorch Geometric. In ICLR

Workshop on Representation Learning on Graphs and

Manifolds.

Floater, M. S. and Surazhsky, T. (2006). Parameterization

for curve interpolation. In Studies in Computational

Mathematics, volume 12, pages 39–54. Elsevier.

Gadelha, M., Wang, R., and Maji, S. (2018). Multireso-

lution tree networks for 3D point cloud processing.

In Proceedings of the European Conference on Com-

puter Vision (ECCV), pages 103–118.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2020). Generative adversarial networks. Com-

munications of the ACM, 63(11):139–144.

Hamilton, W. L., Ying, R., and Leskovec, J. (2017). In-

ductive representation learning on large graphs. In

Proceedings of the 31st International Conference on

Neural Information Processing Systems, pages 1025–

1035.

Han, Z., Wang, X., Liu, Y.-S., and Zwicker, M. (2019).

Multi-angle point cloud-VAE: Unsupervised feature

learning for 3D point clouds from multiple angles by

joint self-reconstruction and half-to-half prediction. In

2019 IEEE/CVF International Conference on Com-

puter Vision (ICCV), pages 10441–10450. IEEE.

Huang, J. and Menq, C. (2002). Combinatorial manifold

mesh reconstruction and optimization from unorga-

nized points with arbitrary topology. Computer-Aided

Design, 34(2):149–165.

Huang, Z., Carr, N., and Ju, T. (2019). Variational implicit

point set surfaces. ACM Transactions on Graphics

(TOG), 38(4):1–13.

Huang, Z., Zou, M., Carr, N., and Ju, T. (2017). Topology-

controlled reconstruction of multi-labelled domains

from cross-sections. ACM Transactions on Graphics

(TOG), 36(4):1–12.

Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Poisson

surface reconstruction. In Eurographics.

Kipf, T. N. and Welling, M. (2017). Semi-supervised classi-

ﬁcation with graph convolutional networks. In 5th In-

ternational Conference on Learning Representations,

ICLR 2017.

Kuhn, H. W. and Tucker, A. W. (2014). Nonlinear program-

ming. In Traces and emergence of nonlinear program-

ming, pages 247–258. Springer.

Lazar, R., Dym, N., Kushinsky, Y., Huang, Z., Ju, T., and

Lipman, Y. (2018). Robust optimization for topo-

logical surface reconstruction. ACM Transactions on

Graphics (TOG), 37(4):1–10.

Lin, C.-H., Kong, C., and Lucey, S. (2018). Learning ef-

ﬁcient point cloud generation for dense 3D object re-

construction. In proceedings of the AAAI Conference

on Artiﬁcial Intelligence, volume 32.

Liu, L., Bajaj, C., Deasy, J. O., Low, D. A., and Ju,

T. (2008). Surface reconstruction from non-parallel

curve networks. In Computer Graphics Forum, vol-

ume 27, pages 155–163. Wiley Online Library.

Memari, P. and Boissonnat, J.-D. (2008). Provably good 2D

shape reconstruction from unorganized cross-sections.

In Computer Graphics Forum, volume 27, pages

1403–1410. Wiley Online Library.

Park, J. J., Florence, P., Straub, J., Newcombe, R., and

Lovegrove, S. (2019). DeepSDF: Learning continuous

signed distance functions for shape representation. In

The IEEE Conference on Computer Vision and Pattern

Recognition (CVPR).

Peng, S., Jiang, C., Liao, Y., Niemeyer, M., Pollefeys, M.,

and Geiger, A. (2021). Shape as points: A differen-

tiable poisson solver. Advances in Neural Information

Processing Systems, 34:13032–13044.

Sarmad, M., Lee, H. J., and Kim, Y. M. (2019). RL-GAN-

Net: A reinforcement learning agent controlled gan

network for real-time point cloud shape completion.

In Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition, pages 5898–

5907.

Sawdayee, H., Vaxman, A., and Bermano, A. H.

(2022). Orex: Object reconstruction from planner

cross-sections using neural ﬁelds. arXiv preprint

arXiv:2211.12886.

Sharma, O. and Agarwal, N. (2017). Signed distance based

3D surface reconstruction from unorganized planar

cross-sections. Computers & Graphics, 62:67–76.

Van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-SNE. Journal of machine learning research,

9(11).

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Liò,

P., and Bengio, Y. (2018). Graph attention networks.

In 6th International Conference on Learning Repre-

sentations, ICLR 2018.

Wen, X., Li, T., Han, Z., and Liu, Y.-S. (2020). Point cloud

completion by skip-attention network with hierarchi-

cal folding. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 1939–1948.

Yin, K., Huang, H., Cohen-Or, D., and Zhang, H. (2018).

P2p-net: Bidirectional point displacement net for

shape transform. ACM Transactions on Graphics

(TOG), 37(4):1–13.

Zhou, K., Huang, X., Li, Y., Zha, D., Chen, R., and Hu, X.

(2020). Towards deeper graph neural networks with

differentiable group normalization. Advances in Neu-

ral Information Processing Systems, 33:4917–4928.

Zou, M., Holloway, M., Carr, N., and Ju, T. (2015).

Topology-constrained surface reconstruction from

cross-sections. ACM Transactions on Graphics

(TOG), 34(4):1–10.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

150