A Framework for Reproducible Parallel DNA String Matching

Ricardo Regis Cavalcante Chaves

and Alba Cristina Magalhaes Alves de Melo

Dep. of Computer Science, Campus Universitario Darcy Ribeiro, University of Brasilia, Brasilia, Brazil

Keywords:

Reproducibility, Approximate String Matching, Parallel Sequence Comparison.

Abstract:

In this paper, we propose an output reproducible framework that executes parallel sequence comparison algo-

rithms, computing the edit distance. The framework generates tables/graphics and linear regressions that can

be used to predict the execution times. We also propose parallel OpenMP versions of serial algorithms (DP

and UK) used to compute the edit distance. Our parallel DP is antidiagonal block-based, where the blocks that

belong to the same set of antidiagonals are assigned to different threads, which compute them simultaneously.

Due to data dependencies presented by UK, we opted to compute each antidiagonal in parallel. Our results

with synthetic and real sequences show that the parallel UK version presents the best execution times in most

cases. We also show that the linear regressions generated by our tool have errors below 10%, on average.

1 INTRODUCTION

Even though reproducibility is a key concept in sci-

ence, it is often neglected. According to (Gundersen,

2021), there are three different types of reproducibil-

ity: (a) outcome: the outcome of the reproducibility

experiment is the same as the output of the original

experiment; (b) analysis: the outputs are not the same

but the same analysis can be made; (c) interpretation:

neither the outputs nor the analyses are the same but

the same conclusion can be reached. Recently, a lot of

effort has been made in reproducibility, since it has a

direct impact on the results’ reliability. Besides being

able to reproduce results, other functionalities are im-

portant, such as expressiveness and prediction (Wrat-

ten et al., 2021). We claim that scientiﬁc experiments

should be at least outcome reproducible, with tools

that provide ease of use and expressiveness.

The growth of massive amounts of biological data

has created an increasing demand for tools to assist

researchers in analyzing these data. The use of these

computational tools can improve conﬁdence in pub-

lished results, allow double-checking them by other

researchers, and facilitate redoing the entire experi-

ment. Therefore, in order to ease replication efforts,

there is a need for more openly available tools.

There are many bioinformatics frameworks avail-

able, such as Bioconductor (Huber et al., 2015),

Galaxy (Price et al., 2024), and Biopython (Cock

https://orcid.org/0000-0002-5910-8716

https://orcid.org/0000-0001-5191-5209

et al., 2009). Although these frameworks have a set

of features like maturity, extensibility and high mod-

ularity, they are not focused on parallel algorithms. In

particular, Bioconductor is a widely used framework

for the analysis of high-throughput genomic data and

it is based on the R programming language. Galaxy

is a web-based platform for managing bioinformatics

workﬂows with great focus on training and education.

Biopython is a set of tools for biological computation

written in Python to interact with biological databases

and integrate with other bioinformatics tools.

In order to generate results easily and make the

execution of experiments reproducible, we designed

a reproducible framework that executes a given algo-

rithm multiple times, varying the parameters required

by the execution scenarios. At the end of the exe-

cution, the framework generates several graphics and

presents them to the user. Besides that, the tool has

a module that generates linear regressions, which can

be used for execution time prediction.

As a case study, we chose the Approximate String

Matching (ASM) problem. ASM computes the simi-

larity degree between two strings, where a high sim-

ilarity degree means very few differences (Hall and

Dowling, 1980). For ASM, the most widely used met-

ric is the edit distance or Levenshtein distance (Leven-

shtein, 1966), which determines the minimum num-

ber of operations needed to transform one string into

another. Since the 1970s, the ASM problem is for-

mulated as dynamic programming (DP) (Wagner and

Fischer, 1974; Sellers, 1974) and this is the most used

Chaves, R. R. C. and Alves de Melo, A. C. M.

A Framework for Reproducible Parallel DNA String Matching.

DOI: 10.5220/0013302600003911

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 18th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2025) - Volume 1, pages 661-668

ISBN: 978-989-758-731-3; ISSN: 2184-4305

661

approach (Berger et al., 2021). In this case, a DP ma-

trix is computed with size n × m, where n and m are

the lengths of the sequences.

In this paper, we deal with unrestricted ASM al-

gorithms, which do not restrict the problem to a max-

imum error k nor do not limit the size of one of the

strings. The algorithms considered are DP (Wagner

and Fischer, 1974) and UK (Ukkonen, 1983). In par-

ticular, UK is an algorithm with pruning, i.e., it does

not compute the entire DP matrix in most cases. In

practice, string matching has many applications be-

yond text search such as: computational biology, pat-

tern recognition, computer vision, among others. In

this paper, we will focus on computational biology.

Sequence alignment algorithms, such as Smith-

Waterman and Needleman-Wunsch, are also used in

many tools (Figueiredo et al., 2021; Schmidt et al.,

2024) and they compute differently the DP matrix.

Even though there are widely used, they are outside

the scope of this paper.

We propose a reproducibility framework and par-

allel implementations for the algorithms DP and UK,

using the OpenMP programming interface. Parallel

DP is a block-based approach which always computes

the entire DP matrix. Parallel UK has pruning ca-

pabilities computing, on the average case, much less

than DP.

Our results show that, depending on the dissim-

ilarity between the sequences and their lengths, one

algorithm performs better than the other. For the syn-

thetic sequences compared, Parallel UK performed

better in most cases. For the real SARS-CoV-2 DNA

sequences case study, Parallel UK also performed bet-

ter than DP in most comparisons. This happened be-

cause the sequences have low dissimilarity and are

considerably long.

The remainder of this paper is organized as fol-

lows. Section 2 presents the ASM problem and the

DP and UK algorithms used to solve it. Section 3

presents the design of our reproducible framework

and the parallel algorithms integrated to it. Section

4, experimental results are presented for synthetic se-

quences and real SARS-CoV-2 DNA sequences. Fi-

nally, Section 5 concludes the paper.

2 APPROXIMATE STRING

MATCHING (ASM)

2.1 Overview

String matching is a classical problem involving

strings that searches for occurrences of a pattern P in

a text T (Navarro, 2001). Exact string matching ﬁnds

the exact pattern P in text T whereas Approximate

String Matching is an approach of ﬁnding strings that

match P approximately, i.e., allowing errors.

For ASM, the alphabet is deﬁned as a ﬁnite set

of symbols (characters) and represented by Σ, where

|Σ| denotes the length of the alphabet. For compar-

ing DNA sequences, the alphabet is Σ = {A, T, G,C}

and |Σ| = 4. For computational biology ASM applica-

tions, the term sequence is used instead of string and

the character that occurs in position i of T (or P) is

denoted by T

(or P

The goal of ASM is to ﬁnd approximate occur-

rences (matchings) of P (called P

′

) in T when a cer-

tain tolerance is allowed and a degree of similarity is

enough to satisfy the match (P ≈ P

′

ASM algorithms use a distance function d(T, P),

for measuring the similarity of two strings (Navarro,

2001). One of the most widely used distance func-

tions is the edit distance or Levenshtein distance (Lev-

enshtein, 1966). The metric ed(T, P) computes the

minimal number of operations that are executed in P

in order to obtain P = P

′

. The operations are: (i) in-

sertion, when P

′

has an extra character, i.e. P

= ε,

where ε corresponds to the empty string; (ii) deletion,

when P has an extra character, i.e. P

′

= ε; (iii) substi-

tution, when P

and P

′

have different characters.

T T

0 0

0 0 0 0 0

1 1 1 1 1

2 1

1 2 2 1

2 1 1 1 2 2

2 2 2 2

3 3

(a)

-2 -1

1 2

-4

9∞ 9∞ 9∞ 9∞ 9∞

-3

9∞ 9∞ 9∞ 9∞

-2

9∞ 9∞ 9∞

-1

9∞ 9∞

0 3

9∞

-1 2

9∞ 9∞

-1

3 5

9∞ 9∞ 9∞

-1

9∞ 9∞ 9∞ 9∞

-1

9∞ 9∞ 9∞ 9∞ 9∞

-1

(b)

Figure 1: (a) DP matrix with edit distance highlighted at

bottom-right corner and (b) UK matrix with edit distance

highlighted at row n − m.

2.2 Algorithm DP (Wagner & Fischer

1974)

The DP algorithm (Wagner and Fischer, 1974) is

based on dynamic programming (DP). It compares

two strings T and P with m and n characters, respec-

tively, by computing a DP matrix C of size (m + 1,

n + 1). To create the DP matrix, the ﬁrst DP cell is set

to zero (C

0,0

= 0). Then, the cells which belong to the

BIOINFORMATICS 2025 - 16th International Conference on Bioinformatics Models, Methods and Algorithms

662

ﬁrst row are initialized with column index ( j) and the

cells belonging to the ﬁrst column are initialized with

(i). The remaining values are calculated with Equa-

tion 1. Time complexity of DP is O(mn). In the case

of a match (i.e., the characters T

and P

, are the same)

δ(x

, y

) = 0; and δ(x

, y

) = 1, otherwise.

i, j

= min











i−1, j−1

+ δ(x

, y

i−1, j

+ 1

i, j−1

+ 1

(1)

Figure 1(a) presents matrix C produced by Algo-

rithm DP when comparing strings T = CT TAGT and

P = CTACT . In this case, the edit distance is 2.

2.3 Algorithm UK (Ukkonen, 1983)

Ukkonen’s algorithm (Ukkonen, 1983) (UK) is based

on theoretical properties of the DP matrix computa-

tion when the metric used is edit distance. Ukkonen

noticed that the diagonals values of the DP matrix in-

crease monotonically from the upper-left to the lower-

right cells, i.e., the values of adjacent cells can differ

at most by one: 0 ≤ C

i, j

−C

i−1, j−1

≤ 1.

Hence, in his algorithm a new matrix L is build

based on this property since it is only necessary to

store the information about the position of the diag-

onal where the value is incremented. L(d, e) is cal-

culated, where d corresponds to the diagonal and e is

the edit distance computed so far, i. e., the maximum

row number of the DP matrix where the value e oc-

curs in a given diagonal d. In the initialization step,

L(d,|d|−1) = |d|−1 when d < 0, L(d, |d|− 1) = −1

when d ≥ 0 and L(d, e) = −∞ when e < d. The

remaining values of L are calculated after obtaining

the maximum of the three previously deﬁned values

(upper-left diagonal, left and bottom-left diagonal el-

ements) and then increasing the value while a match

occurs between T

and P

. Time complexity of UK is

O(ed(T, P).min(m, n)), where ed is the edit distance

between T and P.

Figure 1(b) presents the L matrix for comparing

strings T = CT TAGT and P = CTACT . In this case,

the edit distance is 2, i.e., the row where the maximum

value (5) occurs in matrix C.

3 REPRODUCIBILITY

FRAMEWORK

In Section 3.1 we propose our reproducibility frame-

work to execute the parallel algorithms. Sections 3.2

and 3.3 describe the parallel versions.

seqﬁle

Execution

Module

Raw Output

Data

Import

Module

Data

Preprocessing

Module

Data

Visualization

Module

Linear

Regression

Module

Data

Export

Module

Figure 2: Reproducibility Framework.

3.1 Reproducibility Framework

We designed a reproducibility framework that auto-

matically executes the experiments, collects the re-

sults and runs statistical analysis. The framework

was developed using IPython Notebook (P

erez and

Granger, 2007), a computational workbook environ-

ment for running Python. Furthermore, it provides

features such as the ability to run code in a cell-by-cell

basis and a collection of libraries. In particular, we

make use of the Numerical Python library (NumPy)

and the Matplotlib library.

In order to start the framework execution (Figure

2), a text ﬁle containing a list of FASTA ﬁles to be

compared (seqﬁle) and a set of parameters should be

provided as input for the execution module.

As input parameters, the Execution Module (Al-

gorithm 1) receives (a) the names of ﬁles containing

all pairs of sequences to be compared (seqﬁle); (b) the

algorithm (DP, UK or both); (c) the number of threads

(may be a range); (d) the number of repetitions for

each execution; and (e) the block size, needed for

running parallel DP. Every time the execution mod-

ule runs the algorithm, the output is appended to an

output ﬁle. The details of how the algorithms are ex-

ecuted are shown in Algorithm 1 and a sample seqﬁle

can be seen in Table 1.

Algorithm 1: Execution module pseudocode.

1: for 1 to THREAD QUANTITY do

2: for each SEQFILE do

3: Create temporary output directory

4: for each SEQUENCE PAIR do

5: for each ALGORITHM do

6: Create the output ﬁle

7: for 1 to REPEATS do

8: Execute algorithm

9: Append the output to ﬁle

10: end for

11: end for

12: end for

13: end for

14: end for

The Data Import Module reads the output ﬁles in

A Framework for Reproducible Parallel DNA String Matching

663

Table 1: A seqﬁle consists of a list of pairs of FASTA ﬁles

containning the sequences to be compared.

”./data/NC 045512.2.fasta” , ”./data/OP537480.1.fasta”

”./data/NC 045512.2.fasta” , ”./data/OP809597.1.fasta”

”./data/NC 045512.2.fasta” , ”./data/OP883605.1.fasta”

”./data/NC 045512.2.fasta” , ”./data/OQ026463.1.fasta”

”./data/NC 045512.2.fasta” , ”./data/OQ050253.1.fasta”

raw format from the Execution Module and parses

them to a structured format. This module is also re-

sponsible to detect errors in the output ﬁles such as

missing values or inconsistent data due possible ﬁle

corruption, i.e., it is important to ensure the correct-

ness of the data before proceeding to the next steps.

In the Data Preprocessing Module, the framework

performs operations such as: ﬁltering, to remove data

that is not relevant for the analysis; splitting, to sep-

arate the data in different categories; and grouping,

to organize and summarize sets of data. These opera-

tions are necessary to help the user to identify patterns

and trends in the data.

The Data Visualization Module generates compar-

ison tables and heatmaps from the processed data.

Heatmaps are useful to visualize the execution times

of the algorithms, where the color intensity is pro-

portional to the execution time. A table can be con-

structed using colors to identify and categorize data

with particular properties.

The linear regression models calculated with the

data collected in the experiments can help to predict

the execution times of future experiments. Besides

the regression equation, it also outputs other statistical

measures, such as the p-value, the standard error of

the estimate, and the R

coefﬁcient of determination.

The Data Export Module saves the processed data

in human friendly formats. In addition to CVS, it is

also possible to export in LaTex and Excel formats.

These formats can be easily imported into other tools

for further analysis.

3.2 Parallel DP Design

In the DP algorithm (Section 2.2), the dependencies

for cell (i, j) are (i − 1, j − 1), (i, j − 1) and (i − 1, j)

(Equation 1). So, all elements of antidiagonal d may

be computed in parallel, as soon as antidiagonal d − 1

is computed. However, depending on the size of the

matrix, the parallelism obtained when computing the

antidiagonalis in parallel may be small. In order to

increase the parallelism, we use a block-based ap-

proach, which considers blocks of antidiagonals. In

this case, each thread computes a block sequentially,

in parallel with the other threads (Figure 3a).

The DP matrix is divided into blocks of cells and

each block is assigned to a thread. When a thread

(a) Parallel DP (b) Parallel UK

Figure 3: (a) Parallel DP: blocks are computed by anti-

diagonal, but each block submatrix is computed sequen-

tially. (b) Parallel UK: the cells of each column are com-

puted in parallel.

ﬁnishes to compute a blocked antidiagonal, the last

row and the last column of each block are used as

initial values to the computation of the next antidiag-

onal. Since the blocks are computed in an antidiago-

nal fashion, the ﬁrst block to be computed is the one

in the upper-left corner of the matrix (antidiagonal 1)

and the last one is the one in the lower-right corner

(antidiagonal 5).

Algorithm 2: Parallel DP pseudocode.

1: do in parallel num threads

2: initialize DP matrix

3: split DP matrix in blocks

4: do in parallel num threads

5: for each tile do

6: execute dp in block

7: end for

8: return score

Algorithm 2 presents Parallel DP. In the initializa-

tion phase (lines 1-2), the OpenMP directive PARAL-

LEL FOR is used to parallelize the loops that initialize

the DP matrix. In the execution phase (lines 3-7), the

DP matrix is divided into square blocks of speciﬁed

size and then the inner loop (lines 5-6) is responsible

to compute each block among the threads using the

recurrence relation shown in Equation 1.

3.3 Parallel UK Design

In Parallel UK, we opted to compute each row in the

L matrix in parallel, since cells ranging from −e ≤

d ≤ +e can be calculated independently. This hap-

pens because, in UK, the computation of each cell de-

pends on the values of three cells from the previous

column: upper-left cell, left cell and bottom-left cell

(Figure 3b).

Algorithm 3 presents Parallel UK. Lines 1-2 ini-

tialize the UK matrix in parallel by ﬁlling the upper

and lower diagonals of the triangular shaped matrix.

Lines 3-11 show the execution loop, executed in par-

allel with num threads until the algorithm reaches a

BIOINFORMATICS 2025 - 16th International Conference on Bioinformatics Models, Methods and Algorithms

664

Algorithm 3: Parallel UK pseudocode.

1: do in parallel num threads

2: initialize UK matrix

3: do in parallel num threads

4: for each column e do

5: for each row d do

6: calculate column d, e

7: if score is found then break

8: end for

9: end for

10: return score

stop condition (line 7). Line 10 returns the calculated

score.

4 EXPERIMENTAL RESULTS

Parallel DP (Section 3.2) and Parallel UK (Sections

3.3) were implemented in C++ and OpenMP 5.3,

compiled with the GNU g++ compiler version 11.3.0

with no optmization ﬂag. The reproducibility frame-

work was implemented in Python. Our experiments

were collected in a desktop with an Intel Core i5-8400

Coffee Lake 2.8GHz (6 cores) with 32GB of RAM

running Ubuntu Linux 22.04. In the experiments, we

used synthetic and real DNA sequences.

Table 2: Execution times (ms) for synthetic sequences (se-

rial).

SERIAL EXEC TIME (ms)

SIZE 1000 5000 10000 30000

DISS DP UK DP UK DP UK DP UK

0 16.35 0.03 401.70 0.22 1606.58 0.46 14469.48 2.44

10 18.16 0.97 443.95 23.33 1763.24 93.47 15864.51 945.74

20 19.71 2.50 482.17 61.64 1917.30 263.00 17374.97 2633.44

30 21.05 4.48 519.32 119.76 2075.56 499.06 18674.96 5081.58

40 23.08 7.00 569.53 190.72 2244.12 793.45 20205.88 8291.49

50 25.10 10.02 595.86 285.13 2394.99 1154.82 21417.63 12258.71

60 26.64 13.59 608.32 391.16 2401.68 1608.85 21651.17 17578.00

70 25.20 17.94 589.80 513.59 2358.90 2116.55 21421.84 25229.88

80 23.38 21.99 581.76 639.51 2323.62 2642.07 20930.05 33539.03

90 24.46 26.31 573.97 750.47 2296.81 3130.46 20650.92 44322.13

100 23.35 31.92 567.29 874.63 2269.18 3697.26 20419.64 56972.07

Table 3: Execution times (ms) for synthetic sequences using

6 threads.

PARALLEL EXEC TIME (ms)

SIZE 1000 5000 10000 30000

DISS DP UK DP UK DP UK DP UK

0 4.22 0.19 79.65 0.41 307.39 0.65 2732.26 1.36

10 4.59 0.59 86.80 7.59 335.41 27.34 2990.96 238.81

20 4.97 1.07 93.82 16.58 363.25 63.09 3239.56 578.72

30 5.31 1.63 100.42 27.48 388.80 106.05 3474.35 1080.48

40 5.58 2.19 106.04 39.89 411.19 157.17 3690.27 1695.99

50 5.83 3.14 110.58 62.48 429.37 252.04 3838.69 2893.79

60 5.98 3.89 113.86 76.36 441.89 312.80 3962.96 3591.24

70 6.14 4.76 115.74 98.63 448.95 418.16 4032.16 5153.66

80 6.10 5.58 116.14 117.35 451.16 508.86 4057.45 6837.91

90 6.96 6.11 116.07 129.09 450.75 562.42 4065.38 8749.73

100 6.21 7.09 115.98 148.71 449.58 643.70 4060.20 11281.79

4.1 Results with Synthetic Sequences

The synthetic sequences were generated using ‘A’

characters as the reference text and sequences with

random replacements by the character ‘.’, depending

on the chosen dissimilarity. We generated sequences

of the following lengths: 1000, 2000, 5000, 10000,

and 30000 characters, increasing the dissimilarity be-

tween them varying from 0% (identical sequences)

to 100% (totally different sequences). Each experi-

ment was executed n times, depending in the value

provided in for the script’s input parameter (Section

3.1).

The results from the experiments conducted us-

ing synthetic sequences can be seen in Tables 2 and

3, with the heatmaps generated by our reproducibility

tool. The tables present (a) the dissimilarity between

the sequences, and (b) the total time (sum of initial-

ization time and execution time) for each comparison

as a result of running serial and parallel versions, re-

spectively.

In this case, by analyzing the execution times, we

were able to split them into two zones where the col-

ors indicate the performance of one algorithm in re-

lation to the other: (a) the green zone, where UK had

better performance than DP; and (b) the yellow zone,

where DP had better performance than UK. Consid-

ering the comparison between DP and UK, the se-

rial and parallel versions present similar behavior. It

can be seen that UK outperforms DP in most of the

comparisons, achieving the best execution time for se-

quences with dissimilarity ≤ 60%.

Figure 4 presents the graphic of execution time

generated by our framework.

The speedup achieved by parallel DP and parallel

UK is shown in Table 4. The speedup is calculated as

the ratio between the execution time of the serial im-

plementation and the parallel one, with 6 threads (one

thread running on each CPU core). It can be seen that

Parallel UK has low speedup with 0% dissimilarity.

This happens because the serial execution time is very

low (e.g. 0.03ms for sequences of size 1000). On the

other cases, very good speedups are obtained for both

Parallel DP and Parallel UK.

4.2 Linear Regression Analysis

The prediction of the execution time of parallel se-

quence comparison applications is very important,

specially when a great number of comparisons need to

be made. In this context, our reproducible tool gener-

ates linear regressions that can be used for execution

time prediction.

A Framework for Reproducible Parallel DNA String Matching

665

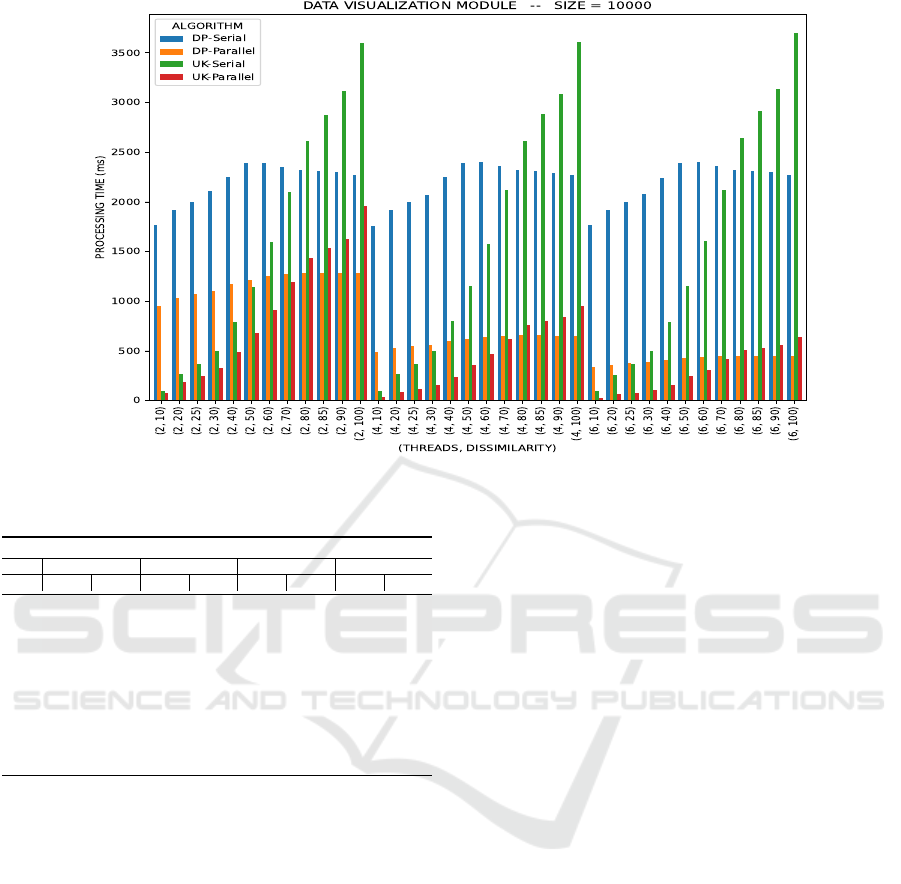
Figure 4: Execution times (ms) for comparing sequences of size 10000.

Table 4: Speedups for synthetic sequences.

SPEED-UP (SERIAL/PARALLEL)

SIZE 1000 5000 10000 30000

DISS DP UK DP UK DP UK DP UK

0 3.87× 0.16× 5.04× 0.54× 5.23× 0.71× 5.30× 1.79×

10 3.96× 1.64× 5.11× 3.07× 5.26× 3.42× 5.30× 3.96×

20 3.97× 2.34× 5.14× 3.72× 5.28× 4.17× 5.36× 4.55×

30 3.96× 2.75× 5.17× 4.36× 5.34× 4.71× 5.38× 4.70×

40 4.14× 3.20× 5.37× 4.78× 5.46× 5.05× 5.48× 4.89×

50 4.31× 3.19× 5.39× 4.56× 5.58× 4.58× 5.58× 4.24×

60 4.45× 3.49× 5.34× 5.12× 5.44× 5.14× 5.46× 4.89×

70 4.10× 3.77× 5.10× 5.21× 5.25× 5.06× 5.31× 4.90×

80 3.83× 3.94× 5.01× 5.45× 5.15× 5.19× 5.16× 4.90×

90 3.51× 4.31× 4.95× 5.81× 5.10× 5.57× 5.08× 5.07×

100 3.76× 4.50× 4.89× 5.88× 5.05× 5.74× 5.03× 5.05×

We opted to use multilinear regression models to

empirically estimate the execution time for differ-

ent input sizes, dissimilarity values and number of

threads, as shown in Equation 2.

ln(TIME) = a + b

× ln(SIZE)

+ b

× DISS

+ b

× THREADS

(2)

where TIME is the dependent variable that corre-

sponds to the execution time (ms), a is the y-intersect,

are the regression coefﬁcients, and the independent

variables are the SIZE (input size), DISS (dissimilar-

ity value in percentage), and THREADS (number of

threads used in the execution).

This linear regression model was used for the se-

rial and parallel versions of DP and UK. In each case,

the training used 77% of the data and the testing was

made with the remaining 23%. For training, we have

used pre-deﬁned lengths for input sizes (1000, 2000,

10000, 30000), dissimilarity values (10%, 20%, 30%,

40%, 50%, 60%, 70%, 80%, 90%, 100%), and num-

ber of threads (2, 4, 6). For prediction, we have used

the same values for number of threads (2, 4, 6), with

lengths 2500, 7500, 15000, 25000 for for input sizes

and values 25%, 45% and 85% for dissimilarity.

For the DP algorithm, the execution time was pre-

dicted using the following linear regression equations:

• Serial DP linear regression:

ln(y) = 2.97 + 1.99 × ln(SIZE) + 0.25 × DISS;

= 0.999

• Parallel DP linear regression:

ln(y) = 2.85 + 1.94 × ln(SIZE) + 0.32 × DISS

−0.24 × THREADS;

= 0.998

Table 5 presents the DP prediction results for 2,

4, 6 threads (TH), with sequence lengths 2500 and

15000 and dissimilarities 25%, 45% and 85%. In the

table, the lowest error is marked in bold and the high-

est error is underlined. It can be seen that our equa-

tions provide a quite accurate prediction, with all er-

rors below 15%. For the serial DP, most of the errors

are below 5% whereas most errors for parallel DP are

below 10%.

The execution time of the UK algorithm was pre-

dicted using the following linear regression equations:

• Serial UK linear regression:

ln(y) = 0.05 + 2.10 × ln(SIZE) + 3.81 × DISS;

= 0.987

• Parallel UK linear regression:

ln(y) = 0.45 + 2.02 × ln(SIZE) + 3.30 × DISS

−0.25 × THREADS;

= 0.987

BIOINFORMATICS 2025 - 16th International Conference on Bioinformatics Models, Methods and Algorithms

666

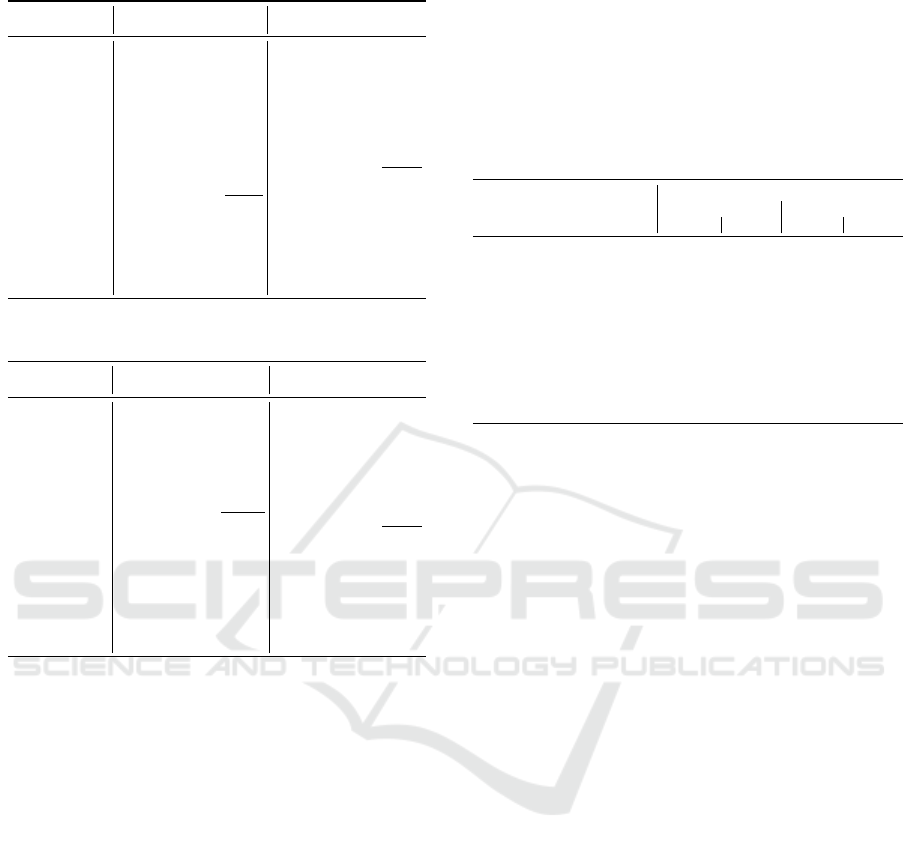
Table 5: Execution time prediction (ms) for DP.

TH. SIZE DISS

SERIAL PARALLEL

Real Predicted Error Real Predicted Error

2 2500 25% 125.08 126.92 1.47% 68.08 67.41 -0.98%

2 2500 45% 145.98 133.97 -8.23% 76.17 72.00 -5.47%

2 2500 85% 144.33 149.27 3.42% 81.26 82.13 1.07%

2 15000 25% 4485.88 4526.52 0.91% 2405.02 2241.57 -6.80%

2 15000 45% 5236.91 4778.10 -8.76% 2693.74 2394.09 -11.12%

2 15000 85% 5195.09 5323.97 2.48% 2912.31 2730.98 -6.23%

4 2500 25% 125.18 126.96 1.42% 36.25 40.88 12.77%

4 2500 45% 145.38 134.02 -7.81% 40.59 43.66 7.56%

4 2500 85% 144.28 149.33 3.50% 43.38 49.80 14.80%

4 15000 25% 4490.28 4528.18 0.84% 1222.05 1359.22 11.22%

4 15000 45% 5230.59 4779.85 -8.62% 1369.06 1451.71 6.04%

4 15000 85% 5256.54 5325.93 1.32% 1477.64 1655.99 12.07%

6 2500 25% 125.22 127.01 1.43% 26.25 24.79 -5.56%

6 2500 45% 145.48 134.07 -7.84% 29.29 26.47 -9.63%

6 2500 85% 144.43 149.38 3.43% 31.25 30.20 -3.36%

6 15000 25% 4540.56 4529.84 -0.24% 838.69 824.19 -1.73%

6 15000 45% 5231.09 4781.60 -8.59% 939.34 880.27 -6.29%

6 15000 85% 5230.48 5327.88 1.86% 1010.59 1004.14 -0.64%

Table 6: Execution time prediction (ms) for UK.

TH. SIZE DISS

SERIAL PARALLEL

Real Predicted Error Real Predicted Error

2 2500 25% 21.22 18.09 -14.75% 15.27 13.16 -13.82%

2 2500 45% 55.73 39.06 -29.91% 33.39 25.78 -22.79%

2 2500 85% 166.35 182.16 9.50% 86.49 98.97 14.43%

2 15000 25% 843.43 774.32 -8.19% 582.23 503.82 -13.47%

2 15000 45% 2203.47 1672.17 -24.11% 1339.80 987.14 -26.32%

2 15000 85% 6544.81 7798.35 19.15% 3522.62 3789.56 7.58%

4 2500 25% 20.87 18.09 -13.32% 8.17 7.95 -2.69%

4 2500 45% 53.78 39.06 -27.37% 17.45 15.57 -10.77%

4 2500 85% 168.21 182.15 8.29% 44.72 59.78 33.68%

4 15000 25% 845.73 774.28 -8.45% 276.61 304.32 10.02%

4 15000 45% 2239.91 1672.09 -25.35% 660.38 596.26 -9.71%

4 15000 85% 6513.57 7797.98 19.72% 1847.55 2288.98 23.89%

6 2500 25% 20.71 18.09 -12.65% 5.97 4.80 -19.60%

6 2500 45% 53.65 39.06 -27.19% 12.56 9.41 -25.08%

6 2500 85% 165.15 182.14 10.29% 31.94 36.11 13.06%

6 15000 25% 848.75 774.24 -8.78% 183.68 183.81 0.07%

6 15000 45% 2191.20 1672.01 -23.69% 431.14 360.15 -16.47%

6 15000 85% 6677.75 7797.61 16.77% 1264.54 1382.59 9.34%

Table 6 presents the prediction results for UK us-

ing 2, 4, 6 threads, with sequence lengths 2500 and

15000 and dissimilarities 25%, 45% and 85%. It

can be seen that, on average, the prediction errors

are higher for UK than DP, both in the serial and in

the parallel versions. This happens because UK has

pruning capability and the number of cells computed

depends on the dissimilarity between the sequences,

leading to a more complex behavior. For this rea-

son, we consider that a maximum error of 33.68% is

a good result, considering that most errors for UK are

below 20%.

4.3 Real DNA Sequences: Covid-19

Case Study

We also conducted a set of experiments using

real DNA sequences publicly available at the Na-

tional Center for Biotechnology Information (NCBI),

https://www.ncbi.nlm.nih.gov/. For the ﬁrst set of

experiments, we chose sequences from variants of

SARS-CoV-2 (lengths ∼ 29900) all over the world

were compared to the reference sequence SARS-

CoV-2 isolate Wuhan-Hu-1 (length = 29903) using

parallel DP and Parallel UK. The dissimilarity is ob-

tained by dividing the edit distance by the length of

the sequence. Values in bold highlight the best execu-

tion time for each comparison (Table 7).

Table 7: Execution times (ms) for the SARS-CoV-2 case

study. The dissimilarity is the result of dividing edit dis-

tance value by the length of the sequence.

COUNTRY DISS

EDIT

DIST.

TIME(ms)

DP UK

SERIAL PARAL. SERIAL PARAL.

Japan 7.11% 2082 20490.47 3992.93 224.02 40.03

Chile 0.64% 192 20768.15 4042.56 3.99 1.90

Australia 0.52% 156 20916.51 4036.69 3.34 1.76

France 0.7% 208 20749.34 4031.12 4.23 2.01

UK 0.44% 130 20786.62 4038.58 3.11 1.67

Canada 17.44% 5184 20659.38 4056.76 1311.57 231.02

Russia 0.83% 246 20724.72 4032.93 4.81 2.20

South Africa 0.54% 161 20732.42 4057.27 3.48 1.79

Libya 0.81% 242 20747.39 4043.30 4.68 2.18

India 1.02% 305 20779.65 4073.30 6.11 2.51

USA 0.76% 226 20808.56 4039.60 4.72 2.08

The results in Table 7 show Serial DP as the

algorithm with the worst performance among all

SARS-CoV-2 comparisons while Serial UK is no-

ticeably better. The high values of some edit dis-

tances – the case of Canada (OQ305820.1) and Japan

(LC753266.1) – is due to the presence of some long

chains of ‘N’ characters in their DNA sequences indi-

cating the impossibility of a correct identiﬁcation of

some parts of it. In all cases, Parallel UK performed

much better than Parallel DP.

It is possible to make a linking between the real

DNA sequences with the 30K-character-length syn-

thetic sequences from Tables 2 and 3. For the covid-

19 case study, the sequence sizes are about 30000. We

can see that all dissimilarities are below 20% and that

Serial and Parallel UK behaved much better than Se-

rial and Parallel DP. This is consistent with the result

obtained with the comparison of synthetic sequences

with length equal to 30000. Therefore, for SARS-

CoV-2 sequence comparisons, Parallel UK is the best

choice, particularly because hundreds or even thou-

sands of those sequences of SARS-Cov-2 are com-

pared in a unique biological study (Uraki, 2023; Teylo

et al., 2021; Hidalgo et al., 2022).

5 CONCLUSION

In this paper, we proposed a reproducible framework

to execute parallel sequence comparison algorithms.

Besides producing reproducible outputs, our frame-

work also generates linear regressions with the output

data, which are able to estimate the execution time of

future executions.

A Framework for Reproducible Parallel DNA String Matching

667

The use of the framework allowed us to automate

several repeatable tasks that are time consuming and

prone to errors, such as executing the algorithms with

correct parameters (Execution Module), collecting re-

sults from each execution (Data Import Module), pro-

cessing these results (Data Preprocessing Module),

generation of graphics (Data Visualization Module),

statistical analysis and linear regressions (Linear Re-

gression Module), and the data exporting to other for-

mats (Data Export Module). Furthermore, the modu-

lar design of the framework also allowed an easy in-

tegration of new algorithms.

Hence, OpenMP versions of two dynamic pro-

gramming algorithms (DP and UK) to compute the

edit distance between strings were also proposed and

evaluated. These algorithms were implemented in

C++ and executed in a multicore machine using the

proposed framework.

Our results with synthetic and real DNA se-

quences whose sizes ranged from 1000 to 30000 show

that our parallel versions are able to obtain very good

speedups (up to 5.88x, with 6 threads). Also, we show

that Parallel UK is the best choice for the majority of

the tests, producing the smallest execution time for

the synthetic and real sequences. Moreover, we show

that our framework generates automatically graphics,

simplifying the task of running experiments, and that

the linear regressions obtained with the framework

have very good statistical relevance (R

≥ 9.87), gen-

erating accurate execution time predictions.

As future work, we want to expand the linear re-

gression module of our framework, including addi-

tional plugins with machine learning strategies. In

addition, we want to incorporate other parallel ver-

sions of biological sequence comparison algorithms

for local and global alignment, such as MASA-

OpenCL (de Figueiredo Jr. et al., 2019), to our frame-

work. Finally, we intend to create a new module, that

will connect to the Data Export Module and use the

alignments produced by the executions in more com-

plex problems, such as Multiple Sequence Alignment.

REFERENCES

Berger, B., Waterman, M. S., and Yu, Y. W. (2021). Leven-

shtein distance, sequence comparison and biological

database search. IEEE Transactions on Information

Theory, 67(6):3287–3294.

Cock, P. J. A., Antao, T., Chang, J. T., Chapman, B. A., Cox,

C. J., Dalke, A., Friedberg, I., Hamelryck, T., Kauff,

F., Wilczynski, B., and de Hoon, M. J. L. (2009).

Biopython: freely available Python tools for compu-

tational molecular biology and bioinformatics. Bioin-

formatics, 25(11):1422–1423.

de Figueiredo Jr., M. A. C., de Oliveira Sandes, E. F., Ro-

drigues, G. N., Teodoro, G. L. M., and de Melo, A.

C. M. A. (2019). Masa-opencl: Parallel pruned com-

parison of long dna sequences with opencl. Con-

currency and Computation: Practice and Experience,

31(11):e5039. e5039 cpe.5039.

Figueiredo, M., Navarro, J. P., Sandes, E. F. O., Teodoro,

G., and Melo, A. C. M. A. (2021). Parallel ﬁne-

grained comparison of long dna sequences in homo-

geneous and heterogeneous gpu platforms with prun-

ing. IEEE Transactions on Parallel and Distributed

Systems, 32(12):3053–3065.

Gundersen, O. (2021). The fundamental principles of repro-

ducibility. Philosophical Trans. of the Royal Society,

379:1–15.

Hall, P. A. V. and Dowling, G. R. (1980). Approx-

imate string matching. ACM Computing Surveys,

12(4):381–402.

Hidalgo, R., DeVito, A., Salah, N., S., V. A., and Mered-

ith, R. W. (2022). Inferring phylogenetic relationships

using the smith-waterman algorithm and hierarchical

clustering. In IEEE International Conference on Big

Data, pages 5910–5914. IEEE.

Huber, W., Carey, V. J., Gentleman, R., et al. (2015).

Orchestrating high-throughput genomic analysis with

bioconductor. Nature Methods, 12(2):115–121.

Levenshtein, V. I. (1966). Binary codes capable of correct-

ing deletions, insertions, and reversals. Soviet Physics

Doklady, 10:707–710.

Navarro, G. (2001). A guided tour to approximate string

matching. ACM Computing Surveys, 33(1):31–88.

Price, G., Nekrutenko, A., Gr

uning, B. A., and Schatz,

M. C. (2024). The Galaxy platform for accessible,

reproducible, and collaborative data analyses: 2024

update. Nucleic Acids Research, 52(W1):W83–W94.

erez, F. and Granger, B. E. (2007). Ipython: A system for

interactive scientiﬁc computing. Computing in Sci-

ence & Engineering, 9(3):21–29.

Schmidt, B., Kallenborn, F., Chacon, A., and Hundt,

C. (2024). CUDASW++4.0: ultra-fast GPU-based

Smith-Waterman protein sequence database search.

BMC Bioinformatics, 25(1):342.

Sellers, P. (1974). On the theory and computation of evo-

lutionary distances. SIAM Journal of Applied Mathe-

matics, 26:787–793.

Teylo, L., Nunes, A. L., Melo, A. C. M. A., Boeres, C.,

Drummond, L. M. A., and Martins, N. F. (2021).

Comparing sars-cov-2 sequences using a commercial

cloud with a spot instance based dynamic scheduler.

In IEEE/ACM International Symposium on Cluster,

Cloud and Internet Computing, pages 24–256. IEEE.

Ukkonen, E. (1983). On approximate string matching. In

International Conference on Fundamentals of Com-

putation Theory, pages 487–495. Springer.

Uraki, R. e. a. (2023). Characterization of sars-cov-2 omi-

cron ba.2.75 clinical isolates. Nature Communica-

tions, 14(1):1620.

Wagner, R. A. and Fischer, M. (1974). The string-to-string

correction problem. Journal of the ACM, 1:168–173.

Wratten, L., Wilm, A., and Goke, J. (2021). Reproducible,

scalable, and shareable analysis pipelines with bioin-

formatics workﬂow managers. Nature Methods,

18:1161–1168.

BIOINFORMATICS 2025 - 16th International Conference on Bioinformatics Models, Methods and Algorithms

668