Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model

Reuse for Changed State-Action Space

Feline Malin Barg

1 a

, Eric Veith

2 b

and Lasse Hammer

1 c

OFFIS e.V., Escherweg 2, 26121 Oldenburg, Germany

Carl von Ossietzky Universit

at, Ammerl

ander Heerstraße 114-118, 26129, Oldenburg, Germany

{feline.malin.barg, eric.veith, lasse.hammer}@ofﬁs.de

Keywords:

Reinforecment Learning, Soft-Actor-Critic, Transfer Learning, State-Action Space Change, Model Reuse.

Abstract:

Deep Reinforcement Learning (DRL) is a leading method for control in high-dimensional environments, ex-

celling in complex tasks. However, adapting DRL agents to sudden changes, such as reduced sensors or

actuators, poses challenges to learning stability and efﬁciency. While Transfer Learning (TL) can reduce

retraining time, its application in environments with sudden state-action space modiﬁcations remains underex-

plored. Resilient, time-efﬁcient strategies for adapting DRL agents to structural changes in state-action space

dimension are still needed. This paper introduces Actor-Critic Model Reuse (ACMR), a novel TL-based algo-

rithm for tasks with altered state-action spaces. ACMR enables agents to leverage pre-trained models to speed

up learning in modiﬁed environments, using hidden layer reuse, layer freezing, and network layer expansion.

The results show that ACMR signiﬁcantly reduces adaptation times while maintaining strong performance

with changed state-action space dimensions. The study also provides insights into adaptation performance

across different ACMR conﬁgurations.

1 INTRODUCTION

Deep Reinforcement Learning (DRL) has emerged as

a powerful tool for solving complex control problems

in dynamic environments (Henderson et al., 2018).

DRL combines Reinforcement Learning (RL) princi-

ples with the power of deep neural networks, enabling

agents to make decisions and learn adaptive strate-

gies in high-dimensional state-action spaces. This ca-

pacity has led to remarkable achievements in areas

like robotics with continuous control tasks (Arulku-

maran et al., 2017), and complex systems including

real-world infrastructure such as the power grid (Omi-

taomu and Niu, 2021). A key challenge with these

systems is the need not only for stable control un-

der normal conditions but also for adaptability when

components are added or removed. In the case of the

power grid, for example, when new components like

like a PV system are introduced or existing ones are

decommissioned, the agent’s state and action spaces

change, and it may lose or gain access to certain sen-

sors and actuators (Wolgast and Nieße, 2024). This

https://orcid.org/0000-0001-8753-7430

https://orcid.org/0000-0003-2487-7475

https://orcid.org/0009-0000-5202-5574

can severely impair the agent’s ability to perceive and

control its environment as it normally would. Simi-

larly, in robotics, the failure or addition of limbs can

dramatically alter the control task, requiring agents to

adjust their strategies to the new state-action space.

Adapting to these new conditions typically requires

extensive retraining, which can be time-consuming.

However, in the context of critical infrastructure or

or autonomous systems, there is often no time for

lengthy retraining processes (Nguyen et al., 2020).

Transfer Learning (TL) offers a potential solu-

tion by allowing DRL agents to reuse knowledge

from previously encountered environments to acceler-

ate learning in modiﬁed conditions (Taylor and Stone,

2009). While the power grid provides a compelling

application domain, current benchmarks for power

grid control often lack standardized testing frame-

works required to systematically evaluate advanced

DRL methods like TL. In contrast, robotic control

benchmarks such as Gymnasium’s Humanoid envi-

ronment (Towers et al., 2024) offer well-established,

high-dimensional testbeds with the ability to create

custom environments. This paper focuses on ap-

plying TL in a challenging DRL control environ-

ment: Gymnasium’s Humanoid environment. The

Humanoid environment requires an agent to control a

682

Barg, F. M., Veith, E. and Hammer, L.

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space.

DOI: 10.5220/0013304900003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 2, pages 682-692

ISBN: 978-989-758-737-5; ISSN: 2184-433X

complex multi-jointed ﬁgure, learning balance, loco-

motion, and continuous forward movement in a high-

dimensional state-action space. This task is particu-

larly sensitive to changes in the agent’s available con-

trols, making it an ideal testbed for investigating TL’s

efﬁcacy in environments with reduced sensory or ac-

tuator capacities. By leveraging the robust evaluation

framework provided by Gymnasium, we can derive

insights that are broadly applicable to other domains,

including critical infrastructure like the power grid.

To address the challenge of adapting a trained

agent to new environmental changes without lengthy

retraining, this paper introduces the Actor-Critic

Model Reuse (ACMR) algorithm. ACMR leverages

TL by reusing pre-trained models, and is demon-

strated here using the Soft Actor-Critic (SAC) algo-

rithm as an example. SAC, which is well-suited for

continuous control tasks (Haarnoja et al., 2018), com-

bines an actor-critic architecture with entropy maxi-

mization to provide both stability and robust explo-

ration—qualities that are crucial in environments with

modiﬁed state-action spaces.

In this study, several conﬁgurations of ACMR are

examined, each designed to adapt the agent’s policy

and value function efﬁciently to a target environment

with fewer available control inputs. The conﬁgura-

tions include hidden layer reuse, layer freezing, and

the addition of new network layers to match the mod-

iﬁed input-output dimensions of the Humanoid envi-

ronment. The aim is to assess how these transfer con-

ﬁgurations impact the agent’s adaptability and learn-

ing speed in the modiﬁed environment.

This paper is organized as follows: The Related

Work section reviews DRL and TL, highlighting chal-

lenges like distribution shifts. The Methods section

introduces ACMR for adapting to changes in state-

action spaces. The Testing ACMR chapter describes

the experimental setup, followed by the Results sec-

tion, which presents the ﬁndings. The Discussion

compares the ACMR conﬁgurations, and the Conclu-

sion outlines our contributions and future directions.

The main contribution of this paper is to introduce

and demonstrate the effectiveness of ACMR in accel-

erating adaptation to modiﬁed environments with re-

duced sensors and actuators.

2 RELATED WORK

2.1 Deep Reinforcement Learning

DRL combines RL with Deep Neural Networks

(DNN) to enable agents to make high-level decisions

in complex, high-dimensional spaces. At its core, RL

studies how an agent interacts with its environment

through trial and error to learn a policy π that maxi-

mizes cumulative rewards. (Arulkumaran et al., 2017)

In DRL, we deﬁne a state space S ∈ R

such that

∈ S represents the state of the environment at time

t, and an action space A ∈ R

such that a

∈ A repre-

sents actions taken by the agent. The agent’s policy is

expressed as a distribution over actions given a state,

denoted as a

∼ π

∗

(·|s

) The goal is to maximize the

cumulative reward, where the reward function R de-

ﬁnes the reward r

as follows:

= R(s

, a

, s

t+1

). (1)

The structure and dimensionality of the state-

action space S × A play a fundamental role in

deﬁning the agent’s capacity to perceive and act

within its environment. Signiﬁcant modiﬁcations to

this space—such as the loss of sensors or actua-

tors—affect the learned policy. This can be repre-

sented as a dimensional shift, where the state-action

space in a new environment S‘ × A‘ may have differ-

ent dimensions. Mathematically, if d(S × A) repre-

sents the dimensions of the state-action space, then

d(S × A) ̸= d(S‘ × A‘). (2)

Since the originally learned policy π

∗

is condi-

tioned on states and actions from the original space

S × A, it cannot directly adapt to the modiﬁed state-

action space S‘ × A‘, as the dimensionality mismatch

leaves the policy undeﬁned in regions outside the ini-

tial space. Formally, this incompatibility can be ex-

pressed as:

∗

(a|s) undeﬁned for (s, a) ∈ S × A‘. (3)

Therefore, the DRL agent must adapt or retrain, as

the initial policy cannot operate effectively in the new

state-action space. A central challenge in DRL lies in

enabling efﬁcient adaptation to such changes without

requiring full retraining, which is resource-intensive

and time-consuming (Amodei et al., 2018).

Some prior work has explored approaches to re-

duce training times, such as pre-trained models (Ce-

liberto Jr et al., 2010), but these studies typically

assume consistent state-action spaces between train-

ing and deployment environments. Consequently, a

gap remains in the applicability of DRL to dynami-

cally changing domains, such as in critical infrastruc-

tures and robotics, where state-action space dimen-

sions may vary signiﬁcantly (Nguyen et al., 2020).

In conclusion, a research gap exists in the limited

methods for DRL adaptation to modiﬁed state-action

spaces without substantial retraining.

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space

683

2.2 Transfer Learning in Deep

Reinforcement Learning

TL is a strategy that leverages knowledge from a

source domain to improve learning in a related tar-

get domain, which is especially valuable when the tar-

get domain lacks sufﬁcient training data (Weiss et al.,

2016). In TL, each domain has a distinct feature space

and marginal probability distribution: the source do-

main is represented by X

and P (X

), while the tar-

get domain is represented by X

and P (X

). Effec-

tive transfer is achievable when there are differences

between these feature spaces or distributions, specif-

ically when X

̸= X

or P (X

) ̸= P (X

) (Pan and

Yang, 2010).

In the context of DRL, TL techniques often in-

volve reusing components such as policies, value

functions, or pre-trained hidden layers from source

domains to target domains (Fern

andez and Veloso,

2006b). A common assumption is that the dimen-

sionality of the state-action spaces remains consistent

between the source and target environments, which

allows for a direct transfer of learned knowledge

without requiring structural modiﬁcations (Zhu et al.,

2023).

However, in more dynamic environments, such

as critical infrastructure management or robotics, the

state-action space of an agent can undergo signiﬁ-

cant dimensional changes, posing challenges to tra-

ditional TL approaches. In such cases, knowledge

must be transferred from a source domain with one

state-action space dimension to a target domain with

a different state-action space dimension. Formally, let

the source domain have a state space S

⊆ R

and ac-

tion space A

⊆ R

, while the target domain has a

state space S

⊆ R

and action space A

⊆ R

. TL

requires adapting the actor and critic models of a pol-

icy π

: S

→ A

from the source domain to a policy

: S

→ A

in the target domain, where:

̸= n

or m

̸= m

. (4)

This adaptation involves a mapping or transfor-

mation T applied to both the actor and critic models

to handle the dimensional or structural mismatch be-

tween the source and target domains:

) = T

actor

(π

)), Q

, a

) = T

critic

, a

)),

(5)

where s

∈ S

, s

∈ S

, a

∈ A

, and a

∈ A

. Since

direct transfer is not feasible in this case, new ap-

proaches are needed to enable TL across differing

state-action space dimensions.

Although TL in DRL has been extensively stud-

ied across domains such as gaming (Tan et al., 2022),

robotics (Nair et al., 2018), and trafﬁc engineering

(Xu et al., 2020), limited research addresses the chal-

lenge of adapting to these dimensional shifts in state-

action spaces. For instance, (Beck et al., 2022) ex-

plore reduced action spaces within the same dimen-

sionality, while (Parisotto et al., 2015) examine model

transfer across different video games. There is sub-

stantial work on policy transfer, particularly through

policy distillation methods (Zhu et al., 2023), but

research on policy reuse is comparatively limited.

An example of policy reuse is the probabilistic pol-

icy reuse framework introduced in (Fern

andez and

Veloso, 2006b), yet no existing approaches tackle

the problem of adapting to signiﬁcant shifts in state-

action space dimensions as described above. This gap

highlights a need for TL reuse methodologies tailored

to enable DRL adaptation in environments with sub-

stantially altered state-action space dimensions.

2.3 Marginal Distribution Shifts and

Structural Shifts

In dynamic environments, RL agents encounter two

primary types of distributional changes:

Marginal Distribution Shifts. These shifts refer to

changes in the probability distribution over a ﬁxed

state-action space. The dimensional structure of S×A

remains constant, but the distribution changes, which

we can represent as:

P(S × A) ̸= P‘(S × A) (6)

where S × A is unchanged, and only the probabil-

ity distribution shifts from P(S ×A) to P‘(S×A). This

type of shift can typically be addressed with policy

adjustments, as the agent’s observation and action ca-

pabilities remain the same. Approaches like domain-

adversarial training (Ganin et al., 2016) and conser-

vative Q-learning (Kumar et al., 2020) have been

proposed to enhance the stability and adaptability of

agents under these types of distributional changes

Structural Shifts. Structural shifts involve changes

to the dimensionality or components of the state-

action space, such as the addition or removal of sen-

sors or actuators. However, these shifts do not nec-

essarily alter the marginal distribution within any un-

changed subspaces. We represent this as:

S × A ̸= S‘ × A‘ (7)

where S × A represents the original space and

S‘ × A‘ represents the modiﬁed space. While ap-

proaches like (Fern

andez and Veloso, 2006a) enable

policy transfer across tasks with structural shifts like

the state-action space change, the process of learn-

ing the mapping between differing dimensionalities is

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

684

time-intensive. This highlights the need for methods

that enable faster adaptation to such changes.

2.4 Research Gap and Challenges

Structural shifts pose a signiﬁcant challenge in RL, as

they involve changes to the dimensional structure of

the state-action space, and mapping methods for such

shifts are often time-intensive. TL offers a promising

solution, as it allows for knowledge transfer between

domains, potentially reducing the need for extensive

retraining. However, existing RL and TL methods

generally assume a stable state-action space structure

(Zhu et al., 2023), limiting their applicability in en-

vironments with frequent structural changes, such as

power grids or robotics. This research gap under-

scores the need for methods that enable RL agents

to adapt effectively across different state-action space

dimensions without exhaustive retraining—a crucial

capability for real-world, dynamically evolving envi-

ronments.

3 METHODS

3.1 The Changed State-Action Space

Problem

In achieving resilience for DRL agents, a primary

challenge is enabling adaptability to unexpected en-

vironmental changes without extensive retraining.

While fully eliminating retraining isn’t feasible, re-

ducing the training time needed for adaptation is a re-

alistic goal. In this work, we address the state-action

space problem directly: the source domain, represent-

ing the original, unchanged environment, provides

transferable knowledge, while the target domain has

a reduced state-action space due to fewer sensors and

actuators.

To select a suitable TL approach, we apply the di-

mensions of comparison (Taylor and Stone, 2009).

Here, the agent’s objective remains consistent be-

tween domains, eliminating the need for additional

domain mapping. Based on its robustness to unex-

pected events and entropy-driven exploration, we use

the SAC algorithm. The transferable knowledge con-

sists of the actor and critic models from the SAC agent

in the source domain, facilitating efﬁcient adaptation

to the target domain.

In summary, leveraging the source domain’s actor

and critic models in the target domain offers an efﬁ-

cient solution for managing state-action space reduc-

tions. This approach is formalized in the Actor-Critic

Table 1: Overview of ACMR conﬁgurations.

Freeze Hidden Layer Tra. Layer Expansion

No Conf. 1 Conf. 3

Yes Conf. 2 Conf. 4

Model Reuse (ACMR) algorithm, which we detail in

the following section.

3.2 Actor-Critic Model Reuse

ACMR is a novel TL algorithm that accelerates DRL

agent adaptation to environments with altered state-

action spaces, enabling rapid adaptation using knowl-

edge from a source environment without full retrain-

ing.

3.2.1 Explanation of ACMR

ACMR is based on the actor-critic architecture com-

mon in DRL, where an agent is composed of two main

components:

• The Actor: Responsible for selecting actions

based on the current state using a policy function,

π(a|s).

• The Critic: Evaluates the chosen actions by es-

timating the expected cumulative reward, or Q-

value, using a Q-function, Q(a|s).

In ACMR, these components are transferred from

a pre-trained agent (teacher agent A

= (π

, Q

)) to

a new agent (student agent A

= (π

, Q

)) facing an

altered environment. Rather than discarding learned

models, ACMR selectively reuses the actor and critic

components to speed up learning. However, given the

change in state-action space, a direct transfer of model

weights is typically not feasible. ACMR tackles this

by using ﬂexible transfer conﬁgurations that adapt

to dimensional discrepancies between the source and

target environments.

3.2.2 Transfer Conﬁgurations in ACMR

Four different conﬁgurations were implemented in

ACMR to enable model reuse across different state-

action dimensions. These conﬁgurations were com-

pared to identify the optimal one for ACMR and

shown in Table 1:

• Hidden Layer Transfer (Conf. 1): Only hidden

layers are transferred to the target agent, preserv-

ing learned features while adapting input and out-

put layers to the new state-action dimensions.

• Hidden Layer Transfer with Freezing (Conf. 2):

Hidden layers are transferred and frozen, main-

taining pre-trained values while training only the

input/output layers.

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space

685

• Layer Expansion (Conf. 3): Additional layers are

added to the input and output layers, allowing di-

rect transfer of all actor and critic layers by com-

pensating for dimensional differences.

• Layer Expansion with Freezing (Conf. 4): Sim-

ilar to layer expansion, but the transferred layers

are frozen, focusing learning on the newly added

layers.

The ﬁgure 1 shows the ACMR algorithm schemat-

ically, including the conﬁgurations:

SAC

teacher

SAC

student

Model Libary

Critic NN

Train

Actor NN

Sensors, Actuators, Reward

changed

Environments

Sensors, Actuators, Reward

Environments

Critic NN

Train

add model

use model

Add layer

Freeze layers

Actor NN

Figure 1: Schematic overview of the ACMR algorithm for

Changed State and Action Space.

Algorithm 1 outlines the ACMR algorithm, show-

ing how model parameters are reused based on differ-

ent conﬁgurations.

The implementation of ACMR was developed

based on the SAC algorithm provided by CleanRL

(vwxyzjn, 2024) for Gymansium environments on

GitHub. The code can be found on the GitHub reposi-

tory (Barg, 2024). No major adjustments were needed

to transfer the hidden layers, as they have a consistent

dimension. The hidden layers of the target agent (A

)

are simply overwritten with those of the source agent

) after initialization. To facilitate this process,

functions were added to save all necessary model pa-

rameters and dimension information after training A

A corresponding load function retrieves the selected

model from memory before starting the simulation,

speciﬁcally isolating the layers to be transferred and

using them for overwriting the target model’s layers.

The process is slightly different for conﬁgurations

that involve layer expansion. To adjust layer dimen-

sions, the actor and critic networks were modiﬁed by

Data: Source environment E

source

, Target

environment E

target

, Transfer option

trans f er type, Freeze option f reeze

Result: Adapted and trained actor-critic

model A

in E

target

Train A

in E

source

;

Save model parameters of A

(hidden layers,

output layers, observation/action space

information);

Initialize A

in E

target

;

if trans f er type == ”layer expansion” then

Load entire model parameters from A

into A

;

Add additional layers to actor and critic

networks in A

to match the state-action

space dimensions of E

target

;

end

if trans f er type == ”hidden layer transfer

only” then

Load only the hidden layers from A

into

;

end

foreach layer in A

if layer was loaded from A

then

if f reeze is True then

Disable gradient updates for this

layer to freeze it;

end

else

Initialize additional layers with

random weights if trans f er type is

”layer expansion”;

end

Train A

in E

target

;

Algorithm 1: Actor-Critic Model Reuse.

adding additional layers with ﬂexible dimensions be-

fore the input layer and/or after the output layer, de-

pending on the transferred layers. For the critic net-

work, only one layer was added before the input layer,

as the output layer consistently has a dimension of

1. For freezing, the selected layers were excluded

from future updates directly within the network con-

ﬁguration, ensuring that they retained their pretrained

weights throughout training in the target environment.

4 TESTING ACMR

To evaluate the effectiveness of the ACMR algorithm,

we utilize a well-established benchmark environment

for RL: Humanoid environment from Gymnasium

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

686

(Towers et al., 2024). This environment provides a

high-dimensional, continuous action and state space,

making it ideal for testing the adaptability of DRL

agents to state-action space changes.

4.1 The Environment

The Humanoid is a 2D bipedal robot with an ab-

domen, head, legs, and arms, designed to resemble

a human. The state-action space in this environment

can be modiﬁed by removing speciﬁc states and ac-

tions, allowing us to replicate scenarios where the

agent’s perception or control capabilities are reduced.

This change aligns with the core ACMR challenge:

Enabling a DRL agent to adapt efﬁciently to a lower-

dimensional state-action space by reusing the pre-

trained actor and critic models.

Two variations of the environment are used to

test ACMR: a source environment (the original

Humanoid) and a target environment (ArmlessHu-

manoid) with reduced state-action space.

• Humnaoid: The observation space has 367 sen-

sors and the Action space has 17 actuators.

• ArmlessHumanoid: The observation space is re-

duced to 270 sensors and the action space to 11

actuators by removing arm-related components.

The ﬁgures 2 and 3 shows pictures from the Hu-

manoid and ArmlessHumanoid simulation:

Figure 2: Visual representation of the Humanoid environ-

ment, automatically generated with Gymnasium.

This structural change in the state-action space

represents a shift beyond typical marginal distribu-

tion changes, as explained in the chapter 2. Marginal

changes can often be handled by incremental updates

or minor adjustments to the policy. However, in sce-

narios like the transition from Humanoid to Arm-

lessHumanoid, we encounter a dimensional reduction

in both the observation and action spaces, requiring a

different adaptation approach.

Figure 3: Visual representation of the ArmlessHumanoid

environment, automatically generated with Gymnaisum.

4.2 Experiment Design

The experimental design for testing ACMR involves

three primary steps to assess its adaptability in a mod-

iﬁed state-action space.

• Baseline Runs in the Source and Target En-

vironment. The teacher SAC agent A

is ﬁrst

trained in the full state-action space of the source

environment, representing the normal, unchanged

conditions (experiment H0). This baseline es-

tablishes the agent’s performance without any

state-action space reduction, serving as the per-

formance benchmark and providing the model

weights to transfer to the student SAC agent A

In addition, a baseline experiment is conducted

in the ArmlessHumanoid Environment without

ACMR, which serves as performance benchmark

for comparing the experiments (experiment A0).

• Proof of Concept in Source Environment. To

verify that ACMR correctly reuses the transferred

models, a proof-of-concept experiment is con-

ducted in the Humanoid environment with normal

state-action space (experiment H1). Here, the A

actor and critic models are transferred to the stu-

dent A

agent in the source environment without

additional modiﬁcations (not necessary since the

dimensions are the same).

• Testing Conﬁgurations. Finally, the ACMR ap-

proach is tested across the four different con-

ﬁgurations (as outlined previously) in the modi-

ﬁed environment (ArmlessHumanoid). This stage

evaluates each conﬁguration’s adaptability and ef-

ﬁciency, quantifying how well each variation ac-

celerates training and preserves learned features

from the source environment. Experiments A1,

A2, A3, A4.

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space

687

Table 2: Experiment overview for the Humanoid environ-

ment.

Experiment Environment Conﬁguration

H0 Source Baseline

H1 Source POC

A0 Target Baseline

A1 Target Conf. 1

A2 Target Conf. 2

A3 Target Conf. 3

A4 Target Conf. 4

The Table 2 provides an overview of the con-

ducted experiments.

All experiments were performed 3 times with

seeds 1, 2, and 3 to ensure the results reﬂect true

performance and are not inﬂuenced by random vari-

ations. The primary metric used was the episodic re-

turn, which represents the cumulative reward obtained

by an agent from the start to the end of each episode.

The maximum number of steps that the agent can per-

form is limited to 1,000,000, and a maximum of 1,000

steps can be performed per episode. An episode al-

ways ends when the 1,000 steps have expired or if

the agent has already failed. Average episodic returns

across all three seeds were calculated for comparative

analysis. A performance threshold of 4900 was estab-

lished based on visual inspection of performance data

from baseline experiments, representing a signiﬁcant

level consistently achieved by both baselines. To gain

deeper insights, the ’Step to Threshold’ (StT) metric

was employed, indicating the global steps required

for the agent to reach that predeﬁned performance

threshold. The agents episodic return has to reach

the threshold for ﬁve consecutive steps, minimizing

the inﬂuence of isolated outliers. Statistical analysis

involved calculating mean values and standard devi-

ations for the steps to threshold across experiments,

as well as T-scores and P-values to assess deviations

from the baseline. A P-value of less than 0.05 was

deﬁned as the signiﬁcance level, where a negative T-

score indicated that the threshold was reached earlier

than the baseline, while a positive T-score indicated it

was reached later.

The following hyper-parameters were used: A to-

tal of 1,000,000 timesteps (total timesteps) for

the experiments, a replay buffer size of 1 million

(buffer size) to store experience, and a discount

factor (gamma) of 0.99 to prioritize near-term rewards

slightly less than long-term gains. We used a target

smoothing coefﬁcient (tau) of 0.005 for stabilizing

target network updates and a batch size (batch size)

of 256 for sampling from the replay buffer. The agent

began learning after 5,000 steps (learning starts).

The learning rate of the policy network optimizer was

set to 3e-4 (policy lr), while the Q-network opti-

mizer used a rate of 1e-3 (q lr). An entropy reg-

ularization coefﬁcient (alpha) of 0.2 was applied to

encourage exploration during training.

4.3 Results

The results from the ACMR experiments are shown

below. Figure 5 shows the rolling average of episodic

returns over the global steps (total number of steps

across all episodes) for the experiments A0, A1, A2,

A3, A4, averaged over the three seed runs. And Fig-

ure 4 shows the baseline experiments H0 and A0.

The StT shown in the ﬁgures is calculated based on

the raw data, which leads to a faster reaching of the

threshold compared to the rolling average curve. The

Table 3 shows the statistical analysis of the StT.

Baseline Experiments (H0 and A0). Figure 4 shows

the rolling average of episodic returns for the baseline

experiments H0 and A0, averaged over the three seed

runs. In the background, the raw episodic return data

for seed 1 is visible, and the dashed lines indicate the

StT. The teacher agent A

in both the source and tar-

get environments achieved stable performance, estab-

lishing a benchmark that reﬂects the agent’s optimal

capability in the full state-action space. This baseline

performance serves as the comparison point for each

ACMR conﬁguration in the modiﬁed environment in

the following experiments.

Proof of Concept (H1). In the proof-of-concept ex-

periment, the direct transfer of the A

actor and critic

models without modiﬁcations in the same environ-

ment resulted in an observable jumpstart in initial per-

formance compared to standart initialization (baseline

H0), visible in ﬁgure 6. A T-score of -6.875 P-value

of 0.002 conﬁrm that the H1 is signiﬁcantly faster as

the baseline (see Table 3).

Hidden Layer Transfer (A1). By reusing only the

hidden layers, the student agent A

was able to lever-

age learned feature representations from the source

environment while adjusting the input and output lay-

ers for the modiﬁed state-action space. Only a very

small difference can be observed in a direct compar-

ison of the mean StT of A1 to the baseline A0, see

ﬁgure 5. The rolling averages are not particularly dif-

ferent either. The statistical comparison supports this

visual observation, showing no signiﬁcant difference

between the StT over the three seeds (P-value of 0.81

see Table 3).

Hidden Layer Transfer with Freezing (A2). When

freezing the transferred hidden layers, the agent A

showed an even faster adaptation time. This conﬁgu-

ration effectively preserved the learned features, re-

ducing the amount of retraining required for adap-

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

688

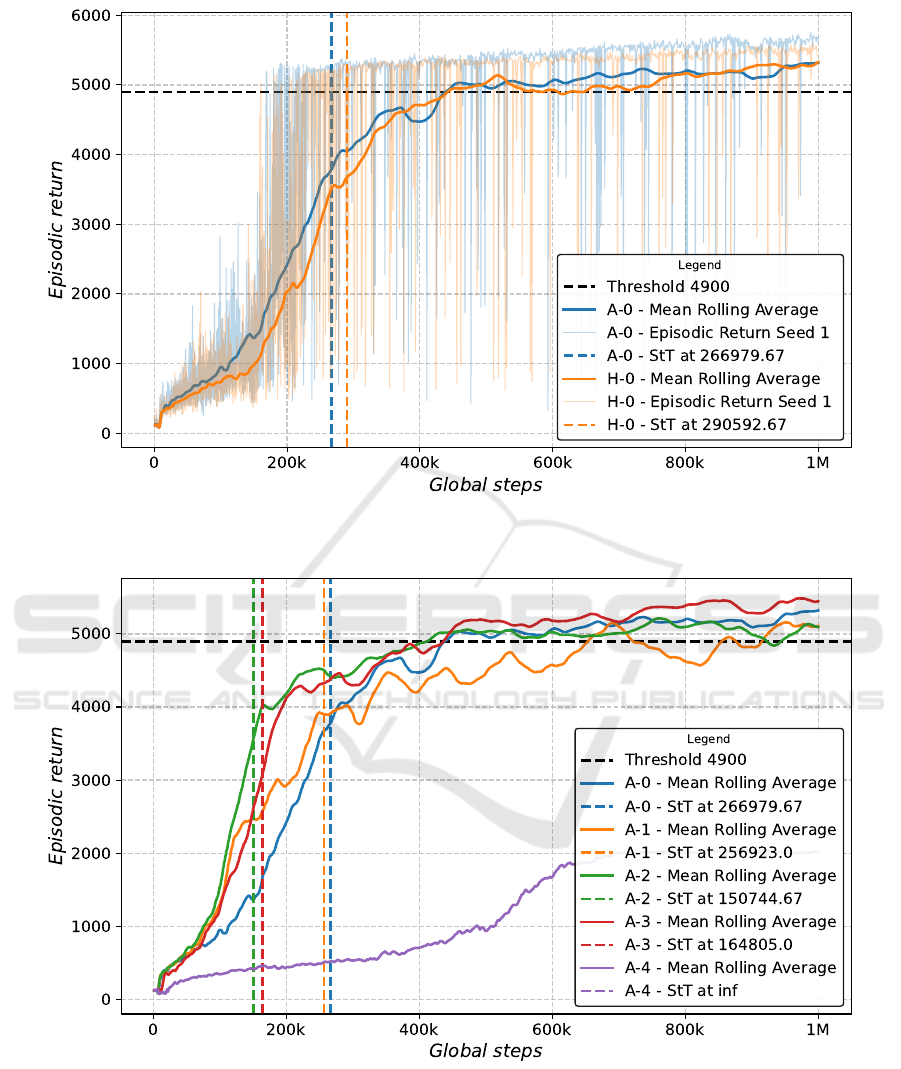
Figure 4: Comparison of baseline experiments A0 (blue) and H0 (orange) without ACMR. Rolling averages (window size

50), threshold (black), and StT (average step threshold) are shown. The background displays raw episodic returns for seed 1.

Figure 5: ACMR experiments in 4 different conﬁgurations: A0 - Baseline (blue), A1 - Hidden Layer Transfer (orange), A2 -

Hidden Layer Transfer + Freezing (green), A3 - Layer Expansion (red), A4 - Layer Expansion with Freezing (purple). Rolling

averages (window size 50), threshold (black), and StT (average step threshold) are shown.

tation. The plot shows that A2 StT outperforms the

baseline A1 StT (see Figure 5), this is also signiﬁcant

with a T-score of -4.129 and P-value of 0.015 (see Ta-

ble 3).

Layer Expansion (A3). The layer expansion ap-

proach allowed for the full transfer of the actor and

critic models with additional layers to bridge dimen-

sional differences. This conﬁguration reaches the

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space

689

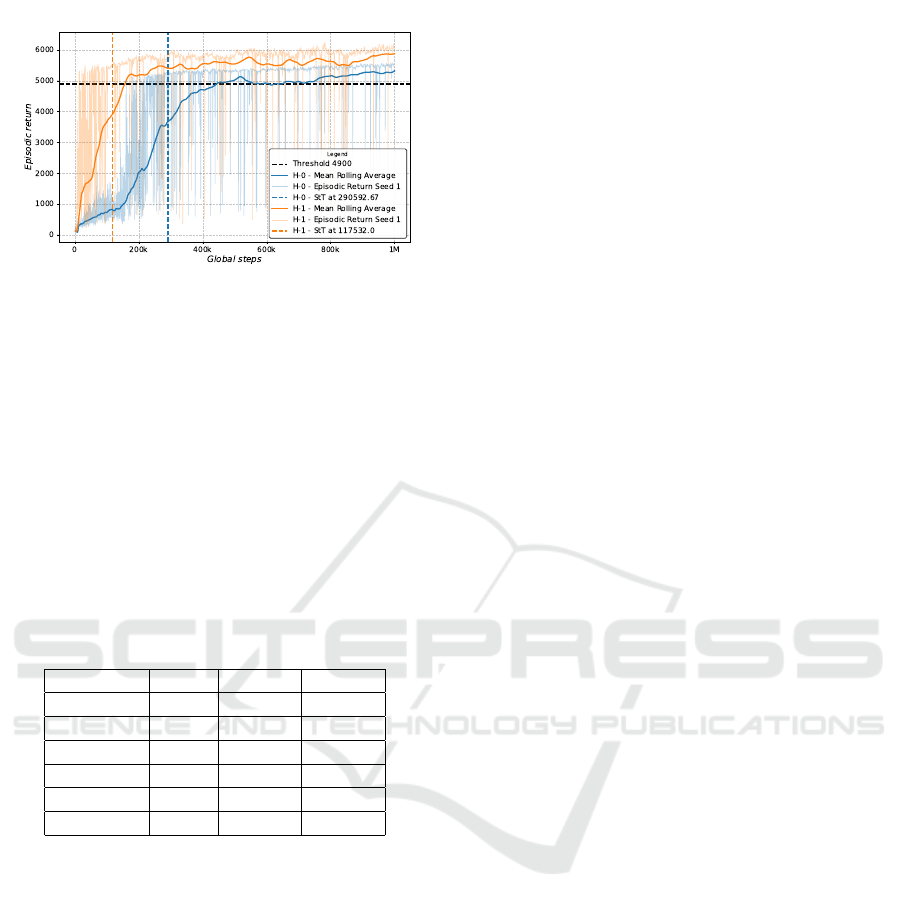
Figure 6: Proof of Concept H-0 (blue) and H-1 (orange)

with direct transfer of actor and critic models. Rolling aver-

ages (window size 50), threshold (black), and StT (average

step threshold) are shown.

threshold faster on average., see Figure 5. Which is

signiﬁcant with a T-score of -4.377 and P-value of

0.012 (see Table 3).

Layer Expansion with Freezing (A4). In the exper-

iment with ACMR conﬁguration 4, the A

agent did

not reach the threshold at all , see Figure 5. Conse-

quently, this means the agents never learned to walk

with the ArmlessHumanoid.

Table 3: Statistical comparison of average StT from all ex-

periments, including T-score and P-value calculations. The

Index is the condition being compared, and the Reference is

the baseline for comparison.

Reference Index T-score P-value

A0 A1 -0.247 0.817

A0 A2 -4.129 0.015

A0 A3 -4.377 0.012

A0 A4 NaN NaN

A0 H0 0.668 0.540

H0 H1 -6.875 0.002

In summary, the ACMR conﬁgurations ’Hidden

Layer Transfer with Freezing’ (A2) and ’Layer Ex-

pansion’ (A3), showed the most promising results,

enabling fast and effective adaptation to a modiﬁed

state-action space. These ﬁndings highlight the util-

ity of ACMR conﬁgurations in reducing training time,

underscoring their applicability in dynamic environ-

ments where rapid adaptation is crucial.

5 DISCUSSION

The experiment compared two environments: Hu-

manoid as the source domain and ArmlessHumanoid

as the target domain, with no signiﬁcant difference

in the episodic returns despite the reduction in state-

action space. A proof of concept in the source tar-

get humanoid has shown that the expected jumpstart

occurred when transferred to the same unchanged en-

vironment. This clear result was expected, as trans-

ferring a model into the same environment allows the

agent to start with knowledge from step 1M.

Experiment A1 involved only the ACMR of hid-

den layers. Although there was a slight visual indica-

tion of earlier threshold achievement, it was not sta-

tistically signiﬁcant. This suggests that hidden layer

model transfer alone does not reduce training time,

thus failing to enhance the agent’s responsiveness.

One possible explanation for this result is that the

transferred hidden layers may be direct overwritten

during subsequent training, leading to a loss of the

features learned from the source domain.

Experiment A2 achieved notable success with the

transfer of hidden layers, combined with freezing

these layers. The episodic return showed a signif-

icantly shorter training time to reach the threshold,

suggesting that freezing the transferred layers is cru-

cial. Freezing reduces noisiness in the results, likely

because it forces the agent to adjust the input and out-

put layers rather than re- learning everything.

Transferring the hidden layers as well as the orig-

inal input and output layers and then adding new in-

put and output layers for the target domain proved ef-

fective. Experiment A3 showed signiﬁcant improve-

ment in reaching the threshold. This approach al-

lows the agent to retain the primary model’s structure,

which aids in faster reward acquisition. The adapta-

tion layers works as translation layers from the cur-

rent reduced sensor and actuator count to the higher

number in the transferred model. Future research

could explore the agent’s behavior when more crucial

body parts are omitted, necessitating different walk-

ing methods.

The experiment A4 yielded unfavorable results.

The agents never reached the threshold, indicating

that the combination of freezing and additional layers

makes the agent becomes too adapted to the source

domain, leading to overﬁtting.

Thus, it indicates that effective transfer in altered

state-action spaces requires either freezing or addi-

tional layers. Too little transformed knowledge has

no effect, while too much leads to bad performance.

The conclusions drawn in this paper provide in-

sights into the optimal amount of knowledge to trans-

fer (number of transferred layers) and the extent of

behavior to ﬁx (number of frozen layers) for suc-

cessful learning acceleration. The results highlight

that a combination of extensive knowledge transfer

and ﬁxed weights and biases leads to bad perfor-

mance, but the individual application of the tech-

niques achieve excellent results. The ACMR in ex-

periment A2, i.e., the ’Hidden Layer Transfer with

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

690

Freezing’, is the best method overall. The results are

slightly better than the experiment with the ’Layer Ex-

pansion’ (A3). However, while method ’Layer Ex-

pansion’ signiﬁcantly complicates and enlarges the

neural network, Hidden Layer Transfer with Freez-

ing’ in ACMR is minimally invasive, which is another

advantage. However, this study does not explore how

the agent would respond to different changes in state-

action space that more signiﬁcantly affect walking

methodology. Moreover, only the pre-trained model

transfer methodology was reviewed, leaving other TL

methodologies to be explored.

6 CONCLUSIONS

This study demonstrates the potential of ACMR as an

effective TL method, particularly in the Hidden Layer

Transfer with Freezing (A2) and Layer Expansion

(A3) conﬁgurations, to accelerate SAC agent train-

ing in the Gymnasium Humanoid environment with

changed state-action space dimension. The A2 con-

ﬁguration was the most effective, as freezing trans-

ferred hidden layers reduced training noise and en-

abled efﬁcient adaptation to the new environment

without extensive model changes. While A3 also

achieved signiﬁcant acceleration, its added model

complexity could reduce efﬁciency in larger applica-

tions and repeated retrainings.

However, the experiments also highlighted

ACMR’s limitations. Experiment A1 (simple hidden

layer transfer) showed that transferring hidden layers

alone, without freezing, had little impact on train-

ing time, indicating that more directed knowledge

preservation is necessary. Experiment A4, which

combined layer expansion with freezing, led to bad

performance, as excessive transferred knowledge

made the agent overly speciﬁc to the source domain,

limiting its adaptability.

Overall, ACMR offers strong potential for re-

silient control in environments with changing state-

action spaces by enabling rapid adaptation.

7 FUTURE WORK

The results presented in this paper pave the way

for further research in TL for evolving state-action

spaces, with signiﬁcant potential for advancing the

ﬁeld, particularly through the use of ACMR. Future

studies should explore ACMR in more complex en-

vironments and investigate variations in state-action

spaces, comparing its performance with other TL

methods. A key area of focus will be the application

of ACMR in real-world environments, such as power

grids. Speciﬁcally, ACMR will be integrated into the

ARL methodology (Fischer et al., 2019) for resilient

control of power grids, with the goal of enhancing

the responsiveness of learning agents to unforeseen

changes (Veith et al., 2024).

ACKNOWLEDGEMENTS

This research was supported by funding from the

German Federal Ministry of Education and Research

(BMBF) under Grant No. 01IS22047C. We extend

our gratitude to ChatGPT, an AI model developed by

OpenAI, for assistance with language reﬁnement and

corrections. Special thanks go to Thomas Wolgast

and Torben Logemann for their thorough internal re-

view, as well as to all our colleagues for their invalu-

able discussions and support throughout this work.

REFERENCES

Amodei, D., Olah, C., Steinhardt, J., Christiano, P., Schul-

man, J., and Mane, D. (2018). Ai and compute. Ope-

nAI Blog, 8(7):1–9.

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and

Bharath, A. A. (2017). Deep reinforcement learning:

A brief survey. IEEE Signal Processing Magazine,

34(6):26–38.

Barg, F. M. (2024). Actor-critic model reuse for transfer

learning in humanoid environments. https://github.

com/feline-malin/ACMR for Humanoid.

Beck, N., Rajasekharan, A., and Tran, H. (2022).

Transfer reinforcement learning for differing action

spaces via q-network representations. arXiv preprint

arXiv:2202.02442.

Celiberto Jr, L. A., Matsuura, J. P., De M

antaras, R. L.,

and Bianchi, R. A. (2010). Using transfer learning to

speed-up reinforcement learning: a cased-based ap-

proach. In 2010 latin american robotics symposium

and intelligent robotics meeting, pages 55–60. IEEE.

Fern

andez, F. and Veloso, M. (2006a). Policy reuse for

transfer learning across tasks with different state and

action spaces. In ICML Workshop on Structural

Knowledge Transfer for Machine Learning. Citeseer.

Fern

andez, F. and Veloso, M. (2006b). Probabilistic policy

reuse in a reinforcement learning agent. In Proceed-

ings of the ﬁfth international joint conference on Au-

tonomous agents and multiagent systems, pages 720–

727.

Fischer, L., Memmen, J. M., Veith, E. M., and Tr

oschel,

M. (2019). Adversarial resilience learning—towards

systemic vulnerability analysis for large and complex

systems. In ENERGY 2019, The Ninth International

Conference on Smart Grids, Green Communications

Transfer Learning in Deep Reinforcement Learning: Actor-Critic Model Reuse for Changed State-Action Space

691

and IT Energy-aware Technologies, number 9, pages

24–32, Athens, Greece. IARIA XPS Press.

Ganin, Y., Ustinova, E., Ajakan, H., Germain, P.,

Larochelle, H., Laviolette, F., March, M., and Lem-

pitsky, V. (2016). Domain-adversarial training of neu-

ral networks. Journal of machine learning research,

17(59):1–35.

Haarnoja, T., Zhou, A., Abbeel, P., and Levine, S. (2018).

Soft actor-critic: Off-policy maximum entropy deep

reinforcement learning with a stochastic actor. In

International conference on machine learning, pages

1861–1870. PMLR.

Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup,

D., and Meger, D. (2018). Deep reinforcement learn-

ing that matters. In Proceedings of the AAAI confer-

ence on artiﬁcial intelligence, volume 32.

Kumar, A., Zhou, A., Tucker, G., and Levine, S. (2020).

Conservative q-learning for ofﬂine reinforcement

learning. Advances in Neural Information Processing

Systems, 33:1179–1191.

Nair, A., McGrew, B., Andrychowicz, M., Zaremba, W.,

and Abbeel, P. (2018). Overcoming exploration in re-

inforcement learning with demonstrations. In 2018

IEEE international conference on robotics and au-

tomation (ICRA), pages 6292–6299. IEEE.

Nguyen, T. T., Nguyen, N. D., and Nahavandi, S. (2020).

Deep reinforcement learning for multiagent systems:

A review of challenges, solutions, and applications.

IEEE transactions on cybernetics, 50(9):3826–3839.

Omitaomu, O. A. and Niu, H. (2021). Artiﬁcial intelligence

techniques in smart grid: A survey. Smart Cities,

4(2):548–568.

Pan, S. J. and Yang, Q. (2010). A survey on transfer learn-

ing. IEEE Transactions on knowledge and data engi-

neering, 22(10):1345–1359.

Parisotto, E., Ba, J. L., and Salakhutdinov, R. (2015). Actor-

mimic: Deep multitask and transfer reinforcement

learning. arXiv preprint arXiv:1511.06342.

Tan, M., Tian, A., and Denoyer, L. (2022). Regularized

soft actor-critic for behavior transfer learning. In 2022

IEEE Conference on Games (CoG), pages 516–519.

IEEE.

Taylor, M. E. and Stone, P. (2009). Transfer learning for

reinforcement learning domains: A survey. Journal of

Machine Learning Research, 10(7).

Towers, M., Kwiatkowski, A., Terry, J., Balis, J. U.,

De Cola, G., Deleu, T., Goul

ao, M., Kallinteris, A.,

Krimmel, M., KG, A., et al. (2024). Gymnasium: A

standard interface for reinforcement learning environ-

ments. arXiv preprint arXiv:2407.17032.

Veith, E. M., Logemann, T., Wellßow, A., and Balduin, S.

(2024). Play with me: Towards explaining the beneﬁts

of autocurriculum training of learning agents. In 2024

IEEE PES Innovative Smart Grid Technologies Eu-

rope (ISGT EUROPE), pages 1–5, Dubrovnik, Croa-

tia. IEEE.

vwxyzjn (2024). sac continuous action.py. https://github.

com/vwxyzjn/cleanrl/blob/master/cleanrl. Accessed:

2024-05-28.

Weiss, K., Khoshgoftaar, T. M., and Wang, D. (2016).

A survey of transfer learning. Journal of Big data,

3(1):1–40.

Wolgast, T. and Nieße, A. (2024). Learning the opti-

mal power ﬂow: Environment design matters. arXiv

preprint arXiv:2403.17831.

Xu, Z., Yang, D., Tang, J., Tang, Y., Yuan, T., Wang,

Y., and Xue, G. (2020). An actor-critic-based trans-

fer learning framework for experience-driven net-

working. IEEE/ACM Transactions on Networking,

29(1):360–371.

Zhu, Z., Lin, K., Jain, A. K., and Zhou, J. (2023). Trans-

fer learning in deep reinforcement learning: A survey.

IEEE Transactions on Pattern Analysis and Machine

Intelligence.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

692