Portfolio Optimization Based on Prospect Theory

Celma de Oliveira Ribeiro

and Alan Teixeira dos Santos

Department of Industrial Engineering, Polytechnic School of the University of Sao Paulo,

Av. Prof. Luciano Gualberto, 380 - Butanta, Sao Paulo, Brazil

{celma, alantds}@usp.br

Keywords:

Prospect Theory, Portfolio Optimization, Decision-Making.

Abstract:

This paper investigates the application of prospect theory in the context of portfolio optimization and presents

a model based on the mean absolute deviation and on Prospect Theory. By analyzing historical returns from as-

sets of three critical sectors traded on B3 (Brazilian Stock Exchange) and over an eight-year period, a prospect

optimization approach was implemented and its results were compared to those obtained from the Conditional

Value at Risk (CVaR) approach. An additional application was held regarding one of the most relevant sector

of assets in terms of contribution to the S&P500’s composition with the purpose to test the new model under

different market conditions. Such results revealed the effectiveness of prospect theory in optimizing portfolios

since those results were considered similar to the CVaR’s, but at higher returns. Both models were compared

through different portfolio performance metrics and, notably, the prospect model exhibited competitive results

in most cases. However, the study also identiﬁed opportunities for further reﬁnements. Overall conclusions

herein suggests the promise of prospect theory in addressing the needs of decision makers in portfolio manage-

ment, delivering a singular approach that balances the possibility of gains and losses under different scenarios.

1 INTRODUCTION

In the early 1950s, (Markowitz, 1952) contradicted

the thesis that investors should maximize or anticipate

expected returns and stated that investors should con-

sider the expected return as something desirable and

the variance as something undesirable. Markowitz de-

veloped an optimization model to minimize the port-

folio risk, considering the variance of portfolio returns

as the risk measure, subjected to an expected return,

which resulted in a quadratic optimization model.

Moreover, Markowitz presented the concept of ef-

ﬁcient frontier for portfolios, and his contributions

are considered the basis of Modern Portfolio Theory

(MPT).

Since Markowitz’s contribution, subsequent re-

searches have been published with the purpose of de-

veloping new approaches for portfolios or reducing

the computational cost in obtaining the solution for

the optimization problem.

A few decades later, (Konno and Yamazaki, 1991)

analyzed Markowitz’s model and replaced the vari-

ance - the second moment of probability distribution

of portfolio returns, by the mean absolute deviation

https://orcid.org/0000-0003-0288-2644

https://orcid.org/0009-0005-9435-1948

(MAD) - the ﬁrst moment of probability distribution

of portfolio returns, with the intent of reducing the

computational time of the quadratic model.

The variance and the mean absolute deviation are

statistical measures traditionally applied in the con-

text of portfolio problems. However, these measures

cannot identify the anomalies in the probability distri-

bution of portfolio returns nor the extent of potential

losses in a given portfolio. Thus, in the mid-1990s,

the concept of Value at Risk (VaR) (Group of Thirty,

1993) was proposed in the JP Morgan G30 publica-

tion.

The VaR is deﬁned by (Jorion, 2006) as the maxi-

mum loss of a portfolio under ordinary market condi-

tions and at a given conﬁdence level. VaR is therefore

related to the percentiles of the probability distribu-

tion of the losses at a predetermined conﬁdence level.

Recognized as a metric for risk, VaR has become a

widely useful tool for the ﬁnancial market and also an

important regulatory measure.

Despite being widely disseminated, VaR has been

considered unsuitable when losses do not follow a

normal distribution, which occurs in most cases. Of-

ten, the probability distributions of returns exhibit

”heavy tails”, making VaR inefﬁcient for identifying

extreme risks. In that context, (Rockafellar and Urya-

sev, 2002) stated that due to the fact that VaR does not

Ribeiro, C. O. and Santos, A. T.

Portfolio Optimization Based on Prospect Theory.

DOI: 10.5220/0013331900003956

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 7th International Conference on Finance, Economics, Management and IT Business (FEMIB 2025), pages 51-60

ISBN: 978-989-758-748-1; ISSN: 2184-5891

evaluate losses that exceed the predetermined conﬁ-

dence level, it may show an optimistic tendency rather

than a conservative one, which should prevail in risk

management.

In 2000’s a new risk measure called Conditional

Value at Risk (CVaR) was proposed by (Rockafellar

and Uryasev, 2000). CVaR is the average of the ex-

pected returns that exceed VaR’s for a given conﬁ-

dence level. CVaR consists of the expectancy of the

tail values of the probability distribution that repre-

sent the worst-case return scenarios (Rockafellar and

Uryasev, 2000). Accordingly, CVaR is able to mea-

sure the ”tail losses” under a more robust approach.

Additionally, CVaR exhibits superior properties com-

pared to VaR, since (Artzner et al., 1999) stated that

CVaR can be considered as a coherent risk measure by

having a group of properties which includes subaddi-

tivity: CVaR

+ R

) ≤ CVaR

) + CVaR

)

- that is a property that VaR does not meet.

The objective functions comprehended in op-

timization problems originated from MPT can be

placed within the concept of utility functions, espe-

cially since the predominance of Utility Theory as the

main method of decision-making under uncertainty at

that time. Utility Theory is based on the assumption

of the rational investor, and has served as the primary

lens through which the behavior of economic agents

has been interpreted. However, an alternative method

has been disseminated in decision-making analysis

since (Kahneman and Tversky, 1979). That paper in-

troduced Prospect Theory, fundamentally altering the

decision-making analysis by demonstrating that peo-

ple weight losses more heavily than gains in general

situations, contradicting the assumption of the ratio-

nal investor.

Prospect Theory diverges from Utility Theory by

considering that decisions are affected by other bi-

ases instead of the assumption taken in the con-

cept of rational investor. (Kahneman and Tversky,

1979) posited that the value function in Prospect The-

ory is characterized by a deviation from a reference

point, exhibiting concavity for gains and convexity

for losses and having greater weight on the convex

part than on the concave one. Further reﬁnements by

(Kahneman and Tversky, 1992) incorporated nonlin-

ear preferences, a concept of loss aversion and a cu-

mulative function which allows applications for con-

tinuous variables.

Other researches in the literature have tested the

effectiveness of Prospect Theory in explaining in-

vestor behavior, as well as in explaining portfolio re-

turns or even in understanding market tendencies.

Subsequent researches have extensively tested the

applicability of Prospect Theory in explaining in-

vestor behavior and portfolio returns across various

market sectors. For instance, (Benartzi and Thaler,

1995) examined the equity premium puzzle — why

American stocks outperformed bonds throughout the

20th century — by presenting two main arguments.

The ﬁrst argument is based on Prospect Theory, as-

serting that investors are more sensitive to losses than

to gains. In other words, investors tend to treat the

possibility of losses more severely and seek greater

possibilities of gains. The second argument addresses

a distinct concept known as ”myopic loss aversion”,

which means that people tend to show more con-

cern about their portfolios in a short-period and do

not show the same concern for long-term results.

The paper presented a piecewise linear optimization

model accordingly and the results deﬁned a period

of investor’s indifference towards their portfolios that

proper justiﬁed the “equity premium puzzle” from the

authors’ perspective.

Further studies, such as those by (Benartzi and

Thaler, 1995) and (Barberis et al., 2001) have demon-

strated that asset prices that were inﬂuenced by loss

aversion were closely aligned with historical data

while showed minimal correlation with consumption

growth. The broad dissemination of Prospect Theory

inﬂuenced (Barberis and Thaler, 2003) to critique and

highlight the theoretical distinctions between rational

and non-rational investor proﬁles, identifying chal-

lenges in arbitrage limits and noting a lack of practical

applications at that time.

A few years later, (De Giorgi et al., 2010) argued

that the ﬁnancial market would not need to adopt the

equilibrium hypotheses if agents had heterogeneous

preferences in accordance with Cumulative Prospect

Theory (Kahneman and Tversky, 1992). The paper

contradicted traditional ﬁnancial models in which this

concept of equilibrium was fundamental.

Speciﬁcally in portfolio problems, Prospect The-

ory has been applied as an alternative approach to

explain returns, risk and the overall decision-making

by investors in different scenarios. (Best and Grauer,

2016) proposed a multi-period problem for maximiz-

ing returns, in which the concept of loss aversion was

applied and the loss aversion coefﬁcient from (Kahne-

man and Tversky, 1992) was used in a portfolio with

different assets and rates. The paper also considers

the concept of kink, that is the non-differentiable seg-

ment that connects the gain-curve to the loss-curve of

the Prospect Theory’s value function. Relevant op-

portunities in optimization have arisen regarding the

concept of kink. There has been particular interest in

this application, specially by the fact it has been quite

challenging. (Best and Zhang, 2011) and (Best et al.,

2014) are examples of this application.

FEMIB 2025 - 7th International Conference on Finance, Economics, Management and IT Business

(Best and Grauer, 2017) compared three port-

folio optimization approaches—power utility, mean-

variance, and prospect theory—analyzing static and

dynamic contexts with varying borrowing and lend-

ing rates. The paper showed that the prospect theory

model performed well for risk aversion coefﬁcients

between 2 and 2.25, but results were considered in-

consistent otherwise. The power utility and mean-

variance models performed reasonably for risk-averse

investors, though less risk-averse ones relied heavily

on borrowing.

(Wang et al., 2021) applied Prospect Theory to

analyze the behavior of Chinese investors during an

external regulatory shock. The study concluded that

Prospect Theory had a strong predictive power to ex-

plain stock returns, particularly for small-cap compa-

nies, with the theory effectively explaining investor

decision-making.

(Zhong et al., 2022) proposed the ”Three-way de-

cision model”, an optimization approach based on

Prospect Theory that addresses challenges of time and

monetary variables. The model delivered three out-

comes as options to the investor: ”accept”, ”reject”,

or ”not accept nor reject”, and it aimed to maximize

monetary value while the variable time was also taken

into account. Finally, some improvements were sug-

gested, particularly when treating monetary outcomes

and time as independent variables, which does not

necessarily happen. The authors also noted that cer-

tain model parameters require reﬁnement.

Fostering the discussion of decision-making under

risk, Prospect Theory has been increasingly applied

to different ﬁelds with diverse objectives. This pa-

per therefore seeks to contribute to further advancing

by leveraging Prospect Theory as a decision-making

method through a particular application to portfolio

problems. This approach consists in a new optimiza-

tion model developed from the mean absolute devi-

ation (Konno and Yamazaki, 1991) in addition with

concepts from Prospect Theory.

Studies in literature that consider Prospect The-

ory in the context of portfolio optimization, have pro-

vided comparisons with the classic Portfolio Theory

(Markowitz, 1952), that is the case of (Pﬁffelmann

et al., 2016). However, a few applications were pre-

sented regarding other risk measures. Therefore, this

paper provides a comparison of the new optimization

model proposed along with Conditional Value at Risk

(CVaR) (Rockafellar and Uryasev, 2000), under dif-

ferent conﬁdence levels.

The methodology herein provides a contribution

to portfolio optimization, specially on the applica-

tion of prospect theory as a framework for decision-

making under risk, justiﬁed by the development of a

new optimization model which is compared against

the traditional CVaR model. Additionally, the mathe-

matical approach developed utilizes two linearization

techniques, the ﬁrst one is based on (J

udice et al.,

2003), where auxiliary variables were applied on the

model and the second one, was presented in (Asghari

et al., 2022) since the function has non-linear terms

comprehended in the piecewise function.

The paper is structured, as: Section 2 presents the

new optimization model and elaborates the methodol-

ogy. Section 3 provides an analytical comparison of

the portfolio models, presents the results and elabo-

rates an argumentative discussion about these results.

Section 4 provides concluding remarks and identiﬁes

potential opportunities for further researches.

2 PORTFOLIO OPTIMIZATION

MODEL

In this paper, a new approach is presented based on

Prospect Theory and on the mean absolute deviation,

that was linearized in accordance with (J

udice et al.,

2003). Firstly, a new risk measure is introduced where

potential losses grow non-linearly by being weighted

by two different coefﬁcients. For potential portfolio

gains, just one coefﬁcient is applied.

Consider positive real numbers ζ, β

. . . β

with

0 < ζ ≤ β

≤ β

≤ . . . ≤ β

. Let w ∈ R

be the portfo-

lio composition with u ∈ R. The proposed risk mea-

sure is an extension of MAD, given as:

f (u, w) =

(

ζu if u

≥ 0

u if d

i−1

≤ u

−

≤ d

i ∈ {1 . . . I}

(1)

with:

≤ d

< d

as negative real numbers

As posited in Prospect Theory, the investor gen-

erally weights losses more heavily than gains and

therefore, the risk measure should reproduce this re-

lation. Moreover, the risk measure emulates two sce-

narios for potential losses, one more severe so that it

is weighted more heavily than the another. This con-

dition produces a piecewise linear function compre-

hended by two functions with different slopes.

Assume u = u

−u

−

, u

≥ 0 and u

−

≥ 0. Due

to the complementary conditions u

·u

−

= 0 and c

−d

i ∈ {1 . . . I}, f (u, w) can be rewritten as:

Portfolio Optimization Based on Prospect Theory

f (u, w) =

(

ζu

if u

≥ 0

−

if c

i−1

≤ −u

−

≤ c

i ∈ {1 . . . I}

(2)

As observed, f (u, w) is a piecewise linear function

with c

≤ c

being the breakpoints for the

function.

Let consider:

g(u

−

) =

−

if c

i−1

≤ −u

−

≤ c

i ∈ {1 . . . I}

(3)

Adopting the approach of (Asghari et al., 2022),

consider Y

∈ {0, 1} i ∈ {1 . . . I} so that

∑

= 1 and

= Y

· g(u

−

) be the auxiliary variables. It is easy to

verify that:

f (u, w) =

∑

+ ζ · u

(4)

subject to:

∑

i=1

i−1

≤ u

−

≤

∑

i=1

(5)

∑

i=1

= 1 (6)

g(u

−

) − (1 −Y

)M ≤ z

∀t ∈ {1 . . . T } (7)

g(u

−

) + (1 −Y

)M ≥ z

∀t ∈ {1 . . . T } (8)

−Y

M ≤ z

≤ Y

M ∀t ∈ {1 . . . T } (9)

∈ {0, 1}, j = 1 . . . n (10)

∈ R (11)

Based on this framework, let introduce the param-

eter V

∗

as the breakpoint of the function g(u

−

) and,

in theoretical terms, the kink as postulated by Prospect

Theory.

Let t ∈ {1, . . . , T } denote the time horizon and let

revisit (J

udice et al., 2003), where the mean abso-

lute deviation (MAD) model was linearized as φ(u) =

∑

t=1



+ u

−



. By the complementary condition

· u

−

= 0, and through the relation in u

− u

−

∑

j=1

−

, ∀t ∈ {1, . . . , T }, a fundamental

part of the constraints set in the reformulated opti-

mization model is deﬁned.

Let M be a sufﬁciently large number to bound the

auxiliary variables z

= Y

· g(u

−

). This adjustment is

necessary since g(u

−

) has been reallocated to the con-

straint set, while z

remains in the objective function,

according to the process of linearization.

Consequently, the reformulated optimization

model, introducing a new risk measure in the objec-

tive function, is now expressed as follows:

Minimize

(w,u,z)

Ψ(u, z) =

∑

t=1

(ζu

) +

∑

t=1

∑

i=1

)

(12)

subject to:

w =











w ∈ R



∑

j=1

= 1;

∑

j=1

≥ R

;

≥ 0, ∀ j ∈ {1 . . . n}











(13)

∗

≤ u

−

≤ V

∗

+ MY

(14)

∑

= 1 (15)

g(u

−

) − (1 −Y

)M ≤ z

∀t ∈ {1 . . . T } (16)

g(u

−

) + (1 −Y

)M ≥ z

∀t ∈ {1 . . . T } (17)

−Y

M ≤ z

≤ Y

M ∀t ∈ {1 . . . T } (18)

− u

−

∑

j=1

− R

∀t . . . T (19)

M ∈ R, z

∈ R

∈ {0, 1}, j = 1 . . . 10

, u

−

≥ 0

0 < ζ < β

< β

, t ∈ {1 . . . T }

Where:

is the historical return of asset j with j = 1. . . n

in the period t with t = 1 . . . T .

is the percentage allocated to asset j.

is the average return of asset j.

is the minimum return required by the investor.

M is a sufﬁciently large real number.

, . . .Y

are binary variables responsible for

the assignment of the expressions in g(u

−

FEMIB 2025 - 7th International Conference on Finance, Economics, Management and IT Business

i corresponds to the set of equations of the piece-

wise linear function with i = 1. . . I and, in this case,

with I = 2.

are the auxiliary variables.

∗

is a parameter based on the idea of the kink

arising from Prospect Theory and its value denote in

which expression of g(u

−

) the variable u

−

lies on.

Observe that this is a mixed-integer programming

model in which the number of binary variables does

not depend on the number of observations of the time

series.

In the model, the Equation (12) is the objec-

tive function that minimizes the total portfolio risk,

weighting differently gains and losses. Equation (13)

is the set of constraints deﬁned in Markowitz’s model.

Equation (14) represents the domain of u

−

, i.e., the

lower and upper limits for u

−

in each expression, re-

spectively. Equation (15) ensures the characteristic of

the variables as binary type. Equations (16) to (18)

establish a lower and upper bound for z

. Equation

(19) establishes an exact relationship between the dif-

ference of returns above and below the average.

The prospect model composed by a new risk mea-

sure turned the piecewise linear function into a lin-

ear function and consequently the model into a Linear

Programming (LP) problem which is less complex in

terms of computational time.

2.1 Portfolio Assessment

The performance of each portfolio optimization

model is measured through the set of metrics based

on (Ramos et al., 2023). These metrics are described

as follows.

The volatility of the portfolio returns can be mea-

sured through the standard deviation. With respect to

the negative deviations, that comprehends the portfo-

lio returns below the expected returns, the metric used

is the semi-deviation. These metrics can be expressed

as follows:

σ =

E [(R − E[R])

] (20)

−

E[((R − E[R])

−

)

] (21)

Where: E[R] is the expected return of the portfo-

lio.

While standard deviation σ denotes the portfolio

risk, semi-deviation denotes only the deviations be-

low the expected returns of the portfolio (Ramos et al.,

2023).

The traditional VaR is used considering the histor-

ical returns, or in other words, it considers the non-

parametric approach.

VaR

(w) = −Q

∑

j=1

(22)

The signiﬁcance level considered is 95%, quite

common in the literature.

The widely known Sharpe Ratio consists of the

excess-return ratio per the standard deviation and

measures the portfolio performance.

Sharpe =

E[R − r

]

(23)

Where: r

is the risk-free rate.

In (Sortino and Satchell, 2001) , the standard de-

viation contained in the Sharpe Ratio’s formula is re-

placed by the Semi Deviation Sd

−

, comprehending

therefore the negative deviations.

Sortino =

E[R − r

]

−

(24)

The STARR Ratio is another metric utilized and

it is the expected excess of portfolio returns per the

CVaR of the excess of portfolio returns. STARR Ratio

also derives from Sharpe Ratio, but takes into account

the reward for each CVaR’s value and is therefore

considered a tail-risk-reward (Ramos et al., 2023). An

example of such approach can be found in (Mainik

et al., 2015).

STARR =

E[R − r

]

CVaR

(R − r

)

(25)

For the methodology of Systematic Risk, an ap-

proach similar to (Ramos et al., 2023) is adopted

where a coefﬁcient β is used and obtained through

the Ordinary Least Squares (OLS) Regression, such

as follows:

E[R] = r

+ β(E[B] − r

) + ε (26)

where:

is the risk-free rate.

(E[B] − r

) is the excess return (market risk pre-

mium), where E[B] is the benchmark return (IBOV in-

dex for the Brazilian study and S&P500 for the Amer-

ican study, both presented herein).

β is the coefﬁcient of the regression or in better

words, the sensibility of the portfolio to the market

risk premium.

ε is an error considered.

Additionally, β’s results represent the sensibility

of the portfolio returns to the market risk premium

Portfolio Optimization Based on Prospect Theory

so that returns above and below the expected mar-

ket returns are commonly called bull or bear mar-

ket and therefore, were called β

(+)

and β

(−)

, respec-

tively. The Brazilian benchmark index adopted was

the IBOV for the Brazilian application and S&P500

for the American’s.

3 RESULTS

3.1 Data and Application

The application of the methodology previously dis-

cussed considered three pivotal sectors from the

Brazilian Stock Exchange (Brasil, Bolsa, Balc

ao -

(B3, 2025)). These sectors were: Oil & Gas, Finan-

cial/Banking, and Electricity sector. A total of 27 as-

sets were chosen, comprising 7 from the Oil & Gas

and 10 from each of the remaining sectors. The selec-

tion criteria prioritized assets with historical returns

that cover all time horizon and focused on prominent

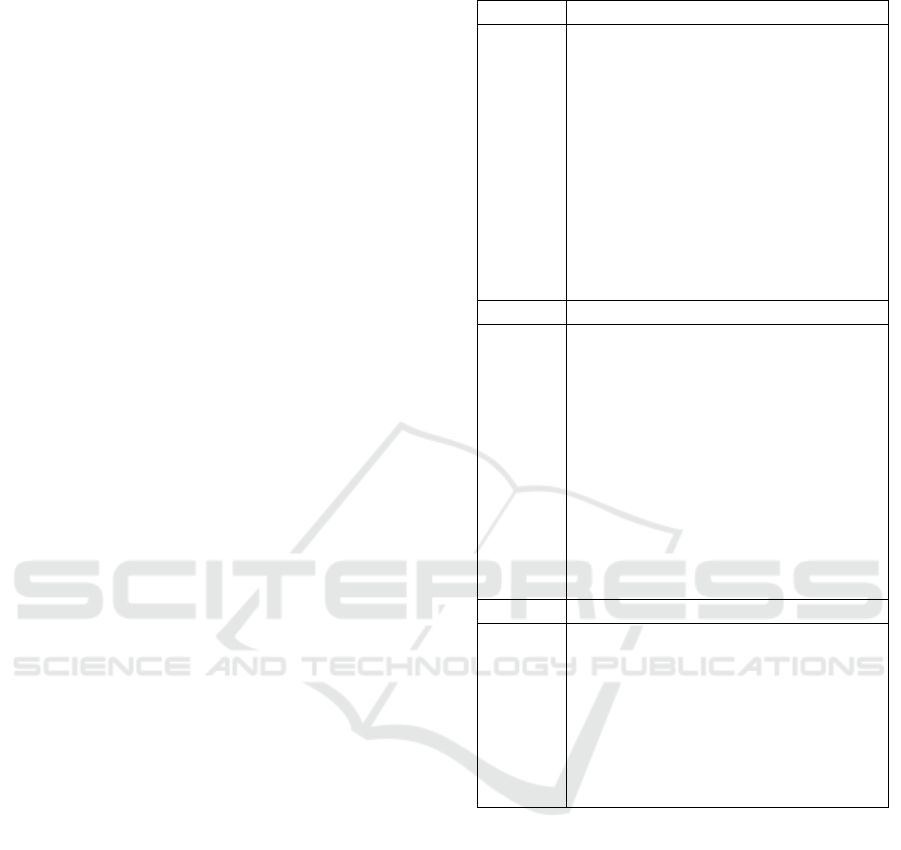
Brazilian companies. Observe in Table 1 the set of

assets belonging to each of the sectors considered.

These sectors also were selected due to their sub-

stantial inﬂuence on the ﬂuctuations of IBOV. This in-

dex is also utilized as a reference in one of the metrics

previously detailed.

Analogously, an additional application was held

to test the methodology proposed herein under dif-

ferent market conditions. Therefore, an important

sector from the American stock market was selected

to run both models under the same method, criteria

and period. The sector selected was Technology with

10 stocks from the most valuable companies open in

Nasdaq (American Exchange), as shown in Table 2.

The analysis for both studies spans approximately

eight years, from January 2015 to December 2023,

justiﬁed not only for its duration but also for encom-

passing the COVID-19 pandemic, a period of consid-

erable volatility to the portfolio returns. This time

horizon with some instability is critical for testing the

robustness of the proposed portfolio model.

In order to consider a balanced temporal dynam-

ics, the eight-years period was subdivided into mov-

ing windows, as proposed by (Best and Grauer, 2016).

This approach facilitates the identiﬁcation of trends

and documents performance variations across these

periods within the time horizon. Each window spans

the same number of 319 days, ensuring consistency in

temporal analysis.

The application is conducted for two portfolio op-

timization problems: the CVaR optimization model

and the newly prospect optimization model, derived

from mean absolute deviation (MAD) and Prospect

Table 1: Companies By Sector - B3-Brazil.

Code Electricity

CPLE3 Cia Paranaense De Energia-Copel

CMIG3 Cia Energ

etica De Minas Gerais-

Cemig

ELET3 Centrais Elet Bras S.A-Eletrobras

CPFE3 Cpﬂ Energia S.A

LIGT3 Light S.A.

EQTL3 Equatorial Energia S.A

EGIE3 Engie Brasil Energia S.A

ENGI11 Energisa S.A.

CSLC3 Centrais Elet De Santa Catarina S.A

TAEE11 Transmissora Alianc¸a de En. El

etrica

S.A

Code Banking/Financial

BPAN4 Banco Pan S.A

BEES3 Banestes S.A-Banco do E. do E.

Santo

BRSR6 Banrisul S.A-Banco do E. do R. G.

Do Sul

BBDC4 Banco Bradesco S.A

BBAS3 Banco Brasil S.A

BAZA3 Banco Amaz

onia S.A

ITUB4 Ita

u Unibanco Holding S.A

BMEB4 Banco Mercantil Do Brasil S.A

BNBR3 Banco Nordeste Do Brasil S.A

SANB11 Bco Santander (Brasil) S.A

Code Oil & Gas

ENAT3 Enauta Participac¸

oes S.A

RPMG3 Reﬁnaria De Petr

oleos Manguinhos

S.A.

PETR3 Petr

oleo Brasileiro S.A - Petrobras

PRIO3 Petro Rio S.A

UGPA3 Ultrapar Participac¸

oes S.A

LUPA3 Lupatech S.A

OSXB3 Osx Brasil S.A

Theory. The CVaR problem is assessed across a few

conﬁdence levels, whereas the prospect optimization

model is assessed under different weighting parame-

ters.

Each optimization model and sector was analyzed

with respect to risk, return, and with respect to the

portfolio assessment metrics described herein. The

time horizon was divided into seven moving windows

across the three selected sectors.

The CVaR is evaluated under a few conﬁdence

levels, that are 90%, 95% and 99% whereas the

prospect model was evaluated under a group of a few

parameters, based on Prospect Theory and being sub-

divided into 9 problems, as shown on the next table.

The variations in the coefﬁcients of the Prospect

Optimization Model were designed to assess the

model under different gains and losses scenarios, con-

FEMIB 2025 - 7th International Conference on Finance, Economics, Management and IT Business

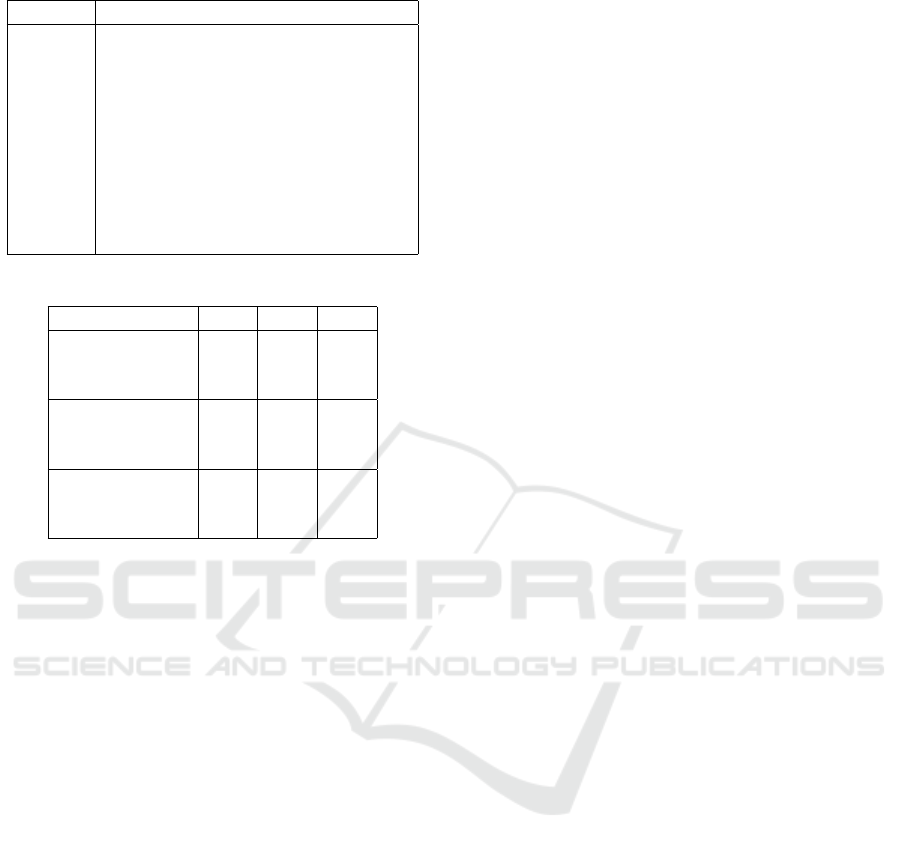
Table 2: Companies By Sector - Nasdaq-USA.

Code Technology

AAPL Apple Inc.

MSFT Microsoft Corporation.

NVDA NVIDIA Corporation.

AMZN Amazon.com Inc.

GOOGL Alphabet Inc.

META Meta Platforms Inc.

TSLA Tesla Inc.

AVGO Broadcom Inc.

CSCO Cisco Systems, Inc.

ADBE Adobe Inc.

Table 3: Parameters for each Prospect model.

Prospect Model ζ β

Prospect 1.1 1.10 0.50 1.25

Prospect 1.2 1.10 0.50 2.25

Prospect 1.3 1.10 0.50 3.25

Prospect 2.1 1.10 1.50 1.25

Prospect 2.2 1.10 1.50 2.25

Prospect 2.3 1.10 1.50 3.25

Prospect 3.1 1.10 2.50 1.25

Prospect 3.2 1.10 2.50 2.25

Prospect 3.3 1.10 2.50 3.25

trasting with CVaR performance, and both of their

performances evaluated by the deﬁned portfolio met-

rics.

The parameter V

∗

, which is based on the idea of

the kink, was quantiﬁed as an average of the CVaR’s

results.

The results for the metrics mentioned are pre-

sented along three tables speciﬁcally for each sector,

but considering the whole time series. The full pe-

riod was applied for a matter of enough data to calcu-

late the portfolio performance metrics and to organize

a reasonable comparison. Each metric is compared

separately in each column of each table. Therefore,

colors in green represent positive results to a speciﬁc

metric in a column from each table. Colors in red

mean negative results. Colors in yellow mean inter-

mediate results. Occasional column with only yel-

low results means that the results are too close to each

other so that they are all considered intermediate.

3.2 Discussion

The performance of the models for the Brazilian case

is exhibited in Table 4, which contains results for the

electricity sector and in Tables 5 and 6, which con-

tain results for the Financial and the Oil & Gas sector,

respectively.

The Table 4 exhibited properties of higher risk for

prospect models with exception to CVaR 90%. No-

tably, the standard deviation σ and the semi-deviation

Sd(−) are higher along this period demonstrating

higher volatility of portfolio returns. When recheck-

ing the data, it was concluded that there were con-

siderable losses within that period, and it was con-

ﬁrmed through the analysis of the index of electric-

ity of this sector (B3-IEE, 2025). The exception oc-

curred for VaR, in which prospect model achieved low

risk. With respect to the reward-risk metrics, Sharpe,

Sortino and STARR, CVaR’s models produced a bet-

ter relation to risk-return. With respect to the betas,

which represent the portfolio’s sensitivity in tracking

the market premium risk, the ﬁndings were not par-

ticularly signiﬁcant, with stand out to the prospect

model. It is important to note that, according to

(Ramos et al., 2023), betas below 1 indicate periods

of market downturn, which suggests that the results

highlighted in green reﬂect a lower sensitivity of the

portfolios in following this trend.

Table 5 presents very similar returns between the

two models, with a marginally notable performance

by the CVaR 99% model in terms of accumulated re-

turn. Regarding the risk metrics σ and SD(−), the

CVaR models stood out, except for the CVaR 99%,

which exhibited higher risk values. As for the metric

VaR, the prospect model was prominent, repeating the

relation observed in the previous table. Concerning

the risk-return reward measures, the CVaR model out-

performed across all three indices—Sharpe, Sortino,

and Starr. For the betas, the prospect model stood out

in both the benchmark and the bull market, whereas

the CVaR model excelled in the bear market.

The Table 6 revealed a different relationship for

the models in some performance metrics compared

to the previous tables. The results for accumulated

return, standard deviation, and the Sharpe ratio were

superior for the prospect model. However, for the re-

maining metrics in the table, including the betas at the

end of the columns, the CVaR model achieved supe-

rior results.

Additionally to the main case herein, an appli-

cation was held to the American market and an im-

portant sector, which is the Technology, was selected

to test the model under different market conditions.

Such results are exhibited in Table 7 that showed su-

perior results for the prospect model.

Notably, the prospect model achieved better re-

sults in Table 7 in terms of returns, all risk-return re-

ward metrics and in betas. On the other hand, it may

be considered more volatile considering the results of

(−)

and VaR’s. It’s also important to notice that

despite CVaR has been superior in a few metrics, It

lost its superiority in the risk-return reward metrics,

result that was observed in last three Tables regard-

Portfolio Optimization Based on Prospect Theory

Table 4: Performance Metrics for Electricity Sector.

Electricity Sector with 10 assets

Risk Cum. Ret. Avrg. Ret σ Sd(-) VaR Sharpe Sortino STARR β β

(+)

(−)

CVaR 90% 0.660043 0.000296 0.004005 0.003093 0.005198 0.074487 0.096447 0.021228 0.063460 0.021962 0.034169

CVaR 95% 0.721675 0.000323 0.003750 0.002445 0.005553 0.086910 0.133334 0.024408 0.058796 0.031897 0.017675

CVaR 99% 0.716388 0.000321 0.004031 0.002544 0.006466 0.080274 0.127206 0.023626 0.063441 0.034894 0.029544

Prospect 1.1 0.674502 0.000302 0.005146 0.004577 0.004899 0.059230 0.066595 0.019269 0.044670 0.013594 0.009173

Prospect 1.2 0.675335 0.000302 0.005186 0.004619 0.004904 0.058848 0.066068 0.019247 0.044737 0.014486 0.010847

Prospect 1.3 0.670603 0.000300 0.005161 0.004593 0.004855 0.058719 0.065979 0.019129 0.044491 0.013958 0.008974

Prospect 2.1 0.679653 0.000304 0.005282 0.004714 0.004759 0.058144 0.065154 0.019197 0.044561 0.009642 0.009642

Prospect 2.2 0.675522 0.000303 0.005286 0.004713 0.004878 0.057745 0.064772 0.019102 0.044797 0.012970 0.010225

Prospect 2.3 0.671259 0.000301 0.005193 0.004618 0.004844 0.058412 0.065689 0.019117 0.044337 0.013861 0.009103

Prospect 3.1 0.675058 0.000302 0.005234 0.004673 0.004826 0.058287 0.065288 0.019173 0.044373 0.013902 0.009264

Prospect 3.2 0.675102 0.000302 0.005254 0.004685 0.004814 0.058065 0.065116 0.019164 0.044457 0.013718 0.009633

Prospect 3.3 0.671439 0.000301 0.005202 0.004628 0.004840 0.058337 0.065574 0.019119 0.044684 0.014160 0.011265

Average 0.680548 0.000305 0.004894 0.004158 0.005070 0.063955 0.078935 0.020148 0.048900 0.017420 0.014126

Minimum

0.660043 0.000296 0.003750 0.002445 0.004759 0.057745 0.064772 0.019102 0.044337 0.009642 0.008974

Maximum 0.721675 0.000323 0.005286 0.004714 0.006466 0.086910 0.133334 0.024408 0.063460 0.034894 0.034169

Table 5: Performance Metrics for Banking / Financial Sector.

Banking / Financial Sector with 10 assets

Risk Cum. Ret. Avrg. Ret σ Sd(-) VaR Sharpe Sortino STARR β β

(+)

(−)

CVaR 90% 0.6749598 0.0003023 0.0044868 0.0032494 0.0064019 0.0679822 0.0938703 0.0200801 0.123820 0.101417 0.081619

CVaR 95% 0.6759288 0.0003027 0.0045429 0.0032063 0.0065380 0.0672376 0.0952662 0.0200886 0.131423 0.106065 0.085652

CVaR 99% 0.6923757 0.0003101 0.0048577 0.0033469 0.0073117 0.0643964 0.0934663 0.0202511 0.136302 0.131051 0.131051

Prospect 1.1 0.6749052 0.0003022 0.0045383 0.0036612 0.0063434 0.0672044 0.0833051 0.0192861 0.120924 0.083417 0.122114

Prospect 1.2 0.6749052 0.0003022 0.0045408 0.0036617 0.0063840 0.0671671 0.0832939 0.0192926 0.121436 0.091364 0.109767

Prospect 1.3 0.6749052 0.0003022 0.0045401 0.0036680 0.0063258 0.0671783 0.0831497 0.0192946 0.120832 0.083619 0.122911

Prospect 2.1 0.6749052 0.0003022 0.0045358 0.0036593 0.0063818 0.0672409 0.0833469 0.0193093 0.122353 0.084633 0.096643

Prospect 2.2 0.6749052 0.0003022 0.0045357 0.0036539 0.0063761 0.0672424 0.0834720 0.0193022 0.122592 0.091526 0.098825

Prospect 2.3 0.6749052 0.0003022 0.0045382 0.0036652 0.0063537 0.0672064 0.0832134 0.0193072 0.121781 0.085380 0.096273

Prospect 3.1 0.6749052 0.0003022 0.0045415 0.0036686 0.0063279 0.0671571 0.0831374 0.0192895 0.120903 0.083235 0.095485

Prospect 3.2 0.6749052 0.0003022 0.0045403 0.0036658 0.0063827 0.0671743 0.0831990 0.0192909 0.120822 0.084256 0.095347

Prospect 3.3 0.6749052 0.0003022 0.0045411 0.0036734 0.0063378 0.0671634 0.0830276 0.0193008 0.122256 0.090480 0.087357

Average 0.676451 0.000303 0.004562 0.003565 0.006455 0.067029 0.085979 0.019508 0.123787 0.093037 0.101920

Minimum 0.674905 0.000302 0.004487 0.003206 0.006326 0.064396 0.083028 0.019286 0.120822 0.083235 0.081619

Maximum 0.692376 0.000310 0.004858 0.003673 0.007312 0.067982 0.095266 0.020251 0.136302 0.131051 0.131051

Table 6: Performance Metrics for Oil & Gas Sector.

Oil & Gas Sector with 7 assets.

Risk Cum. Ret. Avrg. Ret σ Sd(-) VaR Sharpe Sortino STARR β β

(+)

(−)

CVaR 90% 0.6641466 0.0002974 0.0091415 0.0066263 0.0122230 0.0328367 0.0453010 0.0132606 0.308324 0.181852 0.466155

CVaR 95% 0.6573600 0.0002944 0.0091305 0.0065635 0.0122558 0.0325433 0.0452713 0.0131186 0.315649 0.190211 0.463402

CVaR 99% 0.6572365 0.0002943 0.0109428 0.0071091 0.0136906 0.0271487 0.0417893 0.0121112 0.317266 0.201762 0.458171

Prospect 1.1 0.6669770 0.0002987 0.0088806 0.0070480 0.0124028 0.0339440 0.0427702 0.0128963 0.339118 0.223844 0.579172

Prospect 1.2 0.6824364 0.0003056 0.0088822 0.0070543 0.0123860 0.0347175 0.0437133 0.0131909 0.338976 0.223784 0.576523

Prospect 1.3 0.6743679 0.0003020 0.0088779 0.0070511 0.0123787 0.0343271 0.0432208 0.0130430 0.339160 0.223198 0.577457

Prospect 2.1 0.6808568 0.0003049 0.0088809 0.0070452 0.0124080 0.0346429 0.0436695 0.0131690 0.338882 0.222711 0.575979

Prospect 2.2 0.6824364 0.0003056 0.0088829 0.0070409 0.0123409 0.0347145 0.0437968 0.0131996 0.338450 0.222083 0.577830

Prospect 2.3 0.6742435 0.0003019 0.0088805 0.0070465 0.0124059 0.0343110 0.0432409 0.0130474 0.339153 0.222908 0.577640

Prospect 3.1 0.6723612 0.0003011 0.0088903 0.0071144 0.0123583 0.0341783 0.0427098 0.0129719 0.340836 0.226336 0.577777

Prospect 3.2 0.6723612 0.0003011 0.0088808 0.0070555 0.0123709 0.0342150 0.0430663 0.0129987 0.338825 0.223488 0.574337

Prospect 3.3 0.6739684 0.0003018 0.0088798 0.0070591 0.0124090 0.0342997 0.0431463 0.0130376 0.339567 0.224591 0.578087

Average 0.671563 0.000301 0.009096 0.006984 0.012469 0.033490 0.043475 0.013004 0.332850 0.215564 0.548544

Minimum 0.657236 0.000294 0.008878 0.006563 0.012223 0.027149 0.041789 0.012111 0.308324 0.181852 0.458171

Maximum 0.682436 0.000306 0.010943 0.007114 0.013691 0.034717 0.045301 0.013261 0.340836 0.226336 0.579172

Table 7: Performance Metrics for Technology Sector - Nasdaq-USA.

Technology Sector with 10 assets.

Risk Cum. Ret. Avrg. Ret σ Sd(-) VaR Sharpe Sortino STARR β β

(+)

(−)

CVaR 90% 1.029705 0.000461 0.005352 0.003718 0.008104 0.060200 0.086651 0.002834 0.001390 -0.000772 0.001539

CVaR 95% 1.033281 0.000463 0.005450 0.003757 0.008420 0.059408 0.086177 0.002849 0.001055 -0.000936 0.000915

CVaR 99% 1.024239 0.000459 0.005610 0.003863 0.009021 0.056996 0.082763 0.002808 0.001798 -0.000760 0.001108

Prospect 1.1 1.062510 0.000476 0.005289 0.003889 0.008359 0.063689 0.086619 0.002960 0.001670 -0.000437 0.000803

Prospect 1.2 1.060851 0.000475 0.005290 0.003877 0.008400 0.063537 0.086693 0.002955 0.001644 -0.000470 0.001762

Prospect 1.3 1.060538 0.000475 0.005288 0.003882 0.008376 0.063530 0.086539 0.002953 0.001646 0.000705 0.000904

Prospect 2.1 1.062882 0.000476 0.005299 0.003898 0.008434 0.063605 0.086466 0.002962 0.001629 -0.000466 0.001744

Prospect 2.2 1.061604 0.000475 0.005291 0.003879 0.008406 0.063585 0.086745 0.002958 0.001609 -0.000499 0.001719

Prospect 2.3 1.063218 0.000476 0.005291 0.003883 0.008428 0.063728 0.086829 0.002964 0.001649 -0.000453 0.001760

Prospect 3.1 1.062743 0.000476 0.005298 0.003904 0.008413 0.063602 0.086323 0.002961 0.001692 -0.000417 0.000828

Prospect 3.2 1.063239 0.000476 0.005295 0.003891 0.008310 0.063676 0.086662 0.002964 0.001581 -0.000510 0.001698

Prospect 3.3 1.061254 0.000475 0.005288 0.003875 0.008442 0.063597 0.086779 0.002956 0.001652 -0.000455 0.001765

Average 1.053839 0.000472 0.005337 0.003860 0.008426 0.062429 0.086270 0.002927 0.001585 -0.000456 0.001379

Minimum 1.024239 0.000459 0.005288 0.003718 0.008104 0.056996 0.082763 0.002808 0.001055 -0.000936 0.000803

Maximum

1.063239 0.000476 0.005610 0.003904 0.009021 0.063728 0.086829 0.002964 0.001798 0.000705 0.001765

FEMIB 2025 - 7th International Conference on Finance, Economics, Management and IT Business

ing the Brazilian study. These ﬁndings suggest that

the prospect model has tendency to seek more gains

in proﬁtable markets, getting therefore a better perfor-

mance, but also under higher volatility. When the sce-

nario is characterized by losses it may be quite conser-

vative, changing this feature. This can be justiﬁed by

the fact that the stocks in Technology sector have de-

livered higher returns and have been quite proﬁtable

during the time horizon considered, or over almost 8

years. Differently from Brazilian sectors that had re-

turns nearly 30% less over the same time horizon.

In some of the results, it is possible to notice that

the prospect model exhibited a propriety of higher

volatility as observed in (Pﬁffelmann et al., 2016).

This feature can be observed through Table 4 and par-

tially in Table 5 and 7.

Finally, both models were considered suitable for

this application and the prospect model delivered re-

sults suitable and comparable to CVaR’s in many in-

stances. It’s possible to infer that in some occasions

discussed, prospect model delivered more volatility

and very similar results in all sectors, specially in the

ﬁnancial sector for Brazilian study (Table 5) and for

the American study in Table 7. On the other hand,

CVaR delivered a better relation of reward return-risk

in all Brazilian sectors.

Next section presents overall conclusions and sug-

gests opportunities to continue this study.

4 CONCLUSIONS

This paper has elucidated the signiﬁcant potential of

utilizing prospect theory in the context of portfolio

optimization. By the interpretation of the results from

the proposed prospect model, an alignment with the

outcomes of a traditional optimization model was ob-

served in many instances.

The primary advantage of integrating prospect

theory into portfolio optimization lies in its ability

to assign different weightings to gains and losses,

thereby accommodating speciﬁc needs of the decision

makers. This approach also enables the weighting

for losses in distinct segments, thus allowing simulate

different scenarios.

The results of this paper were analyzed using port-

folios composed of assets from three different sec-

tors for Brazilian case and one more sector within

the American case. This approach was crucial for

evaluating both models when selecting assets under

distinct conditions, thereby avoiding undesirable bi-

ases. The alignment of these results demonstrated the

consistency of the new model as an alternative tool

for decision-making analysis under uncertainty in the

context of investments. This was the primary goal of

this paper, that is, to provide an alternative mathemat-

ical model with a level of efﬁciency comparable to

well-established mathematical approaches in the spe-

cialized literature.

While the proposed model exhibited similarities

to CVaR’s in most of instances, it also demonstrated

inconsistencies in some of the results. These ﬁnd-

ings underscore the necessity for further reﬁnements.

Future researches should focus on calibrating all pa-

rameters, particularly the break-point of the func-

tion based on the idea of the kink). Besides future

researches could propose more break-points for the

functions testing different parameters for the betas.

This would increase the number of binary variables

and might provide opportunities of reﬁnements.

In conclusion, the application of prospect theory

to portfolio optimization problems holds promise, but

it also presents challenges that require attention and

ongoing reﬁnement to fully achieve its potential.

ACKNOWLEDGEMENTS

The ﬁrst author received ﬁnancial support from

CNPq (Brazilian National Research Council), grant

308909/2021-6.

REFERENCES

Artzner, P., Delbaen, F., Eber, J. M., and Heath, D. (1999).

Coherent measures of risk. Mathematical Finance,

9:203 – 228.

Asghari, M., Fathollahi-Fard, A. M., Mirzapour Al-e

hashem, S. M. J., and Dulebenets, M. A. (2022).

Transformation and linearization techniques in opti-

mization: A state-of-the-art survey. Mathematics,

10(2).

B3 (2025).

Indice bovespa (ibovespa b3). B3 - Brasil,

Bolsa, Balc

ao.

B3-IEE (2025).

Indice de energia el

etrica (iee b3). B3 -

Brasil, Bolsa, Balc

ao.

Barberis, N., Huang, M., and Santos, T. (2001). Prospect

Theory and Asset Prices*. The Quarterly Journal of

Economics, 116(1):1–53.

Barberis, N. and Thaler, R. (2003). Chapter 18 a survey

of behavioral ﬁnance. In Financial Markets and Asset

Pricing, volume 1 of Handbook of the Economics of

Finance, pages 1053–1128. Elsevier.

Benartzi, S. and Thaler, R. (1995). Myopic Loss Aversion

and the Equity Premium Puzzle*. The Quarterly Jour-

nal of Economics, 110(1):73–92.

Best, M., Grauer, R., Hlouskova, J., and Zhang, X. (2014).

Loss-aversion with kinked linear utility functions.

Computational Economics, 44(1):45–65.

Portfolio Optimization Based on Prospect Theory

Best, M. and Zhang, X. (2011). Degeneracy resolution for

bilinear utility functions. J. Optimization Theory and

Applications, 150:615–634.

Best, M. J. and Grauer, R. R. (2016). Prospect theory and

portfolio selection. Journal of Behavioral and Exper-

imental Finance, 11:13–17.

Best, M. J. and Grauer, R. R. (2017). Humans, econs

and portfolio choice. Quarterly Journal of Finance,

7(02):1750001.

De Giorgi, E., Hens, T., and Rieger, M. O. (2010). Finan-

cial market equilibria with cumulative prospect the-

ory. Journal of Mathematical Economics, 46(5):633–

651. Mathematical Economics: Special Issue in hon-

our of Andreu Mas-Colell, Part 1.

Group of Thirty (1993). Derivatives, Practices and Princi-

ples. Number 3 in Derivatives: practices and prin-

ciples - Global Derivatives Study Group. Group of

Thirty.

Jorion, P. (2006). Value at Risk, 3rd Ed.: The New Bench-

mark for Managing Financial Risk. McGraw Hill

LLC.

udice, J. J., Ribeiro, C. O., and Santos, J. (2003). An

alise

comparativa dos modelos de selecc¸

ao de carteiras de

ac¸

oes de markowitz e konno. Investigac¸

ao Opera-

cional, 23:211–224.

Kahneman, D. and Tversky, A. (1979). Prospect theory:

An analysis of decision under risk. Econometrica,

47(2):263–291.

Kahneman, D. and Tversky, A. (1992). Advances in

prospect theory: Cumulative representation of uncer-

tainty, pages 297–323. Springer.

Konno, H. and Yamazaki, H. (1991). Mean-absolute de-

viation portfolio optimization model and its applica-

tions to tokyo stock market. Management Science,

37(5):519–531.

Mainik, G., Mitov, G., and R

uschendorf, L. (2015). Portfo-

lio optimization for heavy-tailed assets: Extreme risk

index vs. markowitz. Journal of Empirical Finance,

32:115–134.

Markowitz, H. M. (1952). Portfolio selection. The Journal

of Finance, 7(1):77–91.

Pﬁffelmann, M., Roger, T., and Bourachnikova, O. (2016).

When behavioral portfolio theory meets markowitz

theory. Economic Modelling, 53:419–435.

Ramos, H. P., Righi, M. B., Guedes, P. C., and M

uller, F. M.

(2023). A comparison of risk measures for portfolio

optimization with cardinality constraints. Expert Sys-

tems with Applications, 228:120412.

Rockafellar, R. and Uryasev, S. (2002). Conditional value-

at-risk for general loss distributions. Journal of Bank-

ing & Finance, 26(7):1443–1471.

Rockafellar, R. T. and Uryasev, S. (2000). Optimization of

conditional value-at risk. Journal of Risk, 3:21–41.

Sortino, F. and Satchell, S. (2001). Managing Down-

side Risk in Financial Markets: Theory, Practice,

and Implementation. Quantitative ﬁnance series.

Butterworth-Heinemann.

Wang, J., Wu, C., and Zhong, X. (2021). Prospect theory

and stock returns: Evidence from foreign share mar-

kets. Paciﬁc-Basin Finance Journal, 69:101644.

Zhong, Y., Li, Y., Yang, Y., Li, T., and Jia, Y. (2022). An

improved three-way decision model based on prospect

theory. International Journal of Approximate Reason-

ing, 142:109–129.

FEMIB 2025 - 7th International Conference on Finance, Economics, Management and IT Business