Reconstruction of the Botanical Trees from Single-View Images Using
Signed Distance Functions
Anna Semrau
a
and Dariusz Sawicki
b
Warsaw University of Technology, Warsaw, Poland
Keywords: Botanical Trees Modeling, Fractals, Single-View Image Reconstruction, Signed Distance Functions,
Bounding Volumes, Procedural Generation.
Abstract: Fractal modeling methods revolutionized the approach to modeling objects in computer graphics. They made
it possible to create natural objects, where mathematical description using traditional Euclidean Geometry is
difficult or even impossible. Plants, especially trees, are a perfect example of this type of objects. However,
fractals, due to their properties, create application problems, related to the generation process. One of the new
attempts to solve these problems is modeling 3D objects from single-view images. Signed distance functions
(SDF), when combined with ray marching, represent a traditional yet underutilized technique that
demonstrates significant potential for fractal modeling. The aim of the article is to analyze the possibility
of using this method to increase the efficiency of tree modeling, focusing on the 3D reconstruction. We have
proposed a novel method for reconstructing the 3D geometry of botanical trees from single-view photographs,
which is based on the SDF.
1 INTRODUCTION
1.1 Motivation
Modern graphic rendering engines such as Unreal
Engine (Unreal Engine, 2024) or Unity (Unity, 2024)
allow users to create realistic worlds to fulfill growing
expectations of the computer games industry and
cinematography. When watching a film or playing
a game, the recipient wants to feel engaged in the
created world. Graphic tools should provide him with
the opportunity to achieve a strong sense of
immersion in virtual reality (VR) (Berkman and
Akan, 2019). Some of the most important image
elements for VR are trees, plants and terrain (Deussen
and Lintermann, 2005, Xiao et al., 2024). Despite the
rapid development of computer hardware and graphic
algorithms in recent years, creating a complex image
for the needs of virtual reality is still a huge challenge
for programmers and hardware designers.
The idea of "fractal" (also the term itself) and the
principles of fractal modeling were proposed in the
1970s by B. Mandelbrot (Mandelbrot, 1983).
Currently, fractal modeling methods are used in
a
https://orcid.org/0009-0001-0410-3248
b
https://orcid.org/0000-0003-3990-0121
various fields: physics, biology, economics, and even
art (Barnsley, 2012, Peitgen et al., 2013, XenoDream
Software, 2024). However, in computer graphics,
Mandelbrot's idea revolutionized the approach to
modeling objects. It made it possible to create natural
objects or other components of the real world, where
mathematical description using traditional Euclidean
Geometry is difficult or even impossible. Already in
the introduction to his book "The Fractal Geometry of
Nature" (Mandelbrot, 1983), the author points out the
difficulties of describing the irregularities of the
natural (real) world and proposes fractal geometry,
which effectively solves this problem.
Mandelbrot's revolutionary idea allows for
an excellent description of the "natural world", but
the implementation and technical problem remains.
Even for modern computers, creating a world of
plants for the needs of virtual reality (VR), games, or
film animations is still a difficult task. We still have
to accept a certain compromise between the level of
detail of the modeled fractal shapes and the efficiency
and control over the computational process. This
problem particularly stands out in the foliage
modeling, especially when it comes to species fidelity
376
Semrau, A. and Sawicki, D.
Reconstruction of the Botanical Trees from Single-View Images Using Signed Distance Functions.
DOI: 10.5220/0013335300003912
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 376-384
ISBN: 978-989-758-728-3; ISSN: 2184-4321
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

and detailed shaping. For cases with a required lower
level of detail, the problem may seem exaggerated.
After all, if we create a virtual world and draw
a landscape, the vegetation serves mostly as
a background, like a forest or a field.
In some cases, plants have to be depicted in much
more detail, hand-crafting which would be time-
consuming. Despite the fractal patterns observed in
naturally occurring objects, they are shaped
irregularly and non-repeatably, so they must be
modeled as such to look realistic. To address the
constantly growing demand, the need arises, for
creating a generation pipeline that can provide any
level of detail, while being fast and efficient.
An additional aspect to consider is the potential
automation of the process, which is important for
recreating captured real-data input. This is
increasingly being utilized with the growing
popularity of AI and advancements in computer
vision techniques.
Those considerations led to the proposal of
modeling trees (and possibly other natural objects)
using shape reconstruction based on a single-view
image of the object. Model reconstruction from
a single image is a new tendency (Li et al., 2021). In
our opinion, it is one of the most interesting areas of
research of fractal modeling proposed today in
computer graphics. Our article addresses the
challenge of creating data from images without
requiring a complex dataset of images, 3D models,
and semantic masks for building a machine learning
generative pipeline. In contrast to other objects
studied for geometry reconstruction, trees and plants
are difficult to scan due to their complexity, and to the
best of our knowledge, there is no such dataset
available to the public.
1.2 The Aim of the Article
Modern VR creation systems and professional
graphic applications with realistic (hyperrealistic
even) presentation quality depend heavily on various
ray tracing (RT) techniques. On the other hand, RT is
a method that allows the use of very different
algorithms, as long as they give effective results. One
such algorithm is ray marching, which was forgotten,
and has been "reborn" in recent years. Ray marching
operates with the object description using signed
distance functions (SDF). Research from recent years
(Semrau and Sawicki, 2024) confirms the great
usefulness of this algorithm in fractal modeling using
RT techniques.
The aim of this article is to analyze the
possibilities of effective use of signed distance
functions to generate 3D plant fractals. We create
an approximated bounding volume described by the
SDF from the binary mask of the tree silhouette and
use it to limit the plant growth generated from the
parametric system.
2 RAY MARCHING WITH SDF IN
PLANTS MODELING AND 3D
FRACTAL RECONSTRUCTION
– THE STATE OF THE ART
The fractal technique is currently considered the best
way to model plants or other natural objects. On the
other hand, visualizing 3D fractals is a complex
process.
Ray marching and signed distance functions
(SDF) were first used as techniques to support ray
tracing in the modeling and visualization of fractals
in the 1980s (Tuy and Tuy, 1984, Perlin and Hoffert,
1989, Hart et al., 1989). For many years, SDFs were
rarely used. In recent years, they have reappeared as
techniques for "special tasks" such as shading
determination or ambient occlusion using SDF (Mesh
Distance Fields, 2023). We can also find many
websites dedicated to ray marching (Wong, 2016,
Bovenzi, 2022, Walczyk, 2023). In particular, tools
incorporate distance mesh components: Unreal
Engine (Mesh Distance Fields, 2023) and Unity
(Raymarching, 2020).
Today, numerous articles showcase fascinating
examples of using ray marching and SDF to create
fractals (Angramme, 2021; Petrov, 2020). However,
in our view there are few, published studies on
applying ray marching and SDF for fractal modeling
of plants. To the best of our knowledge, there are also
no reports on utilizing these techniques for
reconstructing 3D fractals from single-view images.
The problem of 3D reconstruction of an object
based on its images has been known in computer
graphics for many years. However, it has always been
done using multiple views rather than a single-view
image. There are known proposals for reconstruction
based on a set of images including different views
(Reche-Martinez et al., 2004, Neubert et al., 2007), or
simply a sequence of subsequent images related to
movement (Quan et al., 2006). One of the first
attempt to reconstruct a plant as a 3D object based on
a single-view image was the method proposed by
(Tan et al., 2008). The authors reconstructed the tree's
shape using a pre-existing template, aligning the
single-view image with the corresponding branch
structure. However, this method required user
Reconstruction of the Botanical Trees from Single-View Images Using Signed Distance Functions
377

intervention to manually identify the main branches.
In our opinion, the most interesting proposal for using
single-view images for 3D tree reconstruction is
presented in the work (Li et al., 2021). Their method
eliminates the need for manual input and generates
a plausible tree shape that aligns not only with the
tree's species but also with its single-view image.
3 MATERIALS AND METHODS
3.1 3D Fractal Modeling – Main
Assumptions
The vast complexity and diversity of natural objects
make it impossible to develop a universal fractal
description (Peitgen et al., 2013; Barnsley, 2012).
Among the most widely used approaches are rule-
based methods such as the Iterated Function System
(IFS) and the Lindenmayer system (L-system).
IFS is a method of generating fractals, defined as
a set of affine transformations. The application of IFS
is the result of the work of John Hutchinson and
Michael Barnsley (Barnsley, 2012).
In computer graphics, fractal modeling allows
primarily the creation of realistic shapes of natural
objects. A typical example is fractal plants: trees or
flowers. In this case, the most important feature of
fractals is self-similarity, i.e. the entire object has a
similar shape as one or more of its parts. This property
is frequently observed in nature, particularly in plants,
where the branching structure of trees and the shapes
of leaves exhibit self-similarity. Based on this, in
1968 Astrid Lindenmayer proposed L-systems to
describe them (Prusinkiewicz and Lindenmayer,
1990). L-system corresponds to the context-free
grammar in the Chomsky hierarchy. L-systems define
an object in a recursive way, using an axiom (initial
state) and a set of production rules describing the
steps that must be applied in each iteration. Of course,
the L-system is not the same as Chomsky's grammar.
The fundamental difference between these
approaches is that L-systems productions are used in
parallel (e.g. simultaneously replacing all letters in
a given word) and not sequentially (Prusinkiewicz
and Lindenmayer, 1990).
In our approach to fractal modeling, we used
a parametric growth model, derived from basic L-
system operations. We used part of the standard
botanical parameters (Stava et al., 2014) to grow
branches accordingly. In contrast to the standard L-
system, this method allows for checking each node
against the bounding conditions at any given moment
and marking it as stale. It is possible to use shaping
for models already produced with L-systems, but then
the problem of them not having a sufficient amount
of branches might occur. We decided to use
transformational operations known from L-systems
such as rotation, yaw, pitch, and growing a new shoot,
and combine them with parameters controlling the
amount of branching, length of internodes, and
direction of growth.
The following set of initial assumptions was made
to build the software.
 An approximate bounding volume can be
reconstructed using a binary mask representing
the tree's silhouette.
 An SDF can describe this bounding volume by
utilizing cylinders and operations.
 The reconstruction is performed procedurally,
requiring no prior input data apart from the
species-specific parameters for the growth
system.
 The model mesh construction and rendering will
be done in Unreal Engine, using the provided
components for splines and basic mesh shapes.
 Splines (spline meshes) represent the tree
branches and can be deformed in the same
manner as in L-system transformations.
 Users can add texturing, and further adjust the
shape of the generated model.
 Generated trees can be converted to static meshes
that can be used in real-time applications.
3.2 Signed Distance Functions (SDF)
and Their Visualization
SDF calculates the distance (typically Euclidean)
from a given point to the surface of an object, with the
sign indicating whether the point is inside or outside
the object's boundary. This makes SDF an effective
tool for defining bounding volumes for objects. It can
also be used to determine a level of detail (LOD) by
calculating the distance between the viewer and the
object it represents.
In this method, data is embedded directly into the
code using mathematical functions, requiring it to be
described through one of several model definitions.
Distance function formulas for basic 3D shapes are
relatively simple to define, making them ideal for
input into SDF-based constructive solid geometry
(CSG) operations such as intersection, union, and
subtraction (Requicha and Voelcker 1977, Foley et
al., 1996). The process of building the CSG tree
mirrors that of standard 3D models represented by
meshes. Furthermore, blending objects constructed
from CSG primitives can be quite simple, using
polynomial smoothing functions (Quilez, 2013).
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
378

Figure 1: Illustration of ray marching algorithm. Green
circles (spheres): distance estimations (SDF), the centers of
the spheres (green dots) indicate the next marching steps
along the ray (from left to right). Figure based on (Semrau
and Sawicki, 2024).
Rendering SDF typically utilizes a technique
called ray marching, also known as sphere tracing
(Hart, 1996). This method, a variant of path tracing,
determines where a ray intersects an object in a scene
by iteratively estimating distances.
A ray is represented by a pair, consisting of:
a point in space representing a current position, and
a direction vector. Distance estimation in ray
marching is an iterative process. The virtual camera’s
position sets the initial point for the first iteration. In
each iteration, the distance represents the maximum
distance the ray can travel in its direction without
hitting an object. The ray advances by this distance,
"marching" (Figure 1) forward until distance is
smaller than a pre-set threshold.
3.3 Botanical Tree (3D Object)
Reconstruction from Single-View
Image
Reconstructing a 3D object based on its single-view
image is a difficult task. From a formal perspective,
reconstructing a full 3D object from a single-view
image is fundamentally unsolvable, as a single image
lacks sufficient information to define the entire
object. However, when it comes to trees (or other
plants), we can observe that plants of the same species
share a high degree of similarity, which can be
leveraged to approximate their 3D structure. This is
even more than fractal self-similarity because it also
occurs between different objects. Additionally, we
usually treat plants in a virtual landscape as
a background and we are not that interested in the
detail of their three-dimensional shape. A single-view
image allows us to determine one cross-section of
a 3D object. We can assume that a tree is, in a sense,
a rotationally symmetric object. However, there are
disturbances to this symmetry resulting from the
species, tropisms (e.g. geotropism), or other factors
that can be considered random. In this case, adding
a disturbance to rotational symmetry will allow us to
reconstruct a 3D object (such as a tree) based on
a single-view image. This type of solution was
proposed in the paper (Li et al., 2021).
In our approach, we used SDF to construct
a bounding volume from a binary mask. The same
approach can be used for any object mask, provided
that the shape is continuous (Figure 2). Using CSG
boolean operations, we combine basic primitives to
form the approximate shape of the 3D model mapped
as a signed distance function. Using the created
function we evaluate the distance of the growing
branch’s apical bud from the bounding surface. Using
SDF-based check is a convenient method to interrupt
the growth, as the function returns positive values
only when the point lies outside of the volume.
3.4 Reconstruction from Mask
Parametric systems offer a degree of flexibility and
realism but can be challenging to control when
precise shape definition is required. To address these
challenges, researchers have developed various
approaches that utilize input data to reconstruct a
tree's shape.
Figure 2: The idea of our reconstruction method: from a single-view image of the real tree (left) to the reconstructed, fractal
modeled artificial tree. The bounding volume is constructed from binary mask using SDF. The SDF is mapped using primitive
shapes (red and green figures).
Reconstruction of the Botanical Trees from Single-View Images Using Signed Distance Functions
379

Input data can include images (single- or multi-
view) or point cloud data. Images require additional
processing before reconstruction, as multiple
potential 3D shapes can correspond to a single 2D
projection. Existing methods often rely on multiple
images and point clouds (Tan et al., 2007) or require
user-defined alterations (Tan et al., 2008).
More recently, these challenges have been tackled
using machine learning techniques. A common task
involves detecting a tree's outline in an image through
semantic segmentation, followed by reconstructing
a bounding volume from this outline. Both tasks
require large datasets, which, to the best of our
knowledge, must either be synthesized (Li et al.,
2021) or created by combining real-life images with
3D models reconstructed from point cloud data.
However, collecting point cloud data alongside
images is a time-consuming and complex process.
Studies have shown that networks trained on
synthesized datasets perform well on real-world
examples (Li et al., 2021). Creating such datasets
involves building a comprehensive framework that
includes functional parametric systems to generate
models, images, and corresponding binary masks.
In contrast, we propose a reconstruction method
that assumes the binary mask has already been
obtained. Our approach requires only the mask of the
tree's silhouette, which can be a manually created
sketch or a semantic mask generated by a neural
network. This method can be applied to any
reconstruction system, either during the model
creation process or to modify an existing model. For
this paper, we chose to use the simplified version of
Stava's parametric system (Stava et al., 2014).
4 REALISATION
4.1 SDF Reconstruction from Binary
Mask – the Algorithm
Our method allows for constructing a spatially-
bounded three-dimensional tree model, based on the
binary mask representing the silhouette of the tree.
The mask is being processed to find the root, main
apical axis, and tree crown, which are converted to
SDF representation. There are many methods to
represent the bounding volume for a tree. Inspired by
radial bounding volumes (RBV) (Li et al., 2021), our
method maps the SDF using cylinders for tree
segments (Figure 3). However, using SDF gives the
possibility of improved implementation efficiency
both in terms of memory usage and execution speed
(Semrau and Sawicki, 2024).
Figure 3: Mapping examples: The binary mask represents
the tree's silhouette, the SDF is mapped using primitive
shapes (red and green figures), and cylinders are applied to
the corresponding tree segments (bottom row).
Our method consists of four main stages to
construct an SDF mapping of the approximated
bounding volume for the tree.
The first stage is to morphologically process the
mask and smooth the edges with median blur to avoid
discontinuities. The details do not contribute
significantly to the overall shape, but they could
distort the radius calculation, especially for the root
detection.
The second stage is to locate the root and the
main vertical axis of the tree (using sliding window
and further distribution smoothing, we calculated the
location of the root alongside the major axis).
The third stage. Based on that information, we
place the marker alongside the axis at the top of the
root.
The fourth stage is to iteratively search for the
cylinder radius on each side of the axis. The image
scale must be normalized for this method to function
correctly. Instead of cylinders, SDF primitives such
as cubes or spheres can be used (Figure 4).
We experimented with the step size, setting it to
either an even value or the height of the smaller
radius. A smaller step size allows for a more accurate
approximation, as indicated by the similarity metrics
comparing the obtained model to the original mask.
With the obtained parameters a mapping function
calculates a SDF for each point along the vertical
axis. The mapping function iteratively computes the
distance from the point to each cylinder. These
distances are combined using a union operation. The
function adjusts the input position and iterates over
the list of cylinders to refine the distance values,
ultimately returning the signed distance to the entire
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
380

shape formed by the cylinders. To separate the left
and right sides, the cylinders were sliced with the
vertical plane and blended initially on each side.
Afterward, both sides were interpolated (Figure 4).
This function takes a 3D coordinate as an input and
returns the distance to the tree bounding volume, so it
is used for each node to check if the shoot should be
marked as stale or remain active for the next cycle of
growth.
Figure 4: SDF mappings comparison. Sphere as a primitive
on the left, cylinders in the middle, smooth interpolation
example on the right.
4.2 Rendering of the Detailed Models
The algorithm for calculating the primitive's
coordinates was implemented using OpenCV. The
growth model and mapping function were written in
C++ in Unreal Engine version 5.4. To visualize the
SDF volume the mapping function was also written
in OpenGL Shading Language (GLSL, 2021) and
visualized using Shadertoy (Shadertoy, 2013). The
research was carried out using the graphics card
NVIDIA® GeForce® RTX 4060 GPU.
During each growth cycle, the algorithm evaluates
each branch and its nodes to determine if they are
eligible to grow new branches. Buds are either
spawned or pruned based on age and a probabilistic
decay factor. The function also includes a "branch
death" mechanism, where branches have a chance of
becoming inactive. New nodes are added to the
branches according to the growth rate, and the
coordinates for the tree's geometry are recalculated.
Each node's validity is checked against the tree's
shape and height, with adjustments made to maintain
a realistic structure. Finally, new branches are
incorporated, and the updated tree structure is
returned. The algorithm incorporates probabilistic
elements for growth, bud survival, and branch death,
resulting in a dynamic, evolving tree model.
Branches represented as point lists are merged if
they share connecting points. These merged branches
are then used to create spline objects, which are
assigned static meshes for further representation.
5 RESULTS AND DISCUSSION
5.1 Obtained Results
The tests were performed on a set of botanical trees
photos (single-view images) from the collection from
Kaggle (Random Trees, 2023). Trees of different
species, with different sizes, different leaf coverage
and different perceived shapes were selected for
testing (Figure 5). The perceived shape is
immediately visible in the silhouette (and mask) of
a given tree. Examples of photos that do not contain
the entire tree were also included – the photographer
captured a selected fragment of the tree.
Ideally, images should depict complete
silhouettes, but our method can produce results with
incomplete masks as well smooth interpolation used
in reconstruction can help reduce sharp edges, but the
SDF approximation cannot fully compensate for
missing information about the rest of the shape.
Occluded or incomplete areas may be challenging to
convert into masks, but using SDF interpolation can
assist in creating objects that appear realistic from all
directions.
Figure 5: Single-view image and appropriate binary mask of reconstructed trees.
Reconstruction of the Botanical Trees from Single-View Images Using Signed Distance Functions
381

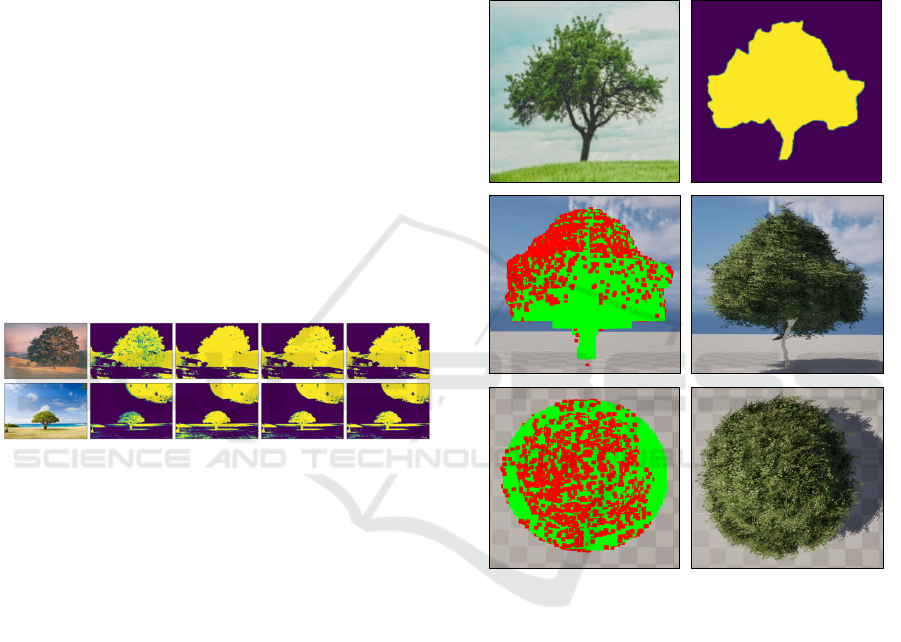
5.2 Binary Mask Quality
The factor that determines the quality of the entire
tree building process is the quality of the mask. In
addition, this problem is not strictly related to the
proposed algorithm. It depends largely on the quality
of the single-view photo.
We tested various examples of masks with
different algorithms for calculating the main axis of
the silhouette and automatic detection of the tree on
the image. One of the main issues remaining is that if
the tree has a similar color to the background, then it
could not be properly converted to a mask without
using a dedicated neural network or manual selection
(Figure 6). Other issue is finding the main vertical
axis if the root is tilted. We tested various methods for
shape or detected root, Principal Component Analysis
(PCA), major axis length and every time a root
centroid detection worked best, combined with
vertical axis. It is also highly preferable to have
a complete silhouette withing the processed image.
We could increase the SDF interpolation to mitigate
the effect of not having a complete outline of the
shape, so the model would remain realistic.
Figure 6: Imprecise mask detection. Problems occur if the
background is similar to the tree color, like grass, forest, etc.
5.3 Obtained Results – Stages of the
Reconstruction
Figure 7 depicts a photograph of the object in its
natural environment, the mask created from the
original photograph, highlighting the object's key
features. Tree model is being generated from the
mask – a three-dimensional visualization based on
contours derived from the initial image. Foliage is
added by the generator as mesh planes alongside the
branches and at their ends. Figure depicts different
perspectives of the same tree model.
5.4 Discussion
The implementation successfully reconstructs realistic
3D models of botanical trees from single-view
photographs, starting with only a binary mask of the
tree’s silhouette. Our method integrates mechanisms
like growth cycles and node evaluation to refine the
tree structure dynamically, ensuring realistic results.
One of the most important advantages of the
proposed solution is the complete separation of
functions in the process of creating a tree. On the one
hand, fractal modeling and the "growth" of the tree
and its branches, on the other hand, the final
rendering. Both tasks are completely independent and
well-controlled. Thus, we can choose the leaf cover
for the same tree, e.g. for the appropriate season: lush,
fresh green, small spring leaves, or a few large and
yellowed autumn leaves (Figure 8).
Figure 7: Examples of final trees – reconstruction stages.
Red points represent branches intersections with the SDF
surface, marked in green. Foliage hides the discontinuities
between cylinders.
There is another feature of shape modeling worth
nothing in our algorithm and SDF. The target tree
(final rendering result) may have a slightly different
shape than that suggested by the single-view image –
apart from the fact that the single-view image does
not provide full information about the shape of the
entire tree. In the branch growth we used a random
factor, and so trees of the same species will never be
identical – which, in fact, is completely natural. The
issue is similar with the leaf coverage – the random
factor affects a given, specific case of the tree. Of
course, the shape of the obtained tree is
"subordinated" to the SDF constraints, but each tree
will grow individually and in its own way. This
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
382

approach is, in our opinion, most consistent with the
changes in the shape of real botanical trees.
Figure 8: Examples of leaf cover for different seasons.
One issue that always occurs in exponentially
complex problems is memory management and
performance. We opted for dynamic memory
allocation for splines that had sufficient amount of
nodes, to prevent performance degradation or
excessive memory usage. Our mesh models took 10s
on average to generate, up to 1 minute for texture
application (depending on an amount of splines) and
can be then rendered in real time. Another challenge
involved dynamically controlling the growth process
using SDF limitations. Additionally, scaling the SDF
to match the expected size of the tree proved critical.
Incorrect scaling could result in the tree's shape being
either underfilled or overfilled, compromising the
accuracy and realism of the reconstruction.
The use of SDF gives us the opportunity to work
with incomplete masks. Of course, in such a situation
we will not recreate the missing information, but
interpolation allows for a realistic appearance from all
directions. On the other hand, one could consider
using AI to recreate the missing fragments, knowing
what species we are dealing with. However, this is
such a complex issue that it requires completely
independent research.
5.5 Further Improvements
The algorithm for mapping SDF from binary mask
could be further improved to be prone to edge cases.
An additional advantage would be to use a semantic
segmentation system to obtain masks automatically
and identify main branches to preserve even more
accuracy. This would also allow our method to be
scalable on the large sets of images. Additionally, we
should implement a method to detect the main visible
branches, ensuring that prominent branches are
copied from the input image, rather than just the
silhouette. The function can also be used to change
the coordinates to lean toward the bounding sphere.
In addition to refining growth parameters, the
simplified parametric generation system could be
further improved by adding tropisms. Optimizing
spline allocation, such as reducing the number of
internodes and merging splines, could significantly
improve performance by decreasing computational
overhead. Furthermore, leveraging SDF
representations for other objects in the environment
could prevent collisions during the growth process.
This approach is particularly promising for
simulating ecosystems, where interactions between
multiple objects must be considered, and could also
be applied to animations to create dynamic, lifelike
scenes.
6 SUMMARY
3D object reconstruction from a single-view image
has emerged as one of the most intriguing methods
for fractal modeling in recent years. We propose
a novel approach for reconstructing the 3D geometry
of botanical trees from single-view photographs,
utilizing signed distance functions (SDF). This
method, combined with ray marching, has proven to
be highly effective in fractal modeling.
Our article demonstrates how SDF can address the
challenge of insufficient 3D data for object
reconstruction. By transforming a binary mask of
a tree silhouette into a 3D model, the resulting object
can be saved, imported into any tool, textured, and lit
like a regular scene object. SDF offers an intuitive yet
efficient solution to this problem and is
straightforward to implement, with flexibility for
adjustments to suit various needs.
The reconstruction stages were visualized using
OpenCV, Unreal Engine, and ray marching rendering
in Shadertoy. We believe this mapping function is
highly versatile and can seamlessly integrate with
various generation systems. Moreover, this approach
could mitigate a significant obstacle in Machine
Learning-enhanced methods: the need for highly
specific datasets.
REFERENCES
Angramme (2021). Fractal_viewer. https://github.com/
Angramme/fractal_viewer. (Accessed 10 November
2024).
Barnsley, F.B. (2012). Fractals Everywhere: New Edition.
Dover Publications Inc.; 3rd revised edition.
Berkman, M.I., Akan, E. (2019). Presence and Immersion
in Virtual Reality. In: Lee, N. (eds) Encyclopedia of
Computer Graphics and Games. Springer, Cham.
https://doi.org/10.1007/978-3-319-08234-9_162-1.
Bovenzi, T. (2022). Ray Marching. https://www.tylerboven
zi.com/RayMarch/ (Accessed 10 November 2024).
Reconstruction of the Botanical Trees from Single-View Images Using Signed Distance Functions
383

Deussen, O., Lintermann, B. (2005). Digital Design of
Nature. Computer Generated Plants and Organics.
Springer-Verlag Berlin Heidelberg.
Foley, J.D., van Dam, A., Feiner, S.K., Hughes J.F. (1996).
Computer Graphics: Principles and Practice, sec. ed.
Addison-Wesley.
GLSL. OpenGL Shading Language. (2021). OpenGL Wiki.
http://www.khronos.org/opengl/wiki_opengl/index.ph
p?title=OpenGL_Shading_Language&oldid=14750.
(Accessed 11 January 2025).
Hart, J.C., Sandin, D.J., Kauffman, L.H. (1989). Ray
Tracing Deterministic 3-D Fractals. ACM SIGGRAPH
Computer Graphics. 23 (3), July 1989. 289–296.
https://doi.org/10.1145/74334.74363.
Hart, J.C. (1996). Sphere tracing: a geometric method for
the antialiased ray tracing of implicit surfaces. The
Visual Computer 12, December 1996. 527-545.
https://doi.org/10.1007/s003710050084.
Li, B., Kałużny, J., Klein, J., Michels, D.L., Pałubicki, W.,
Benes, B., Pirk, S. (2021). Learning to reconstruct
botanical trees from single images. ACM Trans. Graph.
(TOG), 40 (6), Dec. 2021, Article No. 231, 1-15.
https://doi.org/10.1145/3478513.3480525.
Mandelbrot, B.B. (1983). The fractal geometry of nature.
W.H.Freeman & Co Ltd.
Mesh Distance Fields. (2023). Mesh Distance Fields.
https://docs.unrealengine.com/4.27/en-
US/BuildingWorlds/LightingAndShadows/MeshDista
nceFields/. (Accessed 11 November 2024).
Neubert, B., Franken, T., Deussen, O. (2007). Approximate
Image-based Tree-modeling Using Particle Flows.
ACM Trans. Graph. (TOG). 26 (3), 88–es.
https://doi.org/10.1145/1276377.1276487.
Peitgen, H-O., Hartmut, J., Saupe, D. (2013). Chaos and
Fractals: New Frontiers of Science. New York:
Springer-Verlag.
Perlin, K., Hoffert, E.M. (1989). Hypertexture. ACM
SIGGRAPH Computer Graphics. 23 (3). 253-262.
https://doi.org/10.1145/74334.74359.
Petrov, St. (2020). 3D-Fractal-Mandelbulb-Raymarching.
https://github.com/StanislavPetrovV/3D-Fractal-Mand
elbulb-Raymarching. (Accessed 10 November 2024).
Prusinkiewicz, P., Lindenmayer, A. (1990). The
Algorithmic Beauty of Plants, Springer-Verlag New
York Inc. 1990. Author’s electronic version of this
book with corrected errors: http://algorithmic
botany.org/ (Accessed 15 May 2024).
Quan, L., Tan, P., Zeng, G., Yuan, L., Wang, J., Kang, S.B.
(2006). Image-Based Plant Modeling. ACM Trans.
Graph. (TOG), 25 (3), 599-604. https://doi.org/10.11
45/1141911.114192.
Quilez, I. (2013). Smooth minimum for SDFs.
https://iquilezles.org/articles/smin/. (Accessed 11
January 2025).
Random Trees (2021). Random Trees, Tree images for
training model. https://www.kaggle.com/datasets/
ambitiondream/random-trees?resource=download.
(Accessed 28 November 2024).
Requicha, A.A.G., Voelcker, H.B. (1977).Constructive
solid geometry. Tech. Memo. 25, Production
Automation Project, Univ. Rochester, Rochester, N.Y.,
Nov 1977.
Raymarching (2016). Raymarching Distance Fields:
Concepts and Implementation in Unity.
https://adrianb.io/2016/10/01/raymarching.html.
(Accessed 10 November 2024).
Reche-Martinez, A., Martin, I., Drettakis G. (2004).
Volumetric reconstruction and interactive rendering of
trees from photographs. ACM Trans. Graph. (TOG) 23,
(3), 720-727. https://doi.org/10.1145/1015706.101578.
Semrau, A. and Sawicki, D. (2024). Efficiency of 3D
Fractal Generation Through Raymarching. In
Proceedings of the 19th International Joint Conference
on Computer Vision, Imaging and Computer Graphics
Theory and Applications (VISIGRAPP 2024), 252-260.
https://doi.org/10.5220/0012380500003660.
Shadertoy, (2013). Shadertoy https://www.shadertoy.com/
about (Accessed 20 November 2024).
Stava, O., Pirk, S., Kratt, J., Chen, B., Mech, R., Deussen,
O., Benes, B. (2014). Inverse Procedural Modelling of
Trees. Computer Graphics Forum. 33 (6), September
2014, 118-131. https://doi.org/10.1111/cgf.12282.
Tan, P., Zeng, G., Wang, J., Kang, S.B., Quan, L. (2007).
Image-based tree modeling. ACM Trans. Graph.
(TOG), 26, (3), 87-es. https://doi.org/10.1145/12763
77.1276486.
Tan, P., Fang, T., Xiao, J., Zhao, P., Quan, L. (2008). Single
Image Tree Modeling. ACM Trans. Graph. (TOG), 27
(5), Article 108 (2008), 1-7.
https://doi.org/10.1145/1409060.14090.
Tuy, H. and Tuy, L. (1984). Direct 2-D Display of 3-D
Objects. IEEE Computer Graphics and Applications. 4
(10), 29-34. https://doi.org/10.1109/MCG.1984.64293
33.
Unity, (2024). Unity official website. https://unity.com/
(Accessed 19 November 2024).
Unreal Engine, (2024). Unreal Engine official website.
https://www.unrealengine.com/ (Accessed 19
November 2024).
Walczyk, M. (2023). Ray Marching. https://michael
walczyk.com/blog-ray-marching.html (Accessed 10
November 2024).
Wong, J. (2016). Ray Marching and Signed Distance
Functions. https://jamie-wong.com/2016/07/15/ray-
marching-signed-distance-functions/. (Accessed 10
November 2024).
XenoDream Software, https://www.xenodream.com.
(Accessed 4 November 2024).
Xiao, Z., Jiang, H., Deng, Z., Li, R., Han, W., Wang, Z.
(2024). Large Scale Farm Scene Modeling from
Remote Sensing Imagery. ACM Trans. Graph. (TOG).
43(6). Article No. 260, 1-12. https://doi.org/10.1145/
3687918.
GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications
384