Integration of On-Demand Ride-Pooling into a Microscopic Traffic

Flow Simulation Environment

Oytun Arslan

and Silja Hoffmann

Chair of Intelligent, Multimodal Transport Systems, University of the Bundeswehr Munich, Werner-Heisenberg-Weg 39,

Munich, Germany

Keywords: On-Demand Mobility, Ride-Pooling, Microscopic Traffic Flow Simulation, Matching Algorithms.

Abstract: The aim of this study is to model an on-demand ride-pooling system in a microscopic traffic flow simulation

environment. On-demand systems are hardly modeled in microsimulations, hence a research gap was

identified here. First of all, a methodology was developed to match the requests with the vehicles, considering

the operator as well as the passenger interests. Then the simulation setup for the campus of the University of

the Bundeswehr Munich was carried out, taking into account the specialties for on-demand traffic and the

traffic data feed for the remaining traffic. The data flow from already installed traffic cameras into the

microsimulation was illustrated and the steps to model on-demand traffic were elaborated. Results have shown

that the objective function can be modified according to the ride-pooling system requirements via various

weighting parametrizations, that higher demand profiles lead to more shareability and efficiency, and that

ride-pooling strategy outperforms ride-hailing in on-demand systems.

1 INTRODUCTION

Due to the increase in the urban population, recent

years have brought many innovative ideas regarding

mobility concepts. One of the new paradigms is the

sharing concept, where users share the vehicles

instead of owning them.

In conventional public transportation, the

timetables and departure times are fixed. In addition,

the route of the public transport vehicle is also fixed,

so transfers between vehicles to reach from origin to

destination are not rare. This rigidness leads to a user

dissatisfaction, which is why new flexible shared on-

demand concepts were developed, such as ride-

hailing and ride-pooling. Uber, Lyft, Bolt and MOIA

(Germany) are currently well-known companies that

invest in these new ideas. Both in ride-hailing and

ride-pooling, users can send requests for a trip by

typically stating the origin and destination, and when

to ride. In ride-hailing, trips are not shared, i.e., an

exclusive trip for the user, very similar to a taxi

system. In ride-pooling, on the other hand, trips may

be shared (pooled) if there is a certain similarity

between them, such as similar route and similar

https://orcid.org/0000-0002-5221-4698

https://orcid.org/0000-0002-0499-0342

departure times. Finding out pooling potentials by

individual drivers is not practical, therefore a central

dispatching system collects the requests and decides

which requests to be pooled together in which

vehicle.

It is obvious that the dispatching algorithm is the

core essence of such a ride-pooling platform. The two

sides of such a system are a) the operator with its

vehicles, the aim is to realize its service with as less

mileage as possible; b) the users which appear in the

system as trip requests, the aim is to have less waiting

times at the departure and less detour times caused by

pooling.

This paper focuses on the ride-pooling

dispatching algorithm and develops a methodology

for optimally assigning requests to vehicles in a

dynamic manner. The platform to model the ride-

pooling system was chosen as the microscopic traffic

flow simulation (microsimulation) Vissim (PTV,

2024). Microsimulations are widely used in traffic

engineering for assessing and planning road

infrastructures, evaluation of traffic management

measures as well as testing new technologies and

systems (Daamen et al., 2015). However, on-demand

506

Arslan, O. and Hoffmann, S.

Integration of On-Demand Ride-Pooling into a Microscopic Trafﬁc Flow Simulation Environment.

DOI: 10.5220/0013341400003941

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 506-513

ISBN: 978-989-758-745-0; ISSN: 2184-495X

systems are hardly modeled in microsimulations as

will be mentioned in the next chapter, and this has

pointed out a research gap in this area. Closing this

gap will mean that it will be possible to add on-

demand modes in microsimulation models (where

motorized, bicycle and pedestrian traffic are already

present) in the future (Arslan and Hoffmann, 2024a).

2 LITERATURE REVIEW

Ride-pooling belongs to dial-a-ride-problems

(DARP), which is a sub-topic of vehicle routing

problems (VRP). In the literature, the problems are

divided into two main parts: either static or dynamic

(Pillac et al., 2013; Psaraftis et al., 2016; Ho et al.,

2018; Ghandeharioun and Kouvelas, 2023). In static

problems, all the input data are known before the

calculation of routes. If an operator gets a list of trip

requests with origin, destination and desired

departure time in advance, this can be classified as a

static problem. Cordeau (2006) solved such a static

DARP problem with 48 requests using a branch and

cut algorithm. Armellini (2021) used SUMO

microscopic simulation tool to assign 55 requests to

vehicles in Brunswick, Germany in a static manner.

Dynamic problems occur if the input data is not fully

known, e.g., if new requests arrive to the system

during the transportation of current requests.

Assignment of new requests causes the change of

current routes of vehicles, so there is a dynamic

aspect in terms of decision making. Pillac et al. (2013)

gave an overview about current algorithms in

dynamic VRP. Building upon this work, Psaraftis et

al. (2016) extended the review also for dynamic

DARP. In the literature, there are also some papers

which reviewed both static and dynamic DARP

problems (Cordeau and Laporte, 2007; Ho et al.,

2018).

To test the ride-pooling algorithms, different

modelling environments have been used until now.

For example, Friedrich et al. (2018) and Thomsen

(2023) used Visum macroscopic simulation for this

purpose. Yet, most of the work here was conducted

with agent-based simulations, for instance with the

open-source agent-based simulation tool MATSim

(Fagnant and Kockelman, 2018; Narayan, 2020) or a

self-developed agent-based simulation tool FleetPy

(Engelhardt et al., 2022).

Regarding microscopic traffic simulation, Dandl

(2017) used Aimsun to implement an autonomous

taxi system in Munich, however only with ride-

hailing. Armellini (2021) as well as Tang and

Armellini (2021) used SUMO microsimulation, but

only in the static DARP context, the latter

implemented without ride-pooling.

As a conclusion to this literature review, it has

been clear to the authors that a research gap could be

identified concerning a dynamic DARP

implementation for ride-pooling in microscopic

traffic simulation.

3 MATCHING METHODOLOGY

In a ride-pooling system, users send their trip requests

via a smartphone to a central dispatcher. The requests

typically include the trip origin, trip destination and

the desired departure time. If the user wants to realize

his/her trip as soon as possible, this is regarded as an

immediate request, which is most of the time the case.

The central dispatcher monitors the fleet and matches

the incoming requests with the appropriate vehicles

based on certain criteria. In this chapter, such a

matching algorithm with essential parameters will be

elaborated.

The methodology here is built upon the previous

study of Arslan and Hoffmann (2024b), which we

refer to for the main features and the further details.

3.1 Creating Valid Permutations

Every time a new request arrives in the system, it will

be checked which vehicle can take it over. Since

vehicles are already moving in the simulation to pick-

up/drop-off previous requests, their current status

must be also taken into account when calculating the

possible options for the new request. If for instance a

new request (X) arrives in the system, and at that

moment the status of a regarded vehicle is as follows:

2 requests (A and B) are already picked-up and

travelling in that vehicle, 1 request (C) is recently

assigned to this vehicle but not yet picked-up, all

possibilities of a permutation of 6 points (these are

, B

, C

, X

where the indices are P: pick-

up, D: drop-off) have to be considered. For each

permutation, a route legitimacy check needs to be

carried out, i.e., checking whether the drop-off point

of a request happens not before its pick-up point.

Assuming that i is the number of in-vehicle

passengers in a vehicle and t is the number of requests

to be picked up by a vehicle, a general formula for the

number of valid permutations to transport the in-

vehicle passengers, to-be-picked-up passengers as

well as the new request can be stated as:

𝑇𝑜𝑡𝑎𝑙 𝑛𝑜. 𝑜𝑓 𝑝𝑒𝑟𝑚𝑢𝑡𝑎𝑡𝑖𝑜𝑛𝑠 =



𝑖+2𝑡+2





(1)

Integration of On-Demand Ride-Pooling into a Microscopic Trafﬁc Flow Simulation Environment

507

According to this formula, the above example

(i=2 and t=1) leads to 180 permutations in total. Then

another check regarding the vehicle capacity must be

conducted in order to avoid an excess of capacity in

any permutation, since vehicles might exploit their

capacity values by incorporating the new request in

their travel plans. Here, if the number of requests

inside the vehicle is more than its capacity at any

point of time, the concerned permutation will be

omitted.

Following examples illustrate the generation of

valid permutations for the vehicle mentioned above,

assuming a vehicle capacity of 3:

• A

 X

 C

 X

 B

permutation is not valid since drop-off of X

) happens before its pick-up (X

• C

 X

 B

 X

 C

 A

permutation is not valid since the number of

requests inside the vehicle goes up to 4 after

the pick-up of X (X

), hence exceeds the

vehicle capacity of 3.

• B

 X

 C

 X

 A

permutation is valid since route legitimacy is

guaranteed and vehicle capacity is never

exceeded.

3.2 Filtering out Permutations

Among valid permutations, another filtering

mechanism is used in terms of waiting times and

detour ratios of passengers. Here maximum waiting

time is the maximum acceptable time for a passenger

to be picked-up after sending a request. Detour ratio

is the ratio of the actual travel time (increased due to

pooling) to the direct travel time. Permutations

resulting in high waiting times or detour ratios are

cancelled out since they are not acceptable for

passengers at all, even if the permutation globally

turns out to have a good overall score. These values

are parameters in the case studies.

3.3 Calculation of Overall Score

The procedure mentioned above is applied to all

vehicles in the system in order to create a pool of valid

vehicle-permutation combinations. The aim is then to

find the best solution from this pool. For this, both the

passenger’s point of view and the operator’s point of

view are analyzed. While operators try to diminish the

total vehicle travel times, passengers have mainly two

discouragements in ride-pooling: i) waiting time for

the vehicle, ii) detour time due to pooling, equal to the

in-vehicle time minus the direct trip time. While the

in-vehicle passenger suffers only from the latter, the

new request and the to-be-picked-up passenger suffer

from both, depending on the situation. A new

assignment causes a change in the route and stop

sequence of the vehicle. This affects the remaining

tour time of the vehicle as well as the waiting and

detour times of the passengers currently planned in

the tour of a vehicle.

An overall score of an option can therefore be

formulated as follows:

(2)

where tt

is the planned tour time of the vehicle v,

is the waiting time and dt

is the detour time of the

request r, all for either the current status or the new

status of the system. W

and W

are the weightings for

operator side (vehicle time) or passenger side

(waiting time and detour time). veh and req are the

sets of vehicles and requests respectively, that are

present in the simulation at the decision time. The

first part of the formula represents the extra travel

time of vehicles after a new request is assigned,

whereas the second part represents the extra time

burden of requests. By adoption of weightings, more

emphasis can be put on either side, which brings a

certain design flexibility.

In the next step, the overall score is calculated for

all possible permutations. The permutation with the

least value of the overall score is used for the

assignment, the new request will be matched to the

vehicle associated with that permutation.

4 SIMULATION SETUP

The matching algorithm was applied in a Vissim

microscopic simulation of the University of the

Bundeswehr Munich campus. The simulation

incorporates on one side the on-demand ride-pooling

shuttles, on the other side the remaining campus

traffic with other transport modes. The campus has an

area of 140 hectares and consists of many facilities

fulfilling different purposes such as various research

buildings, administrative buildings, a university

library, dormitories, a post office, sports facilities,

sanitary facilities, a kindergarten, and a canteen. 16

shuttle stops were decided based on the campus

entry/exit points, surveys conducted among

university members and the most important campus

locations (Figure 1). Moreover, a depot was

implemented for the shuttles where they all start the

simulation at the beginning. During the simulation, in

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

508

case shuttles did not have any new task, they waited

at the last stop in the idle mode. Only when a stop was

occupied by a shuttle while another one wanted to

approach there i.e., due to drop-off of a request, the

former shuttle was sent to the depot to make room for

the latter. Since the demand profile showed an even

distribution within the campus and the area of campus

is not too large, no rebalancing or relocation strategies

were applied in this study.

Figure 1: Campus of the University of the Bundeswehr

Munich with 16 shuttle stops shown in red circles and X as

depot. Diamonds show the important spots in the campus.

Green: Main entrance, Purple: Sport facilities, Black:

Laboratories, Brown: Library, Blue: Canteen (Source:

OpenStreetMap).

4.1 Simulation Setup for the

Remaining Campus Traffic

For the simulation data feed, the available camera

data in the campus as well as manual traffic counts

were used. Within the scope of the MORE project

(MORE, 2024), traffic data collection cameras were

installed in the university campus. These cameras can

detect different vehicle types and can provide

historical count data around-the-clock. Camera data

are sent via LAN/WLAN to a first server, where

operators can set virtual gates on the camera images

for various vehicle types via a client. 13 different

vehicle types were used for the simulation, including

car, truck, bicycle and pedestrian. Gates produce

counts for every previous minute and these are sent to

a central back-end server via webhooks, where all

traffic data of the campus within the MORE project is

stored. Afterwards, the simulation queries the camera

data for a specific date and time via an API. Here, the

COM interface of Vissim is used to realize such

queries. An overview of the data flow is illustrated in

the following figure.

Figure 2: Data flow diagram for the remaining campus

traffic.

The objects in Vissim that are updated via camera

data are listed as follows:

• Vehicle inputs: Starting point of vehicles.

Involves counts and vehicle compositions,

both per time interval.

• Vehicle compositions: Modal split of

traffic. Involves vehicle types and relative

values. Used in vehicle inputs.

• Route decisions: Decision points for

vehicles at intersections. Involves vehicle

types and routes.

• Routes: Turning directions at intersections.

Involves direction and relative values per

time interval.

Since there was not sufficient coverage of traffic

cameras in the whole campus, it was inevitable to

conduct manual traffic counts as well. Here, traffic

streams were counted for every 15 minutes for certain

vehicle types (car, heavy, motorcycle, bicycle,

scooter, pedestrian). Based on the 7 traffic count

spots, missing vehicle inputs and compositions were

generated. Moreover, based on 11 traffic count spots,

missing route decisions and routes were generated.

Since manual traffic counts were not practical for

long time periods, extrapolations and assumptions

were used where no count data existed.

Calibration of the simulation was performed in

two steps. In the first step, the travel times were

calibrated by doing test trips in the real world and

sending probe vehicles in the simulation (Daamen et

al., 2015). These values were compared for two main

routes in the campus, for both directions. According

to the results, the stoppage time at the barriers (used

for controlled access into the campus and within the

campus in certain areas) were adopted in the

simulation. As a second step, vehicle speeds were

calibrated using the camera data. At 8 camera spots,

car speeds were filed in .csv format for 7-9 a.m.

morning peak time. For each spot, a cumulative speed

distribution was created in the simulation. These

distributions were then incorporated with desired

speed decisions object in the simulation, upstream of

Integration of On-Demand Ride-Pooling into a Microscopic Trafﬁc Flow Simulation Environment

509

that spot. Within the calibration process, the

distributions were fine-tuned to achieve a good

fitness. At the end of the calibration process, it could

be confirmed by statistical t-tests that both datasets

could fit to each other for all the 8 spots.

4.2 Simulation Setup for the on-

Demand Shuttle Traffic

Standard microsimulation functionalities are not

sufficient to gather the peculiarities of on-demand

systems, since vehicles mainly get a static route at

intersections or the origin-destination routes assigned

to a vehicle at the beginning of the simulation does

not change during the simulation run. In on-demand

shuttle case, however, these properties are necessary

since vehicles have to get dynamic routes and be able

to change their route “on the fly” in case of the new

system triggers, such as an incoming request. Vissim

does not offer a standard solution for on-demand

vehicles, nevertheless, it offers an external

programming via the COM interface. With this

interface, codes such as in python can be applied to

the model, enabling control of the system externally.

Some modifications and adoptions in the simulation

were necessary to get the on-demand features, to

name a few:

• The option “dynamic assignment” was

activated

• Whole network was furnished with nodes

and edges, relating to the graph theory

• Shortest routes between the nodes were

calculated by Dijkstra’s shortest path

algorithm (Gkiotsalitis, 2022)

• Shuttle stops were modelled as one-vehicle

parking lots where a usage for dynamic

assignment was activated

• Priority rules were used at shuttle stops to

make a shuttle wait at the right spot if the

stop is occupied by another shuttle

• Nodes were categorized as allowed/

disallowed for shuttles in order to be able to

control the nodes and edges where a shuttle

could travel (since some road sections in the

campus were not meant for the shuttle

usage)

• Vehicle attributes were extended with new

ones, such as vehicle status, average

occupancy, empty drive kilometer, idle time,

planned vehicle path

• Request attributes were created such as

request status, direct trip distance, request

time, real pick-up time, real drop-off time

• A function sending an idle shuttle to its

depot if it blocks another shuttle was applied

in python code

• A function to export certain KPIs to a .csv

file for further analysis was applied in

python code

Another essential point in the on-demand

simulation is generating a request pool. In order to

mimic the on-demand travel demand of passengers

within the university campus, the microsimulation

had to be fed with trip requests. Since the campus has

its own peculiarities, e.g. certain origin-destination

pairs are more prevalent depending on the time of the

day, usage of a realistic dataset was deemed

necessary. Therefore, the trip base of the

micromobility sharing system of the campus was

utilized. This platform, known as MORE Sharing, is

operated on a free-floating system and enables users,

who are solely the university members, to book e-

scooters, e-bikes, e-cargo bikes, city bikes and e-

mopeds for their trips (MORE, 2024).

The sharing data was analysed from the system

launch (06.03.2023) until 05.11.2023, for an 8-month

period. For the shuttle system demand, the day with

the highest demand is taken as base, which is

21.03.2023. Since the travel demand on that day

before 7 a.m. was very scarce, only trips after 7 a.m.

until midnight were considered. This led to a

simulation run of 17 hours in total for 385 trip

requests.

4.3 Workflow of Simulation

The microsimulation gathers all the inputs mentioned

in the previous parts, and starts running for 17 hours.

During the course of the simulation, incoming

requests trigger the simulation to do new calculations

and the “optimum” vehicles are matched with those

requests one-by-one (or requests are rejected),

vehicles are sent to different locations according to

their assignments and finally, the simulation delivers

outputs for the analysis.

5 RESULTS

Regarding the camera data, it was important to select

a day within the lecture time periods. The campus

traffic at the weekends is also quite low, that is why a

weekend day was avoided. For these reasons, a

typical weekday was chosen (16.10.2024 Monday).

Other required parameters in the simulation runs are

as follows: Simulation period is 17 hours (7 a.m. until

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

510

midnight), boarding/alighting time for the shuttles is

30 seconds, shuttle maximum speed is 15 km/h

(autonomous shuttle assumed), request pool is 385

requests based on MORE Sharing, and simulation

resolution is 3 time-steps per simulation second. The

chosen operational parameters will be given in detail

in the scenario descriptions below.

5.1 Impact of Weightings in the

Overall Score

In this analysis, the idea was to depict the impact of

and W

values (the weightings) in Equation 2 on

the certain metrics of the system.

For this analysis, a fleet size of 4 vehicles with a

capacity of 4, a maximum waiting time of 10 minutes

and a maximum detour ratio of 2 were assumed.

Three scenarios were prepared, one with the same

weightings for operator and passenger side, second

one with operator side dominant (5 to 1) and the last

one with passenger side dominant (1 to 5).

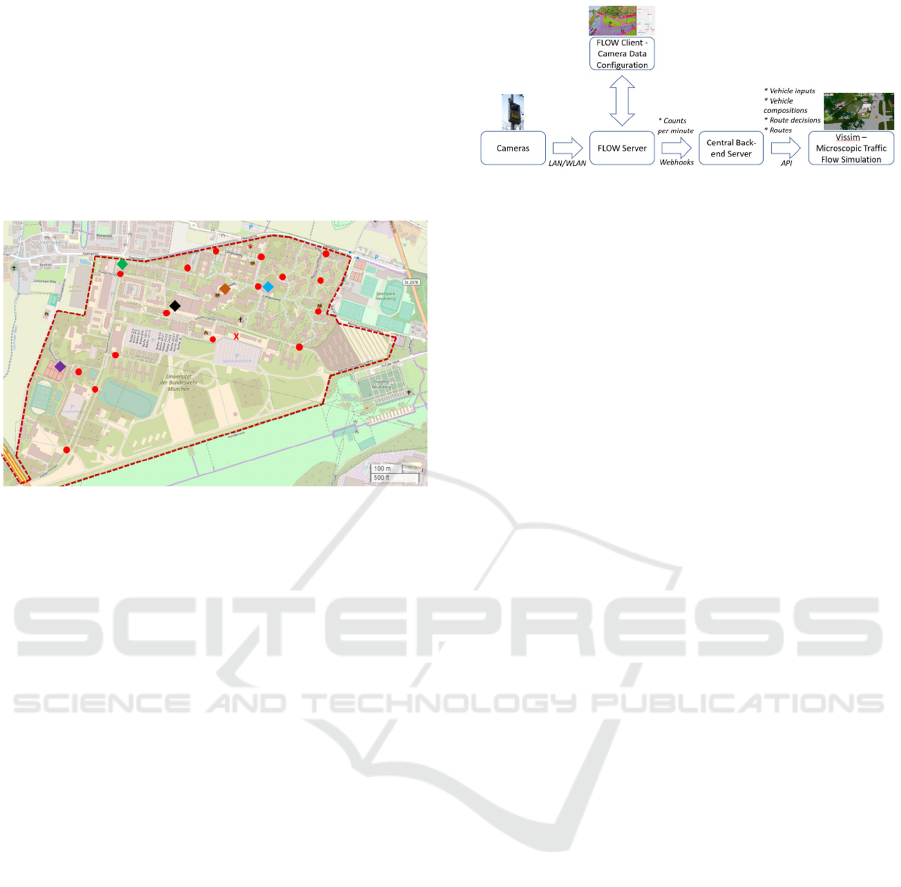
It can be seen from the Figure 3 that mean mileage

of the shuttles diminish when operator side is more

emphasized (W

vs W

). In this case, mean

waiting and detour time increase, which shows the

disadvantage for passenger side. The total delay,

which is the waiting time plus the detour time also

increases. On the other hand, if the passenger side is

more emphasized (W

vs W

), the effect is

the other way around: the mileage increases whereas

the passenger burdens (waiting and detour time)

decrease. Here, the waiting time experiences a very

slight decrease (2%) yet the detour time decrease is

around 30%. As an additional remark to the readers,

it was observed that the percentage of the served

requests remained almost the same for all three

scenarios.

With this analysis, it is demonstrated that the

objective function (the overall score) can be modified

according to the needs of the ride-pooling system via

various weighting parametrizations.

5.2 Impact of Travel Demand

In this analysis, the travel demand for on-demand

shuttles in the campus was increased gradually in

order to observe its impacts on the system metrics. As

in the previous analysis, a fleet size of 4 vehicles with

a capacity of 4, a maximum waiting time of 10

minutes and a maximum detour ratio of 2 were

assumed. The first scenario involves the default

demand extracted from the MORE Sharing. In the

second scenario, amount of this demand was doubled

and in the third tripled. The new demand was

Figure 3: Impact of weightings (W

and W

) in the overall

score.

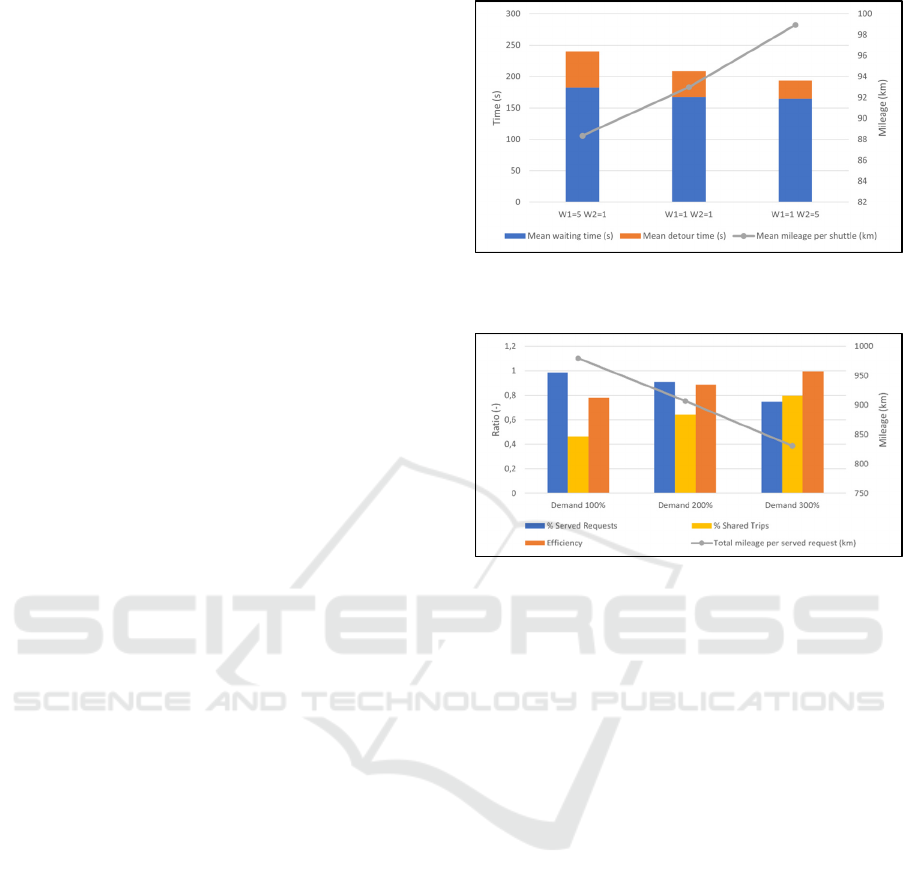
Figure 4: Impact of travel demand on certain system

metrics.

produced randomly in terms of start location, end

location and start time.

Figure 4 underlines that higher demand cannot be

satisfied fully anymore: With 100% demand, the

percentage of served requests are almost 1 (nearly no

request had to be rejected), whereas this metric

reduces down to 0,9 and 0,75 if the travel demand is

increased. A way to mitigate this effect could be to

increase the fleet size.

Shared trips are defined as the number of requests

who share a ride, divided by the total number of

served requests. The percentage of the shared trips

increase with increasing demand since a larger

request pool has a positive effect on the shareability,

therefore more requests can be pooled together.

Efficiency is defined as the direct trip distances of

served requests (benefit) divided by the total mileage

(cost) (Liebchen et al., 2020). Normally, it is expected

that more shareability, i.e., more pooling has a

positive impact on the efficiency. This can be

confirmed with the results: From lowest demand to

the highest, there is a gradual increase of efficiency.

Even with triple demand, the efficiency is very close

to 1, which means the costs are as much as the

benefits. Certainly, with higher demand and other

Integration of On-Demand Ride-Pooling into a Microscopic Trafﬁc Flow Simulation Environment

511

fleet size constellations, an efficiency higher than 1

can be reached.

Lastly, a glance at the total mileage per served

request implies that less mileage per served request is

required in higher demand scenarios: 15% less in

triple demand scenario compared to the normal

demand.

With this analysis, it can be inferred that a more

efficient system can generally be reached with higher

demand profiles, since the pooling effect becomes

then more visible.

5.3 Comparison of Ride-Hailing and

Ride-Pooling

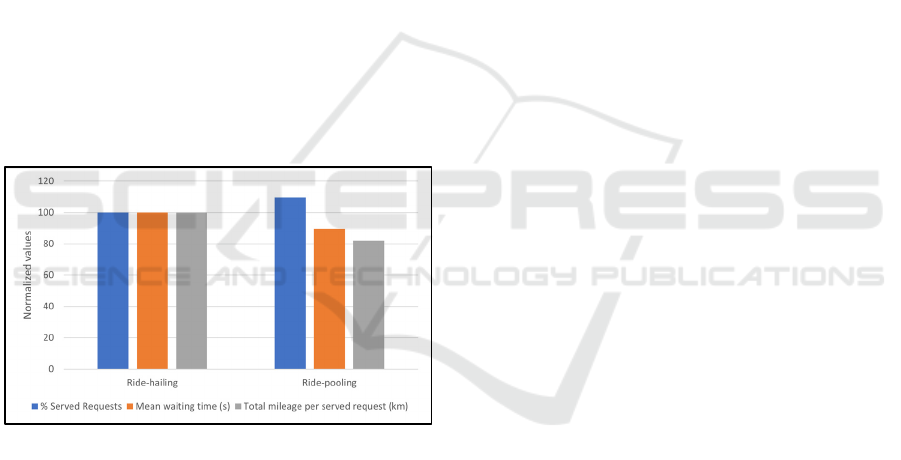
In this analysis, the ride-pooling strategy was

compared to the ride-hailing. In ride-hailing, trips are

not shared so each trip is conducted exclusively.

Here, 4 vehicles with capacity 1 (ride-hailing) and 4

(ride-pooling) were used. Moreover, a maximum

waiting time of 5 minutes and a maximum detour

ratio of 2 were assumed. To perceive the impact

better, the three metrics used were normalized for the

ride-hailing case to 100 units. The comparison can be

viewed in the following figure:

Figure 5: Comparison of ride-hailing and ride-pooling.

Here, the pooling strategy contributes almost 10%

in terms of served requests. Also, in terms of mean

waiting time of passengers, there is a decrease of 10%

when pooling is performed. Finally, the total mileage

per served request is decreased by nearly 20% with

pooling. It can therefore be concluded that a pooling

strategy with a well-established matching algorithm

has immense positive impacts on the on-demand

system.

6 CONCLUSIONS AND FUTURE

WORK

This study aims to model a ride-pooling system in a

microscopic traffic flow simulation environment. A

comprehensive literature review showed that there is

a research gap here for microsimulations. For this,

firstly a methodology was developed to match the

requests with the vehicles. Both operator and

passenger side were considered in the decision

function, moreover weightings were used to make

more emphasis on either side. Then the simulation

setup for the campus of the University of the

Bundeswehr Munich was carried out, taking into

account the specialties for on-demand traffic as well

as the traffic data feed for the remaining traffic. Here

camera data and manual traffic count data were

utilized, the latter in case camera data were not

available at certain slots. Furthermore, on-demand

requests were extracted from the micromobility

sharing system of the campus.

Different scenarios were simulated to explore the

impacts of weightings in the overall score, impact of

amount of demand, and impact of ride-pooling

strategy compared to ride-hailing on the certain

system metrics. Results have shown that i) the

objective function can be modified according to the

needs of the ride-pooling system via various

weighting parametrizations, ii) higher demand

profiles lead to more shareability and efficiency, and

iii) ride-pooling strategy outperforms ride-hailing in

on-demand systems.

In a future research work, a different assignment

algorithm will be applied, namely batch assignment,

where the requests are assigned to vehicles in certain

batches (time periods), rather than immediately. This

can lead to more efficient matches since the search

space is then greater, as suggested by the literature.

In the current algorithm, the shortest paths are

calculated based on the distance between nodes.

However, an ideal approach would be considering the

traffic situation as well. As an advantage of the

microsimulation tool, the current traffic situation can

be extracted, analyzed and the weightings of the

edges can be modified accordingly, leading for

instance to a more expensive edge in case of

congestion. In this way, the Dijkstra algorithm can be

forced to find less congested connections instead of

the shortest ones, which can again be a topic for

further research.

The case study was conducted in a university

campus within the scope of a campus research

project. Due to the scarce travel demand and small

service area, a small fleet was used. Another further

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

512

research point would be the scalability of this study

to larger urban areas. First, setting up the

microsimulation model for a larger area will certainly

be more intricate. Here, depending on the objective of

the model, the level of detail needs to be determined

carefully. Furthermore, a larger area implies having

more travel demand and a larger fleet size, hence

more frequent matchings. The impact of this on the

simulation performance must be then cautiously

investigated.

ACKNOWLEDGEMENTS

This research is funded by dtec.bw – Digitalization and

Technology Research Center of the Bundeswehr. The

dtec.bw is funded by the European Union –

NextGenerationEU.

REFERENCES

Armellini, M.-G. (2021). A Tool for Simulating Demand

Responsive Transport System in SUMO. In 7th IEEE

International Conference on Models and Technologies

for Intelligent Transportation Systems (MT-ITS), pp.

425-429.

Arslan, O. and Hoffmann, S. (2024a). Implementation of a

spontaneous matching algorithm for on-demand shuttle

systems in microsimulation. Transportation Research

Procedia 78 pp. 418–427.

Arslan, O. and Hoffmann, S. (2024b). Impacts of On-

Demand Shuttle System Parameters on its Metrics: A

Microsimulation Study. In 26th Euro Working Group

on Transportation Meeting (EWGT 2024), Lund,

Sweden.

Cordeau, J.-F. (2006). A Branch-and-cut algorithm for the

dial-a-ride problem. Operations Research, 54, 573–586.

Cordeau, J.-F. and Laporte, G. (2007). The Dial-a-ride

Problem (DARP): Models and Algorithms. Annals OR,

vol. 153, pp. 29–46.

Daamen, K., Buisson, C., Hoogendoorn, S. (2022). Traffic

Simulation and Data – Validation Methods and

Applications. International Standard Book Number-13:

978-1-4822-2871-7 (eBook - PDF). CRC Press

Publications, USA.

Dandl, F., Bracher, B. and Bogenberger, K. (2017).

Microsimulation of an Autonomous Taxi-System in

Munich. In 5th IEEE International Conference on

Models and Technologies for Intelligent Transportation

Systems (MT-ITS), pp. 833–838.

Engelhardt, R., Dandl, F. and Bogenberger, K. (2022).

FleetPy: A Modular Open-Source Simulation Tool For

Mobility On-Demand Services. Available at

https://arxiv.org/pdf/2207.14246.pdf.

Fagnant, D. J. and Kockelman, K. M. (2018). Dynamic

Ride-Sharing and Fleet Sizing for a System of Shared

Autonomous Vehicles in Austin, Texas. Transpor-

tation, Vol. 45, 2018, pp. 143–158

Friedrich, M., Hartl, M. and Magg., C. (2018). A Modeling

Approach for Matching Ridesharing Trips Within

Macroscopic Travel Demand Models. Transportation,

Vol. 45, No. 6, 2018, pp. 1639–1653.

Ghandeharioun, Z. and Kouvelas, A. (2023). A survey of

dial-a-ride problems: Literature review and recent

developments. Transportation Research Part C. Vol

151.

Gkiotsalitis, K., (2022). Public Transport Optimization.

ISBN 978-3-031-12443-3. Springer Publications,

Switzerland.

Ho, S.C., Szeto, W., Kuo, Y.-H., Leung, J.M., Petering, M.

and Tou, T.W. (2018). A survey of dial-a-ride

problems: Literature review and recent developments.

Transportation Research Part B. Vol 111, pp 395-421.

Liebchen, C., Lehnert, M., Mehlert, C. and Schiefelbusch,

M. (2020). Ridepooling-Effizienz messbar machen. In

Nahverkehr 09/2020, pp 18-21.

MORE Mobility Research. (2024). MORE Mobility

Research Project für die Universität der Bundeswehr.

Narayan, S. (2020). Design and Analysis of On-Demand

Mobility Systems. Dissertation in Delft University of

Technology.

Pillac, V., Gendreau, M., Gueret, C. and Medaglia, A.L.

(2013). A Review of Dynamic Vehicle Routing

Problems. European Journal of Operational Research

225(1): 1-11.

Psaraftis, H., Wen, M. and Kontovas, C. (2016). Dynamic

Vehicle Routing Problems: Three Decades and

Counting. NETWORKS, Vol. 67(1), 3–31.

PTV AG. (2024). VISSIM Version 2024. Karlsruhe,

Germany: Available at https://www.ptvgroup.com/de/

loesungen/produkte/ptv-vissim/.

Tang, Q. and Armellini, M.-G. (2021). An Ant Colony

Algorithm with Penalties for the Dial-a-ride Problem

with Time Windows and Capacity Restriction. In 7th

IEEE International Conference on Models and

Technologies for Intelligent Transportation Systems

(MT-ITS), pp. 425-429.

Thomsen, N. (2023). Implementing a Ride-sharing

Algorithm in the German National Transport Model

(DEMO). Transportation Research Record: Journal of

the Transportation Research Board, Vol. 2677(5), 1–10.

Integration of On-Demand Ride-Pooling into a Microscopic Trafﬁc Flow Simulation Environment

513