Graphical Analysis of Abstract Argumentation Frameworks via Boolean
Networks
Van-Giang Trinh
1
, Belaid Benhamou
2
and Vincent Risch
2
1
Inria Saclay, EP Lifeware, Palaiseau, France
2
LIRICA Team, LIS, Aix-Marseille University, Marseille, France
Keywords:
Abstract Argumentation Framework, Extension-Based Semantics, Graphical Analysis, Boolean Network.
Abstract:
Abstract Argumentation Frameworks (AFs) are the key formalism of abstract argumentation, which is one of
the main directions in argumentation research. An AF is mainly studied by means of its extensions, defined
as subsets of arguments. In this work, we define a Boolean Network (BN) encoding for AFs, where BNs
are a simple and efficient mathematical formalism that has a long history of research. We then show that the
attack graph of an AF coincides with the influence graph of its encoded BN, and in particular preferred and
stable extensions of this AF one-to-one correspond to minimal trap spaces and fixed points of the encoded
BN, respectively. We also define a new concept for BNs called complete trap space, then show that complete
trap spaces (resp. the percolation of the special trap space where all variables are free) in BNs one-to-one
correspond (resp. corresponds) to complete extensions (resp. the grounded extension) in AFs. This connection
opens the promising application to graphical analysis of AFs, which is an interesting line of research with
many useful applications. More specifically, we use it to explore many new results relating extensions of an
AF and (positive or negative) cycles in its attack graph. In particular, we show new upper bounds based on
positive feedback vertex sets for the numbers of stable, preferred, and complete extensions.
1 INTRODUCTION
Abstract Argumentation Frameworks (AFs) are the
key formalism of abstract argumentation, which is
one of the main directions in argumentation re-
search (Toulmin, 1958; Pollock, 1987; Pollock,
1991b; Pollock, 1991a; Dung, 1995; Baroni et al.,
2020). An AF models arguments as vertices in a di-
rected graph, where a directed arc denotes an attack
from the starting vertex to the ending vertex, provid-
ing a graphical representation. The main concept to
study AFs is an extension defined as a subset of argu-
ments. There are many different types of extension-
based semantics in AFs (Baroni et al., 2020). Among
others, stable, preferred, grounded, and complete se-
mantics are first proposed in Dung’s 1995 seminal pa-
per. Nowadays, they still play a central role in ar-
gumentation research and attract much attention from
not only the argumentation community but also other
research communities (Baumann and Strass, 2013;
Thimm et al., 2021; Obiedkov and Sertkaya, 2023;
Dimopoulos et al., 2024).
Regarding the analysis of AFs, there are two
main directions of research. In practice, a vari-
ous number of interesting computational problems
w.r.t. extensions have been proposed and studied for
decades (Charwat et al., 2015). Notable ones in-
clude 1) deciding a given argument appears in at least
one extension (resp. all extensions) of a certain type,
i.e., credulous (resp. skeptical) reasoning (Thimm
et al., 2021), 2) enumerating extensions of a certain
type (Kr
¨
oll et al., 2017), and 3) counting the num-
ber of all extensions of a certain type, which is also a
direct consequence of the enumeration problem (De-
woprabowo et al., 2022). To address these problems,
many methods have been proposed, exploiting promi-
nent techniques in symbolic AI such as answer set
programming, SAT, and constraint programming, or
techniques from other fields such as graph theory and
formal concept analysis.
In theory, it is interesting and crucial to find graph-
ical conditions for properties on extensions of an AF.
For example, several studies (Baumann and Strass,
2013; Baumann and Strass, 2015; Ulbricht, 2021) in-
vestigated a basic question, namely how many exten-
sions can an AF possess under a given semantics. The
results of this line of research have many useful appli-
cations to abstract argumentation, for example they
Trinh, V.-G., Benhamou, B. and Risch, V.
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks.
DOI: 10.5220/0013346400003890
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 17th International Conference on Agents and Artificial Intelligence (ICAART 2025) - Volume 2, pages 745-756
ISBN: 978-989-758-737-5; ISSN: 2184-433X
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
745

can be used to provide lower bounds for the minimal
realizability of certain sets of extensions (Baumann
et al., 2014) and upper bounds for extension compu-
tation algorithms (Baumann and Strass, 2015). There
are also other studies focusing on relationships among
different semantics of an AF under certain graphical
conditions (Dung, 1995; Yun et al., 2017). In this
work, we focus on the graphical analysis of AFs.
Boolean Networks (BNs) are a simple and effi-
cient mathematical formalism that has a long history
of research and has been widely applied to many ar-
eas from science to engineering such as mathematics,
computer science, neural networks, manufacturing,
IoT, and in particular systems biology (Schwab et al.,
2020). A BN is a discrete dynamical system including
n Boolean variables associated with n Boolean func-
tions to express the state update over discrete time fol-
lowing an employed update scheme. Recently, trap
spaces have been proposed (Klarner et al., 2015), and
now have become the central focus in the analysis
and control of BNs (Rozum et al., 2021; Trinh et al.,
2023; Trinh et al., 2024a; Trinh et al., 2024c). A
trap space is a well-structured part of the state space
where the BN’s dynamics cannot escape once en-
tered. If a trap space only contains one state, it is a
fixed point. In contrast to other dynamical concepts
in BNs, trap spaces (also fixed points) are indepen-
dent of the employed update scheme. Very recently,
BNs have been connected to logic programming, and
then used to study the graphical analysis of normal
logic programs (Trinh and Benhamou, 2024; Trinh
et al., 2024b), which are closely related to AFs (Dung,
1995).
Motivated by the aforementioned elements, in this
work, we establish a connection between AFs and
BNs. More specifically, we define a BN encoding for
AFs. We then show that the attack graph of an AF co-
incides with the influence graph of its encoded BN,
and in particular preferred and stable extensions of
this AF one-to-one correspond to minimal trap spaces
and fixed points of the encoded BN, respectively. We
also define a new concept for BNs called complete
trap space (inspired by the concept of complete ex-
tension in AFs), then show that complete trap spaces
(resp. the percolation of the special trap space where
all variables are free) in BNs one-to-one correspond
(resp. corresponds) to complete extensions (resp. the
grounded extension) in AFs. This connection opens
the promising application to the graphical analysis of
AFs. We use it to explore many new results relating
extensions of an AF and (positive or negative) cycles
in its attack graph. In particular, we show new up-
per bounds based on positive feedback vertex sets for
the numbers of stable, preferred, and complete exten-
sions in AFs. Some of these results are quite straight-
forward consequences of existing graphical analysis
results in the BN theory, but there are some results
that rely on new results in the BN theory (including
Theorem 12, Theorem 17, and Theorem 20) that we
claim and formally prove.
In the preparation of the present manuscript, we
have recently noticed that independently from us,
three other groups of researchers have discovered the
connection between AFs and BNs (Dimopoulos et al.,
2024; Heyninck et al., 2024; Azpeitia et al., 2024).
Although sharing some parts of results, our work con-
tains many new results that do not exist in the others.
We list here several notable ones:
• The bijection between the set of complete exten-
sions of an AF and the set of complete trap spaces
of its encoded BN (Theorem 1).
• The equivalence between the grounded extension
of an AF and the percolation of the special trap
space of its encoded BN (Theorem 2).
• A more general characterization of complete trap
spaces in BNs (Theorem 4).
• Importantly, all the graphical analysis results
shown in Section 5.
2 PRELIMINARIES
We use B = {0, 1} as the Boolean domain and the
logical connectives used in this paper are ∧ (conjunc-
tion), ∨ (disjunction), and ¬ (negation).
2.1 Abstract Argumentation
Frameworks
An Abstract Argumentation Framework (AF) is a tu-
ple A = (A, R), where A is a finite set of arguments
1
and R is a binary attack relation on A. An AF A
can be represented as a signed directed graph (called
the attack graph) ag(A ) = (V, E) where V = A and
E = {(ab, ⊖) | (a, b) ∈ R} (⊖ stands for the attack).
Then a
−
(resp. a
+
) denotes the set of predecessors
(resp. successors) of argument a in ag(A ), i.e., the
set of arguments that attack a (resp. attacked by a).
These two concepts can be extended for a subset S
of arguments, i.e., S
−
=
S
a∈S
a
−
and S
+
=
S
a∈S
a
+
.
Conventionally,
/
0
−
=
/
0
+
=
/
0. Given a subset S ⊆ A
(also called an extension). S is conflict-free iff there
are no arguments a and b in S such that a attacks b,
i.e., (a,b) ∈ R. An argument a ∈ A is acceptable w.r.t.
1
The abstract argumentation community mostly focuses
on finite (instead of infinite) AFs.
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
746

S iff ∀b ∈ A: if b attacks a, then b is attacked by some
argument in S. S is admissible iff it is conflict-free and
each argument in S is acceptable w.r.t. S. S is a sta-
ble extension iff S is conflict-free and it attacks every
argument that is not in S, i.e., S
+
= A \ S. S is a pre-
ferred extension iff it is a subset-maximal admissible
set. S is a complete extension iff it is an admissible set
such that for each a acceptable w.r.t. S, a ∈ S. S is a
grounded extension iff it is a subset-minimal complete
extension.
A related, and often interchangeable concept for
extension is labelling introduced by (Caminada and
Gabbay, 2009). A labelling is a mapping λ: A →
{in, out, undec}. The corresponding labelling of an
extension S is γ(S) = {(a, in) | a ∈ S} ∪ {(a,out) |
a ∈ S
+
} ∪ {(a, undec) | a ∈ A \ (S ∪ S
+
)}. We de-
fine in(λ) = {a ∈ A | λ(a) = in}, out(λ) = {a ∈ A |
λ(a) = out}, and undec(λ) = {a ∈ A | λ(a) = undec}.
Then the corresponding extension of λ is in(λ). From
now on, we can use the terms of extension and la-
belling interchangeably. In addition, λ is a complete
labelling iff for each a ∈ A, it holds that: if λ(a) = in
then λ(b) = out for every b ∈ a
−
; if λ(a) = out then
there exists b ∈ a
−
such that λ(b) = in; and if λ(a) =
undec then not every argument b ∈ a
−
has λ(b) = out
and there is no argument b ∈ a
−
has λ(b) = in. A
complete labelling λ is grounded iff in(λ) is subset-
minimal. Given an AF, the grounded extension of this
AF is always unique. A complete labelling λ is pre-
ferred iff in(λ) is subset-maximal. Furthermore, if
in(λ) is subset-maximal (resp. subset-minimal), then
out(λ) is also subset-maximal (resp. subset-minimal).
A preferred labelling λ is stable iff in(λ)∪out(λ) = A.
Complete, grounded, preferred, and stable labellings
correspond to complete, grounded, preferred, and sta-
ble extensions, respectively (Caminada and Gabbay,
2009).
Example 1. Let us consider AF A
1
=
(A
1
, R
1
) with A
1
= {a, b, c} and R
1
=
{(a, b), (a, c), (b, a), (c, b), (c, c)}. The attack
graph of A
1
is given in Figure 1. A
1
has
three conflict-free sets: S
1
=
/
0, S
2
= {a}, and
S
3
= {b}. We have three corresponding la-
bellings: γ(S
1
) = {(a, undec), (b, undec), (c, undec)},
γ(S
2
) = {(a, in), (b, out), (c, out)}, and γ(S
3
) =
{(a, out), (b, in), (c, undec)}. S
1
and S
2
are admissi-
ble sets, which are also complete extensions of A
1
.
S
1
is the unique grounded extension of A
1
. S
2
is
a preferred (also stable) extension of A
1
. We also
have that γ(S
1
) and γ(S
2
) are complete labellings,
γ(S
1
) is the unique grounded labelling, and γ(S
2
) is a
preferred (also stable) labelling of A
1
.
a
b
c
⊖
⊖
⊖
⊖ ⊖
Figure 1: Attack graph of A
1
shown in Example 1 and in-
fluence graph of f
1
shown in Example 2.
2.2 Boolean Networks
A Boolean Network (BN) f is a finite set of Boolean
functions on a set of Boolean variables denoted by
var
f
. Each variable v is associated with a Boolean
function f
v
: B
|var
f
|
→ B. f
v
is called constant if it
is always either 0 or 1 regardless of the values of its
arguments. A state s of f is a Boolean vector s ∈
B
|var
f
|
. s can be seen as a mapping s : var
f
→ B. We
write s
v
to denote the value of variable v in s. For
convenience, we write a state simply as a string of
values of variables in this state (e.g., 0110 instead of
(0, 1, 1, 0)).
Let x be a state of f . We use x[v ← a] to denote
the state y so that y
v
= a and y
u
= x
u
, ∀u ∈ var
f
, u ̸= v
where a ∈ B. The Influence Graph (IG) of f (denoted
by ig( f )) is a signed directed graph (V, E) on the set
of signs {⊕, ⊖} where V = var
f
, (uv, ⊕) ∈ E (i.e., u
positively affects the value of f
v
) iff there is a state x
such that f
v
(x[u ← 0]) < f
v
(x[u ← 1]), and (uv, ⊖) ∈ E
(i.e., u negatively affects the value of f
v
) iff there is a
state x such that f
v
(x[u ← 0]) > f
v
(x[u ← 1]). Let v
−
(resp. v
+
) denote the set of predecessors (resp. suc-
cessors) of v in ig( f ). Then |v
−
| (resp. |v
+
|) is called
the in-degree (resp. out-degree) of v. The minimum
in-degree of ig( f ) is defined as the smallest in-degree
of all vertices v in ig( f ). Clearly, f contains no con-
stant function iff the minimum in-degree of ig( f ) is at
least one. A cycle (possibly a self loop) of a signed di-
rected graph is positive (resp. negative) if its number
of arcs is even (resp. odd). A positive (resp. negative)
feedback vertex set is a set of vertices that intersect all
positive (resp. negative) cycles.
At each time step t, variable v can update its
state to s
′
v
= f
v
(s), where s (resp. s
′
) is the state of
f at time t (resp. t + 1). An update scheme of a
BN refers to how variables update their states over
(discrete) time (Schwab et al., 2020). Various up-
date schemes exist, but the primary types are syn-
chronous, where all variables update simultaneously,
and fully asynchronous, where a single variable is
non-deterministically chosen for updating. By adher-
ing to the employed update scheme, the BN transi-
tions from one state to another, which may or may not
be the same. This transition is referred to as the state
transition. Then the dynamics of the BN is captured
by a directed graph referred to as the State Transition
Graph (STG). We use sstg( f ) (resp. astg( f )) to de-
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks
747

note the STG of f under the synchronous (resp. fully
asynchronous) update scheme.
A non-empty set of states is a trap set if it has
no out-going arcs on the STG of f . An attractor is a
subset-minimal trap set. An attractor of size 1 (resp. at
least 2) is called a fixed point (resp. cyclic attractor).
A sub-space m of a BN f is a mapping m: var
f
→ B
⋆
where B
⋆
= B ∪ {⋆} denoting the three-valued do-
main. A variable v ∈ var
f
is called fixed (resp. free)
in m iff m(v) ̸= ⋆ (resp. m(v) = ⋆). A sub-space m
represents a set of states denoted by S [m] such that
S [m] = {s ∈ B
|var
f
|
|s
v
= m(v), ∀v ∈ var
f
, m(v) ̸= ⋆}.
For example, m = {v
1
= ⋆, v
2
= 1, v
3
= 1} and S [m] =
{011, 111}. If a sub-space is also a trap set, it is
a trap space. Unlike trap sets and attractors, trap
spaces of a BN are independent of the employed up-
date scheme (Klarner et al., 2015). In particular, a
fixed point of f is a special trap space where no vari-
able is mapped to ⋆. A trap space m is minimal iff
there is no trap space m
′
such that S[m
′
] ⊂ S [m]. Since
an attractor is a subset-minimal trap set, a minimal
trap space contains at least one attractor of the BN
regardless of the employed update scheme.
Example 2. Let us consider BN f
1
with var
f
1
=
{a, b, c}, f
1
a
= ¬b, f
1
b
= ¬a ∧ ¬c, and f
1
c
= ¬a ∧ ¬c.
The IG of f
1
is given in Figure 1. Figures 2(a)
and 2(b) respectively show the synchronous and asyn-
chronous STGs of f
1
where self arcs are omitted for
simplicity. sstg( f
1
) has one fixed point ({100}) and
one cyclic attractor ({000, 111}). astg( f
1
) has only
one fixed point ({100}). f
1
has three trap spaces
(same in the both STGs): m
1
= {a = ⋆, b = ⋆, c = ⋆},
m
2
= {a = 1, b = 0, c = 0}, m
3
= {a = 1, b = 0, c = ⋆}.
Then m
2
is a minimal trap space of f
1
.
000 110 010
111 011 001
101 100
(a) .
000 110 010
111 011 001
101 100
(b) .
Figure 2: (a) sstg( f
1
) and (b) astg( f
1
). f
1
is given in Ex-
ample 2.
3 RELATED WORK
3.1 Connections with Other Theories
AFs are closely connected to logic programming,
one of non-monotonic reasoning frameworks, start-
ing from the early studies (Pollock, 1991b; Pollock,
1991a; Dung, 1995). Subsequent studies of this direc-
tion (Caminada and Gabbay, 2009; Caminada et al.,
2015) showed more clearly the equivalence between
extensions in AFs and models in logic programs such
as stable extensions vs. stable models, complete ex-
tensions vs. stable partial models, and preferred ex-
tensions vs. regular models. Key to prove the equiv-
alence is the use of labellings (Caminada and Gab-
bay, 2009). There are also some studies trying to en-
code preferred extensions as stable models of logic
programs (Nieves et al., 2008). Furthermore, AFs
were also connected to default theories (Nouioua and
Risch, 2012), thus it showed that any admissible (or
preferred) set of arguments of an AF can be directly
computed from the ι-answer sets of its equivalent
logic program.
Because of the intuitive formalization using di-
rected graphs, AFs were naturally connected to
graph theory (Dimopoulos and Torres, 1996). Sev-
eral equivalence results have been obtained, not
only pointing out computational tractable classes of
AFs under certain graph-theoretic constraints (Dunne,
2007) but also contributing to the analysis of
AFs (Gaspers and Li, 2019). Recently, AFs have been
connected to lattices (Elaroussi et al., 2023) (in terms
of preferred extensions) and formal concept analy-
sis (Obiedkov and Sertkaya, 2023) (in terms of stable
extensions).
3.2 Graphical Analysis
In his 1995 seminal paper, Dung also provided some
essential results regarding the graphical analysis of
AFs (Dung, 1995). For example, he showed that
an AF without cycles in its attack graph has exactly
one complete extension that is also preferred and sta-
ble. He also showed that if the attack graph has no
negative cycles, then the stable and preferred exten-
sions of the AF coincide, leading to it has at least
one stable extension. Subsequent studies (Baumann
and Strass, 2013; Ulbricht, 2021; Baumann and Ul-
bricht, 2021) dived deeply into the question of how
many extensions can an AF possess under a given se-
mantics. The work by (Baumann and Strass, 2013)
presented a first analytical and empirical study of the
maximal and average numbers of stable extensions,
in particular showing that for any AF of n arguments,
the number of stable extensions is at most 3
n
3
. This
number was latter shown to be an upper bound for the
number of preferred extensions (Dunne et al., 2015).
Recently, the work by (Ulbricht, 2021) has answered
a reasonable conjecture claimed in (Baumann and
Strass, 2015) on the maximal number of complete ex-
tensions. More specifically, it shows that the number
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
748

of complete extensions of any AF of n arguments is at
most 3
n
2
. Finally, a branch of this research direction
is to investigate graphical properties of special types
of AFs such as symmetric AFs (Coste-Marquis et al.,
2005).
4 AF-BN CONNECTION
4.1 BN Encoding
We first define a BN encoding of AFs as follows.
Definition 1. Let A = (A, R) be an AF. Its encoded
BN f is: var
f
= A, f
a
=
V
b∈a
−
¬b, ∀a ∈ A. If a
−
=
/
0,
then f
a
= 1.
A BN f is called negative AND-NOT iff every its
update function is only a conjunction of negative lit-
erals (Richard and Ruet, 2013). Clearly, a negative
AND-NOT BN is uniquely determined by its influ-
ence graph. In particular, the encoded BN of an AF is
a negative AND-NOT BN.
A straightforward consequence from the encoding
is:
Proposition 1. Let A = (A, R) be an AF and f be its
encoded BN. Then ag(A) = ig( f ).
Indeed, the example BN f
1
(see Example 2) is the
encoded BN of the example AF A
1
(see Example 1).
The influence graph of f
1
and the attack graph of A
1
are the same (see Figure 1). ig( f
1
) has one positive
cycle (a
⊖
−→ b
⊖
−→ a) and two negative cycles (c
⊖
−→ c
and a
⊖
−→ c
⊖
−→ b
⊖
−→ a). By considering in as 1, out
as 0, and undec as ⋆, we can obtain the equivalence
between labellings in an AF and sub-spaces in a BN.
From now on, we can use these terms interchange-
ably. As such, trap space m
1
(resp. m
2
) of f
1
is equiv-
alent to complete labelling γ(S
1
) (resp. γ(S
2
)) of A
1
.
Trap space m
3
of f
1
does not correspond to any com-
plete labelling of A
1
. However, we can see the equiv-
alence between minimal trap spaces of f
1
(i.e., m
2
)
and preferred labllings of A
1
(i.e., γ(S
2
)). In addition,
m
1
is equivalent to the grounded labelling γ(S
1
).
4.2 Complete Extensions
First, we define the order ≤
s
on B
⋆
by 0 <
s
⋆, 1 <
s
⋆,
and ≤
s
contains no other relation. Then for two sub-
spaces m
1
and m
2
, we have m
1
≤
s
m
2
iff m
1
(a) ≤
s
m
2
(a), ∀a ∈ var
f
. It is also similar for labellings. In
addition, m
1
≤
s
m
2
iff S [m
1
] ⊆ S [m
2
], and m
1
<
s
m
2
iff m
1
≤
s
m
2
and m
1
̸= m
2
. It follows that ≤
s
-minimal
trap spaces are exactly minimal trap spaces and pre-
ferred labellings are exactly ≤
s
-minimal complete la-
bellings. Second, we define the truth order ≤
t
on B
⋆
by 0 <
t
⋆ <
t
1. Let e be a propositional formula on
var
f
. Then the evaluation of e under a sub-space m
(denoted by m(e)) is defined recursively as follows:
m(e) =









m(a) if e = a, a ∈ var
f
¬m(e
1
) if e = ¬e
1
min
≤
t
(m(e
1
), m(e
2
)) if e = e
1
∧ e
2
max
≤
t
(m(e
1
), m(e
2
)) if e = e
1
∨ e
2
where ¬1 = 0, ¬0 = 1, ¬⋆ = ⋆, and min
≤
t
(resp.
max
≤
t
) is the function to get the minimum (resp. max-
imum) value of two values w.r.t. the order ≤
t
. Note
that if s is a state (i.e., a special sub-space where no
variable is mapped to ⋆), then s(e) = e(s) as s is also
a vector of Boolean values. We have the following
property for trap spaces.
Definition 2. Given a BN f . We define T ( f ) as the
set of all sub-spaces m such that m( f
a
) ≤
s
m(a) for
every a ∈ var
f
.
Proposition 2. Let f be a BN. Then T ( f ) is exactly
the set of all trap spaces of f .
Proof. Let m be a sub-space of f . Let s be a state in
S [m]. It follows that s ≤
s
m. Let s
′
be a successor
state of s following the employed update scheme of
f . For any variable a ∈ var
f
, if a is updated, then
s
′
a
= f
a
(s) = s( f
a
), and s
′
a
= s
a
otherwise. We also
have that s( f
a
) ≤
s
m( f
a
), ∀a ∈ var
f
because s ≤
s
m.
Then m ∈ T ( f ) iff m( f
a
) ≤
s
m(a) for every a ∈ var
f
by definition iff s
′
a
≤
s
m(a) for every a ∈ var
f
iff s
′
∈
S [m] (regardless of the employed update scheme) iff
m is a trap space of f .
By Proposition 2, we can use T ( f ) as the set of
all trap spaces of f . Next, inspired by the concept of
complete extension in AFs, we propose a new concept
called complete trap space for BNs (see Definition 3).
Definition 3. Given a BN f . A sub-space m is called a
comple trap space iff m( f
a
) = m(a) for every a ∈ var
f
.
We denote
b
T ( f ) be the set of all complete trap spaces
of f .
Considering the example BN f
1
(given in Ex-
ample 2), we have T ( f
1
) = {m
1
, m
2
, m
3
}, whereas
b
T ( f
1
) = {m
1
, m
2
}. Of course, we can see that
b
T ( f ) ⊆
T ( f ) for any BN f by definition. We then prove a
deeper relationship between trap spaces in
b
T ( f ) and
trap spaces in T ( f ).
Proposition 3. Let f be a BN. For every m ∈ T ( f ),
there is a trap space
b
m ∈
b
T ( f ) such that
b
m ≤
s
m.
Proof. Let m
j
be an arbitrary trap space in T ( f ).
We construct a sub-space m
j+1
as m
j+1
(a) =
m
j
( f
a
), ∀a ∈ var
f
.
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks
749

We prove that m
j+1
is also a trap space of f .
By construction, it is a sub-space. In addition,
m
j+1
(a) ≤
s
m
j
(a), ∀a ∈ var
f
because m
j
is a trap
space, thus m
j+1
≤
s
m
j
. Let s be an arbitrary state
in S [m
j+1
]. Of course, it is also in S [m
j
] because
m
j+1
≤
s
m
j
. Let s
′
be the next state of s on sstg( f )
(the synchronous STG of f ), i.e., s
′
a
= s( f
a
), ∀a ∈
var
f
. Consider variable a ∈ var
f
. Since s ∈ S[m
j
], we
have that s( f
a
) ≤
s
m
j
( f
a
), leading to s
′
a
≤
s
m
j+1
(a).
Hence, s
′
∈ S [m
j+1
], i.e., S [m
j+1
] is a trap set of
sstg( f ). It follows that m
j+1
is a trap space.
Assume that m is a trap space in T ( f ). We start
with m
j
= m and repeat the above process by increas-
ing j, and finally reach the case m
j+1
= m
j
because
S [m] is finite. By construction, m
j
(a) = m
j
( f
a
), ∀a ∈
var
f
(thus m
j
∈
b
T ( f )) and m
j
≤
s
m. By setting
b
m = m
j
, we can conclude the proof.
We then show that
b
T ( f ) is exactly the set of all
complete labellings of the AF A.
Theorem 1. Let A = (A, R) be an AF and f be its
encoded BN. The set of complete labellings of A co-
incides with the set
b
T ( f ).
Proof. By construction, var
f
= A. Let λ be a labelling
of A . It can be considered as a sub-space of f . Con-
sider an argument a ∈ A. Recall that f
a
=
V
b∈a
−
¬b.
We have by definition that λ(b) = out for every b ∈ a
−
iff λ( f
a
) = 1. There is b ∈ a
−
such that λ(b) = in iff
λ( f
a
) = 0. Not every argument b ∈ a
−
has λ(b) = out
and there is no argument b ∈ a
−
has λ(b) = in iff
λ( f
a
) can be neither 0 nor 1 iff λ( f
a
) = ⋆. This im-
plies that λ is a complete labelling of A iff λ(a) =
λ( f
a
), ∀a ∈ A iff λ is a trap space in
b
T ( f ).
4.3 Grounded Extensions
We here show that the grounded extension of an AF
corresponds to a special complete trap space of its en-
coded BN (Theorem 2).
Definition 4 ((Trinh et al., 2024c)). Given a sub-
space m, the single-step percolation operator P pro-
duces a sub-space (denoted by P (m)) with fixed vari-
ables given by those of m together with the free vari-
ables of m whose update functions are invariant on m.
Formally, P (m)(v) = m(v) if m(v) ̸= ⋆, P (m)(v) =
b ∈ B if m(v) = ⋆ and f
v
(x) = b, ∀x ∈ S [m], and
P (m)(v) = ⋆ otherwise. The percolation operator P
ω
is obtained by repeated application of the single-step
percolation operator P until a fixpoint, which always
exists and can be achieved after up to |var
f
| applica-
tion times because var
f
is finite. We call P
ω
(m) the
percolation of m.
Proposition 4. Given a BN f . If m is a trap space of
f , then P
ω
(m) is a complete trap space of f .
Proof. It is easy to see that if m is a trap space, then
P (m) is unique and also a trap space. Hence, P
ω
(m)
is unique and also a trap space in which Boolean func-
tions of free variables cannot be simplified further un-
der P
ω
(m). Of course, P
ω
(m)( f
v
) = P
ω
(m)(v) for
every fixed variable v in P
ω
(m). For every free vari-
able v in P
ω
(m), P
ω
(m)( f
v
) = ⋆ = P
ω
(m)(v). By
definition, P
ω
(m) is a complete trap space.
Theorem 2. Let A be an AF and f be its encoded BN.
The grounded labelling of A equals to the percolation
of sub-space ε where ε(v) = ⋆, ∀v ∈ var
f
.
Proof. Of course, ε is a trap space of f . By Proposi-
tion 4, P
ω
(ε) is a complete trap space of f .
For any trap spaces m
1
and m
2
of f , P (m
1
) ≤
s
P (m
2
) if m
1
≤
s
m
2
. It follows that P
ω
(m
1
) ≤
s
P
ω
(m
2
) if m
1
≤
s
m
2
. Since m ≤
s
ε for every trap
space m, P
ω
(m) ≤
s
P
ω
(ε). Since P
ω
(m) is a com-
plete trap space, P
ω
(ε) is the (unique) ≤
s
-maximal
complete trap space of f .
By definition, the grounded labelling of A is the
unique subset-minimal complete labelling of A. We
have that ≤
s
-maximal equals to subset-minimal. By
Theorem 1, the grounded labelling of A equals to
P
ω
(ε).
4.4 Preferred and Stable Extensions
First, we show that preferred extensions of an AF A
one-to-one correspond to minimal trap spaces of its
encoded BN f .
Theorem 3. Let A = (A, R) be an AF and f be its
encoded BN. The set of preferred labellings of A co-
incides with the set of minimal trap spaces of f .
Proof. We first show that a sub-space m is a ≤
s
-
minimal trap space w.r.t. T ( f ) iff it is a ≤
s
-minimal
trap space w.r.t.
b
T ( f ). The “⇒” direction is trivial,
since
b
T ( f ) ⊆ T ( f ). For the “⇐” direction, assume
that m is not ≤
s
-minimal w.r.t. T ( f ). Then there is a
trap space m
′
in T ( f ) such that m
′
<
s
m. By Propo-
sition 3, there is a trap space
b
m ∈
b
T ( f ) such that
b
m ≤
s
m
′
. Then
b
m <
s
m, which is a contradiction be-
cause m is ≤
s
-minimal w.r.t.
b
T ( f ). Hence, m is also a
≤
s
-minimal trap space w.r.t. T ( f ).
Now, we have that the set of minimal trap spaces
of f coincides with the set of ≤
s
-minimal trap spaces
of
b
T ( f ). By Theorem 1, the set of complete labellings
of A coincides with
b
T ( f ). Recall that a preferred la-
belling is a ≤
s
-minimal complete labelling. Hence,
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
750

the set of preferred labellings of A coincides with the
set of minimal trap spaces of f .
Actually, Theorem 3 has been also claimed and
proved in (Heyninck et al., 2024; Azpeitia et al.,
2024) (but not in (Dimopoulos et al., 2024)) using a
different way of proof. Next, we show the follow-
ing corollary. This implies that stable extensions of A
one-to-one correspond to fixed points of f .
Corollary 1. Let A = (A, R) be an AF and f be its en-
coded BN. The set of stable labellings of A coincides
with the set of fixed points of f .
Proof. λ is a stable labelling of A iff it is a preferred
labelling and λ(a) ̸= undec, ∀a ∈ A iff λ is a minimal
trap space of f by Theorem 3 and λ(a) ̸= ⋆, ∀a ∈ var
f
iff λ is a fixed point of f .
4.5 Characterization of Complete Trap
Spaces
To end this section, we show a more general char-
acterization of complete trap spaces in BNs (Theo-
rem 4). Let [S] denote the smallest sub-space that in-
duces a set of states S (i.e., S ⊆ S [[S]]). Let next(S)
denote the set of next states in the synchronous STG
of states in S.
Theorem 4. Given a BN f and a sub-space m of f .
m is a complete trap space of f iff m = [next(S [m])].
Proof. “⇒” Assume that m is a complete trap space.
For every v ∈ var
f
such that m(v) ̸= ⋆, we have
s
v
= m(v), ∀s ∈ next(S[m]). For every v ∈ var
f
such
that m(v) = ⋆, f
v
cannot be simplified further under
m, thus there always exists state s (resp. s
′
) in S [m]
such that f
v
(s) = 0 (resp. f
v
(s
′
) = 1). It follows that
[next(S[m])](v) = ⋆. Hence, m = [next(S [m])].
“⇐” Assume that m = [next(S [m])]. Then
next(S[m]) ⊆ S [m] by definition, implying that S [m]
is a trap set in sstg( f ), thus m is a trap space of
f . Suppose that m is not complete. It follows that
P
ω
(m) <
s
m (see the proof of Theorem 2), since
P
ω
(m) is a complete trap space by Proposition 4.
Then there is a variable v ∈ var
f
such that m(v) = ⋆,
but P (m)(v) ̸= ⋆. This implies that ∀s ∈ next(S[m]),
s
v
= P (m)(v), thus m ̸= [next(S[m])], which is a con-
tradiction. Hence, m is a complete trap space.
The general characterization shown in Theorem 4
relies on next states in the synchronous STG. It can
be applicable for any BN. In contrast, the character-
ization shown in (Dimopoulos et al., 2024) relies on
two-state attractors in the the synchronous STG and
is applicable for only negative AND-NOT BNs.
Example 3. Consider the BN f
1
given in Exam-
ple 2. f
1
is the encoded BN of the AF A
1
given in
Example 1. f
1
has three trap spaces: m
1
= {a =
⋆, b = ⋆, c = ⋆}, m
2
= {a = 1, b = 0, c = 0}, m
3
=
{a = 1, b = 0, c = ⋆}. m
1
and m
2
are complete. We
have [next(S[m
1
])] = [{000, 011, 100, 111}] = {a =
⋆, b = ⋆, c = ⋆} = m
1
and [next(S [m
2
])] = [{100}] =
{a = 1, b = 0, c = 0} = m
2
. m
3
is not complete and
[next(S[m
3
])] = [{100}] = {a = 1,b = 0, c = 0} ̸= m
3
.
5 GRAPHICAL ANALYSIS
RESULTS
The graphical analysis of BNs has a long history of re-
search since BNs were originated (Kauffman, 1969).
Nowadays, this line of research is still active with
many prominent and deep results obtained, for exam-
ple, the relationships between fixed points or attrac-
tors and positive or negative cycles in the influence
graph, the upper bounds for numbers of fixed points
or attractors based on feedback vertex sets in the influ-
ence graph. See (Paulev
´
e and Richard, 2012; Richard,
2019) for more detailed reviews. The established con-
nection between AFs and BNs opens the door to ex-
ploit these results for the graphical analysis of AFs,
an interesting and crucial line of research on abstract
argumentation. An advantage of the above approach
is that we now can focus only on the dynamical prop-
erties in BNs when studying extensions in AFs.
5.1 Negative Cycles
First, we provide new proofs for the two known re-
sults presented in (Dung, 1995).
Theorem 5 (Theorem 33(1) of (Dung, 1995)). Given
an AF A. If ag(A ) has no negative cycle, then all
preferred extensions of A are stable.
New proof. Let f be the encoded BN of A. By Propo-
sition 1, ig( f ) has no negative cycle. By Theorem
1 of (Richard, 2010), astg( f ) has no cyclic attractor.
Each minimal trap space of f contains at least one
attractor of astg( f ) (Klarner et al., 2015). In addi-
tion, if a minimal trap space contains a fixed point,
then it is also a fixed point because of the minimality.
Hence, all minimal trap spaces of f are fixed points.
By Theorem 3 and Corollary 1, we can conclude that
all preferred extensions of A are stable.
Corollary 2. Given an AF A . If ag(A) has no nega-
tive cycle, then A has at least one stable extension.
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks
751

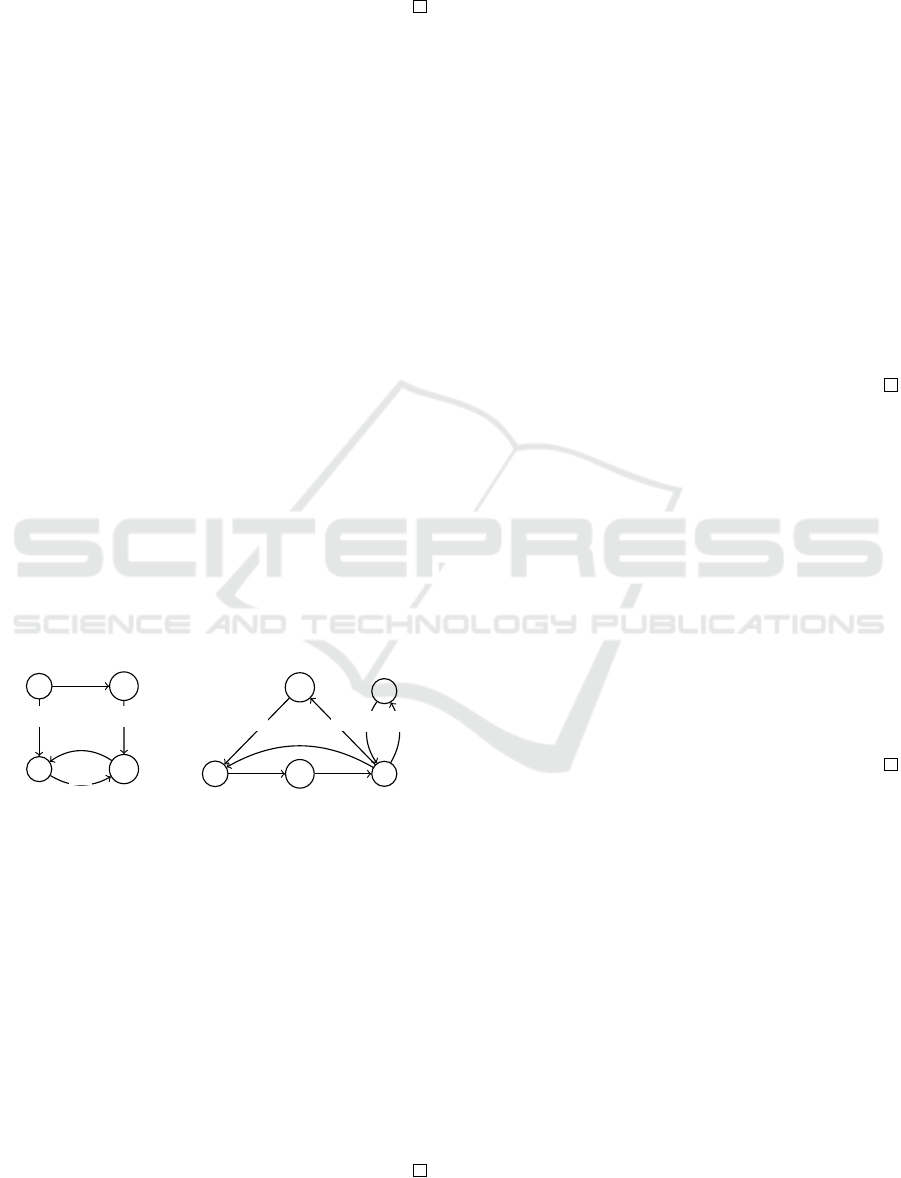
Proof. By Theorem 5, all preferred extensions of A
are stable. Since A has at least one preferred exten-
sion (Dung, 1995), it has at least one stable exten-
sion.
Next, we show a new result on stable extensions
(Theorem 7).
Definition 5 ((Richard and Ruet, 2013)). Given a
signed directed graph G without positive arcs and
vertices u, v of G (not necessarily distinct). A ver-
tex w ̸= u, v is said to be a subdivision of (u, v) when
1) (uw, ⊖) and (wv, ⊖) are arcs of G; 2) (uv, ⊖) is not
an arc of G; 3) the in-degree and out-degree of w both
equal 1.
Definition 6 ((Richard and Ruet, 2013)). Given a
signed directed graph G without positive arcs, a cycle
C of G and vertices u, v
1
, v
2
of G. (u, v
1
, v
2
) is called
a killing triple of C when 1) v
1
and v
2
are distinct ver-
tices of C; 2) (u, v
1
) has a subdivision in G, but no
subdivision of (u, v
1
) belongs to C; 3) (uv
2
, ⊖) is an
arc of G that is not in C. A killing triple (u, v
1
, v
2
) of C
is internal when u is a vertex in C, external otherwise.
Example 4. Consider two signed directed graphs
without positive arcs: G
1
and G
2
(see Figures 3(a)
and 3(b), respectively). In G
1
, (a, d, c) is an external
killing triple of positive cycle c
⊖
−→ d
⊖
−→ c with b is
a subdivision of (a, d). In G
2
, (c, c, a) is an internal
killing triple of positive cycle a
⊖
−→ b
⊖
−→ c
⊖
−→ d
⊖
−→ a
with e is a subdivision of (c, c). Positive cycle c
⊖
−→
e
⊖
−→ c has no killing triple in G
2
.
a
b
c
d
⊖
⊖
⊖
⊖
⊖
(a) .
a
b
c
d
e
⊖⊖
⊖ ⊖
⊖
⊖
⊖
(b) .
Figure 3: (a) G
1
and (b) G
2
. These graphs are considered in
Example 4.
Theorem 6 ((Richard and Ruet, 2013)). Given a neg-
ative AND-NOT BN f . If every negative cycle of ig( f )
has an internal killing triple, then f has at least one
fixed point.
Theorem 7. Given an AF A. If every negative cycle
of ag(A) has an internal killing triple, then A has at
least one stable extension.
Proof. Let f be the encoded BN of A. By Proposi-
tion 1, every negative cycle of ig( f ) has an internal
killing triple. By Theorem 6, f has at least one fixed
point. By Corollary 1, A has at least one stable exten-
sion.
Indeed, ag(A ) has no negative cycle implies that
every negative cycle of ag(A) has an internal killing
triple holds true. Hence, Theorem 7 is stronger than
Corollary 2.
5.2 Positive Cycles
We first show that the presence of positive cycles in
the attack graph is the necessary condition for the ex-
istence of multiple stable or preferred extensions.
Theorem 8 ((Aracena, 2008)). Let f be a BN. If ig( f )
has no positive cycle, then f has at most one fixed
point.
Theorem 9. Given an AF A . If ag(A) has no positive
cycle, then A has at most one stable extension.
Proof. Let f be the encoded BN of A. By Proposi-
tion 1, ig( f ) has no positive cycle. By Theorem 8, f
has at most one fixed point. By Corollary 1, A has at
most one stable extension.
Theorem 10 ((Richard and Comet, 2007)). Let f be
a BN. If ig( f ) has no positive cycle, then astg( f ) has
a unique attractor.
Theorem 11. Given an AF A . If ag(A ) has no posi-
tive cycle, then A has a unique preferred extension.
Proof. Let f be the encoded BN of A . By Propo-
sition 1, ig( f ) has no positive cycle. By Theo-
rem 10, astg( f ) has a unique attractor. Each mini-
mal trap space of f contains at least one attractor of
astg( f ) (Klarner et al., 2015) and S [m
1
] ∩ S [m
2
] =
/
0
for any two distinct minimal trap spaces m
1
, m
2
(Trinh
et al., 2023). It follows that f has at most one mini-
mal trap space. Since f has at least one minimal trap
space, f has a unique minimal trap space. By Theo-
rem 3, A has a unique preferred extension.
Surprisingly, this condition also holds true for
complete extensions (Theorem 13). Note that the
proof for this result relies on Theorem 12 that is new
in the BN theory.
Lemma 1. Let f be the negative AND-NOT BN. As-
sume that ig( f ) has the minimum in-degree of at least
one. If ig( f ) has no positive cycle, then f has a unique
complete trap space.
Proof. Since ig( f ) has the minimum in-degree of at
least one, f has no constant function. Then the sub-
space ε where all variables are free is simply a com-
plete trap space of f .
Assume that f has a complete trap space m ̸= ε.
Then there exists a variable v
0
such that m(v
0
) ̸= ⋆.
If m(v
0
) = 1, then m( f
v
0
) = 1 because m is com-
plete, leading to m(v) = 0 for every v ∈ v
−
0
(as f
v
0
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
752

is a conjunction of negative literals), thus there is
v
1
∈ v
−
0
such that m(v
1
) = 0 because ig( f ) has the
minimum in-degree of at least one. If m(v
0
) = 0,
then m( f
v
0
) = 0 because m is complete, leading to
there is v
1
∈ v
−
0
such that m(v
1
) = 1. Repeating
this reasoning, we have an infinite descending chain
v
0
⊖
←− v
1
⊖
←− v
2
. . . such that m(v
i
) ̸= ⋆, ∀i ≥ 0 and
m(v
i+1
) = ¬m(v
i
). Since var
f
is finite, there ex-
ist two integer numbers j and k ( j, k ≥ 0) such that
v
j
= v
j+k
in the infinite descending chain, i.e., C =
v
j
⊖
←− v
j+1
⊖
←− . . .
⊖
←− v
j+k−1
⊖
←− v
j
is a cycle of ig( f ).
We have that m(v
j
) = m(v
j+2
) = . . ., thus k is even.
Hence, C is a positive cycle, which is a contradiction.
Now we can conclude that f has a unique com-
plete trap space.
Theorem 12. Given a negative AND-NOT BN f . If
ig( f ) has no positive cycle, then f has a unique com-
plete trap space.
Proof. By percolating constant functions of f (sim-
ilar to the percolation on trap spaces shown in Def-
inition 4), we get either a non-empty BN f
′
with-
out constant functions or an empty BN. In the lat-
ter case, we have that f has a unique complete trap
space. In the former case, we have that f
′
is a neg-
ative AND-NOT BN and has no constant function,
equivalently ig( f
′
) has the minimum in-degree of at
least one. ig( f ) has no positive cycle, thus ig( f
′
) has
no positive cycle because ig( f
′
) is clearly a sub-graph
of ig( f ). By Lemma 1, f
′
has a unique complete trap
space. Clearly, there is a bijection between the set of
complete trap spaces of f and that of f
′
. Hence, f has
a unique complete trap space.
Theorem 13. Given an AF A . If ag(A ) has no posi-
tive cycle, then A has a unique complete extension.
Proof. It straightforwardly follows from Proposi-
tion 1, Theorem 1, and Theorem 12.
Finally, we show a stronger result of Theorem 9.
Theorem 14 ((Richard and Ruet, 2013)). Given a
negative AND-NOT BN f . If every positive cycle of
ig( f ) has a killing triple, then f has at most one fixed
point.
Theorem 15. Given an AF A . If every positive cycle
of ag(A ) has a killing triple, then A has at most one
stable extension.
Proof. Let f be the encoded BN of A. By Proposi-
tion 1, every positive cycle of ig( f ) has a killing triple.
By Theorem 14, f has at most one fixed point. By
Corollary 1, A has at most one stable extension.
5.3 Upper Bounds
Hereafter, we show three new upper bounds for the
numbers of preferred, stable, and complete extensions
of an AF, respectively. To the best of our knowledge,
they are the first results relating the numbers of pre-
ferred, stable, and complete extensions with positive
feedback vertex sets of the attack graph.
Theorem 16. Given an AF A. Let U be a subset of
vertices that intersects every positive cycle of ag(A).
Then A has at most 2
|U|
preferred extensions.
Proof. Let f be the encoded BN of A. By Proposi-
tion 1, U intersects every positive cycle of ig( f ). By
Corollary 2 of (Richard, 2009), astg( f ) has at most
2
|U|
attractors. It follows that f has at most 2
|U|
mini-
mal trap spaces. By Theorem 3, we can conclude that
2
|U|
is an upper bound for the number of preferred
extensions of A.
Corollary 3. Given an AF A . Let U be a subset of
vertices that intersects every positive cycle of ag(A).
Then A has at most 2
|U|
stable extensions.
Proof. By Theorem 16, A has at most 2
|U|
preferred
extensions. A stable extension is also a preferred ex-
tension, thus A has at most 2
|U|
stable extensions.
Theorem 17. Given a negative AND-NOT BN f . Let
U be a subset of vertices that intersects every positive
cycle of ig( f ). Then f has at most 3
|U|
complete trap
spaces.
Proof. For each assignement m: U 7→ B
⋆
, we build
the transformed BN f
m
of f as follows. For all a ∈ U,
if m(a) ̸= ⋆, then f
m
a
= m(a); otherwise, f
m
a
= ¬a.
For all a ∈ var
f
\U, f
m
a
= f
a
. Indeed, ig( f
m
) has no
positive cycle, since U intersects all positive cycles
of ig( f ), and the construction removes all predeces-
sors of vertices in U on ig( f ) and only adds to ig( f
m
)
a new negative cycle a
⊖
−→ a in the case m(a) = ⋆.
Clearly, f
m
is a negative AND-NOT BN. By Theo-
rem 12, f
m
has a unique complete trap space.
Note that the complete trap spaces of f agreeing
with m are complete trap spaces of f
m
. There are 3
|U|
possible assignments w.r.t. U. Hence, f has at most
3
|U|
complete trap spaces.
Theorem 18. Given an AF A. Let U be a subset of
vertices that intersects every positive cycle of ag(A).
Then A has at most 3
|U|
complete extensions.
Proof. It straightforwardly follows from Proposi-
tion 1, Theorem 1, and Theorem 17.
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks
753

Finally, we show a tighter upper bound for the
number of stable extensions of an AF (Theorem 21) as
if a subset of vertices intersects every positive cycle,
it also intersects every positive cycle without a killing
triple of the attack graph.
In an AND-NOT BN, every update function is
only a conjunction of literals. Similar to negative
AND-NOT BNs, an AND-NOT BN is uniquely de-
termined by its influence graph.
Definition 7 ((Richard and Ruet, 2013)). Given a
signed directed graph G, a cycle C of G, and vertices
u, v
1
, v
2
of G. (u, v
1
, v
2
) is said to be a delocalizing
triple of C when 1) v
1
, v
2
are distinct vertices of C; 2)
(uv
1
, ⊕) and (uv
2
, ⊖) are arcs of G that are not in C.
Theorem 19 ((Veliz-Cuba et al., 2012)). Let f be an
AND-NOT BN. Assume that U
0
is a subset of vertices
that intersects every positive cycle without a delocal-
izing triple. Then f has at most 2
|U
0
|
fixed points.
Theorem 20. Given a negative AND-NOT BN f . Let
U
0
be a subset of vertices that intersects every positive
cycle without a killing triple of ig( f ). Then f has at
most 2
|U
0
|
fixed points.
Proof. We build from f a new BN f
′
as follows. For
every positive cycle C in ig( f ) having a killing triple
(u, v
1
, v
2
), let w be a subdivision of (u, v
1
). Then we
remove w from f and replace w by ¬u in f
v
1
. We
always can do this because the in-degree and the out-
degree of w both equal 1. Finally, we obtain f
′
that is
an AND-NOT BN, but may not be a negative AND-
NOT BN.
C can still be a cycle in ig( f
′
) or it becomes a new
cycle with one vertex fewer in ig( f
′
). In any case, C
still contains to a positive cycle C
′
in ig( f
′
). We have
two cases for each C
′
as follows.
Case 1: u ̸= v
1
. We have that (uv
2
, ⊖) is an arc of
ig( f
′
) but it does not belong to C
′
. (uv
1
, ⊕) is an arc of
ig( f
′
). Since (uv
1
, ⊖) is not an arc of ig( f ), (uv
1
, ⊕)
does not belong to C
′
. By definition, (u, v
1
, v
2
) is a
delocalizing triple of C
′
.
Case 2: u = v
1
. By a similar reasoning, we have
that (u, v
1
, v
2
) is a delocalizing triple of C
′
. How-
ever, ig( f
′
) has a new positive cycle v
1
⊕
−→ v
1
that
has no delocalizing triple in ig( f
′
). Of course, since
|w
−
| = |w
+
| = 1, the positive cycle w
⊖
−→ v
1
⊖
−→ w has
no killing triple in ig( f ). Hence, U
0
∩ {w, v
1
} ̸=
/
0 in
ig( f ). If v
1
∈ U
0
, then v
1
∈ U
0
in ig( f
′
). If v
1
̸∈ U
0
and w ∈ U
0
, then we replace w by v
1
in U
0
. The size of
U
0
does not change, but it does not miss any another
positive cycle without a delocalizing triple because w
cannot belong to any another positive cycle in ig( f ).
At the end, we always have a subset of vertices
(say U
1
) that intersects every positive cycle without a
delocalizing triple in ig( f
′
) and |U
1
| = |U
0
|.
By the reduction results w.r.t. fixed points (Veliz-
Cuba, 2011) and the fact that (ww, ⊖) is not an arc
of ig( f ), there is a bijection between the set of fixed
points of f and that of f
′
. By Theorem 19, f
′
has at
most 2
|U
1
|
fixed points. It follows that f has at most
2
|U
0
|
fixed points.
Example 5. Consider two signed directed graphs:
G
′
1
and G
′
2
(see Figures 4(a) and 4(b), respectively).
G
′
1
(resp. G
′
2
) is the new graph transformed from G
1
(resp. G
2
) of Example 4 by following the transforma-
tion shown in the proof of Theorem 20. In G
1
, (a,d, c)
is a killing triple of positive cycle c
⊖
−→ d
⊖
−→ c, and
in G
′
1
, (a, d, c) becomes a delocalizing tripple of this
positive cycle. In G
2
, (c, c, a) is a killing triple of pos-
itive cycle a
⊖
−→ b
⊖
−→ c
⊖
−→ d
⊖
−→ a, and in G
′
2
, (c, c, a)
becomes a delocalizing triple of this positive cycle.
The new positive cycle c
⊕
−→ c in G
′
2
has no delocaliz-
ing triple.
a
c
d
⊖
⊖
⊕
⊖
(a) .
a
b
c
d
⊕
⊖ ⊖
⊖
⊖
⊖
(b) .
Figure 4: (a) G
′
1
and (b) G
′
2
. These graphs are considered in
Example 5.
Theorem 21. Given an AF A . Let U
0
be a subset
of vertices that intersects every positive cycle without
a killing triple of ag(A). Then A has at most 2
|U
0
|
stable extensions.
Proof. It straightforwardly follows from Theorem 20,
Proposition 1, and Corollary 1.
It is worth noting that Theorem 20 is also new in
the BN theory.
6 CONCLUSION
In this work, we established the connection between
AFs and BNs. More specifically, we showed that the
attack graph of an AF coincides with the influence
graph of its encoded BN, and preferred (resp. sta-
ble) extensions of the AF one-to-one correspond to
minimal trap spaces (resp. fixed points) of the en-
coded BN. We defined a new concept of complete trap
space and showed that complete extensions of the AF
one-to-one correpond to complete trap spaces of the
BN, and in particular the grounded extension of the
AF one-to-one corresponds to the percolation of the
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
754

whole-space trap space of the BN. We also showed a
more general characterization of complete trap spaces
in BNs. We then applied this connection to the graphi-
cal analysis of AFs: showing graphical conditions for
properties on preferred, stable, and complete exten-
sions. In particular, we showed new upper bounds
based on positive feedback vertex sets for the num-
bers of stable, preferred, and complete extensions. An
advantage of the above approach is that we only need
to focus on dynamical properties of BNs when study-
ing extensions in AFs, openning the great potential
to obtain more improved theoretical results regarding
the graphical analysis of AFs.
REFERENCES
Aracena, J. (2008). Maximum number of fixed points
in regulatory Boolean networks. Bull. Math. Biol.,
70(5):1398–1409.
Azpeitia, E., Guti
´
errez, S. M., Rosenblueth, D. A., and
Zapata, O. (2024). Bridging abstract dialectical ar-
gumentation and Boolean gene regulation. CoRR,
abs/2407.06106.
Baroni, P., Toni, F., and Verheij, B. (2020). On the ac-
ceptability of arguments and its fundamental role in
nonmonotonic reasoning, logic programming and n-
person games: 25 years later. Argument Comput.,
11(1-2):1–14.
Baumann, R., Dvor
´
ak, W., Linsbichler, T., Strass, H., and
Woltran, S. (2014). Compact argumentation frame-
works. In Proc. of ECAI, pages 69–74. IOS Press.
Baumann, R. and Strass, H. (2013). On the maximal and av-
erage numbers of stable extensions. In Proc. of TAFA,
pages 111–126. Springer.
Baumann, R. and Strass, H. (2015). Open problems in ab-
stract argumentation. In Advances in Knowledge Rep-
resentation, Logic Programming, and Abstract Argu-
mentation - Essays Dedicated to Gerhard Brewka on
the Occasion of His 60th Birthday, pages 325–339.
Springer.
Baumann, R. and Ulbricht, M. (2021). On cycles, attackers
and supporters - A contribution to the investigation of
dynamics in abstract argumentation. In Proc. of IJ-
CAI, pages 1780–1786. ijcai.org.
Caminada, M., S
´
a, S., Alc
ˆ
antara, J. F. L., and Dvor
´
ak, W.
(2015). On the equivalence between logic program-
ming semantics and argumentation semantics. Int. J.
Approx. Reason., 58:87–111.
Caminada, M. W. A. and Gabbay, D. M. (2009). A logical
account of formal argumentation. Stud Logica, 93(2-
3):109–145.
Charwat, G., Dvor
´
ak, W., Gaggl, S. A., Wallner, J. P., and
Woltran, S. (2015). Methods for solving reasoning
problems in abstract argumentation - A survey. Artif.
Intell., 220:28–63.
Coste-Marquis, S., Devred, C., and Marquis, P. (2005).
Symmetric argumentation frameworks. In Proc. of
ECSQARU, pages 317–328. Springer.
Dewoprabowo, R., Fichte, J. K., Gorczyca, P. J., and
Hecher, M. (2022). A practical account into count-
ing Dung’s extensions by dynamic programming. In
Proc. of LPNMR, pages 387–400. Springer.
Dimopoulos, Y., Dvor
´
ak, W., and K
¨
onig, M. (2024). Con-
necting abstract argumentation and Boolean networks.
In Proc. of COMMA, pages 85–96. IOS Press.
Dimopoulos, Y. and Torres, A. (1996). Graph theoreti-
cal structures in logic programs and default theories.
Theor. Comput. Sci., 170(1-2):209–244.
Dung, P. M. (1995). On the acceptability of arguments
and its fundamental role in nonmonotonic reasoning,
logic programming and n-person games. Artif. Intell.,
77(2):321–358.
Dunne, P. E. (2007). Computational properties of argument
systems satisfying graph-theoretic constraints. Artif.
Intell., 171(10-15):701–729.
Dunne, P. E., Dvor
´
ak, W., Linsbichler, T., and Woltran, S.
(2015). Characteristics of multiple viewpoints in ab-
stract argumentation. Artif. Intell., 228:153–178.
Elaroussi, M., Nourine, L., Radjef, M. S., and Vilmin, S.
(2023). On the preferred extensions of argumentation
frameworks: Bijections with naive sets. Inf. Process.
Lett., 181:106354.
Gaspers, S. and Li, R. (2019). Enumeration of preferred
extensions in almost oriented digraphs. In Proc. of
MFCS, pages 74:1–74:15. Schloss Dagstuhl - Leibniz-
Zentrum f
¨
ur Informatik.
Heyninck, J., Knorr, M., and Leite, J. (2024). Abstract di-
alectical frameworks are Boolean networks. In Do-
daro, C., Gupta, G., and Martinez, M. V., editors,
Proc. of LPNMR, pages 98–111. Springer.
Kauffman, S. A. (1969). Metabolic stability and epigenesis
in randomly constructed genetic nets. J. Theor. Biol.,
22(3):437–467.
Klarner, H., Bockmayr, A., and Siebert, H. (2015). Com-
puting maximal and minimal trap spaces of Boolean
networks. Nat. Comput., 14(4):535–544.
Kr
¨
oll, M., Pichler, R., and Woltran, S. (2017). On the com-
plexity of enumerating the extensions of abstract ar-
gumentation frameworks. In Proc. of IJCAI, pages
1145–1152. ijcai.org.
Nieves, J. C., Cort
´
es, U., and Osorio, M. (2008). Preferred
extensions as stable models. Theory Pract. Log. Pro-
gram., 8(4):527–543.
Nouioua, F. and Risch, V. (2012). A reconstruction of
abstract argumentation admissible semantics into de-
faults and answer sets programming. In Proc. of
ICAART, pages 237–242. SciTePress.
Obiedkov, S. and Sertkaya, B. (2023). Computing stable
extensions of argumentation frameworks using formal
concept analysis. In Proc. of JELIA, pages 176–191.
Springer.
Paulev
´
e, L. and Richard, A. (2012). Static analysis of
Boolean networks based on interaction graphs: a sur-
vey. Electron. Notes Theor. Comput. Sci., 284:93–104.
Pollock, J. L. (1987). Defeasible reasoning. Cogn. Sci.,
11(4):481–518.
Graphical Analysis of Abstract Argumentation Frameworks via Boolean Networks
755

Pollock, J. L. (1991a). Self-defeating arguments. Minds
Mach., 1(4):367–392.
Pollock, J. L. (1991b). A theory of defeasible reasoning.
Int. J. Intell. Syst., 6(1):33–54.
Richard, A. (2009). Positive circuits and maximal number
of fixed points in discrete dynamical systems. Discret.
Appl. Math., 157(15):3281–3288.
Richard, A. (2010). Negative circuits and sustained oscilla-
tions in asynchronous automata networks. Adv. Appl.
Math., 44(4):378–392.
Richard, A. (2019). Positive and negative cycles in Boolean
networks. J. Theor. Biol., 463:67–76.
Richard, A. and Comet, J. (2007). Necessary conditions for
multistationarity in discrete dynamical systems. Dis-
cret. Appl. Math., 155(18):2403–2413.
Richard, A. and Ruet, P. (2013). From kernels in directed
graphs to fixed points and negative cycles in Boolean
networks. Discret. Appl. Math., 161(7-8):1106–1117.
Rozum, J. C., G
´
omez Tejeda Za
˜
nudo, J., Gan, X., Deritei,
D., and Albert, R. (2021). Parity and time reversal
elucidate both decision-making in empirical models
and attractor scaling in critical Boolean networks. Sci.
Adv., 7(29):eabf8124.
Schwab, J. D., K
¨
uhlwein, S. D., Ikonomi, N., K
¨
uhl, M., and
Kestler, H. A. (2020). Concepts in Boolean network
modeling: What do they all mean? Comput. Struct.
Biotechnol. J., 18:571–582.
Thimm, M., Cerutti, F., and Vallati, M. (2021). Skeptical
reasoning with preferred semantics in abstract argu-
mentation without computing preferred extensions. In
Proc. of IJCAI, pages 2069–2075. ijcai.org.
Toulmin, S. (1958). The Uses of Argument. Cambridge
University Press, Cambridge, England.
Trinh, G. V., Benhamou, B., Pastva, S., and Soliman,
S. (2024a). Scalable enumeration of trap spaces in
Boolean networks via answer set programming. In
Proc. of AAAI, pages 10714–10722. AAAI Press.
Trinh, V. and Benhamou, B. (2024). Static analysis
of logic programs via Boolean networks. CoRR,
abs/2407.09015.
Trinh, V.-G., Benhamou, B., and Soliman, S. (2023). Trap
spaces of Boolean networks are conflict-free siphons
of their Petri net encoding. Theor. Comput. Sci.,
971:114073.
Trinh, V.-G., Benhamou, B., Soliman, S., and Fages, F.
(2024b). Graphical conditions for the existence, unic-
ity and number of regular models. In Proc. of ICLP,
pages 175–186.
Trinh, V.-G., Park, K. H., Pastva, S., and Rozum, J. C.
(2024c). Mapping the attractor landscape of Boolean
networks. bioRxiv.
Ulbricht, M. (2021). On the maximal number of complete
extensions in abstract argumentation frameworks. In
Proc. of KR, pages 707–711.
Veliz-Cuba, A. (2011). Reduction of Boolean network mod-
els. J. Theor. Biol., 289:167–172.
Veliz-Cuba, A., Buschur, K., Hamershock, R., Kniss, A.,
Wolff, E., and Laubenbacher, R. (2012). AND-NOT
logic framework for steady state analysis of Boolean
network models.
Yun, B., Croitoru, M., Vesic, S., and Bisquert, P. (2017).
Graph theoretical properties of logic based argumen-
tation frameworks: Proofs and general results. In
Proc. of GKR, pages 118–138. Springer.
ICAART 2025 - 17th International Conference on Agents and Artificial Intelligence
756