Bus Arrival Time Prediction via Hybrid LSTM Using GPS-Derived

Run and Dwell Times

Aigerim Mansurova

, Aiganym Mansurova

and Aivar Sakhipov

Astana IT University, Mangilik El 55/11, Astana, Kazakhstan

Keywords: Public Transportation System, Bus Arrival Time Prediction, Long Short-Term Memory, GPS Trajectory Data,

Urban Traffic Conditions.

Abstract: Accurate bus arrival time prediction is essential for improving the reliability and efficiency of public

transportation systems. While existing models often rely on complex ensemble architectures or extensive

contextual data, this study explores a simplified approach using a hybrid Long Short-Term Memory (LSTM)

model. The model processes sequential features, such as stop IDs, run times, and dwell times, through LSTM

layers while integrating contextual information, such as trip start hour and day of the week, via dense layers.

Comprehensive experiments on GPS data from buses in Kandy, Sri Lanka, demonstrate the model’s superior

performance against state-of-the-art baselines. The proposed model achieves a Mean Absolute Error (MAE)

of 13.4 seconds, a Mean Absolute Percentage Error (MAPE) of 10.32%, and a Root Mean Square Error

(RMSE) of 24.26 seconds, significantly outperforming alternative methods.

1 INTRODUCTION

Public buses are an essential mode of transportation,

supporting daily commutes for work and leisure

(Levin, 2019). However, challenges like

overcrowding and irregular service schedules remain

prevalent. Accurate prediction of bus travel times is

crucial for intelligent transportation systems (ITS),

enabling enhanced service reliability, passenger

satisfaction, and operational efficiency. The advent of

Automatic Vehicle Location (AVL) systems has

marked a new era in analyzing travel time reliability.

These systems, which typically integrate GPS

technology and other location-tracking methods,

provide real-time vehicle position data with

timestamps, forming a foundational component of

Intelligent Transportation Systems (ITS). By

generating vast amounts of bus trajectory data, AVL

enables precise fleet tracking and monitoring. Despite

these advancements, discrepancies between

estimated and actual arrival times persist, impacting

service quality and passenger satisfaction.

Recent advancements in bus arrival time

prediction models have focused on enhancing

https://orcid.org/0009-0003-1978-9574

https://orcid.org/0009-0007-9076-0722

https://orcid.org/0000-0003-1045-4199

accuracy by decomposing total travel time into its

components—dwell time (time spent at stops while

passengers board and alight) and run time (time spent

traveling between stops) (Xie et al., 2021; Osman et

al., 2021). These efforts emphasize hybrid modeling

techniques and multi-model approaches to address

the complexities of urban traffic conditions.

Hybrid models have gained prominence for their

ability to leverage the strengths of different modeling

techniques. Yang et al. (2022) proposed a hybrid

approach combining Simple Moving Averages

(SMA) and Long Short-Term Memory (LSTM)

networks, treating dwell and run times as separate

prediction targets. This method significantly

improved accuracy, achieving a Mean Absolute

Percentage Error (MAPE) reduction to 23.45%.

Similarly, Zeng et al. (2019) developed a hybrid

LSTM model that integrates historical cruising

speeds with real-time traffic factors, demonstrating its

effectiveness in adapting to dynamic urban traffic

conditions.

Multi-model ensemble methods have also shown

promise. Petersen et al. (2019) utilized a multi-output

ensemble combining convolutional layers for spatial

514

Mansurova, A., Mansurova, A. and Sakhipov, A.

Bus Arrival Time Prediction via Hybrid LSTM Using GPS-Derived Run and Dwell Times.

DOI: 10.5220/0013349200003941

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 514-519

ISBN: 978-989-758-745-0; ISSN: 2184-495X

feature extraction and LSTM layers for capturing

temporal dependencies. Although this model

outperformed single-step predictions, its

computational complexity posed challenges for real-

time applications. Ratneswaran and Thayasivam

(2023) further explored ensemble methods by

integrating ConvLSTM and XGBoost models, which

proved effective in high-variability traffic scenarios.

However, their reliance on fine-grained feature

engineering limited scalability.

The balance between simplicity and complexity in

model design is another central theme. Early studies

favored simpler methods, such as Kalman filters and

historical averages (Chien and Kuchipudi, 2003),

which remain advantageous for real-time or resource-

constrained settings. However, modern research leans

toward complex architectures, including hybrid and

ensemble models, to address the variability and

unpredictability of traffic conditions.

This paper contributes to the literature by offering

a simplified yet effective framework that directly

predicts bus arrival time using a hybrid LSTM model.

The approach eliminates the need for complex

ensemble architectures by utilizing data with travel

time components already divided into dwell times and

run times. Unlike the models that integrate external

factors such as traffic, passenger flow, or weather, our

approach relies solely on core travel time data. This

ensures adaptability in data-sparse environments

while maintaining real-time applicability and

computational efficiency.

The rest of the paper is structured as follows:

Section 2 provides a detailed explanation of the

proposed methodology, including an overview of the

data, feature engineering, the model development

process, as well as outlines the experimental design,

describing the evaluation metrics and baselines.

Section 3 presents the results, comparing the hybrid

model's performance with that of the baseline models.

Finally, Section 4 concludes the paper by

summarizing the findings, discussing practical

implications, and suggesting potential directions for

future research.

2 MATERIALS AND METHODS

2.1 Dataset

The dataset utilized in this study was obtained from

the AVL system installed on public buses operating

along Route No. 654 in Kandy, Sri Lanka, connecting

Kandy and Digana terminals with 30 bus stops. The

dataset comprises 14,128 recorded trips collected

over nine months, from October 1, 2021, to February

28, 2022. Bus location data was captured at a 15-

second sampling interval.

The raw GPS data, as provided by Ratneswaran

and Thayasivam (2023), was processed to obtain

segment (a route section between two consecutive bus

stops) running times and dwell times. To ensure a

robust dataset for analysis, data collection was

performed between 6:00 a.m. and 7:00 p.m., covering

morning and evening peak hours, moderate

congestion periods, and off-peak free-flow

conditions. This enables the study to capture

variations in travel time under different traffic

conditions, ensuring that the dataset reflects real-

world operational variability. The original data is

divided into three separate datasets, each stored as a

CSV file, as shown in Table 1.

Table 1: Structure of the original data.

Name Description Attributes

bus_trips_

654.csv

Trip-level

travel time

data

trip_id, deviceid,

start_terminal,

end_terminal,

start_time, end_time,

duration

bus_dwell

_times_65

4.csv

Stop-level

dwell time

data

trip_id, deviceid,

bus_stop, arrival_time,

departure_time,

dwell

time

seconds

bus_runni

ng_times_

654.csv

Travel time

between

consecutive

sto

trip_id, deviceid,

segment, start_time,

end_time,

run

time

seconds

bus_stops

_and_term

inals_654.

csv

Bus stop

locations and

route mapping

stop_id, route_id,

direction, address,

latitude, longitude

To prepare the dataset for use in this study,

essential data cleaning and feature engineering were

undergone. Stop locations, represented by the

variables ‘start_point’ and ‘end_point,’ were

engineered through the integration of data from the

bus dwell times and running times datasets. For each

trip, the initial terminal, either ‘T1’ or ‘T2,’ was

assigned based on the travel direction, and subsequent

stops were extracted from the dwell dataset. To

standardize their representation for use in machine

learning models, these stops were encoded into

numerical values using a label encoding technique.

Temporal features such as ‘start_hour’ and

‘day_of_week’ were engineered to capture time-

based patterns. The target variable, ‘travel_time’ was

calculated as the sum of ‘run_time_in_seconds’ and

‘dwell_time_in_seconds,’ representing the total trip

Bus Arrival Time Prediction via Hybrid LSTM Using GPS-Derived Run and Dwell Times

515

segment duration. Table 2 presents an overview of the

dataset, including attribute definitions and a sample

data entry.

Table 2: Dataset overview.

Attribute Description Example

id Unique record identifier 877965

trip_id Unique trip identifier 1

date Date of the trip 2021-10-01

deviceid

Unique bus device

identifie

262

direction Travel direction indicator 1

segment Route segment number 1.0

start_point Departure stop identifier T1

end_point Arrival stop identifier 101

start_time Start time of the segment 06:39:49

run_time_in

seconds

Time taken to travel

etween sto

dwell_time_

in_seconds

Time spent waiting at a

stop

arrival_time Arrival time at the stop 06:40:58

departure_ti

Departure time from the

sto

06:42:12

travel_time

Total travel time (run time

+ dwell time

)

143

For sequence-based analysis, multi-feature

sequences of stop IDs, running times, and dwell times

were created and padded to a fixed length to ensure

consistency for LSTM input.

The dataset was partitioned into training and

testing subsets, with 80% of the trips assigned to the

training set and the remaining 20% allocated to the

testing set. The split was performed in chronological

order.

2.2 Model Development

In this study, a hybrid machine learning model was

developed to predict travel time between successive

bus stops. The model was developed in Python

utilizing the Keras framework and trained with the

Adam optimizer. Sequential features, such as stop

IDs, running times, and dwell times, were processed

using a Long Short-Term Memory (LSTM) network,

leveraging its strength in modeling temporal

dependencies. Non-sequential features, including the

day of the week and trip start hour, were handled

through fully connected dense layers to capture

contextual information (see Figure 1). The dependent

variable in this study is bus segment travel time,

defined as the total duration required for a bus to

travel between two consecutive stops. The

architecture combined these processed inputs into a

unified representation, facilitating the modeling of

temporal and contextual aspects of travel time.

Figure 1: The layers of the proposed model.

Dropout layers and batch normalization were

incorporated to mitigate overfitting and enhance

model generalization. This integration of diverse

input types allows the model to achieve high accuracy

with minimal reliance on extensive feature

engineering.

2.3 Experiments

The feasibility of enhancing the accuracy of the bus

travel duration prediction between bus stops was

investigated using baselines including a multi-model

ensemble approach (Ratneswaran & Thayasivam,

2023), a ConvLSTM segment-based model (Xie et

al., 2021), an XGBoost segment-based model (Zhu et

al., 2022), a multi-model methodology integrating

ConvLSTM with Exponential Smoothing (Petersen et

al., 2019), and two standalone ConvLSTM models as

detailed in (Wu et al., 2020). All of these baselines

were evaluated on the same dataset in the work of

Ratneswaran and Thayasivam (2023).

The evaluation of the proposed model and the

baseline methods was conducted using three key

metrics: (1) Mean Absolute Error (MAE), (2) Mean

Absolute Percentage Error (MAPE), and (3) Root

Mean Square Error (RMSE). These metrics are

defined in equations (1) to (3), where 𝑦



indicates the

actual travel times, 𝑦



represents the predicted travel

times, and 𝑛 refers to the number of samples.

𝑀𝐴𝐸

𝑛



𝑦



𝑦









)

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

516

𝑀𝐴𝑃𝐸

𝑛



𝑦



𝑦



𝑦









∙ 100

(2)

𝑅𝑀𝑆𝐸





𝑛

𝑦



𝑦













(3)

3 RESULTS

To determine the optimal sequence length

(max_sequence_length parameter) for the LSTM-

based architecture, experiments were conducted with

sequence lengths varying between 2 and 14. Figure 2

demonstrates how the evaluation metrics change with

sequence length, highlighting its impact on model

performance.

While a sequence length of 2 yields lower MAE

and MAPE, it exhibits a higher RMSE, indicating

greater variability in prediction errors. This suggests

that shorter sequences may lead to less stable

predictions with occasional large deviations. In

contrast, a sequence length of 4 strikes a balance

between error minimization and predictive stability.

By incorporating a slightly longer historical context,

it reduces the impact of outliers and enhances the

model’s robustness, making it the optimal choice for

reliable performance.

Figure 2: Impact of sequence length on model performance.

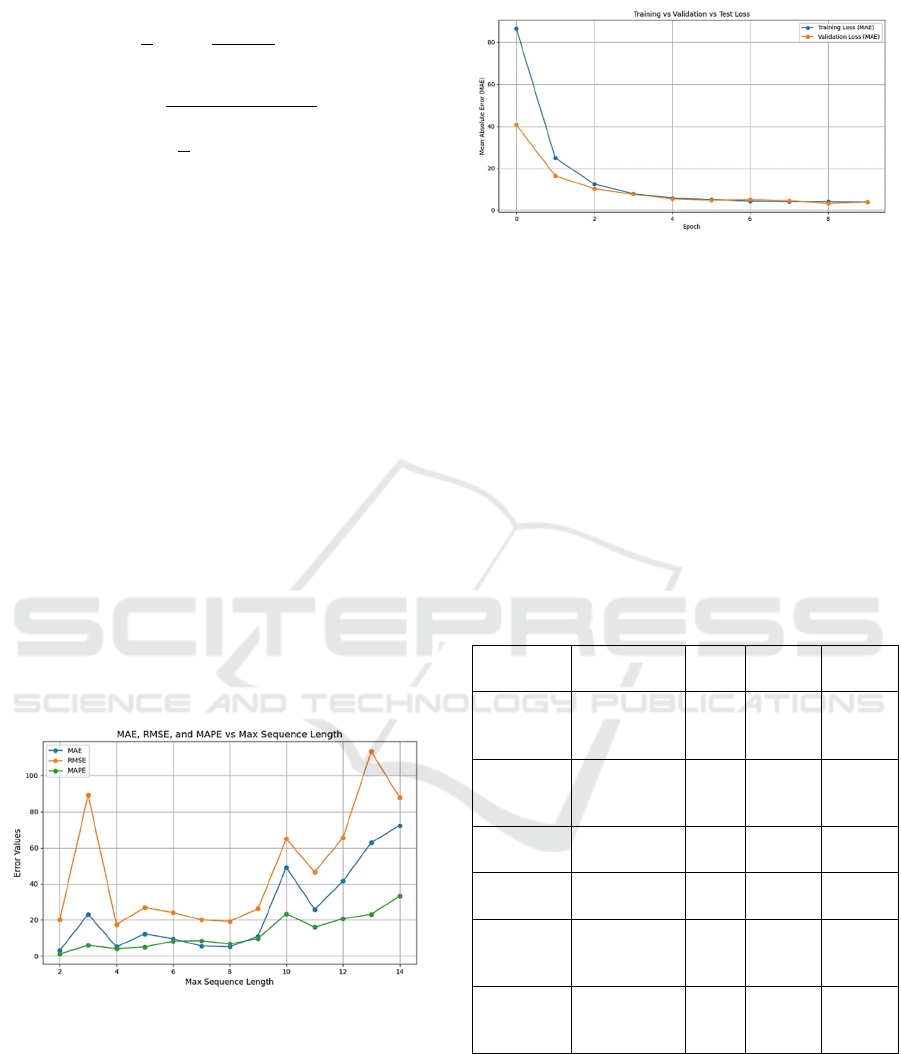
Training and validation losses (MAE) dropped

quickly in the first few epochs and stabilized by the

3rd epoch (Figure 3). After 5 epoch, validation loss

stopped improving while training loss continued to

decrease slightly, indicating overfitting. Thus, the 3rd

epoch was chosen for optimal generalization.

Figure 3: Training and Validation Loss.

The results in Table 3 demonstrate the superior

performance of the proposed hybrid model compared

to baseline methods in predicting bus travel times.

The proposed model achieves a significantly lower

MAE of 13.4 seconds, outperforming the closest

baseline, the multi-model ensemble approach, which

has an MAE of 36.2 seconds. Similarly, the MAPE

for the proposed model is reduced to 10.32%, a

substantial improvement over the lowest baseline

MAPE of 19.01%. For RMSE, the proposed model

achieves 24.26 seconds, markedly lower than the best

baseline performance of 58.2 seconds.

Table 3: Performance comparison of the proposed model

and baseline methods in terms of MAE, MAPE, and RMSE.

Model Ref. MAE

(s)

MAPE

(%)

RMSE

(s)

ConvLSTM

segment-

based

Xie et al., 2021 43.1 20.50 71.4

XGBoost

segment-

based

Zhu et al.,

2022

41.0 23.02 62.3

ConvLSTM

+ ES

Petersen et al.,

2019

39.2 19.12 63.5

ConvLSTM

multi-model

Wu et al., 2020 39.7 20.64 61.7

Multi-model

ensemble

Ratneswaran &

Thayasivam,

2023

36.2 19.01 58.2

Proposed

Hybrid

model

this work 13.4 10.32 24.26

To improve transparency concerning the scale of

segment travel times, it is important to clarify that

segment durations are influenced by factors such as

traffic conditions, route lengths, and stop

characteristics. On average, segment travel times

range from 168 to 274 seconds, with variations

primarily driven by congestion levels and stop

densities. This range ensures that prediction errors, as

Bus Arrival Time Prediction via Hybrid LSTM Using GPS-Derived Run and Dwell Times

517

measured by the Mean Absolute Error (MAE = 13.4

seconds), are evaluated within a meaningful and

practical context. To further enhance clarity,

segment-wise travel time distributions are explicitly

reported in Table 4.

Table 4: Segment travel time distribution.

Segment

Length (km)

Mean Travel

Time (s)

Standard

Deviation (s)

(0 - 0.5] 168.3 66.1

(0.5 – 1] 218.9 77.1

>1 274.4 82.0

4 CONCLUSIONS

The results of this study emphasize the effectiveness

of the hybrid architecture in combining sequential

features, such as stop IDs and running times, with

non-sequential contextual inputs, such as the day of

the week and trip start hour. This integration

leverages the temporal modeling capabilities of

LSTM networks and the contextual feature extraction

of dense layers to achieve exceptional accuracy. The

sequence-based LSTM model dynamically refines

estimates as new data becomes available, mitigating

error accumulation over the course of a journey. The

proposed model’s performance underscores its

superiority over conventional methods, including

standalone models and ensemble approaches. The

model achieves a MAE of 13.4 seconds, MAPE of

10.32% and RMSE of 24.26% making it suitable for

travel time prediction in smart transportation systems.

The dataset used in this study was obtained from

prior research and underwent preprocessing by the

original authors, including the removal of outliers.

While the proposed hybrid model demonstrates

strong accuracy with this preprocessed data, future

validation using less preprocessed datasets is crucial

to assess the model's robustness and its applicability

across diverse real-world scenarios. Such efforts will

help determine the model's adaptability and

effectiveness in varying contexts where data may be

noisier or exhibit different patterns.

While this study focuses on historical data for

training and evaluation, future research will explore

real-time integration to further enhance predictive

adaptability. This step-by-step refinement enables the

model to remain robust, ensuring that travel time

predictions remain accurate even in varying

operational conditions.

ACKNOWLEDGEMENTS

This research has been funded by the Committee of

Science of the Ministry of Science and Higher

Education of the Republic of Kazakhstan (Grant

No.BR24992852 “Intelligent models and methods of

Smart City digital ecosystem for sustainable

development and the citizens’ quality of life

improvement”).

REFERENCES

Levin, L. (2019). How may public transport influence the

practice of everyday life among younger and older

people and how may their practices influence public

transport?. Social Sciences, 8(3), 96.

Yang, Z., Lam, C. T., & Ng, B. K. (2022). Multi-Model Bus

Arrival Time Prediction using Real-Time Online

Information. In 2022 IEEE 22nd International

Conference on Communication Technology, ICCT

2022 (pp. 1918-1922). (International Conference on

Communication Technology Proceedings, ICCT; Vol.

2022-November-November). Institute of Electrical and

Electronics Engineers Inc.. https://doi.org/10.1109/

ICCT56141.2022.10072901

Lingqiu, Z., Guangyan, H., Qingwen, H., Lei, Y., Fengxi,

L., & Lidong, C. (2019, August). A LSTM based bus

arrival time prediction method. In 2019 ieee

smartworld, ubiquitous intelligence & computing,

advanced & trusted computing, scalable computing &

communications, cloud & big data computing, internet

of people and smart city innovation (smartworld/

scalcom/uic/atc/cbdcom/iop/sci) (pp. 544-549). IEEE.

Petersen, N. C., Rodrigues, F., & Pereira, F. C. (2019).

Multi-output deep learning for bus arrival time

predictions. Transportation Research Procedia, 41,

138-145.

Ratneswaran, S., & Thayasivam, U. (2023, September). An

Improved Bus Travel Time Prediction Using Multi-

Model Ensemble Approach for Heterogeneous Traffic

Conditions. In 2023 IEEE 26th International

Conference on Intelligent Transportation Systems

(ITSC) (pp. 2410-2415). IEEE.

Chien, S. I. J., & Kuchipudi, C. M. (2003). Dynamic travel

time prediction with real-time and historic data. Journal

of Transportation Engineering, 129(6), 608-616.

https://doi.org/10.1061/(ASCE)0733-

947X(2003)129:6(608)

Xie, Z. Y., He, Y. R., Chen, C. C., Li, Q. Q., & Wu, C. C.

(2021). Multistep prediction of bus arrival time with the

recurrent neural network. Mathematical Problems in

Engineering, 2021(1), 6636367.

Osman, O., Rakha, H., & Mittal, A. (2021). Application of

long short term memory networks for long-and short-

term bus travel time prediction.

Zhu, L., Shu, S., & Zou, L. (2022). XGBoost‐Based Travel

Time Prediction between Bus Stations and Analysis of

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

518

Influencing Factors. Wireless Communications and

Mobile Computing, 2022(1), 3504704.

Wu, J., Wu, Q., Shen, J., & Cai, C. (2020). Towards

attention-based convolutional long short-term memory

for travel time prediction of bus journeys. Sensors,

20(12), 3354.

Bus Arrival Time Prediction via Hybrid LSTM Using GPS-Derived Run and Dwell Times

519