Towards an Approach for Project-Library Recommendation Based on
Graph Normalization
Abhinav Jamwal
a
and Sandeep Kumar
b
Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Roorkee, India
Keywords:
Graph Laplacian, Normalization, GNN, Node Classification, Third-Party Library Recommendation.
Abstract:
The performance of project-library recommendation systems depends on the choice of graph normalization
techniques. This work explores two primary normalization schemes within a knowledge graph - enhanced
project - library recommendation system: symmetric normalized Laplacian (SNL) and random walk normal-
ized Laplacian (RWL). Experimental results show that RWL consistently delivers better performance in key
metrics, including mean precision (MP), mean recall (MR), and mean F1 score (MF), particularly in sparse
datasets. Although SNL performs well in denser datasets, its effectiveness decreases with increasing spar-
sity. Furthermore, loss curves for collaborative filtering (CF) and knowledge graph (KG) tasks indicate that
RWL converges faster and shows greater stability. These findings establish RWL as a reliable technique for
improving GNN-based recommendation systems, especially in sparse and complex project-library interaction
scenarios.
1 INTRODUCTION
Deep learning has transformed numerous domains,
particularly with the success of convolutional neural
networks (CNNs) (LeCun et al., 1998). While CNNs
excel at modeling structured grid-like data, graph neu-
ral networks (GNNs)(Wu et al., 2022) have emerged
to address non-Euclidean data structures, such as
graphs, enabling advances in fields such as protein
structure prediction (Mastropietro et al., 2023), traf-
fic planning (Ye et al., 2023), and recommendation
systems (Isinkaye et al., 2015).
In recommendation systems, graph-based models
have gained significant attention for their ability to
represent and exploit complex user-item interactions.
PyRec(Li et al., 2024), a framework that uses graph
neural networks (GNNs)(Zhou et al., 2020) with in-
tegrated knowledge graphs, has shown promising re-
sults in third-party library recommendation (TPL)
tasks. By encoding user-library relationships and us-
ing knowledge graphs for additional contextual in-
formation, PyRec(Li et al., 2024) improves the pre-
cision and relevance of recommendations. However,
its reliance on GNN-based methodologies highlights
a crucial challenge: the sensitivity of GNN perfor-
a
https://orcid.org/0000-0002-0213-3590
b
https://orcid.org/0000-0002-3250-4866
mance to the choice of adjacency matrix normaliza-
tion schemes.
Normalization schemes are pivotal in GNN-based
models as they scale node degrees, balance informa-
tion propagation, and preserve graph topology dur-
ing message passing. Despite their importance, the
impact of normalization schemes on TPL recommen-
dation tasks in PyRec(Li et al., 2024) has not been
systematically investigated. This aspect is essential
for optimizing graph-based recommendation systems
and addressing challenges such as scalability, noise
robustness, and sparsity.
Motivated by these considerations, this research
investigates the effect of different adjacency matrix
normalization techniques on PyRec(Li et al., 2024)
performance. By analyzing how these schemes influ-
ence metrics such as precision, recall, and NDCG, we
aim to provide information on the design of robust
and efficient GNN-based recommendation systems.
The main contributions of this work are:
• We systematically explore the two primary
normalization schemes, Symmetric Normalized
Laplacian (SNL) and Random Walk Normalized
Laplacian (RWL) - on the performance of project-
library recommendation, focusing on their effects
on key metrics such as precision, recall, F1 score,
MAP, and MRR.
• We analyze the performance of these normaliza-
120
Jamwal, A. and Kumar, S.
Towards an Approach for Project-Library Recommendation Based on Graph Normalization.
DOI: 10.5220/0013351900003928
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 20th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2025), pages 120-127
ISBN: 978-989-758-742-9; ISSN: 2184-4895
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

tion schemes in varying levels of data sparsity,
demonstrating the robustness and effectiveness of
RWL compared to SNL in handling sparse and in-
complete datasets.
• We examine loss curves for Collaborative Filter-
ing (CF) and Knowledge Graph (KG) tasks, high-
lighting the faster convergence and stability of
RWL over SNL.
• We provide actionable insights and practical rec-
ommendations for selecting normalization tech-
niques to optimize graph-based recommendation
systems, particularly in the context of third-party
library usage and sparse datasets.
The remainder of this paper is organized as fol-
lows. Section 2 reviews the literature on graph neural
networks, knowledge graphs, and normalization tech-
niques. Section 3 describes the experimental setup
and methods for evaluating normalization schemes in
PyRec. Section 4 presents a detailed analysis of the
results. Finally, Section 5 summarizes the findings
and suggests future research directions.
2 RELATED WORK
Graph Neural Networks (GNNs) have emerged as
one of the most innovative approaches in machine
learning and artificial intelligence, capable of address-
ing problems involving graph-structured data by en-
abling effective information exchange between graph
nodes. GNNs excel at modeling complex dependen-
cies and relationships inherent in graph representa-
tions(Zhou et al., 2020). Over time, numerous ar-
chitectures have been developed to cater to diverse
use cases. Prominent examples include Graph Convo-
lutional Networks (GCNs)(Kipf and Welling, 2016),
Graph Attention Networks (GATs)(Veli
ˇ
ckovi
´
c et al.,
2017), and Graph Isomorphism Networks (GINs)(Xu
et al., 2018), all of which have been successfully ap-
plied in various domains. Zhou et al.(Zhou et al.,
2020) categorized GNNs into four classes: RGNNs,
GCNNs, ST-GCNs, and GraphAEs, providing a struc-
tured overview of their functionalities. Khemani et
al.(Asif et al., 2021) conducted a comprehensive re-
view of GNN architectures, offering valuable insights
into their design principles, real-world applications,
and benchmark datasets, laying a strong foundation
for future research.
Recent breakthroughs in GNN have pointed out
that low-rank approximation methods effectively en-
hance models’ efficiency and scalability. The low-
rank approximation hypothesis assumes that compli-
cated graph structures can be effectively represented
using lower-dimensional embeddings without signif-
icant loss of information. In addition, this approach
allows for the compression of node and edge fea-
tures into concise latent spaces, reducing computa-
tional overhead. For example, the LRGA mecha-
nism was proposed to incorporate low-rank approx-
imations into GNNs so that global attention compu-
tation can be efficiently and scalably performed us-
ing matrix-vector multiplication of low-rank matri-
ces (Puny et al., 2020). Empirical studies (Yang
et al., 2024; Zhang et al., 2018) demonstrate that
this type of low-rank representation can preserve or
even enhance model performance, since these meth-
ods preserve crucial structural patterns while remov-
ing redundancy. This objective has been consider-
ably helped by using low-rank SVD and random-
ized low-rank matrix approximation techniques(Wu
et al., 2010). It is a promising direction in developing
scalable graph-based models, mainly for large-scale
datasets where traditional methods can be computa-
tionally strained.
Considering these low-dimensional representa-
tions, the arising of the Laplacian matrix as a basic
tool in graph theory for graph representation analy-
sis is of great importance. In fact, regarding the en-
coding of graph topology, a wide range of applica-
tions can be found in spectral graph theory or ma-
chine learning. A popular variant is provided by
the symmetric normalized Laplacian(SNL)(Chung,
1996), capturing the structural relationships of graphs
that are caused by symmetrically normalizing the ad-
jacency matrix. Meanwhile, the random-walk nor-
malized Laplacian(RWL)(Schaub et al., 2020) pro-
vides a probabilistic view; hence, it is possible to
investigate the random-walk dynamics on the graph
nodes. These Laplacian matrices have been funda-
mental in applications such as trajectory analysis and
personalized PageRank, complementing strengths in
interpreting graph-structured data. They form the
mathematical backbone of many graph learning tech-
niques and provide a seamless bridge from traditional
graph analysis to modern neural network methodolo-
gies.
In the domain of recommendation systems, the
integration of GNNs with knowledge graphs opened
new dimensions for improved precision in recommen-
dations. Models like PyRec (Li et al., 2024) incorpo-
rate GNNs along with KGs to effectively model pair-
wise and contextual relations, improving their cap-
ture power for complex user-item interactions. How-
ever, the sensitivity of the GNN performance due to
different normalization schemes applied to the adja-
cency matrix is relatively underexploited. This criti-
cal gap brings out the need to systematically investi-
Towards an Approach for Project-Library Recommendation Based on Graph Normalization
121

gate the influence of various normalization techniques
that might have broad ramifications in the accuracy
and scalability aspects of graph-based recommenda-
tion systems.
3 METHODOLOGY
The proposed framework will investigate the impact
of normalization schemes on GNNs applied to project
library recommendation systems. Analyzing the be-
havior of GNNs in light of different normalization
techniques aims to reveal their role in optimizing fea-
ture propagation and graph representation with re-
spect to recommendation tasks. The following sub-
sections explain these in detail, stating the theoretical
basis and implementing the approach.
3.1 Preliminaries
Graph neural networks (GNNs) operate on graph-
structured data, leveraging relationships between
nodes to propagate and aggregate information(Li
et al., 2018; Wu et al., 2020). To formalize the repre-
sentation of a graph, we consider an undirected graph
G = (V,E), where V is the set of vertices and E is the
set of edges. The adjacency matrix A ∈ R
n×n
and the
degree matrix D ∈ R
n×n
are defined as follows:
A
i j
=
(
1 if (v
i
,v
j
) ∈ E,
0 otherwise,
(1)
D
ii
=
∑
j
A
i j
. (2)
Graph Laplacians are critical in the analysis of
graph structures, commonly used in spectral graph
theory and machine learning for tasks like cluster-
ing and node classification (Chung, 1997; Belkin and
Niyogi, 2003). The Laplacian matrix L encodes the
structural properties of the graph and is defined as:
L = D −A. (3)
Additionally, to accommodate normalization
schemes, two variants of the Laplacian are commonly
employed:
Symmetric Normalized Laplacian (SNL):
L
sym
= I − D
−1/2
AD
−1/2
, (4)
where I is the identity matrix.
Random-Walk Normalized Laplacian (RWL):
L
rw
= I − D
−1
A. (5)
These matrices play a critical role in defining the
propagation rule for graph neural networks (GNNs),
which iteratively update node representations by ag-
gregating information from neighboring nodes. For a
single GNN layer, the propagation rule is:
H
(l+1)
= σ

L
norm
H
(l)
W
(l)

, (6)
where H
(l)
∈ R
n×d
denotes the node features at the l-
th layer, W
(l)
∈ R
d×d
′
is the trainable weight matrix,
σ(·) is a non-linear activation function, and L
norm
can
be substituted with L
sym
or L
rw
depending on the nor-
malization scheme.
In our investigation, these normalized Laplacians
are evaluated for their impact on GNN performance in
the context of project-library recommendation tasks.
By analyzing the performance of models using SNL
and RWL, we aim to discern their influence on the
propagation of node information and overall recom-
mendation accuracy.
3.2 Normalization Schemes on GNNs
Normalization plays a pivotal role in the design and
functionality of Graph Neural Networks (GNNs). It
directly affects how information is propagated across
the graph, ensuring that features from neighboring
nodes are appropriately aggregated without being
dominated by nodes with higher degrees. Two widely
adopted normalization schemes for the adjacency ma-
trix are symmetric normalization and random-walk
normalization. These schemes address the challenges
posed by unbalanced node degrees and ensure effec-
tive learning from the graph structure.
The symmetric normalization scheme is repre-
sented as:
ˆ
A
sym
= D
−1/2
AD
−1/2
where D is the degree matrix and A is the adja-
cency matrix. This normalization method ensures that
the contributions of neighboring nodes are inversely
weighted by their degrees. As a result, it treats all
nodes equitably, preventing over-emphasis on high-
degree nodes. Symmetric normalization is particu-
larly beneficial in tasks where the graph exhibits a
high degree of heterogeneity in its node connectiv-
ity. On the other hand, the random-walk normaliza-
tion scheme is defined as:
ˆ
A
rw
= D
−1
A
This scheme is based on the random-walk dynamics
of the graph, where the transition probability from
a node to its neighbors is inversely proportional to
its degree. Random-walk normalization is especially
useful for modeling diffusion processes and random-
walk-based tasks.
In the context of project-library recommenda-
tion systems, normalization schemes influence how
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
122

Algorithm 1: Procedure for Normalization Impact Analysis (NIA)
1 . Input: Graph G := {A,X} with adjacency matrix A and feature matrix X , normalized Laplacian
matrices
ˆ
A
sym
,
ˆ
A
rw
, GNN model f (H, Θ), parameters λ
1
, λ
2
, learning rate γ, number of epochs N,
sparsity thresholds τ
sym
,τ
rw
.
Output: Optimized GNN and evaluation metrics.
2 Initialize: Set initial weights and adjacency matrices.
3 for i = 0 to N − 1 do
4 Forward Pass: Compute node representations:
5 H
(l+1)
sym
= σ(
ˆ
A
sym
H
(l)
W
(l)
); //Update project embeddings
6 H
(l+1)
rw
= σ(
ˆ
A
rw
H
(l)
W
(l)
); //Update TPL embeddings
7 Compute the loss function:
8 L = L
GNN
(H
sym
,H
rw
,Y ) +λ
1
∥W ∥
2
+ λ
2
∥A∥
1
; //Loss function calculation
9 Backward Pass: Update GNN weights:
10 W
(l+1)
← W
(l)
− γ∇
W
(l)
L; //Gradient descent update for weights
11 Update adjacency matrices:
12
ˆ
A
sym
←
ˆ
A
sym
− γ∇
ˆ
A
sym
L; //Update symmetric adjacency matrix
13
ˆ
A
rw
←
ˆ
A
rw
− γ∇
ˆ
A
rw
L; //Update random-walk adjacency matrix
14 Pruning: Set τ
sym
values in
ˆ
A
sym
to 0, and others to 1; //Apply sparsity threshold for
ˆ
A
sym
15 Set τ
rw
values in
ˆ
A
rw
to 0, and others to 1; //Apply sparsity threshold for
ˆ
A
rw
16 Re-training: Retrain the GNN with pruned adjacency matrices; //Refine the model on pruned graph
structure
17 Evaluation: Measure performance metrics such as precision, recall, and F1-score; //Evaluate final
model performance
project and library features are propagated through
the graph. The symmetric normalization scheme em-
phasizes structural regularity by balancing node de-
grees, making it well suited for graphs with diverse
connectivity patterns. Meanwhile, random-walk nor-
malization better captures sequential or flow-based
dynamics, which may be significant in contexts where
the relationship between projects and libraries follows
a temporal or directional pattern.
The propagation mechanism in GNN can be sum-
marized as:
H
l+1
= σ(
ˆ
AHlW l)
where
ˆ
A can be
ˆ
A
sym
or
ˆ
A
rw
, H
l
is the node fea-
ture matrix at layer l, W
l
is the trainable weight ma-
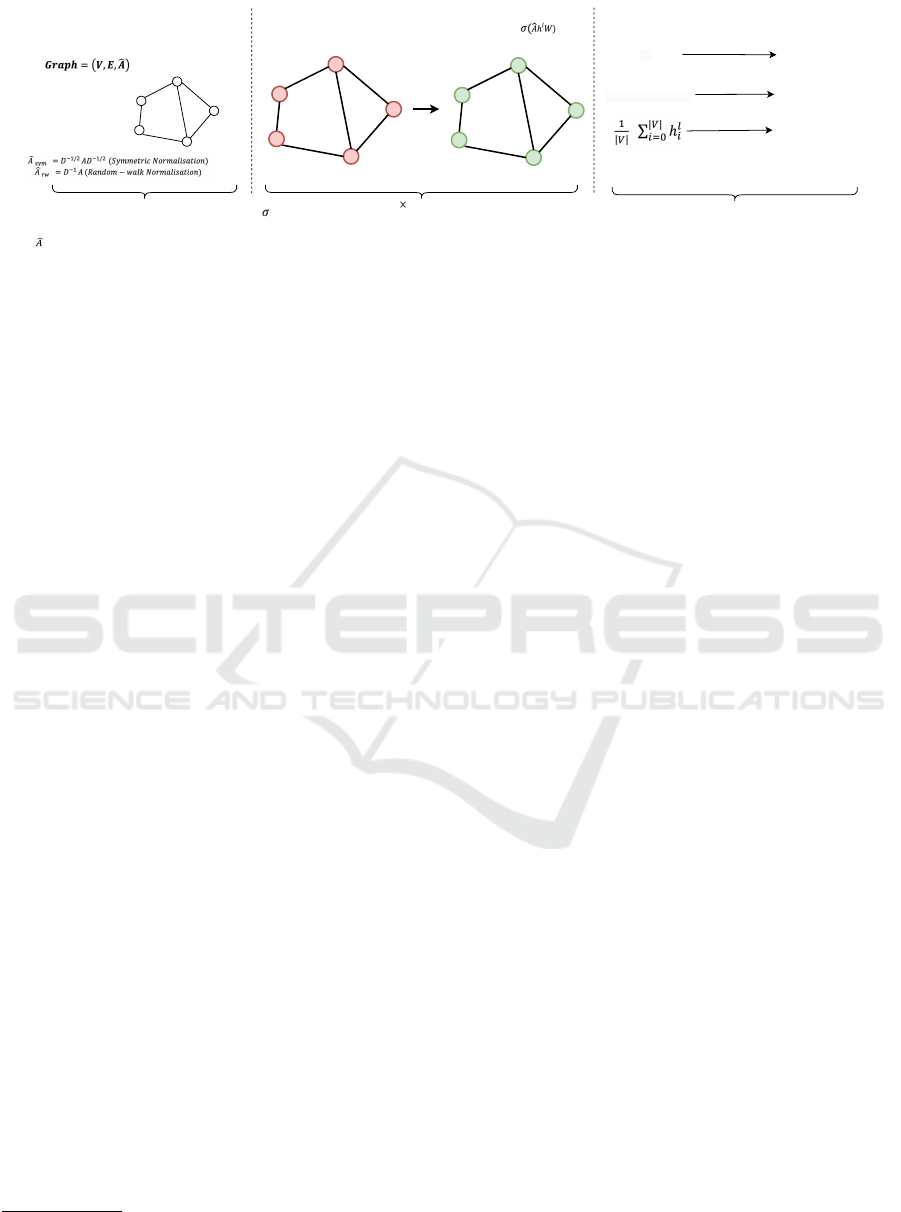
trix, and σ is the activation function. As illustrated
in Figure 1, the node features (h) and the edge fea-
tures (e) are processed through successive layers of
GNN, with the information iteratively propagated and
updated. The features of the nodes h
l
i
obtained after
propagation are utilized for prediction tasks.
1
|V |
|V |
∑
i=0
h
l
i
where |V | is the total number of nodes in the graph
and h
l
i
is the embedding of node i at layer l. This
process ensures that the global graph representation
is captured, enabling effective predictions at the graph
level.
To assess the impact of these normalization
schemes, the study follows the workflow described
in Algorithm 1. This algorithm outlines the itera-
tive process of updating node embeddings and adja-
cency matrices, ensuring consistency in the evaluation
of the two normalization approaches. Figure1 com-
plements this by providing a graphical representa-
tion of the GNN architecture, including the input fea-
tures, feature propagation, and prediction layers. To-
gether, these elements provide a comprehensive view
of how normalization schemes affect GNN perfor-
mance. By systematically analyzing the performance
of these normalization schemes in the project-library
dataset, this work highlights their strengths and weak-
nesses and provides actionable insights for selecting
an appropriate scheme based on the characteristics of
the graph.
Towards an Approach for Project-Library Recommendation Based on Graph Normalization
123

Input Layer
Node features : h
Edge Feature : e
V - Represents the nodes
E - Represents the Edges
- Represents the normalised adjacency matrix
L * GNN Layer Prediction Layer
h4
h0
h2
h3
h1
GNN
l
Layer l : h
l
Layer l+1 :
MLP
h4
h0
h2
h3
h1
W - Trainable Weight matrix
h
l
- Node Feature at layer l
- Non Linear Activation function
e
04
e
01
e
12
e
24
e
23
e
34
e
34
e
04
e
23
e
24
e
12
e
01
h
i
l
Node Predictions
MLP
Concat (h
i
l
+h
j
l
)
Edge Predictions
MLP
Graph Predictions
Figure 1: GNN architecture illustrating input features, feature propagation through GNN layers, and node, edge, and graph-
level predictions.
4 EXPERIMENTAL SETUP AND
RESULTS
This section details the experimental setup used to
evaluate the applied framework, followed by the re-
sults obtained. The evaluation is based on the project
library dataset.
4.1 Dataset
The study uses a large-scale heterogeneous data set
specifically designed for the recommendation of the
third-party library (TPL). It includes 12,421 Python
projects, 963 distinct TPLs, 9,675 additional enti-
ties, 121,474 project-library interaction records, and
73,277 pieces of contextual information. The nodes
represent projects, libraries, and entities, while the
edges capture relationships such as library usage.
The data set supports advanced graph-based meth-
ods, and its scale (13,000+ nodes and 200,000+
edges) ensures evaluation under realistic conditions.
It is publicly available for validation and reproduc-
tion of results
1
. In this study, the same data splits as
(Li et al., 2024) are applied.
4.2 Network Settings
Figure 1 illustrates the architecture of the GNN model
used in this study. The input layer incorporates
node and edge features along with the normalized ad-
jacency matrix, supporting symmetric and random-
walk normalization schemes. The GNN layer prop-
agates features through multiple layers, using non-
linear activation functions and trainable weight ma-
trices. Finally, the prediction layer enables predic-
tions at the node, edge, and graph levels, effectively
1
https://github.com/Limber0117/PyRec/tree/main/
datasets
aligning with the requirements of project-library rec-
ommendation tasks.
The backbone network is trained for up to 1000
epochs using the Adam optimizer with a learning rate
of 0.0001. The model uses node embeddings and re-
lation embeddings of dimensions 128 and 64, respec-
tively. Two aggregation layers, each with an output
dimension of 64, are employed with a bi-interaction
mechanism. A message dropout rate of 1% is uni-
formly applied across layers to enhance regulariza-
tion. The adjacency matrix (Laplacian) supports two
normalization schemes: symmetric and random walk,
which can be specified as part of the configuration.
The training process includes an early stoppage if no
improvement in recall is observed in 15 consecutive
epochs. Recommendations are evaluated based on
metrics calculated at K = [5,10,20], ensuring robust
performance analysis. This configuration provides a
flexible framework for effective project-library rec-
ommendation tasks.
4.3 Result Analysis
This study evaluates the impact of four normalization
techniques: symmetric normalized Laplacian (SNL),
random walk normalized Laplacian (RWN), double
stochastic normalization (DSN) and unnormalized
Laplacian (UNL) on the library recommendation task.
The evaluation was carried out on datasets with vary-
ing levels of missing library information (rm = 20%,
rm = 40%, and rm = 60%), using metrics such as
mean precision (MP), mean recall (MR), mean F1
score (MF), mean reciprocal rank (MRR) and mean
average precision (MAP) at K = 5,10, 20. The results
are summarized in Table 1.
The main focus of the paper is on SNL and RWN,
as these techniques are emphasized throughout the ap-
plied framework. However, DSN and UNL were in-
cluded purely for comparative purposes to serve as
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
124

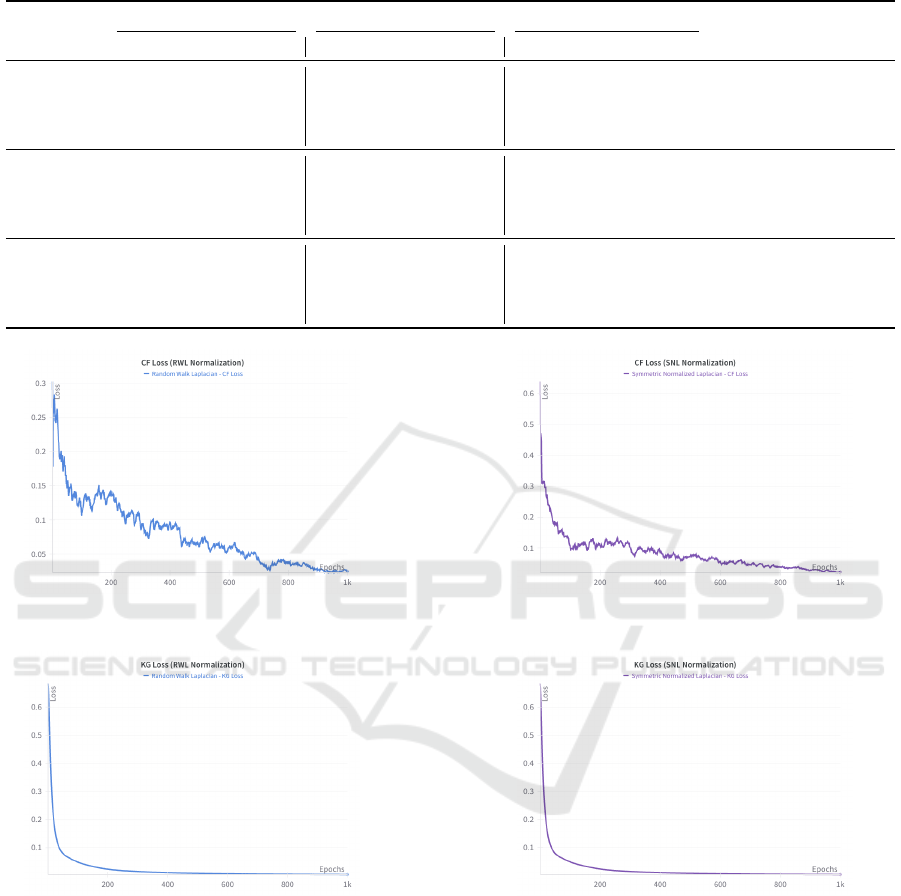
Table 1: Performance Comparison of Different Normalization Techniques.
Dataset Norm K = 5 K = 10 K = 20
MP MR MF MRR MAP MP MR MF MRR MAP MP MR MF MRR MAP
rm=20%
UNL 0.105 0.366 0.169 0.306 0.254 0.066 0.490 0.122 0.344 0.280 0.045 0.572 0.088 0.355 0.287
DSN 0.112 0.373 0.169 0.313 0.258 0.079 0.488 0.128 0.340 0.377 0.049 0.584 0.092 0.349 0.273
SNL 0.121 0.378 0.171 0.327 0.261
0.072 0.484 0.125 0.342 0.283 0.051 0.592 0.107 0.359 0.295
RWN 0.123 0.424 0.191 0.375 0.299 0.080 0.535 0.139 0.390 0.314 0.060 0.640 0.109 0.396 0.323
rm=40%
UNL 0.201 0.303 0.251 0.507 0.257 0.130 0.429 0.214 0.489 0.274 0.104 0.489 0.138 0.514 0.284
DSN 0.205 0.315 0.254 0.502 0.265 0.131 0.418 0.212 0.502 0.270 0.110 0.491 0.141 0.528 0.280
SNL 0.211 0.342 0.261 0.517 0.264 0.143 0.454 0.218 0.531 0.281 0.112 0.548 0.159 0.536 0.288
RWN 0.227 0.366 0.280 0.551 0.285 0.152 0.479 0.231 0.564 0.300 0.183 0.557 0.194 0.567 0.310
rm=60%
UNL 0.274 0.295 0.284 0.504 0.249 0.197 0.411 0.266 0.503 0.257 0.156 0.250 0.216 0.413 0.267
DSN 0.285 0.305 0.294 0.572 0.263 0.201 0.418 0.272 0.519 0.270 0.160 0.257 0.211 0.428 0.280
SNL 0.286 0.306 0.295 0.612 0.264 0.201 0.419 0.272 0.622 0.260 0.132 0.261 0.211 0.625 0.281
RWN 0.288 0.309 0.298 0.621 0.271 0.203 0.421 0.274 0.611 0.275 0.160 0.291 0.242 0.634 0.292
(a) CF Loss curve for RWL. (b) CF Loss curve for SNL.
(c) KG Loss curve for RWL. (d) KG Loss curve for SNL.
Figure 2: Loss curves for Collaborative Filtering(CF) and Knowledge Graph (KG) under Symmetric Normalized Laplacian
(SNL) and Random Walk Laplacian (RWL) normalization schemes.
benchmarks, highlighting the strengths of SNL and
RWN. The inclusion of DSN and UNL is justified by
their widespread use in graph-based learning tasks,
offering a broader perspective on performance.
For rm = 20%, SNL achieved an MF of 0.191 at
K = 5, demonstrating its stability for smaller values
K. However, it was outperformed by RWN in all met-
rics. For example, RWN achieved an MF of 0.280 at
K = 5 and an MAP of 0.299, compared to 0.261 for
SNL. DSN and UNL also performed reasonably well,
and UNL achieved an MF of 0.169 at K = 5, indicat-
ing its limitations in quality classification compared
to the other techniques.
As the level of missing data increased to rm =
40%, RWN demonstrated its robustness with an MF
of 0.280 at K = 5, significantly outperforming SNL,
which achieved an MF of 0.264. Both DSN and
UNL lagged behind, and DSN showed better MAP
Towards an Approach for Project-Library Recommendation Based on Graph Normalization
125

and MRR values compared to UNL, particularly at
higher values K. RWN’s ability to maintain superior
MAP and MRR scores highlights its capacity to han-
dle sparse and incomplete datasets effectively.
For rm = 60%, RWN continued to outperform
other normalization schemes, achieving an MF of
0.298 at K = 5 and an MAP of 0.292 at K = 20.
SNL achieved an MF of 0.264 and an MAP of 0.281
at K = 20, showing its limitations in sparse scenar-
ios. DSN and UNL exhibited declining performance
as sparsity increased, strengthening the robustness of
RWN in high-sparsity environments.
The loss curves presented in Figure 2 further
validate these findings. The Collaborative Filtering
(CF) and Knowledge Graph (KG) loss curves indicate
faster convergence and stability for RWN compared
to SNL. Specifically, RWN achieved lower overall CF
and KG losses, reflecting its ability to learn more ef-
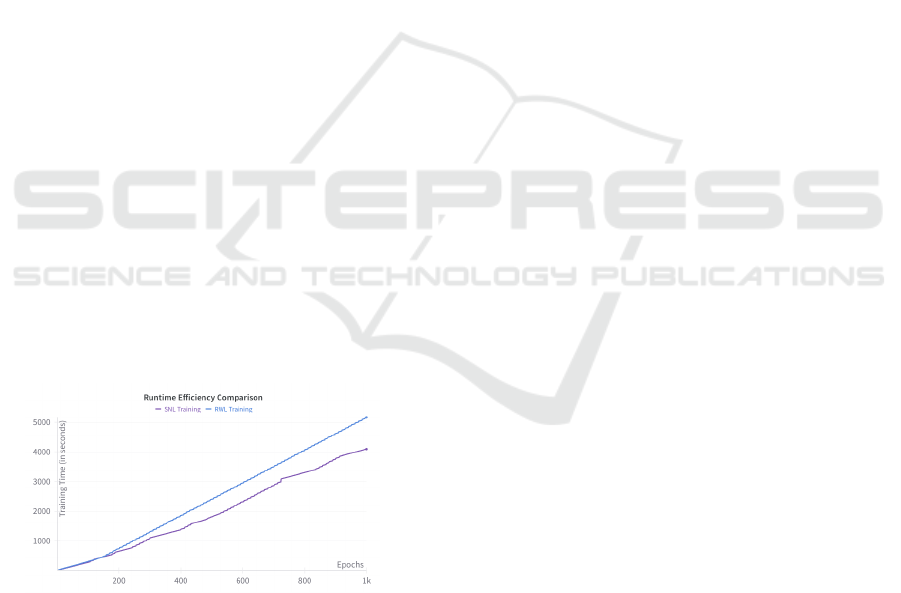
fectively. Figure 3 compares the runtime efficiency
of SNL and RWN, showing that while RWN required
slightly more computation time, its superior perfor-
mance justifies the trade-off.
In general, the results emphasize the superiority
of Random Walk Normalized Laplacian (RWN) over
Symmetric Normalized Laplacian (SNL) for the li-
brary recommendation task. Although DSN and UNL
provided additional information, their inclusion was
purely for comparative purposes. The ability of RWN
to capture higher-order interactions and deliver supe-
rior ranking performance makes it a preferred choice,
particularly in sparse settings. These findings validate
the design choices of the applied framework and high-
light the critical role of normalization schemes in en-
hancing the quality of recommendations and retrieval
performance.
Figure 3: Runtime Efficiency Comparison between SNL
and RWL.
5 CONCLUSIONS
This study evaluated the impact of the Symmetric
Normalized Laplacian (SNL) and the Random Walk
Normalized Laplacian (RWN) on the performance of
the PyRec recommendation model in data sets with
varying levels of missing library information (rm =
20%, 40%, 60%). The results show that RWN consis-
tently outperforms SNL in all sparsity levels and eval-
uation metrics, particularly in sparse scenarios (rm =
60%), highlighting its robustness and ability to im-
prove ranking quality. Although SNL performs rea-
sonably well on dense datasets (rm = 20%), its effec-
tiveness diminishes with increasing sparsity.
Future work will explore additional normalization
techniques, such as Doubly Stochastic Normaliza-
tion and Unnormalized Laplacian, to further improve
the adaptability of PyRec. Investigating the interac-
tion between normalization schemes, hyperparameter
configurations, and temporal dynamics will also be
prioritized to improve the scalability and generaliz-
ability of the model.
These findings emphasize the critical role of nor-
malization techniques in improving the performance
of graph-based recommendation systems and open
avenues for further advancements in handling sparse
and complex data sets.
REFERENCES
Asif, N. A., Sarker, Y., Chakrabortty, R. K., Ryan, M. J.,
Ahamed, M. H., Saha, D. K., Badal, F. R., Das, S. K.,
Ali, M. F., Moyeen, S. I., et al. (2021). Graph neural
network: A comprehensive review on non-euclidean
space. Ieee Access, 9:60588–60606.
Belkin, M. and Niyogi, P. (2003). Laplacian eigenmaps
for dimensionality reduction and data representation.
Neural computation, 15(6):1373–1396.
Chung, F. R. (1996). Lectures on spectral graph theory.
CBMS Lectures, Fresno, 6(92):17–21.
Chung, F. R. (1997). Spectral graph theory, volume 92.
American Mathematical Soc.
Isinkaye, F. O., Folajimi, Y. O., and Ojokoh, B. A. (2015).
Recommendation systems: Principles, methods and
evaluation. Egyptian informatics journal, 16(3):261–
273.
Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-
sification with graph convolutional networks. arXiv
preprint arXiv:1609.02907.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Li, B., Quan, H., Wang, J., Liu, P., Cai, H., Miao, Y., Yang,
Y., and Li, L. (2024). Neural library recommendation
by embedding project-library knowledge graph. IEEE
Transactions on Software Engineering.
Li, Q., Han, Z., and Wu, X.-M. (2018). Deeper in-
sights into graph convolutional networks for semi-
supervised learning. In Proceedings of the AAAI con-
ference on artificial intelligence, volume 32.
ENASE 2025 - 20th International Conference on Evaluation of Novel Approaches to Software Engineering
126

Mastropietro, A., Pasculli, G., and Bajorath, J. (2023).
Learning characteristics of graph neural networks pre-
dicting protein–ligand affinities. Nature Machine In-
telligence, 5(12):1427–1436.
Puny, O., Ben-Hamu, H., and Lipman, Y. (2020). From
graph low-rank global attention to 2-fwl approxima-
tion. arXiv preprint arXiv:2006.07846.
Schaub, M. T., Benson, A. R., Horn, P., Lippner, G., and
Jadbabaie, A. (2020). Random walks on simpli-
cial complexes and the normalized hodge 1-laplacian.
SIAM Review, 62(2):353–391.
Veli
ˇ
ckovi
´
c, P., Cucurull, G., Casanova, A., Romero, A., Lio,
P., and Bengio, Y. (2017). Graph attention networks.
arXiv preprint arXiv:1710.10903.
Wu, L., Ying, X., and Wu, X. (2010). Reconstruction from
randomized graph via low rank approximation. In
Proceedings of the 2010 SIAM International Confer-
ence on Data Mining, pages 60–71. SIAM.
Wu, S., Sun, F., Zhang, W., Xie, X., and Cui, B. (2022).
Graph neural networks in recommender systems: a
survey. ACM Computing Surveys, 55(5):1–37.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Philip,
S. Y. (2020). A comprehensive survey on graph neural
networks. IEEE transactions on neural networks and
learning systems, 32(1):4–24.
Xu, K., Hu, W., Leskovec, J., and Jegelka, S. (2018). How
powerful are graph neural networks? arXiv preprint
arXiv:1810.00826.
Yang, L., Shi, R., Zhang, Q., Wang, Z., Cao, X., Wang, C.,
et al. (2024). Self-supervised graph neural networks
via low-rank decomposition. Advances in Neural In-
formation Processing Systems, 36.
Ye, Y., Xiao, Y., Zhou, Y., Li, S., Zang, Y., and Zhang,
Y. (2023). Dynamic multi-graph neural network for
traffic flow prediction incorporating traffic accidents.
Expert Systems with Applications, 234:121101.
Zhang, D., Yin, J., Zhu, X., and Zhang, C. (2018). Network
representation learning: A survey. IEEE transactions
on Big Data, 6(1):3–28.
Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z.,
Wang, L., Li, C., and Sun, M. (2020). Graph neu-
ral networks: A review of methods and applications.
AI open, 1:57–81.
Towards an Approach for Project-Library Recommendation Based on Graph Normalization
127