Graph-Based Learning for Multimodal Route Recommendation

Zakariya Ghalmane

and Brahim Daoud

CESI LINEACT UR 7527, Strasbourg, France

Keywords:

Graph Convolutional Network, Complex Networks, Centrality Measures, Multi-Task Learning, Multimodal

Transportation, Route Recommendation.

Abstract:

Transportation recommendations are a vital feature of map services in navigation applications. Earlier trans-

portation recommendation systems have struggled to deliver a satisfactory user experience because they focus

exclusively on single-mode routes, such as cycling, taxis, or buses. In this paper, we represent the transporta-

tion network as a complex network (or graph). Modeling transportation as a network of nodes and edges has

gained attention in the literature, generating numerous studies over the years. This approach requires a clear

deﬁnition of what constitutes a node or an edge: nodes represent stops, while edges represent road segments

connecting these stops. Based on this representation, we propose a framework that generates embeddings for

each node and edge in the transportation network. These embeddings are created using GRU (Gated Recurrent

Units) and GCN (Graph Convolutional Network) models to capture spatial and temporal patterns within the

network, while incorporating centrality measures reﬂecting the inﬂuence of each stop. This vector represen-

tation facilitates multi-task learning for effective multi-modal transportation recommendations. The proposed

framework is applied to the transportation network of Strasbourg, France. Experimental results demonstrate

the framework’s efﬁciency in recommending suitable multimodal transportation routes, considering criteria

such as meteorological conditions, safety, and passenger comfort.

1 INTRODUCTION

The growing prevalence of diverse modes of trans-

portation (such as buses, cars, bike-sharing, carpool-

ing, . . . ) and the rapid expansion of transportation

networks (like bus, pedestrian or road networks, . . . .)

have offered travelers with a multitude of options to

reach their destinations. Over the past few years,

transport recommendation has emerged as a valu-

able routing service within various navigation and

carpooling applications, such as Here, Didi Chuxing

and Baidu Maps. The goal of transport recommen-

dation is to assist users in ﬁnding the most suitable

route from one location to another.As a result, pre-

cise and intelligent transport recommendations can al-

low to signiﬁcantly help reduce travelers’ decision-

making costs and ultimately enhance the user experi-

ence (Song et al., 2018).

Recently, researchers devoted considerable atten-

tion to route recommendation because of its essential

component in mapping services (Wei et al., 2012).

The quality of route recommendations has been im-

proved by leveraging massive historical datasets (such

https://orcid.org/0000-0002-2440-2886

as mobile registration data (Shaﬁque and Ali, 2016),

and GPS trajectory data (Yuan et al., 2010)) with

the widespread use of mobile devices and location-

based services. Existing studies on transport mode

recommendation can be grouped into three main cat-

egories. The ﬁrst category focuses on ﬁnding the

shortest path within the transport network, based on a

predeﬁned distance metric (e.g., geographic distance,

travel time). Most methods in this category extend

graph search algorithms to transport networks (e.g.,

Dijkstra, Bellman–Ford, and contraction hierarchies)

(Candra et al., 2020; Iqbal et al., 2018; Geisberger

et al., 2012). However, these approaches rely heav-

ily on a predeﬁned metric like the distance and of-

ten overlook latent factors in the data such us mode

and route preferences in different situational con-

texts (Liu et al., 2019). The second category par-

tially addresses this limitation by inferring transport

mode preferences using supervised or unsupervised

machine learning techniques. A common approach

in such methods is to explicitly extract features (dis-

tance, estimated time of arrival (ETA)) from historical

user data, such as GPS trajectories and in-app clicks.

These methods make recommendations based on em-

Ghalmane, Z. and Daoud, B.

Graph-Based Learning for Multimodal Route Recommendation.

DOI: 10.5220/0013356300003944

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Internet of Things, Big Data and Security (IoTBDS 2025), pages 313-320

ISBN: 978-989-758-750-4; ISSN: 2184-4976

313

pirically deﬁned features, which heavily depend on

the completeness of feature engineering. More re-

cent studies have applied deep learning to transport

mode recommendation (Chen et al., 2020; Liu and

Jiang, 2022; Hopman et al., 2021). The third category

uses graph-based learning, extending Graph Neu-

ral Networks (GNNs), which are well-suited to cap-

ture spatial dependencies in graph structures (Sharma

et al., 2023; Hamilton et al., 2017; Jiang and Luo,

2022; Kipf and Welling, 2016; da Silva et al., 2023;

MOEZZI, ; Jana et al., 2023). Recently, graph-based

learning has been widely applied to many spatiotem-

poral exploration tasks, such as ﬂow prediction and

parking availability prediction (Wang et al., 2019).

However, none of the aforementioned studies speciﬁ-

cally address multimodal transport recommendations.

In this context, the objective of this work is to

model the multimodal transportation network using

a graph or a complex network approach. Complex

network (graph) modelization is essential for uncov-

ering hidden patterns in interconnected systems, with

applications spanning diverse domains such as biol-

ogy, social sciences, technology, and transportation

(Ding et al., 2019; Termos et al., 2024; Termos et al.,

2023; Latora et al., 2017; GHALMANE et al., 2023;

Shanmukhappa et al., 2019; Zanin and Lillo, 2013;

Ghalmane et al., 2020; Ghalmane et al., 2021; Ghal-

mane et al., 2022). To achieve this, we discretize

the multimodal transportation network into a series

of graph snapshots over time and construct a tempo-

ral graph, where each node represents a bus, metro,

tram, or bike-sharing station, and each link repre-

sents a bus/metro/tram line or road segment. This

model provides critical structural insights into the

transportation network. Based on this model, we

propose a framework comprising two main compo-

nents: a prediction module and a recommendation

module. The prediction module includes a spatiotem-

poral GNN-based model, which features a GRU layer

for capturing temporal autocorrelations across mul-

tiple graph snapshots, and a GNN layer for captur-

ing non-linear spatial autocorrelations from the trans-

portation network graph. These representation-based

models excel in capturing relationships and patterns

in graph-structured data, making them highly suitable

for transportation network modeling. In this repre-

sentation, the centrality measures (Ghalmane et al.,

2019; Ghalmane et al., 2018a) are also added to the

embedding of each node (stop) quantifying its impor-

tance in the transportation network. The prediction

module enables the forecasting of parameters for each

itinerary, such as route distance, travel duration, CO2

emission, confort and safety. These predicted param-

eters are then used to classify different itineraries, fa-

cilitating the recommendation of the best multimodal

itinerary. The recommendation process relies on an

objective function that aligns with multiple goals, in-

cluding minimizing carbon emissions, reducing travel

time, and enhancing safety and comfort. This pro-

posed framework was applied to the transportation

network of Strasbourg, France, to assist students in

navigating from their homes to their campuses. Re-

sults demonstrate that the framework accurately rec-

ommends the best multimodal itineraries for students

in Strasbourg. Furthermore, the proposed framework

can be generalized to other cities with different trans-

portation infrastructures. In this paper, we focus on

Strasbourg due to the availability of transportation

data for the city.

The remainder of this paper is organized as fol-

lows: Section 2 outlines the methodology, detailing

the graph construction, feature selection, and integra-

tion of complex network measures with the GNN and

GRU models. Section 3 presents the experimental re-

sults on Strasbourg’s transportation network data. Fi-

nally, Section 5 summarizes the contributions of the

methodology and concludes the study.

2 MATERIALS AND METHODS

In this section, we begin by providing an overview

of the proposed approach, followed by a detailed de-

scription of each step in the subsequent subsections.

2.1 General Scheme

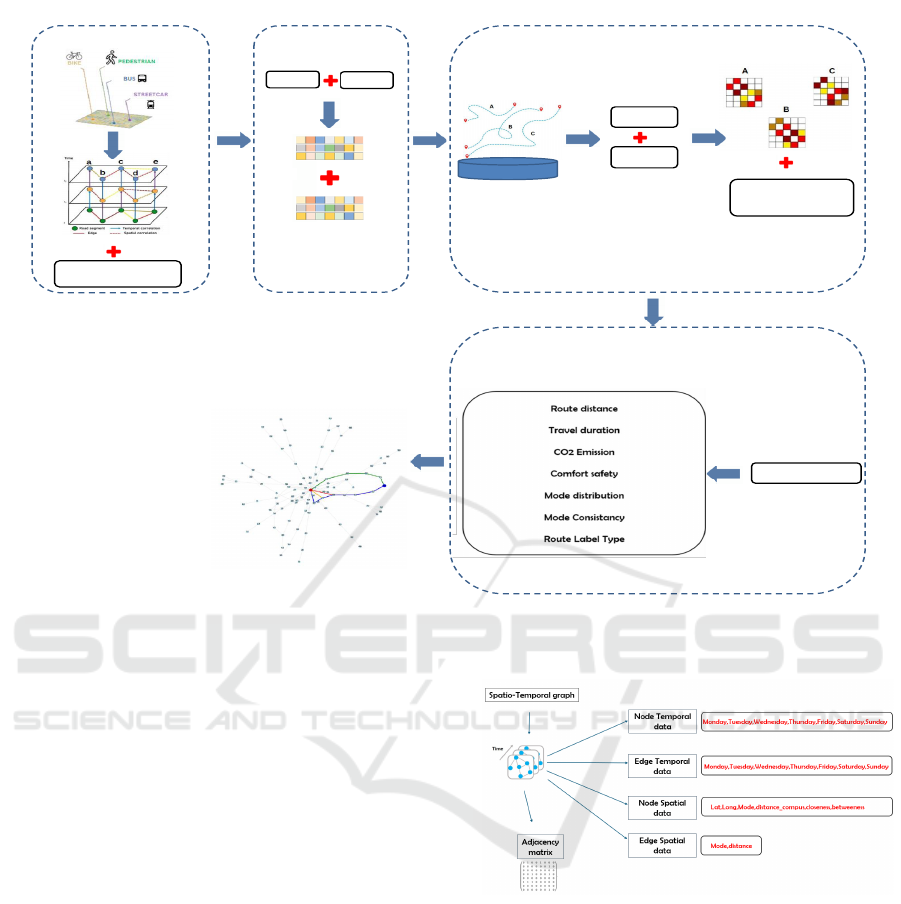
Here, we provide an overview of the proposed

methodology, as illustrated in Figure 1. First, a com-

plex network (or graph) is constructed based on trans-

portation data. This graph is inherently temporal,

reﬂecting the dynamic nature of transportation net-

works. Each node and edge in the graph is asso-

ciated with a set of features, including two central-

ity measures: Betweenness and Closeness (Ghalmane

et al., 2019; Ghalmane et al., 2018a; Ghalmane et al.,

2018b). These centrality measures offer insights into

the relative importance of nodes (stops) in connecting

different routes and regions within the transportation

network. Once the graph is constructed with these

enriched node and edge features, the prediction and

recommendation modules are applied. The ﬁrst com-

ponent of the prediction module involves two mod-

els: GRU (Gated Recurrent Units) and GCN (Graph

Convolutional Network). These models generate em-

beddings for each node and edge, capturing the spa-

tial and temporal patterns within the network. Sub-

sequently, the overall embedding of a given route is

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

314

Multi-modal transportation

recommendation

GCN

GRU

Historical data

BiGRU

Attention

One Hot Encoded

Context

Temporal multimodal graph creation

Node and edge embedding

Route sequences learning

Multi-task learning

Neural Network

Centrality measures

Figure 1: General scheme of the proposed framework.

computed using a BiGRU model, leveraging the em-

beddings of the sequence of nodes and edges that con-

stitute the input route. In the second component of

the prediction module, these route embeddings are

combined with contextual data—such as safety, com-

fort, and meteorological conditions—and are fed into

a multi-layer neural network. This network performs

multiple regression and classiﬁcation tasks to predict

various parameters for each route, including route dis-

tance, travel duration, CO2 emissions, comfort level,

safety, mode consistency, and route type. Finally,

the recommendation module ranks the different routes

based on these predicted parameters. This ranking is

achieved using an objective function.

2.2 Temporal Multimodal Graph

Creation

The transportation network is modeled as a multi-

modal graph representing bus, tram, and bike-sharing

systems, with nodes for stations and edges for con-

nections. Data from General Transit Feed Speciﬁca-

tion (GTFS) and General Bikeshare Feed Speciﬁca-

tion (GBFS) ﬁles is used to create the graph, link-

ing bus/tram stops and bike stations based on prox-

Figure 2: The spatial, temporal and network features of the

multimodal network.

imity and transfer points. Each node and edge is

enriched with spatial and temporal features, such as

geographic coordinates, centrality measures (close-

ness and betweenness), and estimated daily passen-

ger ﬂow. Temporal data is added to capture network

dynamics, including passenger counts and route ca-

pacities throughout the day. This multimodal network

helps optimize travel routes and analyze urban trans-

portation patterns, considering both static and time-

dependent network changes.

Graph-Based Learning for Multimodal Route Recommendation

315

2.3 Node and Edge Embedding

2.3.1 Temporal Embedding

The temporal pattern of the multimodal network is

captured by using Gated Recurrent Unit (GRU) model

(Yu et al., 2019). The output of the GRU layer is a

temporal embedding for each node and edge. This

embedding condenses the temporal patterns captured

over the week into a lower-dimensional space, allow-

ing the model to focus on the most relevant temporal

dynamics for subsequent learning tasks. The tempo-

ral data is processed by a GRU, a common sequence

modeling layer. The GRU is conﬁgured with:

- Input Shape: 7, representing the number of days

in the week as temporal features.

- Output Shape: 3, indicating that the GRU re-

duces the temporal data into a 3-dimensional em-

bedding for each node.

- Number of Hidden Units: 32, which deﬁnes the

number of neurons in the hidden layers of the

GRU, controlling the capacity to capture tempo-

ral dependencies.

- Recurrent Dropout: 0.15, applying dropout to

prevent overﬁtting during the learning process.

- Number of Layers: 2, meaning that the GRU has

two layers to ensure deeper processing of sequen-

tial information.

- Activation Function: ReLU, which introduces

non-linearity in the model and helps in capturing

complex temporal interactions.

Following the generation of the temporal embedding

for nodes and edges, the temporal information is

concatenated with spatial features. The spatial

information complements the temporal embedding,

allowing the model to integrate both spatial and

temporal correlations. This combination is critical

for understanding how transportation modes and dis-

tances vary over time in the multimodal network. It is

illustrated in Figure 3 for temporal nodes embedding

(the same process is applied to edges).

2.3.2 Spatio-Temporal Embedding

In this section, we observe that the input to the GCN

(Zhang et al., 2019) consists of both node and edge

embeddings, which capture the spatial and temporal

properties of the graph. The concatenation of spatial

and temporal embeddings for both nodes and edges

provides a comprehensive representation of the trans-

portation network. Additionally, the adjacency matrix

Figure 3: Temporal node embedding.

Figure 4: Spatio-temporal correlation.

is included to encode the graph’s structure, describ-

ing the relationships between nodes (i.e., the connec-

tivity of the network). The GCN processes the input

embeddings over multiple layers to produce reﬁned

representations. The conﬁguration of the GCN is as

follows:

- Number of Layers: 3, providing the network

with the depth to capture higher-order neighbor-

hood information in the graph.

- Dropout Rate: 2, to prevent overﬁtting and en-

sure robust generalization during training.

- Activation Function: Leaky ReLU, which in-

troduces non-linearity while allowing for a small

gradient when the unit is not active.

- Initialization: Kaiming initializer, used for

weight initialization to ensure faster convergence

and prevent vanishing gradients, particularly in

deeper layers.

As depicted in Figure 4, the graph convolution

operation is applied iteratively across hidden layers.

At each layer, the GCN aggregates information from

neighboring nodes and edges, thus reﬁning the node

and edge embeddings. The ReLU activation func-

tion is used after each convolution to introduce non-

linearity and capture more complex relationships in

the data. The ﬁnal output of the GCN is a set of re-

ﬁned embeddings for both nodes and edges. These

embeddings are used for downstream tasks, such as

prediction or classiﬁcation. The node embeddings

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

316

Figure 5: Route sequence learning.

capture the latent spatial and temporal features of

each location (bus/tram/bike stop), while the edge em-

beddings encode the dynamic relationships between

connected locations. The embeddings are represented

as multidimensional vectors, as illustrated in the out-

put boxes.

2.4 Route Sequences and Multi-Task

Learning

In this step, the historical routes, consisting of both

nodes and edges, are transformed into their corre-

sponding spatial and temporal embeddings. They are,

then, input into a BiGRU model to obtain an over-

all embedding for each route. These route embed-

dings as well as the contextual data (such as time du-

ration, meteorological conditions, safety and comfort

level) are fed into a neural network model designed

to predict various route-related metrics as illustrated

in Figure 5. This neural network, depicted as a fully

connected layer in the diagram, takes the input em-

beddings and processes them through several hidden

layers, resulting in a set of predictions related to the

routes. The output of the model consists of several

key metrics related to the routes. These include:

- Route Distance: The predicted distance for the

route.

- Travel Duration: The estimated time required to

travel along the route.

- CO2 Emission: An estimate of the carbon diox-

ide emissions for the route, based on the trans-

portation mode and other factors.

- Comfort Safety: A metric that evaluates the com-

fort and safety of the route.

- Mode Distribution: The distribution of trans-

portation modes used in the route.

- Mode Consistency: A measure of how con-

sistently the same transportation mode is used

throughout the route.

- Route Label Type: A classiﬁcation of the route,

such as whether it is a high-speed or scenic route.

This route prediction model described in Figure 1

enables the system to predict multiple key attributes

of a route based on the node and edge embeddings.

By considering both spatial and temporal features,

the model is able to provide accurate and compre-

hensive predictions that are useful for various appli-

cations such as route optimization, environmental im-

pact assessment, and safety evaluations.

2.5 Recommendation System

The route recommendation system utilizes the pre-

dicted parameters of the routes from the historical

dataset to rank and suggest the best itinerary for pas-

sengers traveling from a given starting point. This

recommendation is based on a weighted linear func-

tion that prioritizes CO2 emissions, safety, and dis-

tance. While other parameters such as travel dura-

tion, mode distribution, mode consistency, and route

type are primarily used for training the models within

our framework, they can be integrated into the multi-

objective function if necessary. The function is de-

ﬁned as follows:

f (e, s, d) = α · e + β · s + γ · d (1)

Here, e, s, and d represent the predicted values for

CO2 emissions, safety, and distance of a given route,

respectively. The coefﬁcients α, β, and γ are set to 0.5,

0.3, and 0.2, respectively, to assign greater importance

to CO2 emissions, aligning with the primary goal of

this study to promote low-carbon itineraries.

The recommendation system integrates multiple

factors, including route characteristics, environmen-

tal context, and user preferences, to provide person-

alized route suggestions. This ensures that the rec-

ommended routes reﬂect both objective metrics (e.g.,

distance) and subjective preferences (e.g., safety and

emission reduction). The proposed multimodal route

recommendation system offers passengers a compre-

hensive framework for making well-informed deci-

sions.

3 RESULTS

This section presents the results of training our mul-

timodal route recommendation model, tested in the

city of Strasbourg, France. The model aims to rec-

ommend optimal multimodal itineraries for students

commuting to their campus while minimizing CO2

emissions. We trained the model using historical data,

which includes four potential paths from each node in

Graph-Based Learning for Multimodal Route Recommendation

317

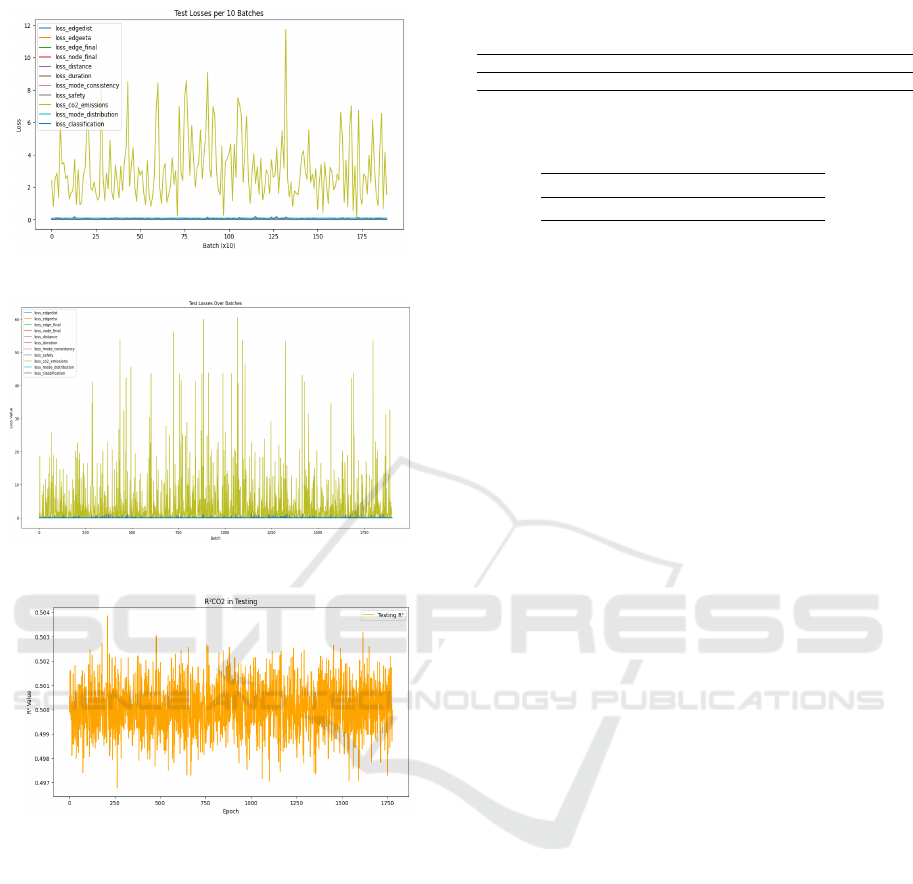
Figure 6: Loss with attention mechanism in test dataset.

Figure 7: Loss without attention mechanism in test dataset.

Figure 8: R2 CO2 in test dataset.

the network to the campus in Strasbourg. The input to

our multimodal route prediction model consists of a

combination of route embeddings (based on node and

edge embeddings) along with relevant contextual in-

formation. The model’s output includes several route-

related metrics as outlined in subsection 2.4. The

multi-task model performs regression predictions for

metrics such as distance, travel duration, CO2 emis-

sions, comfort, safety, mode distribution, and mode

consistency, as well as a classiﬁcation prediction for

the route type label. The model’s optimization param-

eters are detailed in Table 1.

Figure 6 presents the loss function trends for the

various prediction metrics. Initially, the attention

mechanism is employed to help the model focus on

the most relevant parts of the node and edge se-

Table 1: Optimization parameters utilized in the frame-

work’s models.

Learning Rate Batch Size Weight Decay Gradient Clipping

0.001 4 0.0001 5

Table 2: Performance results of the classiﬁcation task after

450 epochs.

Accuracy Recall Precision

0.9 0.75 0.79

quences during route embedding. The CO2 emis-

sions loss curve is the most prominent, ﬂuctuating

signiﬁcantly throughout training, with values ranging

from 0 to 12. These ﬂuctuations indicate varying per-

formance across batches, suggesting that CO2 emis-

sions prediction remains challenging for the model

and may require further tuning to improve stability

in this area. In contrast, other loss components show

much lower values, remaining near zero throughout

the test batches. This minimal variation suggests that

the model has effectively learned these aspects, with

little contribution to the overall error. In Figure 7,

the same losses are plotted without using the atten-

tion mechanism. Here, the CO2 emissions loss curve

shows pronounced instability, with values reaching

as high as 60 and signiﬁcant spikes across the en-

tire batch range. This high variability highlights the

model’s instability without the attention mechanism,

likely due to the model’s reduced ability to consis-

tently focus on the most relevant features. This under-

lines the importance of incorporating attention mech-

anisms into the proposed framework to stabilize and

enhance model performance, particularly for tasks

that demand emphasis on speciﬁc features or relation-

ships within the data.

Table 2 reports the accuracy, recall, and precision

for the classiﬁcation task after 450 epochs. The clas-

siﬁcation accuracy is around 0.9, indicating that the

model is highly effective in making correct predic-

tions. Precision and recall also show high values,

demonstrating strong performance in the classiﬁca-

tion task. For the regression tasks, the R² values are

computed across all metrics. An example of CO2

emissions is shown in Figure 8. The testing R

ﬂuc-

tuates around 0.5 without a clear upward or down-

ward trend, suggesting that the model’s performance

on unseen data remains relatively consistent. Similar

behavior is observed for the other metrics. These ﬂuc-

tuations indicate some instability in the predictions,

implying that while the model generalizes to the test

data, further reﬁnement is necessary to improve sta-

bility and reduce variance during testing.

After training, we also tested our recommenda-

tion system based on Equation 1. The system con-

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

318

Table 3: Recommendation Results. The ranking of four itineraries when the starting point is the stop at node 51 and the

destination is the Strasbourg campus located at node 44.

Ranks

CO2

(gram/km)

Safety

Distance

(km)

Score

Duration

(min)

Mode Distribution Context

1 9.67 0.67 0.79 5.29 1.99 walk Snow, Morning

2 15.45 0.24 0.72 8.04 7.25 Bus, walk Snow, Morning

3 16.4 0.21 0.84 9.5 8.01 Bus Snow, Morning

5 16.7 0.21 0.87 9.87 8.9 Bus Snow, Morning

siders multiple factors when making route recom-

mendations, including CO2 emissions, user safety,

and distance. These parameters are integrated into

the ranking algorithm to ensure that suggested routes

not only optimize efﬁciency but also prioritize en-

vironmentally friendly options and user well-being.

This holistic approach allows users to make informed

choices based on their preferences for sustainability

and safety. The recommendation system results are

presented in Table 3, where weights of 0.5, 0.3, and

0.2 were assigned to CO2 emissions, safety, and dis-

tance, respectively. The results reveal that distance is

not the primary criterion for selecting the top-ranked

route; instead, CO2 emissions and safety factors are

more heavily weighted. This outcome underscores

the emphasis on environmental impact and user safety

in the recommended routes.

4 CONCLUSION

This paper presents a novel approach to multimodal

route recommendation that utilizes advanced graph-

based learning techniques, speciﬁcally GRU and

GCN models, to improve the effectiveness and rele-

vance of route suggestions in urban environments. By

modeling the transport network as a complex graph

and incorporating essential contextual factors such as

weather, safety, and passenger comfort, our method-

ology captures intricate spatial and temporal patterns

often overlooked by traditional systems. The pro-

posed recommendation system is grounded in a multi-

task model that predicts key urban metrics, includ-

ing route distance, travel duration, CO2 emissions,

comfort, safety, mode distribution, mode consistency,

and route type. Experimental results demonstrate

high classiﬁcation accuracy, highlighting the model’s

strong performance in predicting route types. These

predicted factors are integrated into our system to

ensure the suggested routes prioritize environmental

sustainability and user well-being. The ranked routes

show that CO2 emissions and safety take precedence

over distance, aligning with our objective of promot-

ing eco-friendly transportation choices. Our work

contributes to the growing body of knowledge on in-

telligent transportation systems and provides a robust

framework for future research in this domain. Future

perspectives will focus on enhancing the model’s per-

formance by exploring additional graph properties.

REFERENCES

Candra, A., Budiman, M. A., and Hartanto, K. (2020). Di-

jkstra’s and a-star in ﬁnding the shortest path: A tuto-

rial. In 2020 International Conference on Data Sci-

ence, Artiﬁcial Intelligence, and Business Analytics

(DATABIA), pages 28–32. IEEE.

Chen, L., Zhang, L., Cao, S., Wu, Z., and Cao, J. (2020).

Personalized itinerary recommendation: Deep and

collaborative learning with textual information. Ex-

pert Systems with Applications, 144:113070.

da Silva, E. S., Pedrini, H., and dos Santos, A. L. (2023).

Applying graph neural networks to support decision

making on collective intelligent transportation sys-

tems. IEEE Transactions on Network and Service

Management, 20(4):4085–4096.

Ding, R., Ujang, N., Hamid, H. B., Manan, M. S. A., Li,

R., Albadareen, S. S. M., Nochian, A., and Wu, J.

(2019). Application of complex networks theory in

urban trafﬁc network researches. Networks and Spa-

tial Economics, 19:1281–1317.

Geisberger, R., Sanders, P., Schultes, D., and Vetter, C.

(2012). Exact routing in large road networks us-

ing contraction hierarchies. Transportation Science,

46(3):388–404.

Ghalmane, Z., Brahmia, M.-E.-A., Zghal, M., and Cher-

iﬁ, H. (2022). A stochastic approach for extracting

community-based backbones. In International Con-

ference on Complex Networks and Their Applications,

pages 55–67. Springer.

Ghalmane, Z., Cheriﬁ, C., Cheriﬁ, H., and El Hassouni, M.

(2020). Exploring hubs and overlapping nodes inter-

actions in modular complex networks. IEEE Access,

8:79650–79683.

Ghalmane, Z., Cheriﬁ, C., Cheriﬁ, H., and El Hassouni,

M. (2021). Extracting modular-based backbones in

weighted networks. Information Sciences, 576:454–

474.

Ghalmane, Z., Cheriﬁ, C., Cheriﬁ, H., and Hassouni,

M. E. (2019). Centrality in complex networks with

overlapping community structure. Scientiﬁc reports,

9(1):10133.

Graph-Based Learning for Multimodal Route Recommendation

319

Ghalmane, Z., El Hassouni, M., Cheriﬁ, C., and Cher-

iﬁ, H. (2018a). K-truss decomposition for modular

centrality. In 2018 9th International Symposium on

Signal, Image, Video and Communications (ISIVC),

pages 241–248. IEEE.

Ghalmane, Z., El Hassouni, M., and Cheriﬁ, H. (2018b).

Betweenness centrality for networks with non-

overlapping community structure. In 2018 IEEE

workshop on complexity in engineering (COMPENG),

pages 1–5. IEEE.

GHALMANE, Z., Zghal, M., et al. (2023). Road networks:

A new ﬁltering approach to extract backbones using

community structure.

Hamilton, W., Ying, Z., and Leskovec, J. (2017). Inductive

representation learning on large graphs. Advances in

neural information processing systems, 30.

Hopman, D., Koole, G., and Mei, R. V. D. (2021). A

machine learning approach to itinerary-level booking

prediction in competitive airline markets. Interna-

tional Journal of Revenue Management, 12(3-4):153–

191.

Iqbal, M., Zhang, K., Iqbal, S., and Tariq, I. (2018). A fast

and reliable dijkstra algorithm for online shortest path.

Int. J. Comput. Sci. Eng, 5(12):24–27.

Jana, D., Malama, S., Narasimhan, S., and Taciroglu, E.

(2023). Edge ranking of graphs in transportation net-

works using a graph neural network (gnn). arXiv

preprint arXiv:2303.17485.

Jiang, W. and Luo, J. (2022). Graph neural network for

trafﬁc forecasting: A survey. Expert systems with ap-

plications, 207:117921.

Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-

siﬁcation with graph convolutional networks. arXiv

preprint arXiv:1609.02907.

Latora, V., Nicosia, V., and Russo, G. (2017). Complex net-

works: principles, methods and applications. Cam-

bridge University Press.

Liu, H., Tong, Y., Zhang, P., Lu, X., Duan, J., and Xiong,

H. (2019). Hydra: A personalized and context-aware

multi-modal transportation recommendation system.

In Proceedings of the 25th ACM SIGKDD Interna-

tional Conference on Knowledge Discovery & Data

Mining, pages 2314–2324.

Liu, S. and Jiang, H. (2022). Personalized route recommen-

dation for ride-hailing with deep inverse reinforce-

ment learning and real-time trafﬁc conditions. Trans-

portation Research Part E: Logistics and Transporta-

tion Review, 164:102780.

MOEZZI, R. Enhanced vehicle arrival time prediction with

graph neural networks (gnn) using gps data.

Shaﬁque, S. and Ali, M. E. (2016). Recommending most

popular travel path within a region of interest from

historical trajectory data. In Proceedings of the 5th

ACM SIGSPATIAL International Workshop on Mobile

Geographic Information Systems, pages 2–11.

Shanmukhappa, T., Ho, I. W.-H., Chi, K. T., and Leung,

K. K. (2019). Recent development in public transport

network analysis from the complex network perspec-

tive. IEEE Circuits and Systems Magazine, 19(4):39–

65.

Sharma, A., Sharma, A., Nikashina, P., Gavrilenko, V., Tse-

lykh, A., Bozhenyuk, A., Masud, M., and Meshref, H.

(2023). A graph neural network (gnn)-based approach

for real-time estimation of trafﬁc speed in sustainable

smart cities. Sustainability, 15(15):11893.

Song, C., Guan, W., and Ma, J. (2018). Potential travel

cost saving in urban public-transport networks using

smartphone guidance. Plos one, 13(5):e0197181.

Termos, M., Ghalmane, Z., Fadlallah, A., Jaber, A.,

Zghal, M., et al. (2023). Intrusion detection system

for iot based on complex networks and machine

learning. In 2023 IEEE Intl Conf on Depend-

able, Autonomic and Secure Computing, Intl Conf

on Pervasive Intelligence and Computing, Intl

Conf on Cloud and Big Data Computing, Intl

Conf on Cyber Science and Technology Congress

(DASC/PiCom/CBDCom/CyberSciTech), pages

0471–0477. IEEE.

Termos, M., Ghalmane, Z., Fadlallah, A., Jaber, A., Zghal,

M., et al. (2024). Gdlc: A new graph deep learn-

ing framework based on centrality measures for in-

trusion detection in iot networks. Internet of Things,

26:101214.

Wang, Y., Yin, H., Chen, H., Wo, T., Xu, J., and Zheng, K.

(2019). Origin-destination matrix prediction via graph

convolution: a new perspective of passenger demand

modeling. In Proceedings of the 25th ACM SIGKDD

international conference on knowledge discovery &

data mining, pages 1227–1235.

Wei, L.-Y., Zheng, Y., and Peng, W.-C. (2012). Con-

structing popular routes from uncertain trajectories. In

Proceedings of the 18th ACM SIGKDD international

conference on Knowledge discovery and data mining,

pages 195–203.

Yu, Y., Si, X., Hu, C., and Zhang, J. (2019). A review of

recurrent neural networks: Lstm cells and network ar-

chitectures. Neural computation, 31(7):1235–1270.

Yuan, J., Zheng, Y., Zhang, C., Xie, W., Xie, X., Sun, G.,

and Huang, Y. (2010). T-drive: driving directions

based on taxi trajectories. In Proceedings of the 18th

SIGSPATIAL International conference on advances in

geographic information systems, pages 99–108.

Zanin, M. and Lillo, F. (2013). Modelling the air transport

with complex networks: A short review. The Euro-

pean Physical Journal Special Topics, 215(1):5–21.

Zhang, S., Tong, H., Xu, J., and Maciejewski, R. (2019).

Graph convolutional networks: a comprehensive re-

view. Computational Social Networks, 6(1):1–23.

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

320