Interference-Based Reliability and Capacity Analysis for IEEE 802.11

Broadcast Ad-Hoc Networks on the Highway

Zhijuan Li

1,2 a

, Xintong Wu

, Xiaokun Li

1,2,3 b

and Xiaomin Ma

Department of Computer and Big Data, Heilongjiang University, Harbin 150080, China

Postdoctoral Program of Heilongjiang Hengxun Technology Co., Ltd. Harbin 150090, China

School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China

College of Science and Engineering, Oral Roberts University, Tulsa, OK 74171, U.S.A.

lizhijuan@hrbeu.edu.cn, {wuxintong, lixiaokun}@hlju.edu.cn, xma@oru.edu

Keywords:

Vehicular Ad-Hoc Network, CSMA, SINR, Reliability, Capacity.

Abstract:

Interference is a critical factor that degrades wireless network performance. In IEEE 802.11 wireless broad-

cast networks, hidden terminals and concurrent transmissions are the primary sources of interference due to

the carrier sense multiple access (CSMA) mechanism. Therefore, analyzing the signal-to-interference-plus-

noise ratio (SINR) distribution is essential for evaluating network performance, whose derivation relates to

the transmission probabilities of hidden terminals and concurrent transmissions. In this study, we utilize the

existing semi-markov process (SMP) model to calculate these transmission probabilities. Subsequently, we

employ the Laplace transform to analyze the SINR distribution in IEEE 802.11 broadcast ad-hoc networks

on highways. Based on the derived SINR distribution, we further evaluate the reliability and capacity. This

approach can be readily extended to two-dimensional (2D) or three-dimensional (3D) scenarios by employ-

ing d-dimensional (1 ≤ d ≤ 3, dD) point process. Experimental results demonstrate that the proposed model

achieves high accuracy under small to medium interference ranges. Additionally, the analysis remains highly

accurate for receivers within 70 meters, even in scenarios with large interference ranges.

1 INTRODUCTION

Vehicular ad-hoc Networks (VANETs), based on

IEEE 802.11p/bd, deliver broadcast services for

safety-related applications with strict quality of ser-

vice (QoS) requirements. IEEE 802.11p/bd deﬁnes

physical and Medium Access Control (MAC) layer

speciﬁcations, with 802.11bd enhancing physical

layer performance as 802.11p’s successor. The MAC

layer employs the distributed coordination function

(DCF), which relies on CSMA for collision avoid-

ance. However, vehicle-to-vehicle (V2V) commu-

nication using CSMA suffers from hidden terminal

and concurrent collision problems, degrading chan-

nel quality and causing packet loss (Yin et al., 2013).

Performance evaluation is thus vital for network plan-

ning and optimization (Luong et al., 2017; Li et al.,

2020). Common reliability metrics include Node-to-

Node Packet Reception Probability (PRP) and Packet

Reception Ratio (PRR), which measure the probabil-

https://orcid.org/0000-0002-2162-5654

https://orcid.org/0000-0002-6645-6890

ity that a packet is received successfully from differ-

ent aspects (Ma et al., 2012).

Researchers have built many analytical models

to derive reliability metrics of V2V communication.

Some models adopted a deterministic distance-based

method, and other models adopted the SINR-based

method. In models using deterministic distance-based

methods, a packet is considered lost if a collision hap-

pens during the transmission of the packet (Li et al.,

2022). The size of the geometric region that may

cause packet collision, such as length, area, volume,

etc. needs to be calculated (Zhao et al., 2020). In

SINR-based models, a packet transmission is consid-

ered successfully received as long as the SINR ex-

ceeds the threshold throughout the packet’s transmis-

sion, even if a collision occurs, reﬂecting real-world

conditions more accurately. Thus, SINR-based model

is developed as a more general and accurate model

for analyzing the performance of wireless broadcast

network compared to the deterministic distance-based

model (Li et al., 2022). The critical step in the SINR-

based method is deriving the distribution of SINR,

namely probability density function (PDF) and cumu-

520

Li, Z., Wu, X., Li, X. and Ma, X.

Interference-Based Reliability and Capacity Analysis for IEEE 802.11 Broadcast Ad-Hoc Networks on the Highway.

DOI: 10.5220/0013356400003941

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 11th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2025), pages 520-528

ISBN: 978-989-758-745-0; ISSN: 2184-495X

lative distribution function (CDF) of the SINR at the

receiver (Zhao et al., 2021a; Ma and Trivedi, 2021).

Stochastic geometry is a powerful tool for an-

alyzing the distribution of SINR. The application

of stochastic geometric analysis hinges on calcu-

lating the transmission probability of a node under

the CSMA mechanism. Most stochastic geometry-

based analytical models for evaluating wireless net-

work performance under CSMA use ALOHA as an

approximation. This approach has been applied to

one-dimensional (1D) VANETs (Błaszczyszyn et al.,

2013), intersection VANET (Ni et al., 2015a; Stein-

metz et al., 2015; Belmekki et al., 2020; Kimura and

Saito, 2022), and general urban road VANET (Kimura

et al., 2016). Recently, Kimura et al. (Kimura

and Saito, 2022) proposed a broadcast rate optimiza-

tion scheme for intersections using this approach, di-

viding roads into queuing and running segments to

provide closed-form approximations for key perfor-

mance metrics.

Meanwhile, other stochastic geometry-based

models directly analyze CSMA behavior to evaluate

SINR distribution and network performance. For ex-

ample, Nguyen et al. (Nguyen et al., 2007) mod-

eled CSMA using a Mat

ern-II-continuous process, as-

signing nodes uniformly distributed backoff counters

in [0,1]. Tong et al. (Tong et al., 2016) improved

this by developing a Mat

ern-II-discrete process to

better capture discrete backoff counters and analyze

packet transmission success probability in a highway

VANETs. They utilized simulation methods to esti-

mate node transmission probabilities. Unlike previ-

ous studies that approximated CSMA with ALOHA,

their work directly models the CSMA mechanism,

providing valuable insights that have inspired our re-

search.

Considering that the SMP model (Yin et al., 2013)

characterized the CSMA behavior, the steady-state

transmission probability of a node can be calculated.

Then the transmission probabilities of hidden termi-

nals and concurrent transmissions during the trans-

mission of the tagged sender can be obtained by

the SMP model. On the basis of the SMP model,

the probability derivation-based method, the effec-

tive interference distance-based method are two other

mathematical methods to analyze the SINR distribu-

tion of V2V communication in IEEE 802.11 VANET.

Zhao et al. (Zhao et al., 2021a) built the probability

derivation-based method to analyze the performance

of VANET at 1D highway by adopting order statistics

and non-homogeneous poisson point process (NHPP)

distribution and extended the approach to analyze the

case of 2D intersections. However, the probability

derivation method has high computational complex-

ity and requires parallel computing to solve the SINR

distribution, which increases the difﬁculty of imple-

mentation and requires a server with parallel comput-

ing power (Zhao et al., 2021a; Zhao et al., 2021b).

In recent years, Ma et al. (Ma et al., 2021; Ma

and Trivedi, 2021) introduced an efﬁcient interference

distance-based method to evaluate reliability metrics

such as PRP and PRR by calculating the effective in-

terference range related to the SINR threshold. Build-

ing on this, Li et al. (Li et al., 2022) reﬁned the model

by incorporating a maximum interference range con-

straint and extended it to analyze the case of 2D in-

tersection VANETs, proposing the SINR-related Ef-

fective Distance Constrained by Maximum interfer-

ence range (SED-CM) model. This model assumes

that reception fails if interference occurs within the

effective interference range, consistent with determin-

istic distance-based principles. This approach allows

for rapid computation of PRP and PRR by bypassing

complex integrals. However, determining link capac-

ity requires numerous time-consuming interpolations,

and extending the model to higher dimensions is chal-

lenging due to the complexity of computing geomet-

ric region sizes (Zhao et al., 2020).

In this paper, we propose applying stochastic ge-

ometry methods and the SMP model to compute

the SINR distribution. Speciﬁcally, we employ the

Laplace transform to analyze the SINR distribution,

accounting for the effects of hidden terminals and

concurrent transmissions. Based on the derived SINR

distribution, we further calculate reliability metrics

and network capacity. The contributions of the paper

are as follows.

1) Firstly, we adopt the stochastic geometry method

to derive the SINR distribution at the receiver

in V2V communication with CSMA mechanism.

We evaluate the interference probability of other

nodes by the SMP model which captures the full

CSMA behavior.

2) Secondly, based on the obtained SINR distribu-

tion, we further derive the reliability metrics PRP,

PRR, and link capacity.

3) Thirdly, we conduct a series of experiments to val-

idate the model with NS2 simulation.

The rest of the paper is organized as follows. Sec-

tion 2 describes the system model, including the com-

munication scenario and interference model. Section

3 gives the analysis of SINR distribution conditioned

on the receiving distance. Section 4 presents the re-

liability metrics PRP, PRR as well as link capacity.

Section 5 describes the experimental process and re-

sults. Section 6 concludes the paper.

Interference-Based Reliability and Capacity Analysis for IEEE 802.11 Broadcast Ad-Hoc Networks on the Highway

521

Area RCArea LCArea LH Area RH

,…,k

,… 1

,…,l

,…

𝐼

Figure 1: General interfering scenario of IEEE 802.11

broadcast ad-hoc networks on the highway.

2 SYSTEM MODEL

In the paper, we consider V2V communication in a

highway scenario. As shown in Fig. 1, the high-

way scenario is abstracted to a 1D line. The num-

ber of nodes follows the 1D homogeneous poisson

point process (HPPP) with the density β (vehs/m).

Vehicles periodically broadcast/receive Basic Safety

Messages (BSMs) to/from nearby vehicles. T is the

tagged sender, R is the tagged receiver. d

is the dis-

tance from the sender T to the receiver R. r

presents

the carrier sensing range. r

is the interference range.

We assume signal propagation suffers from Rayleigh

fading. In this way, the receiving power P

at a dis-

tance d from the sender is:

(d) = P

ηd

−α

h (1)

where P

is the transmission power, η = Kd

, K is a

constant determined by the device, α is the path loss

exponent, d

is the reference distance, and h is a ran-

dom variable following the exponential distribution

with a mean of one. The sensing range can be com-

puted by r

= d

K/P

, P

is the carrier sensing

threshold.

During the transmission of T ’s packet, R can also

receive signals sent from other nodes except T , reduc-

ing the SINR of T ’s transmission. The expression of

SINR is:

SINR =

∑

+ N

ηd

−α

∑

+ N

(2)

where N

is the power of noise, I

∑

is the total interfer-

ence power.

Under the effect of CSMA, the interferers are clas-

siﬁed into two classes: concurrent transmissions and

hidden terminal (Yin et al., 2013). The hidden ter-

minal area is beyond the sensing range of the tagged

sender and within the interference range. The con-

current transmission area is within the sensing range

of the tagged sender. Then, we split four interference

areas for the receiver R: Left Hidden (LH) terminal

area, Left Concurrent (LC) transmission area, Right

Concurrent (RC) transmission area, and Right Hid-

den (RH) terminal area, as shown in Fig. 1. The

tagged sender T is the origin. Area LH is within the

range of [−r

+ d

,−r

], area LC is within the range

of [−r

], area RC is within the range of [d

and area RH is within the range of [r

+ d

) represents the interference node in area

LH(RH). Assuming that there are l(l

′

) nodes in area

LH(RH), d

= 1, ··· ,l)(d

= 1, ··· ,l

′

)) denote

the distance between the receiver R and the I

)-th

node within area LH(RH). We have d

≤ d

≤ r

− d

≤ d

≤ r

In the same way, I

) represents the interference

node in area LC(RC). Assuming that there are k nodes

in area LC, d

= 1,··· ,k)(d

= 1,··· ,k

′

))

denote the distance between the receiver R and the

)-th node with area LC(RC). We have 0 ≤ d

≤

+ r

and 0 ≤ d

≤ r

− d

Furthermore, the proportion of nodes in differ-

ent interference regions contributing to aggregate in-

terference is denoted as: g

(X ∈ [LH, LC,RC,RH]).

The expression of g

is as follows.



X ∈ [LC,RC]

X ∈ [LH,RH]

(3)

where p

presents the hidden terminal transmission

probability during the vulnerable period. and π

rep-

resents the probability that a neighbor starts to trans-

mit a packet at the beginning of the same time slot

with the tagged vehicle. We calculate p

and π

by solving the steady-state probability π

XMT

that the

node is in the transmitting state in the SMP model

(Yin et al., 2013).

3 SINR CONDITIONAL

DISTRIBUTION ANALYSIS

In the section, we derive the CDF and PDF of SINR

at the receiver by utilizing the Laplace transform of

overall interference at the receiver.

3.1 The CDF and PDF of SINR at the

Receiver

As shown in Fig. 1, T is the tagged sender, R is the

receiver. d

is the distance between T and R. Accord-

ing to the deﬁnition of SINR in (2), the CDF of SINR

conditioned on receiving distance d

is:

SINR

(x|d

) = P(SINR ≤ x|d

)

= 1 − P(SINR > x|d

)

= 1 − P



ηhd

−α

+ I

+ L

+ N

> x



(4)

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

522

and the PDF of SINR conditioned on receiving dis-

tance d

is:

SINR

(x|d

) =

SINR

(x|d

)

(5)

In (4), N

is the noise power. I

)

represent the accumulated interference from area LH

(LC,RC,RH) on the receiver, which are given by

∑

∈Φ

ηd

; I

∑

∈Φ

ηd

(6)

∑

∈Φ

ηd

; I

∑

∈Φ

ηd

(7)

In this way, we can rewrite (4) as

SINR

(x|d

) =

1 − E





h >

+ I

+ N

)





(8)

Due to Rayleigh fading, h ∼ exp(1), let ∆ = xd

we get

SINR

(x|d

) = 1 − exp



−

∆



× E



exp



−

∆

ηI



exp



−

∆



exp



−

∆



exp



−

∆





(9)

and using the independence of hidden terminal and

concurrent transmission, we ﬁnally have that

SINR

(x|d

) = 1 − exp



−

∆





∆





∆





∆





∆



(10)

where L

(

∆

) is the Laplace transform of I

, which

can be interpreted as follows: the Laplace transform

of I

is the reduction in the probability that SINR is

greater than a given threshold due to interference from

area LH; the Laplace transform of I

is the reduction

in the probability that SINR is greater than a given

threshold due to interference area LC; the Laplace

transform of I

is the reduction in the probability

that SINR is greater than a given threshold due to in-

terference area RC; the Laplace transform of I

the reduction in the probability that SINR is greater

than a given threshold due to interference area RH;

and exp



−

∆



can be regarded as a case without

interference.

We are now ready to determine expressions for

(

∆

), L

(

∆

), L

(

∆

), and L

(

∆

). We

derive L

(

∆

), L

(

∆

) by considering the effect

of interference from concurrent transmissions. Sim-

ilarly, we derive L

(

∆

), L

(

∆

) by considering

the effect of interference from hidden terminals.

3.2 Effect of Interference from

Concurrent Transmissions

1) First, considering the probability of concurrent

transmissions, the Laplace transform of the aggregate

interference originating from area LC is given by

(

∆

) = E



exp(−

∆

)



= E

∏

∈Φ

exp



−

∆

ηd

−α



(a)

= E

∏

∈Φ

(exp(−∆d

−α

))

(b)

= exp



−

1 − exp(−∆d

−α

βdd



(c)

= exp





−βg



1 − exp(−∆d

−α







= exp





−βπ



1 − exp(−∆d

−α







(11)

where (a) holds due to the independence of the fading

parameters, (b) uses the expression of the probabil-

ity generating functional (PGFL) for a PPP. (c) holds

conditional on h.

The integral on the right-hand side of (11) is cal-

culated as



1 − exp(−∆d

−α



(e)

)



1 − exp



−∆hy

−1



δy

δ−1

( f )

∞

)

−α

(1 − exp(−∆hx))δx

−δ−1

(g)

= (exp(−∆hx) − 1)x

−δ



∞

)

−α

∞

)

−α

−δ

∆hexp(−∆hx)dx

= (1 − exp(−∆h(d

+ r

)

−α

))(d

+ r

(∆h)

Γ(1 − δ,(d

+ r

)

−α

)

(12)

Interference-Based Reliability and Capacity Analysis for IEEE 802.11 Broadcast Ad-Hoc Networks on the Highway

523

where (e) from the substitution y ← d

, δ

def

= 1/α, (f)

from x ← y

−1

, and (g) from the integration by parts.

Γ(a,b) =

∞

a−1

−u

du represents the upper incom-

plete Gamma function. With the expectation over h,

we obtain

(

∆

) = exp



−βπ



(1 − exp(−∆E(h)(d

+ r

)

−α

))

+ r

) + ∆

E(h

)Γ(1 − δ, (d

+ r

)

−α

i

(13)

where h is exponential, E(h

) =

∞

−z

dz = Γ(1 +

δ), and E(h) =

∞

−z

dz = Γ(2). After a series of

derivations,

(

∆

) = exp



−βπ



(1 − A

′

)(d

+ r

∆

Γ(1 + δ)Γ



1 − δ,(d

+ r

)

−α



i

(14)

where A

′

= exp(−∆Γ(2)(d

+ r

)

−α

Substituting ∆ = xd

yields the desired result:

(

) = exp (−βπ

[(1 − A)(d

+ r

(xd

η)

Γ(1 + δ)Γ



1 − δ,(d

+ r

)

−α



i

(15)

where A = exp(−xΓ(2)(

)

−α

2) Similar to the derivation of L

(

∆

), I

(11) is replaced by I

, I

is replaced by I

, the upper

limit of the integral is replaced by r

− d

. After a

series of derivations, we can obtain the Laplace trans-

form of the aggregate interference from area RC as

follows.

(

) = exp (−βπ

[(1 − B)(r

− d

(xd

η)

Γ(1 + δ)Γ



1 − δ,(r

− d

)

−α



i

(16)

where B = exp(−xΓ(2)(

−d

)

−α

3.3 Effect of Interference from Hidden

Terminal

1) Similar to the derivation of L

(

∆

), I

in (11) is

replaced by I

, I

is replaced by I

, π

is replaced by

. The upper limit and lower limit of the integral are

replaced by r

and r

, respectively. After a series

of derivations, we can obtain the Laplace transform of

the aggregate interference from area LH as follows.

(

) = exp (−βp

[(A − 1)(d

+ r

)−

(C − 1)r

+ (xd

η)

Γ(1 + δ)[γ(1 − δ, (d

+ r

)

−α

)−

γ(1 − δ,r

−α

)]



(17)

where C = exp(−xΓ(2)(

)

−α

2) Similar to the derivation of L

(

∆

), I

(11) is replaced by I

, I

is replaced by I

, π

replaced by p

. The upper limit and lower limit of

the integral are replaced by r

and r

− d

, respec-

tively. After a series of derivations, we can obtain the

Laplace transform of the aggregate interference from

area RH as follows.

(

) = exp



−βp

(B − 1)(d

+ r

)

−

(C − 1)r

+ (xd

η)

Γ(1 + δ)[γ(1 − δ, (d

+ r

)

−α

)−

γ(1 − δ,r

−α

)]



(18)

where B is the same as in (16) and C is the same as in

(17).

4 RELIABILITY AND CAPACITY

ANALYSIS

Based on the above analysis of SINR distribution con-

ditioned on the receiving distance, we give the expres-

sions of reliability metrics PRP, PRR, and link capac-

ity.

4.1 PRP

PRP refers to the probability that a node within the

transmission range of the sender successfully receives

a packet. It equals the probability that the SINR of a

tagged receiver exceeds a threshold θ, i.e.,

PRP(d

) = P(SINR > θ|d

) = 1 − F

SINR

(θ|d

)

(19)

Then we obtain PRP by substituting θ for x in (10).

4.2 PRR

PRR is deﬁned as the percentage of nodes that suc-

cessfully receive a packet from the tagged transmitter

among the neighbors. PRR could be expressed as a

function of PRP, as follows:

PRR(d

) =

βPRP(x)dx

βd

PRP(x)dx

(20)

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

524

4.3 Link Capacity

4.3.1 Unconditional SINR Distribution

The CDF and PDF of SINR unconditioned is:

SINR

(x) =

SINR|d

(x) f

(t)dt

SINR

(x) =

SINR

(t)dt

(21)

where f

(x) is the receiving distance distribution.

Next we derive f

(x) using an order statistic method

similar to the derivation process in (Zhao et al.,

2021a). The difference is that (Zhao et al., 2021a)

assumes that the vehicle position follows the NHPP

distribution, while this paper assumes that it follows

the HPP distribution.

4.3.2 Receiving Distance Distribution

is the distance between T and R. Independent ran-

dom variables 0 ≤ S

,·,S

≤ r

denote unordered

distances between T and the nodes in the right sens-

ing region. The cumulative probability distribution

P(S

≤ r) is given by Theorem 6.2 in (Trivedi, 2008):

(r) = P(S

≤ r|N(s) = 1)

P[N(r) = 1, N(s) − N(r) = 0]

P[N(s) = 1]

,i = 1, ...,l.

(22)

Then the PDF of S

is:

(r) =

.0 ≤ r ≤ r

,i = 1, ··· ,l

(23)

Then according to Theorem 6.2 in (Trivedi, 2008),

(i = 1,...,l) are the order statistics of the random

variables S

(i = 1,...,l). Thus, the CDF and PDF of

distance d

(0 ≤ d

≤ r

) can be calculated as

(τ) = P(d

≤ τ) =

∑

j=i





(τ)[1 − F

(τ)]

l− j

(τ) =

(τ)

dτ

, 0 ≤ τ ≤ r

(24)

The probability that there are l nodes in the right

sensing area is P[l,(0,r

)] =

(βr

)

−βr

. Then, the to-

tal d

’s PDF can be expressed as

(x) =

∞

∑

l=1

P[l,(0,r

)]

∑

i=1

(x)p

, (25)

where p

is the probability that the receiver R is the

i-th node within the right sensing area, which is eval-

uated as p

= 1/l(i = 1,...,l). So, the d

’s PDF can

be solved as follows.

(x) =

∞

∑

l=1

P[l,(0,r

)]

∑

i=1

(x)

= f

(x) =

, 0 ≤ x ≤ r

(26)

4.3.3 Link Capacity

The distribution and expectation of the link capacity

are given in (Ni et al., 2015b). The CDF of the link

capacity is as follows.

(x) = P{W log

(1+SINR) < x} = F

SINR



− 1



(27)

where W is the bandwidth, c is the link capacity. The

PDF of the link capacity is

(x) =

ln2

· 2

−1

SINR

−1

) (28)

5 EXPERIMENT

5.1 Experiment Settings

We use Matlab programs to compute the proposed an-

alytical model in which inputs are the communication

parameters and outputs are the CDF and PDF of SINR

as well as the reliability metrics: PRP, PRR, and link

capacity. Then we conduct a series of experiments to

compare the proposed model with NS2 simulation. In

the simulation, we deploy the nodes following HPPP

on a circular lane with a length of 10 km with a den-

sity of 0.1 vehs/m. The 10 km simulation scenario

is large enough to objectively evaluate the impact of

the interference. The other communication parame-

ters are set as follows: the data rate R

is 24 Mbps,

the carrier frequency f is 5.9 GHz, the channel band-

width is 10 MHz, the transmission power P

is 26

dBm, the carrier sensing threshold P

is -75 dBm, the

mean receiving distance R

where the average receiv-

ing power equals the sensing threshold is 500 m, the

power of noise N

is -99 dBm, the reference distance

is 1 m, the transmit gain and the receiver gain are

both 1.0, constant η is 1.64 × 10

−5

, the size of the

competition window W is 16, the path loss exponent

α is 2, the DIFS is 58 µs, the packet length is 200

Bytes, the slot time σ is 13 µs, the packet generation

rate λ is 10 Hz.

Interference-Based Reliability and Capacity Analysis for IEEE 802.11 Broadcast Ad-Hoc Networks on the Highway

525

-10 0 30 40

SINR(dB)

0.01

0.02

0.03

0.04

PDF

(a)

-10 0 10 20 30 40

SINR(dB)

0.2

0.4

0.6

0.8

CDF

(b)

Figure 2: PDF and CDF of SINR conditioned on the receiving distance d

while r

equals 500 m. (a) PDF. (b) CDF.

-10 0 10 20 30 40

SINR(dB)

0.005

0.01

0.015

0.02

0.025

0.03

PDF

(a)

-10 0 10 20 30 40

SINR(dB)

0.2

0.4

0.6

0.8

CDF

(b)

Figure 3: PDF and CDF of SINR conditioned on the receiving distance of 150 m with different interference range r

. (a) PDF.

(b) CDF.

5.2 Experiment Results

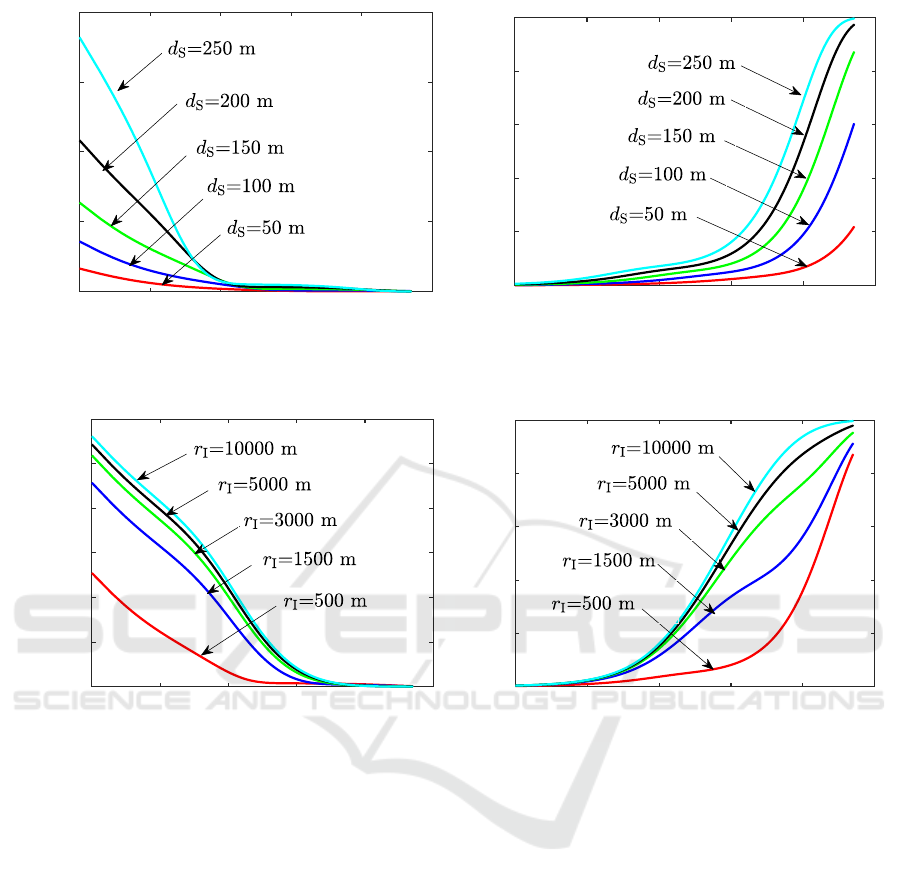
5.2.1 PDF and CDF of SINR

Fig. 2a and Fig. 2b present the PDF and CDF of

SINR within 37 dB when the receiving distance d

equals 50 m, 100 m, 150 m, 200 m, and 250 m, re-

spectively. The minimum interference power is equal

to the carrier sensing threshold. In this way, the inter-

ference range r

is equal to the sensing range, which

is equal to 500 m. We observe that a smaller receiving

distance d

corresponds to a larger mean of SINR, and

otherwise, a larger receiving distance d

corresponds

to a smaller average value of SINR. The reason be-

hind this phenomenon is that the smaller the receiv-

ing distance d

, the less power attenuation between

the sender and the receiver, resulting in larger receiv-

ing power and SINR.

Fig. 3a and Fig. 3b present the PDF and CDF

of SINR within 37 dB when the receiving distance d

equals 150 m, and the interference ranges r

are set

to be 500 m, 1500 m, 3000 m, 5000 m, and 10000

m, respectively. We witness that the greater the in-

terference range, the smaller the mean of SINR. This

is expected because more interference would reduce

the value of SINR when increasing the interference

range. At the same time, we carefully observe the gap

between different curves corresponding to r

and ﬁnd

that the gap is getting smaller and smaller with the

increase in the interference range. The phenomenon

occurs connecting that the interference power is get-

ting smaller and smaller with the increase in the in-

terference distance due to the effect of the attenuation

and path loss of signal propagation. In this way, the

distribution of SINR would tend to be stable when the

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

526

0 50 100 150 200 250 300

0.2

0.4

0.6

0.8

PRP

= 500 m

= 1000 m

= 1500 m

= 5000 m

SED-CM model

(a)

0 50 100 150 200 250 300

0.4

0.5

0.6

0.7

0.8

0.9

PRR

= 5000 m

= 1500 m

= 500 m

= 1000 m

SED-CM model

(b)

Figure 4: PRP and PRR comparisons between the proposed model, NS2 and the model in (Li et al., 2022), SINR threshold θ

= 25 dB. (a) PRPs. (b) PRRs.

interference range reaches a certain level.

5.2.2 PRP and PRR Comparisons

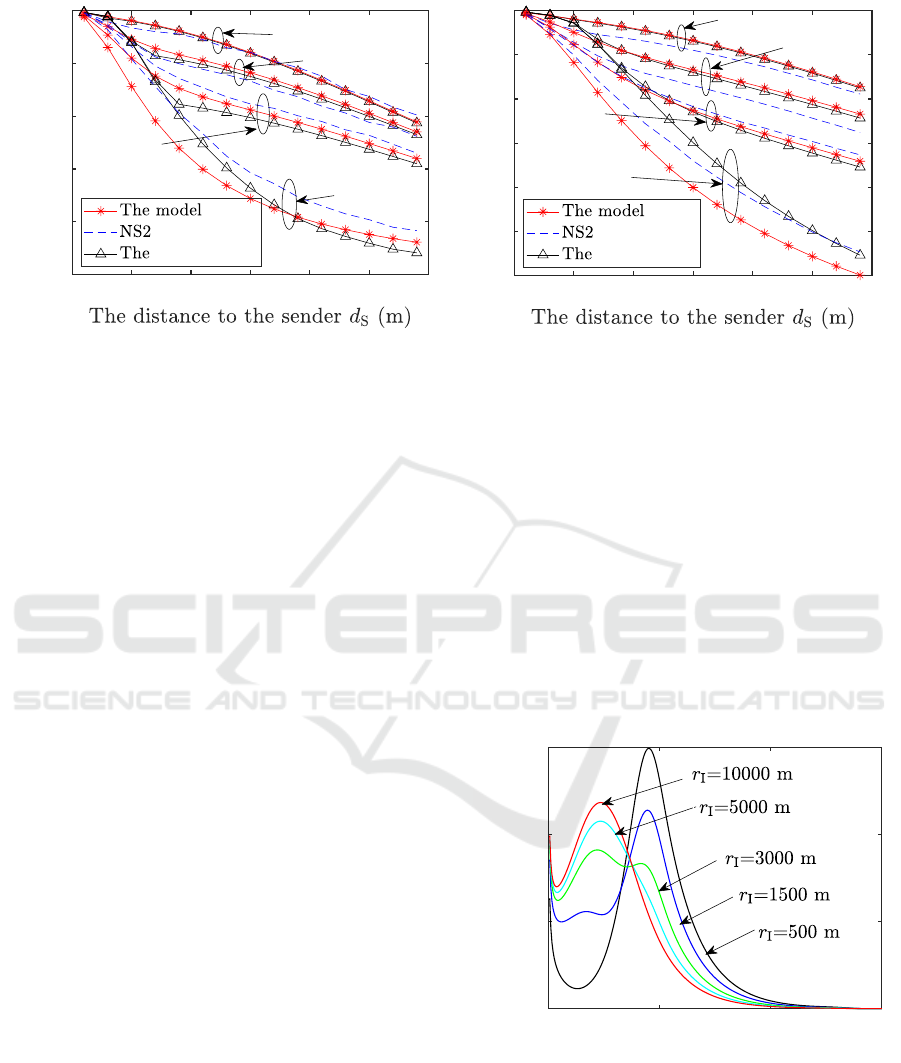
We compute and compare the PRPs and PRRs of the

proposed model, NS2 simulation, and the SED-CM

model in (Li et al., 2022). PRPs and PRRs at 15 re-

ceiving distances are computed with d

equaling from

10 m to 290 m at an interval of 20 m. The compar-

ison results are shown in Fig. 4 when the density is

0.1 vehs/m, and the SINR threshold θ is equal to 25

dB (corresponding to 316 without dB unit). It can be

seen that PRPs and PRRs present decreasing trends

with the receiving distance increasing. Because the

greater the receiving distance, the smaller the value

of SINR, the more packets are lost. Furthermore, we

present the results under four interference ranges 500

m, 1000 m, 1500 m, and 5000 m. The results show

that the greater the interference range r

, the worse

the reliability.

Moreover, we ﬁnd that PRPs and PRRs of the pro-

posed model are almost in line with the simulation

results and the SED-CM results when the interfer-

ence ranges are 500 m. When the interference ranges

are 1000 m and 1500 m, the results show a slight

difference in PRPs and PRRs between the proposed

model, the NS2 simulation, and the SED-CM model.

At the same time, it seems that the results obtained

by the proposed model are smoother than the SED-

CM model, and have little difference from those of

the SED-CM model.

When the interference range is set to 5000 m, the

simulation results appear more optimistic than those

evaluated by our model, with a larger gap observed

between the two. This discrepancy may arise from an

overestimation of the hidden terminal’s transmission

probability at greater distances, leading to an under-

estimation of successful transmissions. However, we

witness that the PRR of the proposed model is almost

the same as the NS2 simulation within 70 m, which is

the range of interest of emergency since closer inter-

ference dominates for close receivers.

Additionally, the SED-CM model applied to dD

IEEE 802.11 broadcast wireless networks requires

calculating the area or volume of irregular regions

(Zhao et al., 2020). In contrast, the model proposed

in this paper could be adapted to analyze dD scenes

by utilizing the dD point process. We plan to present

this work in the future.

0 100 200 300

Link capacity (Mbps)

0.005

0.01

0.015

PDF

Figure 5: PDF of link capacity.

5.2.3 Link Capacity

Fig. 5 presents the PDF of link capacity in different

interference ranges, 500 m, 1500 m, 3000 m, 5000 m,

and 10000 m, respectively. These curves present sim-

ilar changing trends. It could be seen that the mean of

Interference-Based Reliability and Capacity Analysis for IEEE 802.11 Broadcast Ad-Hoc Networks on the Highway

527

link capacity decreases with the increase in the inter-

ference range.

6 CONCLUSION

The proposed model in the paper uses the stochas-

tic geometry method to evaluate the distribution of

SINR, and then derives reliability metrics PRP, PRR,

and link capacity of 1D IEEE 802.11 broadcast ad-

hoc networks. The experiment results show that the

evaluation is accurate for small and medium-distance

interference ranges. At the same time, the evalu-

ation is also quite accurate in the closer receivers,

even if a larger interference range is assumed. This

model can be extended to evaluate the performance of

d (1 ≤ d ≤ 3)-dimensional (dD) IEEE 802.11 broad-

cast ad-hoc networks by utilizing a dD point pro-

cess. It is also adaptable to emerging 802.11 tech-

nologies, such as orthogonal frequency-division mul-

tiple access (OFDMA), multiple input multiple output

(MIMO), high-order quadrature amplitude modula-

tion (QAM) (1024 ∼ 4096), as well as high-frequency

and high-bandwidth applications. Future work will

focus on exploring these extensions in greater detail.

ACKNOWLEDGEMENTS

This work is supported by the Basic Scientiﬁc

Research Funds of Universities of Heilongjiang

Province (No. 2023-KYYWF-1485).

REFERENCES

Belmekki, B. E. Y., Hamza, A., and Escrig, B. (2020). On

the outage probability of vehicular communications

at intersections over nakagami-m fading channels. In

IEEE 91st VTC Spring, pages 1–5, Antwerp, Belgium.

Błaszczyszyn, B., M

uhlethaler, P., and Toor, Y. (2013).

Stochastic analysis of aloha in vehicular ad hoc net-

works. Annals of telecommunications-Annales des

ecommunications, 68(1-2):95–106.

Kimura, T. and Saito, H. (2022). Theoretical broadcast

rate optimization for v2v communications at inter-

section. IEEE Transactions on Mobile Computing,

21(9):3360–3372.

Kimura, T., Saito, H., Honda, H., and Kawahara, R. (2016).

Modeling urban its communication via stochastic ge-

ometry approach. In 2016 IEEE 84th Vehicular Tech-

nology Conference (VTC-Fall), pages 1–5.

Li, W., Song, W., Lu, Q., and Yue, C. (2020). Reliable

congestion control mechanism for safety applications

in urban vanets. Ad Hoc Networks, 98:102033.

Li, Z., Wang, Y., and Zhao, J. (2022). Reliability Evalua-

tion of IEEE 802.11p Broadcast Ad Hoc Networks on

the Highway. IEEE Transactions on Vehicular Tech-

nology, 71(7):7428–7444.

Luong, H. P., Panda, M., Vu, H. L., and Vo, B. Q. (2017).

Beacon rate optimization for vehicular safety appli-

cations in highway scenarios. IEEE Transactions on

Vehicular Technology, 67(1):524–536.

Ma, X. and Trivedi, K. S. (2021). SINR-Based analysis of

IEEE 802.11p/bd broadcast vanets for safety services.

IEEE Transactions On Network And Service Manage-

ment, 18(3):2672–2686.

Ma, X., Yin, X., and Trivedi, K. S. (2012). On the reliability

of safety applications in vanets. International Journal

of Performability Engineering, 8(2).

Ma, X., Zhao, J., Wang, Y., Zhang, T., and Li, Z. (2021). A

new approach to sinr-based reliability analysis of ieee

802.11 broadcast ad hoc networks. IEEE Communi-

cations Letters, 25(2):651–655.

Nguyen, H. Q., Baccelli, F., and Kofman, D. (2007). A

stochastic geometry analysis of dense IEEE 802.11

networks. In Proc. 26th IEEE INFOCOM 2007, pages

1199–1207, Barcelona, Spain.

Ni, M., Hu, M., Wang, Z., and Zhong, Z. (2015a). Packet re-

ception probability of vanets in urban intersecton sce-

nario. In Proc. Int. Conf. on Connected Vehicles and

Expo, pages 124–125, Shenzhen, China.

Ni, M., Pan, J., Cai, L., Yu, J., Wu, H., and Zhong, Z.

(2015b). Interference-based capacity analysis for ve-

hicular ad hoc networks. IEEE Communications Let-

ters, 19(4):621–624.

Steinmetz, E., Wildemeersch, M., Quek, T. Q. S., and

Wymeersch, H. (2015). A stochastic geometry model

for vehicular communication near intersections. In

2015 IEEE Globecom Workshops (GC Wkshps), pages

1–6.

Tong, Z., Lu, H., Haenggi, M., and Poellabauer, C. (2016).

A stochastic geometry approach to the modeling of

DSRC for vehicular safety communication. IEEE

Transactions on Intelligent Transportation Systems,

17(5):1448–1458.

Trivedi, K. S. (2008). Probability & statistics with reliabil-

ity, queuing and computer science applications. John

Wiley & Sons.

Yin, X., Ma, X., and Trivedi, K. S. (2013). An interact-

ing stochastic models approach for the performance

evaluation of DSRC vehicular safety communication.

IEEE Transactions on Computers, 62(5):873–885.

Zhao, J., Li, Z., Wang, Y., Wu, Z., Ma, X., and Zhao, Y.

(2020). An analytical framework for reliability eval-

uation of d-dimensional IEEE 802.11 broadcast wire-

less networks. Wireless Networks, 26:3373–3394.

Zhao, J., Wang, Y., Lu, H., Li, Z., and Ma, X. (2021a).

Interference-based qos and capacity analysis of vanets

for safety applications. IEEE Transactions on Vehicu-

lar Technology, 70(3):2448–2464.

Zhao, J., Zhou, H., Wang, Y., Lu, H., Li, Z., and Ma, X.

(2021b). Accelerating interference-based qos analysis

of vehicular ad hoc networks for bsm safety applica-

tions: Parallel numerical solutions and simulations. In

VEHITS, pages 600–610.

VEHITS 2025 - 11th International Conference on Vehicle Technology and Intelligent Transport Systems

528