Grid Interactive Smart Buildings Coordination in Multi-Area Power

Systems: A Delay-Robustness Analysis

Amedeo Andreotti

, Bianca Caiazzo

, Sara Leccese

, Alberto Petrillo

, Lorenzo Redi and

Stefania Santini

University of Naples Federico II, Italy

{amedeo.andreotti, bianca.caiazzo, sara.leccese, alberto.petrillo, lorenzo.redi, stefania.santini}@unina.it

Keywords:

Distributed Control, Grid-Interactive Smart Buildings, Delay Robustness, Frequency Regulation, Demand

Response.

Abstract:

This work focuses on the frequency support control problem for Grid-Interactive Smart Buildings (GISBs)

with Thermostatically-Controlled Loads (TCLs). The problem is formalized by leveraging multi-agent sys-

tems paradigm and a distributed delayed PID-based controller is introduced in order to guarantee that each

GISB provides a fast frequency support to the main grid while maintaining a desired comfort level. Compared

to the technical literature, the main novelty relies in considering communication latencies from the begin-

ning of control design phase, thus guaranteeing that the proposed control protocol is able to counteract the

unavoidable presence of heterogeneous time-varying delays arising during information sharing among all the

electrical entities. Extensive simulation results, exploiting also latin hypercube sampling technique, show the

effectiveness and the resilience of the approach with respect to delays and parameters uncertainties, while also

highlighting the delay stability margin of the entire network.

1 INTRODUCTION

The rapid integration of Renewable Energy Sources

(RESs), such as photovoltaic and wind power, has

signiﬁcantly changed the nature of power systems

(Wang et al., 2019b; Duan et al., 2022). Although

these greener resources promote a cleaner energy mix

(Xia et al., 2019), they have also introduced crucial

issues related to the stability of power systems. In-

deed, their inherently variable and unpredictable na-

ture can cause frequent and rapid power imbalances.

Moreover, the high level of RESs spread has also sig-

niﬁcantly reduced system inertia by replacing syn-

chronous machines (Zheng et al., 2021), thus increas-

ing both the amplitude and the recurrence of fre-

quency deviations (Zhao et al., 2023). It follows that,

despite their crucial beneﬁts devoted to greener and

cleaner energy systems, RESs may compromise the

overall grid reliability, thus requiring the need of ad-

hoc countermeasures. (Wang et al., 2019b).

https://orcid.org/0000-0002-6514-6807

https://orcid.org/0000-0002-1676-2814

https://orcid.org/0009-0001-8939-1129

https://orcid.org/0000-0003-4630-6673

https://orcid.org/0000-0002-0754-6271

Paving the way towards innovative and adaptive

strategies able to support frequency recovery while

ensuring the stability of modern power systems is

one of the fundamental issue to be addressed by re-

searchers in the next years. In this direction, there

is a growing interest into the usage of ﬂexible re-

sources from the demand side (Liu et al., 2022), such

as Temperature-Controlled Loads (TCLs), i.e., heat-

ing, ventilation and air-conditioning systems able to

quickly respond to power system variations (Xiao

et al., 2023). Unlike traditional demand response

systems, which often disrupt user activities, TCLs

can also provide grid support while maintaining at

the same time a proper comfort level by means of

predeﬁned temperature ranges. The recent trend

is the evaluation of collective effects provided by

a multiple aggregated TCLs, which leads to the

so-called Grid-Interactive Smart Buildings (GISBs)

paradigm. Speciﬁcally, GISBs represent an aggrega-

tion of TCLs, which can be viewed as one single en-

tity from grid perspective able to act as virtual energy

storage and provide timely support to frequency reg-

ulation (Wang et al., 2019b; Wang et al., 2019a).

Centralized solutions have been widely explored

to address coordination control problem of TCLs

(Zhang et al., 2018; Zhao et al., 2016). How-

Andreotti, A., Caiazzo, B., Leccese, S., Petrillo, A., Redi, L. and Santini, S.

Grid Interactive Smart Buildings Coordination in Multi-Area Power Systems: A Delay-Robustness Analysis.

DOI: 10.5220/0013357600003953

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2025), pages 48-55

ISBN: 978-989-758-751-1; ISSN: 2184-4968

ever, these architectures face some limitations, espe-

cially related to scalability issue and high computa-

tional burdens, which become more crucial as far as

the number of spatially distributed systems increases.

That’s way latest GISB control strategies are moving

towards distributed control solutions, which exploit

Multi-Agent Systems (MASs) modeling approach to

deal with the coordination of multiple TCLs. In

this perspective, each spatially distributed building

is modeled as an agent able to share its own lo-

cal information with the corresponding neighboring

set by means of a communication network in order

to achieve a global coordinated behavior (Ge et al.,

2018). Along this line, a distributed average con-

sensus algorithm has been introduced in (Chen et al.,

2014) to solve the fair power allocation problem in

a TLC aggregator. Authors in (Zheng et al., 2021)

have proposed a distributed control approach for fre-

quency support in aggregated buildings able to bal-

ance their energy level while guaranteeing robust and

reliable operations with a desired comfort level for

the occupants. Moreover, in (Wang et al., 2019a) a

two-layer distributed control protocol accounting for

both the inner and the inter buildings communication

graphs has been designed. Furthermore, in (Wang

et al., 2019b), by the means of double layer control

protocols, authors achieve both fair power allocation

among GISBs and a proper comfort level among all

available TCLs. These control objectives are fulﬁlled

by means of a distributed sliding mode controller,

which provides also robustness and fast response un-

der varying conditions.

Besides the beneﬁts of distributed control ap-

proaches, the control over communication networks

poses several challenges. Since the information ex-

change among buildings is realized via a wireless

communication network, random delays usually arise.

In this context, each GISB receives information with

different time-varying delays, whose value depends

on the network conditions and the speciﬁc commu-

nication channel. It follows that delays may signiﬁ-

cantly affect the aggregator control performance and

compromise frequency support capability. Further-

more, in the worst case, delays may lead to the in-

stability of the overall network (Caiazzo et al., 2022).

Based on the above, one can conclude that delays

should be considered from the beginning in order

to prevent dangerous and undesirable situations, i.e.,

from the control design phase. This implies that the

distributed controller has to be designed and imple-

mented via outdated information, which can be done

by using the time stamp inserted into messages to cor-

rectly correlate the information.

Based on the these considerations, this article

aims at designing a distributed controller for the co-

ordination of a GISBs aggregator able to provide fast

frequency support to the grid in normal operating con-

ditions despite the presence of unavoidable communi-

cation delays. We would like to highlight that, com-

pared with (Wang et al., 2019b), where the simula-

tion campaign has also involved a robustness analy-

sis with respect to constant and homogeneous com-

munication delay, here we allow delays to be time-

varying and heterogeneous for each electrical entity

within the network, while considering them from the

control design phase. We carry out an extensive sim-

ulation campaign in order to derive the delay stability

margin, i.e., the maximum tolerable delay preserving

the stability of the the overall power system. More-

over, to further conﬁrm the effectiveness of the pro-

posed approach, we also employ the Latin Hypercube

Sampling (LHS) method to assess the control perfor-

mance under several parameters and communication

delays uncertainties/variations, as well as for all the

possible combinations of them.

Finally, the paper structure is given as follows.

In Section 2 the problem statement is detailed along

with the modeling of the multi-area power system.

The distributed control protocol for frequency sup-

port problem with heterogeneous time-varying delays

is presented in Section 3, while simulation results are

reported in Section 4. Conclusions are drawn in Sec-

tion 5.

2 PROBLEM FORMULATION

Consider a multi-area power system composed by

M control areas physically interconnected through

tie-lines. Each area k (k = 1, ··· , M) consists of

variable local loads and N

GISBs. These latter

are equipped with only air conditioning systems and

share their temperature information with the corre-

sponding neighboring GISBs via a wireless commu-

nication network subject to communication impair-

ments. Thus, the N

GISBs in the k-the area act as

a single aggregator for the fast frequency support of

the multi-area power system.

Inspired by (Wang et al., 2019b), the aim of this

work is to design a novel distributed controller for

the GISBs able to guarantee that the whole aggre-

gator provides a fast frequency support to the main

grid −while maintaining its temperature within user-

deﬁned ranges− despite the presence of communica-

tion latencies.

In the sequel we ﬁrstly provide the modeling of the

multi-area power system we consider herein.

Grid Interactive Smart Buildings Coordination in Multi-Area Power Systems: A Delay-Robustness Analysis

2.1 Network Modeling

The communication among GISBs into the k-the con-

trol area can be modeled as a directed graph G

, E

, A

}, where V

is the set of the N

GISBs

and E

⊆ V

× V

stands for the edges set describ-

ing the active communication links. Matrix A

i j

] ∈ R

×N

is the adjacency matrix, whose ele-

ments are a

i j

= 1 if there exists a link between the

i-th and j-th GISBs, 0 otherwise. Associated to

this graph there is the Laplacian matrix L

= [l

i j

] ∈

×N

such that l

∑

j=1

i j

and l

i j

= −a

i j

, j ̸= i.

Since we assume also the presence of a virtual build-

ing into the cyber-space imposing the reference be-

havior to the speciﬁc k-th control area, it results an

augmented directed graph G

with a Pinning ma-

trix P

= diag{p

, p

, . . . , p

}, whose elements are

such that p

= 1 if the leader GISB is directly con-

nected to the i-th GISB, p

= 0 otherwise. Finally,

the set of neighbors of the i-th GISB is deﬁned as

i,k

= { j : (i, j) ∈ E

The overall electric topology of the multi-area power

system can be also modeled as a connected weighted

graph G

= {V

, E

, T }, where V

is the set of

electrical buses connecting the different control areas,

while E

represents the set of electric power lines.

Furthermore, T is the associated weighted adjacency

matrix, whose elements are such that T

k,ι

= 1 if and

only if there is a tie-line between the area k and area

ι, T

k,ι

= 0 otherwise, for any k, ι ∈ {1, ·· · , M}.

2.2 Multi-Area Power System Model

Here we ﬁrstly detail the model of the entire multi-

area power system by means of Load Frequency Con-

trol (LFC) and, then, we move towards the description

of the single GISBs dynamics.

2.2.1 Load Frequency Control

The stability of the overall power system is ensured

via LFC (Wadi et al., 2024), whose objective is to

guarantee that the frequency deviations remain within

an allowable ranges, despite the presence of addi-

tional loads (Yousef et al., 2014). The typical LFC

structure within the single area, reported in Figure

1, allows the physical connection with other differ-

ent control areas, thus automatically balancing and

sharing the load among them. Beside the LFC, we

assume that the power output of the generators is

controlled by their primary and secondary controllers

(Wang et al., 2019b). The relation between power

mismatch and frequency deviation into the k-th area

can be modeled as

∆ f

(s) =

s + D

−∆P

(s) + ∆P

RES

(s)

+ M

(s)



∆P

(s) −

∆ f

(s)



− ∆P

tie

(s) + ∆P

agg

(s)

(1)

where ∆ f

is the frequency deviation in the k-th con-

trol area, H

and D

are the load damping and the in-

ertia of the system, respectively, while R

stands for

the speed droop coefﬁcient. Furthermore, ∆P

is the

secondary control input, while ∆P

, ∆P

RES

, ∆P

tie

and

∆P

agg

are the power variations of loads, RESs, tie-line

and GISBs aggregator, respectively. M

denotes the

generators dynamics, which can be expressed as

(s) =

1 + sT

, (2)

where T

and T

are the time constants of the gener-

ator and turbine, respectively, while T

and T

are

the time constants of the transient droop compensator

(Wang et al., 2019b).

The power transfer between the k-th and the ι-th con-

trol areas, k, ι, ∈ {1, . . . , M}, is computed as

∆P

tie

(s) =

2π

∑

ι=1

kι

(∆ f

(s) − ∆ f

(s)

. (3)

According to the technical literature (Wu et al., 2017),

the secondary control input ∆P

in (1) is usually de-

signed as a PI controller weighing the current value

of the Area Control Error (ACE), whose expression is

derived as

ACE

(s) = B

∆ f

(s) + ∆P

tie

(s), (4)

where B

is the frequency bias factor of the k-th con-

trol area. Hence, by deﬁning K

and K

as the pro-

portional and integral gains respectively, the PI-based

secondary controller is provided as follows:

∆P

(s) =





ACE

(s). (5)

However, fast frequency recovery cannot be ensured

by means of the solely secondary control input (5)

(Wang et al., 2019b). Hence, our aim is to adjust the

value of the total power required by the smart build-

ings aggregator, i.e., ∆P

agg

(s) in (1), so to make the

frequency recovery faster, which is not possible by

means of (5).

SMARTGREENS 2025 - 14th International Conference on Smart Cities and Green ICT Systems

















 







 





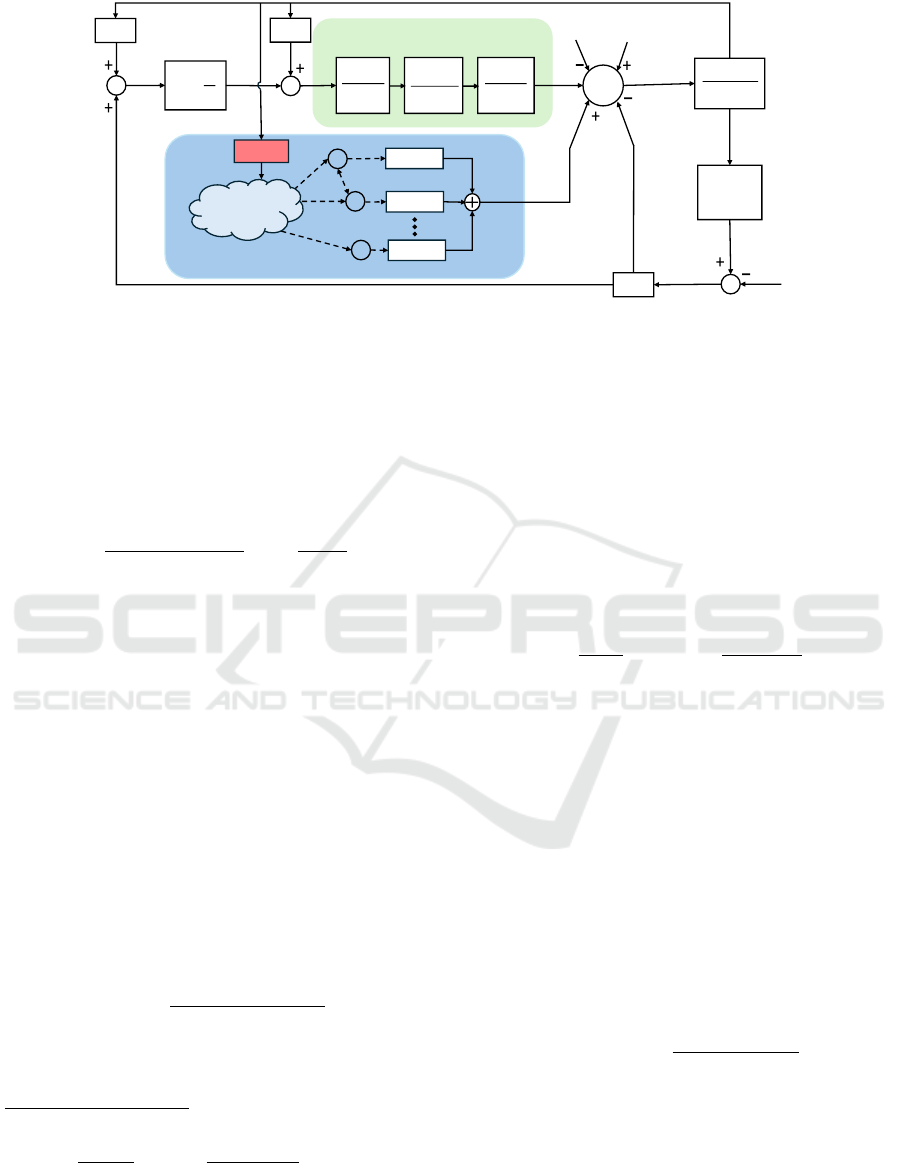
Generator Model

 





 





















































































GIBS#1

GIBS#2

GIBS#N

Smart Building Aggregator





GIBS#0

Communication

Network

Figure 1: Overview of the LFC scheme of the k-th area.

2.2.2 Smart Buildings Thermal Dynamic Model

Through this work we assume the i-th smart building

into the k-th area to be equipped with only TCLs, thus

implying that its dynamical behavior can be modeled

by means of its average temperature, i.e., (Wang et al.,

2019b):

i,k

(t) =

amb,k

(t) − θ

i,k

(t)

i,k

− η

i,k

(t)

i,k

+ ω

i,k

(t),

(6)

where θ

i,k

(t) and θ

amb,k

(t) are the internal and am-

bient temperatures, C

i,k

and R

i,k

are the thermal ca-

pacitance and resistance, respectively, λ

i,k

is the num-

ber of TCLs in the i-th building, p

i,k

(t) represents the

power consumption. Furthermore, η

i,k

is the thermal

coefﬁcient which is deﬁned as η

i,k

> 0 for cooling

TLC and η

i,k

≤ 0 for heating ones. Finally, ω

i,k

(t)

represents a Gaussian disturbance with zero means.

However, in practical applications a GISB has to keep

its temperature within a user-deﬁned range, which

may differ between different buildings. Hence, by

deﬁning this temperature range as [

i,k

− ∆θ

i,k

∆θ

i,k

], with

i,k

and ∆θ

i,k

the set-point temperature

and its admissible tolerance, we can introduce an ad-

ditional variable ε

i,k

(t) ∈ [0, 1] standing for the com-

fort level index, i.e.:

i,k

(t) =

i,k

(t) −

i,k

+ ∆θ

i,k

2∆θ

i,k

. (7)

Then, by substituting this latter into (6) and

deﬁning the time-varying disturbance d

i,k

(t) =

amb,k

(t)−

i,k

+∆θ

i,k

2∆θ

i,k

, we obtain:

i,k

(t) =

i,k

(t) −

i,k

2∆θ

i,k

(t) + d

i,k

(t).

(8)

Note that, the comfort level reﬂects the thermal power

of the i-th building. Speciﬁcally, whenever the i-th

GISB reaches its maximum allowable temperature,

then ε

i,k

(t) = 1, meaning that the cooling capacity of

its own TLC cannot be further reduced. On the other

hand, if the comfort level of the i-th GISB is such that

i,k

(t) = 0, it means that it is working at its minimum

allowable temperature and, hence, its cooling capac-

ity cannot be further increased (Wang et al., 2019b).

Following (Wang et al., 2019b), we introduce an aux-

iliary state variable ζ

i,k

(t), whose expression is given

as follows:

i,k

(t) = a

i,k

(t) + b

i,k

(t) + d

i,k

(t), (9)

being a

i,k

and b

i,k

2∆θ

i,k

. Then, the

comfort level dynamics of the i-th building can be re-

cast as a control-oriented state-space model, i.e.:

˙x

i,k

(t) = A

i,k

(t) + B

i,k

(t) + d

i,k

(t)), (10)

where x

i,k

(t) = [ε

i,k

(t), ζ

i,k

(t)]

⊤

, u

i,k

(t) = ˙p

i,k

(t) is the

distributed control input to be designed, while A

i,k

and

i,k

are deﬁned as:

i,k



0 1

0 a

i,k



, B

i,k



i,k



. (11)

The amount of power that each building within

the aggregator has to consume to maintain its com-

fort level at a constant reference value

0,k

is deﬁned

as baseline power p

b,i

(t), which can be computed as

b,i

(t) = lim

t→∞

−a

i,k

− d

i,k

(t)

i,k

. (12)

Thus, the baseline power of the k-th GISBs aggregator

is P

(t) =

∑

i=1

b,i

(t), k ∈ {1, . . . , M}.

Remark 1. Similar to an energy storage system with

dissipation, a GISB maintains its desired temperature

while operating at baseline power. Indeed, when its

power consumption is less then the baseline P

(t), it

injects power (i.e., discharges) into the grid, whereas

Grid Interactive Smart Buildings Coordination in Multi-Area Power Systems: A Delay-Robustness Analysis

whenever its power consumption increases w.r.t. the

baseline, it is able to absorb power (i.e., charge) from

the grid (Wang et al., 2019b). Hence, by controlling

the GISBs aggregator power consumption, i.e. the ref-

erence comfort level, the frequency deviation of the

k-th area can be stabilized.

The control problem addressed through this

manuscript can be formulated as follows.

Problem 1. Consider an energy community of M con-

trol areas physically interconnected via tie-lines, each

of them composed of N

k+1

GISBs sharing informa-

tion via a communication network. Design a dis-

tributed control law able to ensure that all GISBs

within the k-th area, k ∈ {1, . . . , M}, are able to track

the reference behaviour imposed by the correspond-

ing leader x

0,k

(t) = [ε

0,k

(t), ζ

0,k

(t)]

⊤

. This problem

can be mathematically recast as a leader-tracking

consensus, whose control objective is to ﬁnd u

i,k

(t)

in (10) such that, ∀i = 1, ··· , N

lim

t→∞

∥x

0,k

(t) − x

i,k

(t)∥ = 0, k ∈ {1, . . . , M}, (13)

despite the presence of unavoidable communications

delays.

3 DISTRIBUTED FREQUENCY

SUPPORT CONTROL WITH

HETEROGENEOUS

TIME-VARYING DELAYS

Before presenting the distributed control protocol we

propose through this work, we ﬁrstly detail the leader

behavior within each control area according to the

technical literature (Wang et al., 2019b).

3.1 Leader Control

To solve Problem 1, we assume that, in each area k,

the reference comfort level is provided by a virtual

GISB, labeled with index 0, i.e., x

0,k

(t), whose be-

havior is derived according to (Wang et al., 2019b).

Speciﬁcally, based on grid frequency conditions, it

operates in two distinct modes, i.e., i) Frequency Sup-

port Mode (FSM) and ii) Comfort Recovery Mode

(CRM). For sake of clarity, in what follows we pro-

vide a description of both operating modalities.

Frequency Support Mode. FSM is activated when-

ever the system frequency deviations exceed a pre-

deﬁned threshold which denotes a critical imbalance

between power generation and consumption. Under

these conditions, the k-th GISB aggregator provides a

primary frequency support by dynamically adjusting

its power consumption, which can be computed as

(t) =

∑

i=1

i,k

(t)

(

(t) + R

agg,k

(∆ f

− ∆ f

(t)), ∆ f

≥ ∆ f

(t) + R

agg,k

(∆ f

− ∆ f

(t)), ∆ f

≤ ∆ f

(14)

where R

agg,k

is the droop gain of the k-th GISB ag-

gregator, while ∆ f

and ∆ f

stand for the maximum

and the minimum acceptable frequency values. These

latter are usually equal to ∆ f

= 0.1 [Hz] and ∆ f

−0.1[Hz] (Wadi et al., 2024). By virtue of (14), the k-

th leader is able to discharge (charge) power to (from)

the grid during frequency drops (surpluses). In this

operational mode, based on (9) and (14), the behavior

of the k-th leader is described as follows:

(

0,k

(t) =

0,k

(t)dt

0,k

(t) =

∑

i=1

i,k

(t)+

∑

i=1

i,k

(t)+d

i,k

(t)]

, ∀k.

(15)

Comfort Recovery Mode. We say that the k-th

GISBs aggregator operates in CRM mode whenever

∆ f

∈ [∆ f

, ∆ f

]. In this case, the temperature of

each smart building involved into the single area con-

trol is kept at a certain value and, hence, the whole

aggregator absorbs an amount of power that is P

(t).

Thus, the leader behavior x

0,k

(t) = cost with ε

0,k

(t) =

0,k

and ζ

0,k

(t) = 0.

Based on these two operational modes, we ﬁnish-

up into a double-layer control architecture for each

control area as in (Wang et al., 2019b), with the ﬁrst

layer provided by the leader behavior and the second

layer to be designed to satisfy objective (13) in Prob-

lem 1.

3.2 Cooperative Control Protocol for

the GIBS

Here, the objective is to handle Problem 1 arising

in each control area, i.e., to guarantee that all GISB

within the k-th area, k ∈ {1, . . . , M}, track the cor-

responding leader behavior x

0,k

(t). Furthermore, the

distributed control strategy we aim to design has to

counteract the presence of time-varying communica-

tion delays arising during information sharing pro-

cess. For each building i, i = 1, ··· , N

, k = 1, . . . , M,

we ﬁrstly deﬁne the error with respect to the corre-

sponding leader as:

i,k

(t) =



ε,i,k

(t)

ζ,i,k

(t)





i,k

(t) − ε

0,k

(t)

i,k

(t) − ζ

0,k

(t)



. (16)

To deal with Problem 1 we propose the follow-

ing distributed networked PID-based delayed control

SMARTGREENS 2025 - 14th International Conference on Smart Cities and Green ICT Systems

strategy:

i,k

(t, τ

i,k

(t)) =

∑

j∈N

i j

i,k

(t − τ

i,k

(t)) − e

j,k

(t − τ

i,k

(t)))

∑

j∈N

i j

( ˙e

i,k

(t − τ

i,k

(t)) − ˙e

j,k

(t − τ

i,k

(t))),

∑

j∈N

i j

i,k

(s − τ

i,k

(s)) − e

j,k

(s − τ

i,k

(s)))ds,

(17)

where k

, k

are the proportional, derivative and

integral control gains, respectively, while a

i j

mod-

els the communication network topology into the k-th

control area emerging from the presence/absence of

the communication link between i-th and j-th GISB

(see Section 2.1). Furthermore, τ

i j

(t) represents the

communication time-varying delays between the i-th

and j-th GISB, for all i, j ∈ V

, which is assumed to

be detectable by timestamp. In doing so, (17) is com-

puted via outdated information, thus preventing any

instability phenomena (Caiazzo et al., 2022).

Assumption 1. (Andreotti et al., 2021) Time-varying

time-delays signals τ

i j

(t) are bounded and slowly-

varying, i.e., τ

i j

(t) ≤ τ

⋆

and

i j

(t) ≤ µ < 1, ∀i, j ∈

, ∀k ∈ {1, · ·· , M}.

Remark 2. The stability of the (10) under the ac-

tion of (17) can be proved by means of Lyapunov-

Krasovskii theory for time-delay systems (see, e.g.,

(Andreotti et al., 2021)).

4 NUMERICAL ANALYSIS

In this section we validate the effectiveness of the pro-

posed control (17) in coordinating GISBs aggrega-

tor for fast frequency support despite the presence of

heterogeneous time-varying communication delays.

To this aim, we leverage MATLAB/Simulink simu-

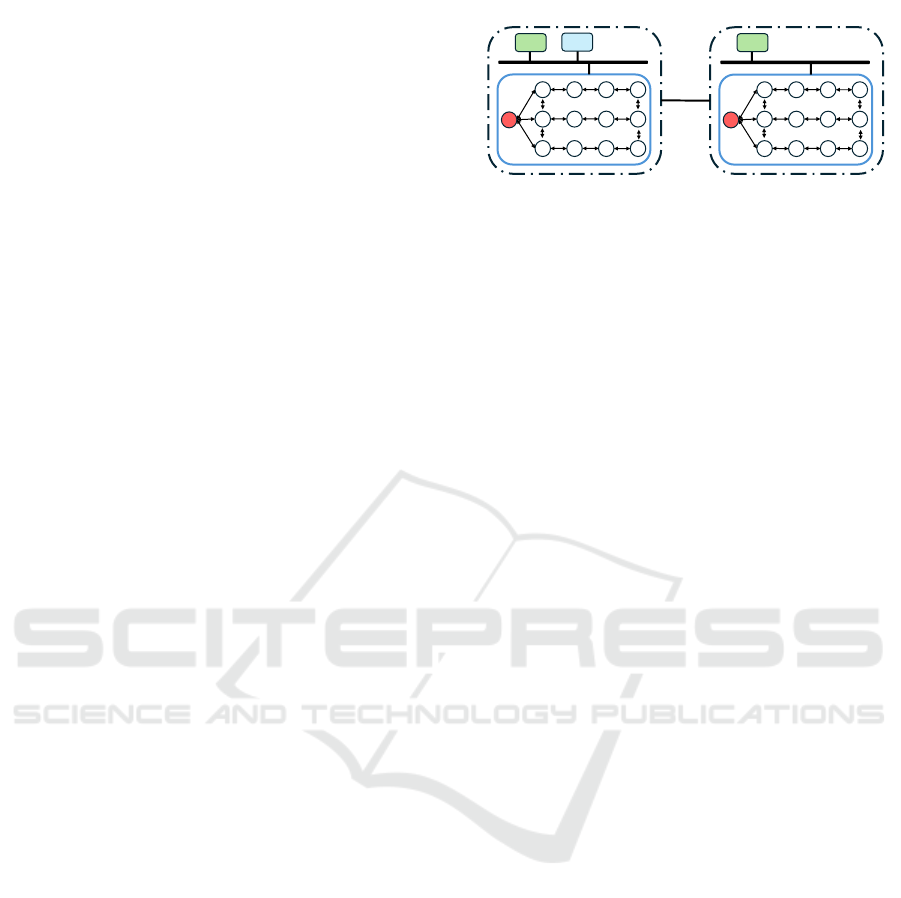
lation platform to emulate a multi-area power system

consisting of M = 2 control areas, each of them in-

cluding an aggregator of N

= 12 buildings, k = 1, 2.

Without loss of generality, the LFC parameters in

(1) are assumed to be equal in both control areas

and all the buildings have the same physical char-

acteristics. Communication and electrical topologies

are chosen according to Figure 2, while multi-area

system parameters are chosen according to (Wang

et al., 2019b). From these latter, we have a

i,k

−0.25, b

i,k

= −3.125 × 10

−3

, d

i,k

= 0.5625, λ

i,k

100, for all i ∈ V

, k = 1, 2. The initial reference

comfort level in each control area provided by the

corresponding virtual GISB during CRM is set as

1 2 3 4

8 7 6 5

9 10 11 12

LOAD

GEN

1 2 3 4

8 7 6 5

9 10 11 12

GEN

Tie Line

1-2

AREA #1

AREA #2

Figure 2: Communication and electrical topologies of 2-

Area power System.

0,k

(0) =

= 50%, while the ambient temperature

is θ

amb,k

= 30[

◦

C], k = 1, 2. This allows computing

the baseline power according to (12), thus obtaining

i,b

(t) = 1.68 [MW]. A time interval of t = 150 [s] is

considered for validation purpose, where at t = 96 [s]

a load increment of 1.5 [MW] emulates the occurrence

of a contingency within Area #1. In what follows, we

ﬁrstly present the worst case scenario, where the max-

imum delay τ

⋆

is chosen as the delay stability mar-

gin preserving the stability. Then, the LHS approach

(Helton and Davis, 2003) is exploited to evaluate the

resilience of the controller (17) w.r.t. different τ

⋆

and

uncertainty range of GISB parameters.

4.1 Worst Case Scenario

In this section we evaluate the robustness of the pro-

posed distributed control in presence of network la-

tencies both in Area #1 and Area #2. The objective is

to ﬁnd the delay stability margin of the overall system,

i.e., the maximum admissible delay able to preserve

the stability of the entire power system.

To this aim, we carried-out a simulation campaign

where the heterogeneous time-varying delays τ

i j

are

emulated as uniformly random variables with a max-

imum value τ

⋆

, which has been iteratively increased

till the stability of the network has been violated. Our

simulation campaign has revealed that the stability of

the multi-area power system we consider is preserved

till τ

⋆

= 0.2 [s], which hence represents our delay sta-

bility margin.

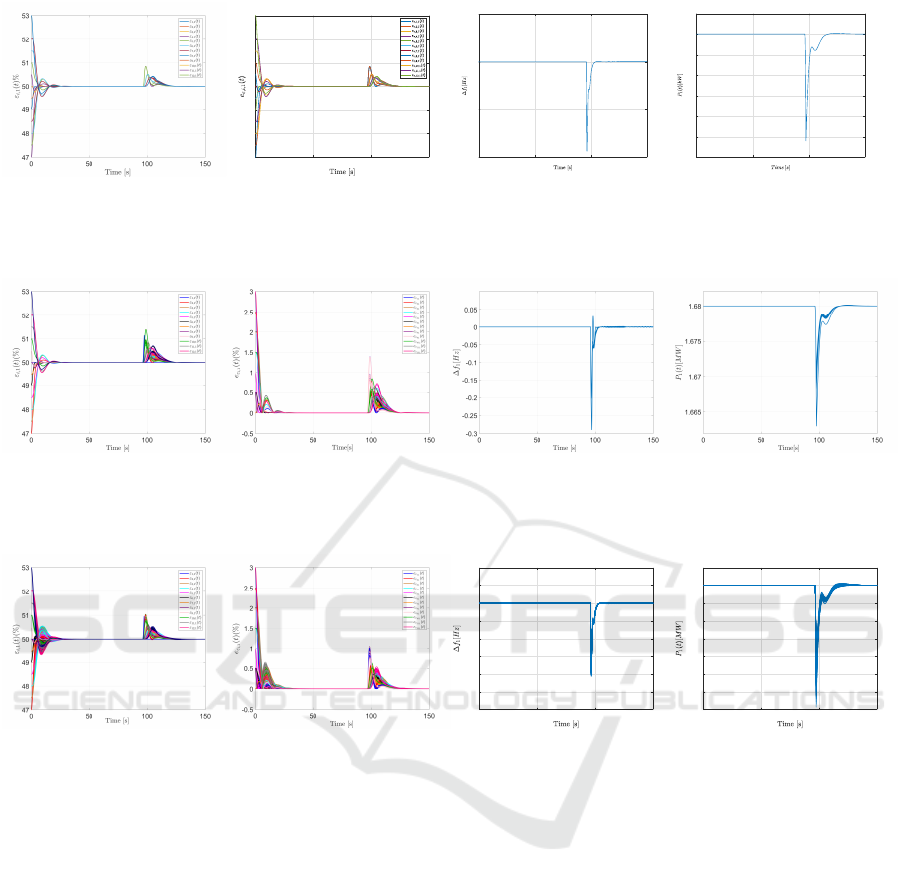
Simulation results achieved in Area #1 in this

worst case scenario are reported in Figure 3. Speciﬁ-

cally, from Figure 3(a) it is possible to appreciate that

our distributed control is able to perform the comfort

recovery of all the GISBs, also after the load chang-

ing occurring at t = 96 [s], with small bounded er-

rors during the transient phases (see Figure 3(b)). In-

deed, at this time instant ∆ f

exceeds the minimum

threshold (see Figure 3(c)) and, then, leader behavior

switches to FSM mode according to (14). Then, from

t ∈ [96, 120] [s], the aggregator #1 operates below its

baseline power (see Figure 4(d)), thus discharging

into the grid for primary frequency support. Similar

Grid Interactive Smart Buildings Coordination in Multi-Area Power Systems: A Delay-Robustness Analysis

(a)

0 50 100 150

-3

-2

-1

(b)

0 50 100 150

-0.2

-0.1

0.1

(c)

0 50 100 150

1668

1670

1672

1674

1676

1678

1680

1682

(d)

Figure 3: Distributed frequency support control with heterogeneous time-varying delays with τ

⋆

= 0.2[s]. Time-history of: a)

i,1

(t)[%], i ∈ V

; b) e

ε,i,1

(t)[%], i ∈ V

; c) ∆ f

(t)[Hz]; d) P

(t) [kW].

(a) (b) (c) (d)

Figure 4: Resilience analysis via LHS method in uncertain delays conditions with τ

⋆

= 0.1[s]. Time-history of: a)

i,1

(t)[%], i ∈ V

; b) e

ε,i,1

(t)[%], i ∈ V

; c) ∆ f

(t)[Hz]; d) P

(t) [MW ].

(a) (b)

0 50 100 150

-0.3

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

(c)

0 50 100 150

1.666

1.668

1.67

1.672

1.674

1.676

1.678

1.68

1.682

(d)

Figure 5: Resilience analysis via LHS method in uncertain GISBs parameters conditions with τ

⋆

= 0.1[s]. Time-history of:

a) ε

i,1

(t)[%], i ∈ V

; b) e

ε,i,1

(t)[%], i ∈ V

; c) ∆ f

(t)[Hz]; d) P

(t) [MW ].

results are obtained for the Area #2 and, hence, they

are omitted for the sake of brevity.

4.2 Resilience via Latin Hypercube

Sampling Approach

Here we evaluate the robustness and the resilience

of the proposed methodology w.r.t. delay variations

as well as GISBs parameters uncertainties in both

areas. Speciﬁcally, we consider two different sce-

narios: a) GISBs parameters assume their nominal

values, while delays variations are considered, i.e.,

i j

(t) ∈ [−30%τ

⋆

, +30%τ

⋆

] with τ

⋆

= 0.1 [s]; b) no

delays variations are taken into account, while GISBs

parameters uncertainties are emulated, i.e., the coefﬁ-

cients of the matrices A

i,k

and B

i,k

in (11) vary within

the range [−20%, +20%] with respect to their nomi-

nal values. To this aim, the LHS approach is exploited

to conﬁrm the resilience of the proposed control strat-

egy under GISB uncertainties and variable commu-

nication time-delays, as well as for all the possible

combinations of them. In both cases, we carried-out a

number of simulations equal to 50.

Results of the two cases a) and b) are reported in

Figures 4-5, which conﬁrm the resilience of the dis-

tributed delayed controller (17) also in these uncertain

conditions.

5 CONCLUSIONS

The paper has addressed the problem of frequency

support for Grid-Interactive Smart Buildings (GISBs)

with Thermostatically-Controlled Loads (TCLs). A

distributed delayed controller has been devised in or-

SMARTGREENS 2025 - 14th International Conference on Smart Cities and Green ICT Systems

der to ensure that each GISB provides a fast frequency

support, while counteracting the presence of commu-

nication delays. The delay stability margin has been

found by means of an extensive simulation campaign,

which has also exploited the latin hypercube sampling

technique to prove the resilience of the proposed con-

troller with respect to parameters and delays uncer-

tainties.

REFERENCES

Andreotti, A., Caiazzo, B., Petrillo, A., and Santini,

S. (2021). Distributed robust ﬁnite-time secondary

control for stand-alone microgrids with time-varying

communication delays. IEEE Access, 9:59548–

59563.

Caiazzo, B., Lui, D. G., Petrillo, A., and Santini, S. (2022).

Cooperative ﬁnite-time control for autonomous ve-

hicles platoons with nonuniform v2v communication

delays. IFAC-PapersOnLine, 55(36):145–150.

Chen, C., Wang, J., and Kishore, S. (2014). A distributed

direct load control approach for large-scale residential

demand response. IEEE Transactions on Power Sys-

tems, 29(5):2219–2228.

Duan, Q., Zeng, K., Liu, J., Du, B., and Liao, P. (2022). Ag-

gregated control of smart building units for frequency

regulation in multi-region power systems. In 2022 7th

Asia Conference on Power and Electrical Engineering

(ACPEE), pages 1209–1214. IEEE.

Ge, X., Han, Q.-L., Ding, D., Zhang, X.-M., and Ning, B.

(2018). A survey on recent advances in distributed

sampled-data cooperative control of multi-agent sys-

tems. Neurocomputing, 275:1684–1701.

Helton, J. C. and Davis, F. J. (2003). Latin hypercube sam-

pling and the propagation of uncertainty in analyses

of complex systems. Reliability Engineering & Sys-

tem Safety, 81(1):23–69.

Liu, X., Li, Y., Lin, X., Guo, J., Shi, Y., and Shen, Y. (2022).

Dynamic bidding strategy for a demand response ag-

gregator in the frequency regulation market. Applied

Energy, 314:118998.

Wadi, M., Shobole, A., Elmasry, W., and Kucuk, I. (2024).

Load frequency control in smart grids: A review of

recent developments. Renewable and Sustainable En-

ergy Reviews, 189:114013.

Wang, Y., Tang, Y., Xu, Y., and Xu, Y. (2019a). A dis-

tributed control scheme of thermostatically controlled

loads for the building-microgrid community. IEEE

Transactions on Sustainable Energy, 11(1):350–360.

Wang, Y., Xu, Y., and Tang, Y. (2019b). Distributed ag-

gregation control of grid-interactive smart buildings

for power system frequency support. Applied energy,

251:113371.

Wu, Y., Wei, Z., Weng, J., Li, X., and Deng, R. H. (2017).

Resonance attacks on load frequency control of smart

grids. IEEE Transactions on Smart Grid, 9(5):4490–

4502.

Xia, M., Song, Y., and Chen, Q. (2019). Hierarchical con-

trol of thermostatically controlled loads oriented smart

buildings. Applied energy, 254:113493.

Xiao, H., Zhang, M., Zeng, L., Wu, G., Wu, C., and Wu,

C. (2023). Hierarchical control strategy of thermo-

statically controlled load considering multiple factors.

Energy and Buildings, 291:113148.

Yousef, H. A., Khalfan, A.-K., Albadi, M. H., and Hossein-

zadeh, N. (2014). Load frequency control of a multi-

area power system: An adaptive fuzzy logic approach.

IEEE transactions on power systems, 29(4):1822–

1830.

Zhang, C., Xu, Y., Li, Z., and Dong, Z. Y. (2018). Ro-

bustly coordinated operation of a multi-energy micro-

grid with ﬂexible electric and thermal loads. IEEE

Transactions on Smart Grid, 10(3):2765–2775.

Zhao, H., Wu, Q., Huang, S., Zhang, H., Liu, Y., and Xue,

Y. (2016). Hierarchical control of thermostatically

controlled loads for primary frequency support. IEEE

Transactions on Smart Grid, 9(4):2986–2998.

Zhao, N., Yue, D., Dou, C., and Shi, T. (2023). Distributed

dynamic event-triggered cooperative control of mul-

tiple tcls and hess for improving frequency regula-

tion. IEEE Transactions on Industrial Informatics,

20(2):1539–1549.

Zheng, L., An, Z., Xia, Q., Kandula, R. P., Saeedifard, M.,

Divan, D., Grijalva, S., and Abdallah, C. T. (2021).

Distributed control of aggregated smart buildings for

frequency regulation. In 2021 IEEE Industry Applica-

tions Society Annual Meeting (IAS), pages 1–8. IEEE.

Grid Interactive Smart Buildings Coordination in Multi-Area Power Systems: A Delay-Robustness Analysis