An Engineer-Friendly Terminology of White, Black and

Grey-Box Models

Eugen Boos

1,*

, Mauritz Mälzer

, Felix Conrad

, Hajo Wiemer

and Steffen Ihlenfeldt

1,2

Institute of Mechatronic Engineering, Technische Universität Dresden, Germany

Fraunhofer Institute for Machine Tools and Forming Technology, Chemnitz, Germany

Keywords: Modeling, White-Box, Black-Box, Grey-Box, Taxonomy, Usable AI, Explainable AI.

Abstract: In engineering modeling, white-box and black-box concepts represent two fundamental approaches for

modeling systems. White-box models rely on detailed prior knowledge of the physical system, enabling

transparent and explainable representations. Black-box models, on the other hand, consist of opaque internal

workings and decision-making processes that prevent immediate interpretability. They are mainly data-driven,

relying on statistical methods to capture system behavior. Depending on the literature at hand, the exact

definitions of these two approaches differ. With the continuous emergence of machine learning algorithms in

engineering and their move towards enhanced explainability and usability, the exact definition and assignment

of white- and black-box properties soften. Grey-box modeling provides a hybrid approach. However, this

term, as widely as it is used, has no clear definition either. This paper proposes a novel model on the relation

of white-, black- and grey-box modeling, offering an improved categorization of conventional vanilla models,

state-of-the-art hybrid models as well as the derivation of recommendations for action for targeted model

improvement.

1 INTRODUCTION

Modeling of engineering and industrial processes is

traditionally based on two primary approaches:

white-box and black-box modeling. While white-box

modeling involves constructing models based on

established physical relations and deterministic

equations, focusing the model making based on prior

knowledge. Black-box modeling, in contrast, utilizes

parametric models calibrated to real world data

obtained from the process, focusing on experimental

data as the main information source. Opposed to

using only one single source of knowledge, the idea

of grey-box identification is to utilize both: prior

knowledge and experimental data. Therefore, they are

combining the strengths of the two approaches.

(Bohlin 2006)

This general definition is widely used to classify

different models. However, with the continuous rise

of machine learning methods, especially deep neural

networks, the boundaries of this traditional definition

move from the source of knowledge to the aspect of

explainability and transparency (Pintelas, Livieris,

Corresponding Author

and Pintelas 2020). The internal workings and the

reasoning of the model’s decision making are

becoming more decisive for the subdivision between

white- and black-model than the source of knowledge

(Shakerin and Gupta 2020). This shift can be observed

due to the presumed change of perspective from the

development of a model to the comprehensible

industrial application of it. One definition is based on

how a model is created, and the other is based on the

requirements the model must meet to be usable

(Wiemer et al. 2023).

A notable trend has emerged favoring a shift from

black-box models towards white-box models,

particularly in decision critical sectors such as

healthcare, finance, and the military. This shift

emphasizes the development of transparent white-

box models and the integration of white- and black-

box approaches to ensure that the outcomes produced

by these models can be effectively explained to the

person in charge (Rudin 2019). Nevertheless, this

trend is focused solely on the explainability of the

model, not the source of information (Loyola-

González 2019).

Boos, E., Mälzer, M., Conrad, F., Wiemer, H. and Ihlenfeldt, S.

An Engineer-Friendly Terminology of White, Black and Grey-Box Models.

DOI: 10.5220/0013361400003896

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Model-Based Software and Systems Engineering (MODELSWARD 2025), pages 313-320

ISBN: 978-989-758-729-0; ISSN: 2184-4348

313

The opposite trend can be observed as well. With

the continuous growth of computational power, the

complexity of physical simulations has seen a

correlating growth (Mittal and Tolk 2019), leading to

white-box models, which are based on prior

knowledge, but still lack usable explainability due to

their level of complexity.

This paradigm shift has profound implications for

the way models are selected, developed and deployed

in engineering and industrial contexts. As

explainability and transparency gain prominence,

models that were traditionally classified as white-box

or black-box are increasingly reevaluated based on

their ability to provide interpretable and actionable

insights. Traditional white-box models, while rooted

in physical principles and prior knowledge, may

become opaque when their complexity increases,

reducing their usability in practical applications.

Conversely, black-box models, such as deep neural

networks, often deliver high predictive accuracy but

struggle to meet the growing demand for

explainability in critical decision-making

environments.

This evolving landscape underscores the necessity

of hybrid approaches, such as grey-box models, which

aim to balance the transparency of white-box methods

with the adaptability and data-driven nature of black-

box models. However, as the defining boundaries

between white- and black-box models shift, the clear

affiliation of different types of grey-box models get

fuzzy and the categorization becomes increasingly

ambiguous.

The increasing ambiguity in categorizing grey-

box models necessitates a refined framework to

balance interpretability and complexity

systematically. As hybrid approaches blur the lines

between white-box and black-box paradigms, a

nuanced classification helps guide model selection

and deployment. Such a framework provides a

structured way to evaluate trade-offs, enhancing

decision-making and fostering trust in machine

learning systems. It also encourages innovation by

identifying opportunities for developing models that

better integrate certain properties. Ultimately, higher

clarity enhances communication and alignment in

model developing.

2 MODELING

2.1 General Approach to Modeling

Regardless of the evadable “color” of a “box”, Ljung

(Ljung 1996) separates the creation of a model into

two distinguishable phases: modeling, specifying the

class of the model; and fitting, specifying the internal

model parameters to data.

Since both the model class specification and the

fitting process are executed algorithmically, they can

be represented as the following functions:

𝑀



𝑥



,𝑡,𝜃



→𝑧



𝑡

𝜃



𝑚𝑖𝑛



𝐿[𝑦



,𝑧





𝜃



where 𝑀 specifies the model class, which contains a

given number of settable parameters 𝜃, and 𝐿 a loss

function which is minimized by estimating the

parameters 𝜃 to increase the fitting of the model’s

response 𝑧 for a given input 𝑥 on an empirical set of

𝑁 real world observations 𝑦



to a specific movement

in time 𝑡. This definition unifies all models on a base

level from which further subdivision can take place.

2.1.1 White-Box Modeling

Following Ljung's general approach to modeling,

white-box models can be defined by the same two

steps: modeling and fitting. The defining

characteristic of white-box models lies primarily in

the modeling phase, where the model class 𝑀 is

specified based on prior theoretical knowledge, such

as first-principle equations or domain-specific

insights. This phase determines the structure of the

model, with parameters 𝜃 often representing directly

interpretable physical properties or system dynamics.

The fitting process, though necessary, is typically

straightforward and involves optimizing 𝜃 to

minimize a loss function 𝐿 , aligning the model's

response 𝑧



𝑡

𝜃



with empirical observations 𝑦



. The

loss function ensures the model's output remains

consistent with observed data but does not

significantly influence the inherent transparency of

the model itself. This unique property is the origin of

the general reputation of transparency and

interpretability of white-box models. However, due to

their focus in modeling white-box models have a

tendency to require substantial computational effort

(Ralph et al. 2021). A well-known example for white-

box models are differential equation models.

2.1.2 Black-Box Modeling

Following Ljung's general approach to modeling,

black-box models are also defined by the two steps of

modeling and fitting. However, the defining

characteristic of black-box models lies predominantly

in the fitting phase, where the parameters 𝜃 are

calibrated extensively using observed data to achieve

an optimal match between the model's response and

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

314

empirical measurements. In black-box models, the

modeling phase is minimal and typically involves

selecting a general-purpose model class 𝑀 without

specific links to the underlying system's physical or

logical structure. Common choices include neural

networks (Dayhoff and DeLeo 2001), support vector

machines (Dinov 2018) and also traditionally

speaking linear regression models (Guidotti et al.

2018), which are flexible enough to approximate

complex input-output relationships. The fitting

process, in contrast, plays a central role, as it adjusts

the free parameters 𝜃 to minimize the loss function 𝐿.

This process ensures that the model's response 𝑧



𝑡

𝜃



aligns closely with the observed data 𝑦



, often at the

cost of interpretability and transparency. Moreover,

the interpretability and transparency of the model

further decrease as the number of free parameters 𝜃

increases.

2.1.3 Grey-Box Modeling

As mentioned in the introduction, grey-box models

represent a hybrid approach that incorporates both

qualities of white-box and black-box models.

Following Ljung's general modeling approach, grey-

box models would involve specifying a model class

𝑀 that incorporates both known physical principles

and parameters 𝜃 calibrated to align with real-world

data. Looking into different grey-box modeling

implementations, the overall main goal of this hybrid

form is the offset one or multiple disadvantages of the

individual approaches, whether it is the lack of

transparency in black-box models (Loyola-González

2019) or the growing computational complexity of

white-box models (Li et al. 2021). Depending on the

task at hand grey-box approaches can be rolled out as

a serialization or parallelization of one or multiple

white- and black-box models (Yang et al. 2017),

(Sohlberg and Jacobsen 2008). However, the dual

nature of grey-box models comes at a cost. The

integration of theoretical knowledge and empirical

data requires additional effort in both model design

(modeling) and parameter optimization (fitting).

2.2 Modern Requirements on Modeling

2.2.1 Transparency

Transparency in modeling refers to the extent to

which model creation, parameter extraction, and

output generation can be understood and explained. It

includes three sub-aspects: model transparency,

design transparency and algorithmic transparency

(Roscher et al. 2020). While some methods, like

kernel-based models (Hofmann, Schölkopf, and

Smola 2008), are often transparent in structure,

design choices may lack clarity. Neural networks,

despite clear input-output structures, involve heuristic

design and hyper-parameter tuning, reducing

transparency.

2.2.2 Interpretability

In the context of black- and white-box models

interpretability refers to the ability to present the

internal properties or decisions of a model in

understandable terms to humans (Roscher et al.

2020). It involves mapping abstract model concepts,

such as predictions, into forms comprehensible to

users. For black-box models, interpretability often

relies on post hoc methods, such as proxy models

(Ribeiro, Singh, and Guestrin 2016), feature

importance analysis (König et al. 2021), or visual

tools like saliency maps (Hohman et al. 2019). White-

box models, due to their inherent transparency,

facilitate interpretation by design. Achieving

interpretability often requires data involvement and

may depend on heuristic approaches when

algorithmic explanations are complex or infeasible.

2.2.3 Explainability

In modeling, explainability refers to the ability to

provide clear and understandable reasons or

justifications for a model's predictions or decisions. It

builds on interpretability by contextualizing model

behavior with domain knowledge. While

interpretability focuses on understanding model

components, explainability emphasizes clarifying the

reasoning behind decisions, often combining

interpretation tools, transparency, and domain-

specific insights to provide meaningful explanations

(Roscher et al. 2020).

2.2.4 Domain Knowledge

Incorporating domain or theoretical knowledge into

modeling enhances explainability, improves

performance, and helps address small data scenarios.

It encompasses expertise or information specific to a

field, ranging from mathematical equations and rules

in the sciences to engineering workflows, world

knowledge, or expert intuition. Integration involves

three key aspects: the type of knowledge, its

representation and transformation, and its application

in the ML pipeline (Rueden et al. 2021). This can

occur during data preparation, hypothesis design,

training, or evaluation. Leveraging domain

knowledge aligns models with real-world

An Engineer-Friendly Terminology of White, Black and Grey-Box Models

315

applications, making them more interpretable and

effective.

2.2.5 Computational Effort

Computational effort or computational complexity

impacts both white-box and black-box models

differently. The live-cycle of a model can be roughly

separated into two phases: the development phase,

where a model is developed, and the application

phase, where a finalized model is in usage. Black-box

models generally require significant resources in the

development phase during data fitting and

optimization, whereas white-box models have a

tendency to rather require more in the application

phase (Boos et al. 2023). Nonetheless, although the

processing power of computers grow continuously,

computational effort and complexity remain critical

considerations (Shahcheraghian, Madani, and Ilinca

2024).

2.2.6 Realism

The level of realism refers to how accurately the

model is able to reflect the underlying system. White-

box models, while grounded in physical laws and

theoretical principles, often rely on simplifications,

which limit their level of realism. However, as the

complexity of a white-box model increases and the

number of model parameters grows, its ability to

capture real-world behaviors improves. This

improvement, nevertheless, comes with the drawback

of a higher computational complexity (Fujimoto et al.

2017). In contrast, black-box models achieve realism

by leveraging empirical data, allowing them to model

complex systems effectively. However, this data-

driven approach may introduce overfitting or fail to

incorporate underlying causal relationships, reducing

interpretability.

2.3 Deficits

Both white-box and black-box models have inherent

deficits that limit their application in certain

scenarios, leading to a growing preference for

hybrid grey-box approaches. Generally speaking,

the tendency towards grey-box models stems from

the goal to eliminate at least one modeling weakness

by incorporating one or more of the presented

requirements on modeling (see Section 2.5). On that

regard a recommendation for action does not exist.

The current state-of-the-art does not include a

methodology to guide an engineer towards a

strategic extension of a given base model to actively

address weaknesses. Nonetheless, in the traditional

sense there are essentially two paths to model

improvement: moving from white-box to grey-box,

and moving from black-box to grey-box.

2.3.1 Transitioning from White to Grey

Transitioning from white-box to grey-box involves

integrating data-driven components. One of the most

elemental reasons to integrate more data into a white-

box model is to improve the accuracy of the model

(with calibration) (Mostafavi et al. 2018). Another

reason is the transition of the computational effort

from the application phase to the development phase

aiming to speed up the computational time during

active application. This can be used for small sections

of a white-box model (Stöcker et al. 2023) or even for

the full white-box model itself by creating a surrogate

model (Böttcher, Fuchs, et al. 2021), (Böttcher,

Leichsenring, et al. 2021). Besides the computational

effort, rising complexity can be another reason to

move from white- to grey-box models. In some cases

the necessary human effort to model physical

relations correctly surpasses the effort to collect

empirical data by a multitude due to complexity. In

these cases including black-box approaches into your

white-box model to approximate complex non-linear

relations can be helpful (Shahcheraghian et al. 2024).

2.3.2 Transitioning from Black to Grey

Transitioning from black-box to grey-box involves

integrating interpretability, explainability and

transparency by embedding reasoning into the

model structure. One widely known approach

aiming for improved transparency is explainable

artificial intelligence (XAI) (Minh et al. 2022; Rane

and Paramesha 2024). It provides insights into the

model’s decision process, bridging the gap between

the model's opaque internal workings and user

interpretability. Another approach to enhance

interpretability is by incorporating domain

knowledge, which is aimed for in Physics-Informed

Machine Learning (PIML) (Xu et al. 2023). PIML

integrates physical laws, constraints, and governing

equations directly into the black-box model. By

embedding physical laws and domain insights,

PIML can reduce the dependence on large data sets,

improve model generalization, and minimize false

discoveries, making it particularly suitable for

engineering applications where data may be sparse

or financially expensive to obtain (Mackay and

Nowell 2023).

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

316

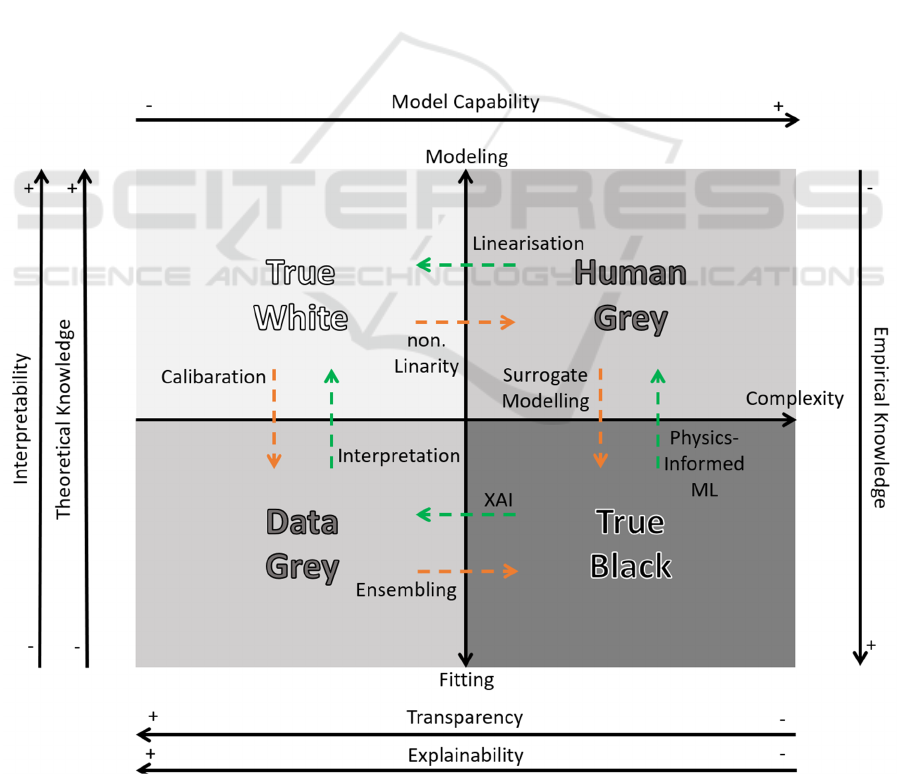
3 PROPOSED TERMINOLOGY

FOR MODELING

3.1 Dual-Axis Scale for Model

Classification

With the rising complexity of models in engineering

to correctly map reality, a clear tendency is emerging

towards hybrid modeling such as grey-box models.

The number of possibilities to numerically model

reality is also growing with further research, offering

multiple permutations to combine different modeling

approaches. The definition of white- and black-box

models shifted from their modeling approaches to

their application requirements. This paper proposes a

new engineering friendly terminology that unites the

modern point of view to modeling with the traditional

one. This terminology includes a subdivision of two

different types of grey-box models. The goal of this

proposed view is to further break down these three

basic terms by their relation towards each other.

Our proposed model and terminology aim to

depict white- and black-box models on a dual-axis

scale, as shown in Figure 1. The x-axis represents the

complexity of a model. This value is relative and can

be portrayed by a set of qualities such as complexity

through number of adjustable parameters, increasing

levels of abstraction or non-linearity, interconnected

variables and emergent behaviors that challenge

straightforward human comprehension. However,

with rising complexity, model capability generally

increases as well. More complex models tend to be

better equipped to capture intricate patterns, handle

high-dimensional data, and solve sophisticated

problems that simpler models might struggle with.

The y-axis represents the 2 phases of modeling (see

Section 2.1) on a continuous scale. The upper values

represent the modeling phase, while the lower values

the fitting phase. It reflects the interpretability, to

which extend the internal workings of the model and

its decision-making processes can be understood by

humans. If the proposed model is interpreted as a

geographical map, then the following accounts: The

Figure 1: Proposed dual-axis model.

An Engineer-Friendly Terminology of White, Black and Grey-Box Models

317

more north a model is located the more it is defined by

the modeling phase, while the more south it is, the

more it is defined by the fitting phase. Likewise, on the

complexity axis, the more west a model is located the

easier it is to be fully understood by a human, while the

further east it moves, the more intricate it becomes.

This mapping results in four quadrants. The first

quadrant represents a true white-box model: it is a

knowledge-based modeling approach, transparent,

explainable, interpretable thus easy to understand for a

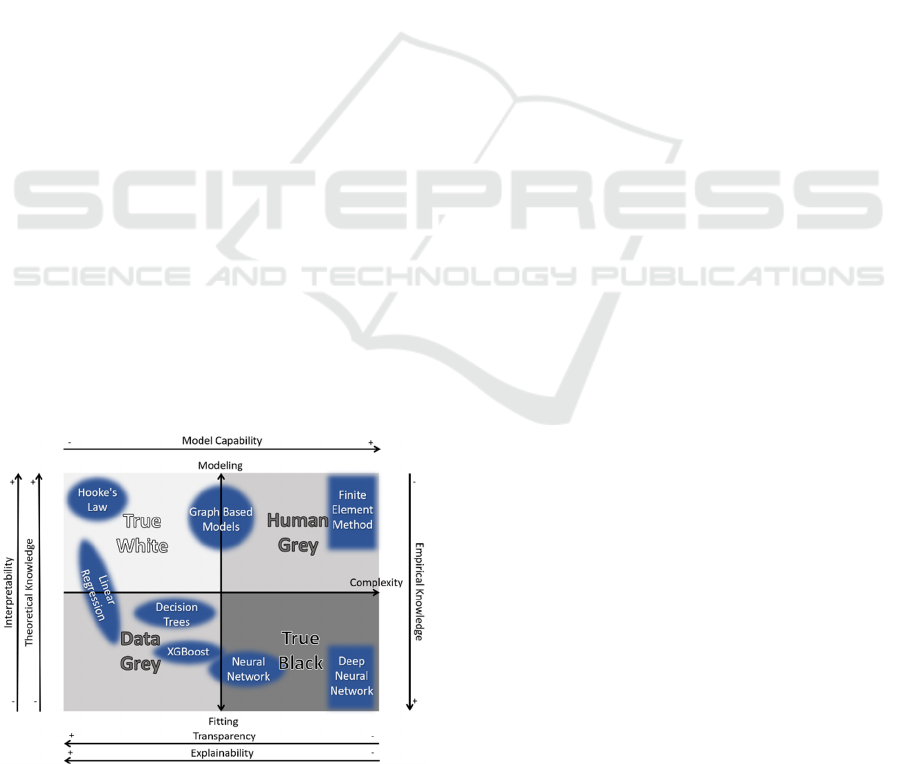
human. Hook’s law is an example for a true white-box

model (see Figure 2). On the contrary, in the fourth

quadrant, the true black-box model is positioned: it is a

modeling approach based on empirical data fitting,

highly complex and opaque but also highly powerful

in their ability to map non-linearity. An example for a

true black-box model is a deep neural network. The

second and third quadrant are both different types of

grey-box models. The second quadrant, which,

compared to the first quadrant, increases in

complexity, but remains consistent in interpretability.

We propose the name human-grey for this quadrant.

By increasing the complexity and thus model

capability, this kind of grey-box model, loses

transparency and explainability. However, in its core,

it remains a model, which is developed by the

modeling phase. The finite element method is

exemplary for a human-grey model. In contrast, the

third quadrant, depicts a model, which, identical to a

true black-box model, is based on the fitting phase of

model design but on par in transparency and

explainability with white-box models. We propose the

name data-grey. Although developed with mainly

empirical data, a data-grey model maintains sufficient

transparency to ensure that its decision-making process

is comprehensible to a human observer. Decision trees

are one example for a data-grey model.

Figure 2: Positioning of different vanilla model classes

within the dual-axis scale.

This dual-axis scale allows for a comprehensive

visualization of models, highlighting trade-offs

between their complexity and interpretability, and

enabling a more nuanced discussion about their

suitability for different applications. Figure 2

illustrates the placement on the dual-axis scale of

several common model classes as examples.

3.2 Benefits

The proposed model and terminology include three

main benefits compared to the conventional point of

view. The main benefit encompasses a more precise

classification and distinction between existing vanilla

modeling classes (see Figure 2). Furthermore, it

enables a fuzzy classification for model classes,

which can be placed in more than one quadrant due to

their inherent properties and capabilities. For

instance, a linear regression model, while classified

as a white-box model due to its inherent

interpretability, may transition toward black-box

behavior as the volume of data increases. In such

cases, the rising complexity can obscure the model's

transparency. Labeling it as a black-box model,

however, can be misleading when compared to a deep

neural network. The classification data-grey model –

a model which is based on data driven methods but

still transparent and explainable -is more suitable.

Similarly, a simple fully connected neural network,

although technically labeled as a black-box model, is

transparent and explainable in its architecture and

operation. While on the other hand more complex

neural networks, such as convolutional neural

networks (CNN) or recurrent neural networks (RNN),

are less transparent, making their decision-making

processes significantly harder to interpret and

explain. All in all a further distinction between

different model classes and their property assessment

is suggested.

Another similar benefit is the more precise

distinction of state-of-the-art approaches, which aim

to eliminate a limitation compared to its base vanilla

model class. One prevalent example is XAI. It

describes a set of methods or model architectural

features to further enhance transparency and

explainability of data-driven models. XAI is aiming

to transition from a true black-box model to become

data-grey, thus transitioning from the fourth quadrant

to the third. Another state-of-the-art example is

PIML. By including physical laws into the machine

learning algorithm, interpretability is further

enhanced, moving the model class from back-box to

human-grey. However, as domain knowledge is

included and therefore interpretability improved, the

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

318

movement occurs along a different feature. XAI as

well as PIML are both implementing white-box

model characteristics, but respectively different ones.

The proposed dual-axis scale illustrates this

distinction. Figure 1 shows examples for each change

of quadrants.

Following the benefit of an improved

classification for the “hybridization” of models, a

reverse effect follows suit. The proposed dual-axis

scale allows the derivation of recommendations for

action. An engineer, who due to given conditions is

limited to the usage of a specific vanilla model class,

is able to derive necessary actions to improve certain

criteria of the given vanilla model class. For instance,

the development of physical models is out of budget,

but a small sample of experimental data was

collected. The development of a decision tree model

is applicable, but does not result in sufficiently good

results. This situation can be classified as data-grey.

A possible step up, increasing model capability for

the cost of transparency and explainability would be

the usage of ensembling techniques. XGBoost offers

a preset ensembling solution but also custom

ensembling strategies are feasible.

4 CONCLUSIONS

White-box and black-box models represent

foundational approaches in the modeling of

engineering systems, each with distinct strengths and

limitations. Combining these two modeling

approaches to add up strengths and offset limitations,

has been the prevalent tendency in recent years.

Hereby, the same term “grey-box” model has been

used to describe different hybrid modeling strategies.

This paper proposes a new point of view to the creation

and labelling of grey-box models based on the inherent

modern requirements on models in engineering spaces.

It introduces two new terms: data-grey and human-

grey model. Both terms describe different

characteristics of grey-box models. Distinguishing

between them allows the user to better classify the

properties and qualities of a model class. Data-grey

models emphasize the incorporation of empirical data

to refine and calibrate model parameters while

maintaining a foundational transparent and explainable

structure. In contrast, human-grey models prioritize the

interpretability of the model, enabling users to

understand and trust the decision-making process but

leveraging model capability by increasing complexity.

Together, these concepts expand the traditional

definition of grey-box models, addressing modern

engineering requirements.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge funding by the

German Research Foundation (DFG) - funding

number IH 123/32-1 as well as the Federal Ministry

of Education and Research (BMBF) – funding

number 033KI129.

REFERENCES

Bohlin, Torsten, ed. 2006. Practical Grey-Box Process

Identification: Theory and Applications. Springer

London.

Boos, E., X. Thiem, H. Wiemer, and S. Ihlenfeldt. 2023.

“Improving a Deep Learning Temperature-Forecasting

Model of a 3-Axis Precision Machine with Domain

Randomized Thermal Simulation Data.” Pp. 574–84 in

Production at the Leading Edge of Technology,

Lecture Notes in Production Engineering, Springer

International Publishing.

Böttcher, Maria, Alexander Fuchs, Ferenc Leichsenring,

Wolfgang Graf, and Michael Kaliske. 2021. “ELSA:

An Efficient, Adaptive Ensemble Learning-Based

Sampling Approach.” Advances in Engineering

Software 154:102974.

Böttcher, Maria, Ferenc Leichsenring, Alexander Fuchs,

Wolfgang Graf, and Michael Kaliske. 2021. “Efficient

Utilization of Surrogate Models for Uncertainty

Quantification.” PAMM 20(1):e202000210.

Dayhoff, Judith E., and James M. DeLeo. 2001. “Artificial

Neural Networks.” Cancer 91(S8):1615–35.

Dinov, Ivo D. 2018. “Black Box Machine-Learning

Methods: Neural Networks and Support Vector

Machines.” Pp. 383–422 in Data Science and

Predictive Analytics: Biomedical and Health

Applications using R, Springer International

Publishing.

Fujimoto, Richard, Conrad Bock, Wei Chen, Ernest Page,

and Jitesh H. Panchal, eds. 2017. Research Challenges

in Modeling and Simulation for Engineering Complex

Systems. Cham: Springer International Publishing.

Guidotti, Riccardo, Anna Monreale, Salvatore Ruggieri,

Franco Turini, Fosca Giannotti, and Dino Pedreschi.

2018. “A Survey of Methods for Explaining Black Box

Models.” ACM Comput. Surv. 51(5):93:1-93:42.

Hofmann, Thomas, Bernhard Schölkopf, and Alexander J.

Smola. 2008. “Kernel Methods in Machine Learning.”

The Annals of Statistics 36(3):1171–1220.

Hohman, Fred, Minsuk Kahng, Robert Pienta, and Duen

Horng Chau. 2019. “Visual Analytics in Deep

Learning: An Interrogative Survey for the Next

Frontiers.” IEEE Transactions on Visualization and

Computer Graphics 25(8):2674–93.

König, Gunnar, Christoph Molnar, Bernd Bischl, and

Moritz Grosse-Wentrup. 2021. “Relative Feature

Importance.” Pp. 9318–25 in 2020 25th International

Conference on Pattern Recognition (ICPR).

An Engineer-Friendly Terminology of White, Black and Grey-Box Models

319

Li, Yanfei, Zheng O’Neill, Liang Zhang, Jianli Chen, Piljae

Im, and Jason DeGraw. 2021. “Grey-Box Modeling and

Application for Building Energy Simulations - A

Critical Review.” Renewable and Sustainable Energy

Reviews 146:111174.

Ljung, Lennart. 1996. System Identification: Theory for the

User. 9. [print.]. Upper Saddle River, NJ: Prentice-Hall

PTR.

Loyola-González, Octavio. 2019. “Black-Box vs. White-

Box: Understanding Their Advantages and Weaknesses

From a Practical Point of View.” IEEE Access

7:154096–113.

Mackay, Calum Torin, and David Nowell. 2023. “Informed

Machine Learning Methods for Application in

Engineering: A Review.” Proceedings of the Institution

of Mechanical Engineers, Part C: Journal of

Mechanical Engineering Science 237(24):5801–18.

Minh, Dang, H. Xiang Wang, Y. Fen Li, and Tan N.

Nguyen. 2022. “Explainable Artificial Intelligence: A

Comprehensive Review.” Artificial Intelligence Review

55(5):3503–68.

Mittal, Saurabh, and Andreas Tolk. 2019. Complexity

Challenges in Cyber Physical Systems: Using Modeling

and Simulation (M&S) to Support Intelligence,

Adaptation and Autonomy.

Mostafavi, Saman, Robert Cox, Benjamin Futrell, and

Roshanak Ashafari. 2018. “Calibration of White-Box

Whole-Building Energy Models Using a Systems-

Identification Approach.” Pp. 795–800 in IECON 2018

- 44th Annual Conference of the IEEE Industrial

Electronics Society.

Pintelas, Emmanuel, Ioannis E. Livieris, and Panagiotis

Pintelas. 2020. “A Grey-Box Ensemble Model

Exploiting Black-Box Accuracy and White-Box

Intrinsic Interpretability.” Algorithms 13(1):17.

Ralph, Benjamin James, Karin Hartl, Marcel Sorger,

Andreas Schwarz-Gsaxner, and Martin Stockinger.

2021. “Machine Learning Driven Prediction of

Residual Stresses for the Shot Peening Process Using a

Finite Element Based Grey-Box Model Approach.”

Journal of Manufacturing and Materials Processing

5(2):39.

Rane, Nitin Liladhar, and Mallikarjuna Paramesha. 2024.

“Explainable Artificial Intelligence (XAI) as a

Foundation for Trustworthy Artificial Intelligence.” in

Trustworthy Artificial Intelligence in Industry and

Society. Deep Science Publishing.

Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin.

2016. “‘Why Should I Trust You?’: Explaining the

Predictions of Any Classifier.” Pp. 1135–44 in

Proceedings of the 22nd ACM SIGKDD International

Conference on Knowledge Discovery and Data Mining,

KDD ’16. New York, NY, USA: Association for

Computing Machinery.

Roscher, Ribana, Bastian Bohn, Marco F. Duarte, and

Jochen Garcke. 2020. “Explainable Machine Learning

for Scientific Insights and Discoveries.” IEEE Access

8:42200–216.

Rudin, Cynthia. 2019. “Stop Explaining Black Box

Machine Learning Models for High Stakes Decisions

and Use Interpretable Models Instead.” Nature

Machine Intelligence 1(5):206–15.

Rueden, Laura von, Sebastian Mayer, Katharina Beckh,

Bogdan Georgiev, Sven Giesselbach, Raoul Heese,

Birgit Kirsch, Julius Pfrommer, Annika Pick, Rajkumar

Ramamurthy, Michal Walczak, Jochen Garcke,

Christian Bauckhage, and Jannis Schuecker. 2021.

“Informed Machine Learning -- A Taxonomy and

Survey of Integrating Knowledge into Learning

Systems.”

Shahcheraghian, Amir, Hatef Madani, and Adrian Ilinca.

2024. “From White to Black-Box Models: A Review of

Simulation Tools for Building Energy Management and

Their Application in Consulting Practices.” Energies

17(2):376.

Shakerin, Farhad, and Gopal Gupta. 2020. “White-Box

Induction From SVM Models: Explainable AI with

Logic Programming.” Theory and Practice of Logic

Programming 20(5):656–70.

Sohlberg, B., and E. W. Jacobsen. 2008. “GREY BOX

MODELLING – BRANCHES AND EXPERIENCES.”

IFAC Proceedings Volumes 41(2):11415–20.

Stöcker, Julien Philipp, Elsayed Saber Elsayed, Fadi

Aldakheel, and Michael Kaliske. 2023. “FE-NN:

Efficient-Scale Transition for Heterogeneous

Microstructures Using Neural Networks.” PAMM

23(3):e202300011.

Wiemer, Hajo, Dorothea Schneider, Valentin Lang, Felix

Conrad, Mauritz Mälzer, Eugen Boos, Kim Feldhoff,

Lucas Drowatzky, and Steffen Ihlenfeldt. 2023. “Need

for UAI–Anatomy of the Paradigm of Usable Artificial

Intelligence for Domain-Specific AI Applicability.”

Multimodal Technologies and Interaction 7(3):27.

Xu, Yanwen, Sara Kohtz, Jessica Boakye, Paolo Gardoni,

and Pingfeng Wang. 2023. “Physics-Informed Machine

Learning for Reliability and Systems Safety

Applications: State of the Art and Challenges.”

Reliability Engineering & System Safety 230:108900.

Yang, Zhuo, Douglas Eddy, Sundar Krishnamurty, Ian

Grosse, Peter Denno, Yan Lu, and Paul Witherell. 2017.

“Investigating Grey-Box Modeling for Predictive

Analytics in Smart Manufacturing.” P. V02BT03A024

in Volume 2B: 43rd Design Automation Conference.

American Society of Mechanical Engineers.

MODELSWARD 2025 - 13th International Conference on Model-Based Software and Systems Engineering

320