Pre-Training Deep Q-Networks Eliminates the Need for Target
Networks: An Empirical Study
Alexander Lindstr
¨
om
a
, Arunselvan Ramaswamy
∗ b
and Karl-Johan Grinnemo
c
Department of Mathematics and Computer Science, Karlstad University, Universitetsgatan 2, 65188 Karlstad, Sweden
Keywords:
Deep Q-Network, Deep Q-Learning, Stability, Pre-Training, Variance Reduction.
Abstract:
Deep Q-Learning is an important algorithm in the field of Reinforcement Learning for automated sequential
decision making problems. It trains a neural network called the Deep Q Network (DQN) to find an optimal
policy. Training is highly unstable with high variance. A target network is used to mitigate these problems, but
leads to longer training times and, high training data and very large memory requirements. In this paper, we
present a two phase pre-trained online training procedure that eliminates the need for a target network. In the
first - offline - phase, the DQN is trained using expert actions. Unlike previous literature that tries to maximize
the probability of picking the expert actions, we train to minimize the usual squared Bellman loss. Then,
in the second - online - phase, it continues to train while interacting with an environment (simulator). We
show, empirically, that the target network is eliminated; training variance is reduced; training is more stable;
when the duration of pre-training is carefully chosen the rate of convergence (to an optimal policy) during the
online training phase is faster; the quality of the final policy found is at least as good as the ones found using
traditional methods.
1 INTRODUCTION
Reinforcement Learning (RL) is a paradigm in AI
used to solve complex sequential decision making
problems, which can be formalized using Markov
Decision Processes (MDP). Traditional approaches
of RL required full knowledge of the sequential
decision-making problem at hand, making it inappro-
priate for large complex problems with a large num-
ber of complex scenarios (Mnih et al., 2015). To
overcome these limitations, a Neural Network (NN) is
combined with traditional RL ideas to develop Deep
Q Learning (DQL), which has since then become
the most popular modern RL algorithm (Mnih et al.,
2015). In DQL, a neural network called DQN is
trained to minimize the squared Bellman loss func-
tion. Minimizing this loss allows DQN to find the
optimal policy, i.e., the sequence of decisions to solve
the original problem at hand.
DQL signifies a significant advancement in AI.
However, integrating NNs with RL presents numer-
a
https://orcid.org/0000-0003-0222-7658
b
https://orcid.org/0000-0001-7547-8111
c
https://orcid.org/0000-0003-4147-9487
∗
Ramaswamy was partially supported by The Knowl-
edge Foundation (grant no. 20200164).
ous challenges, e.g., typically NNs require large
amounts of data for training, numerical instability
during NN training is a particular issue in RL as the
nature of the decision making problem is complex, to
begin with. To address such issues, DQL introduced
two key mechanisms: “the replay buffer” and “the
target network”. The replay buffer facilitates contin-
uous learning from past and current experiences in
the same measure. Meanwhile, the target network,
as claimed by the authors, reduces instability during
learning. Essentially, the target network is just a copy
of the main network, but in comparison, it gets up-
dated less frequently by taking a new copy of the
main network (Ramaswamy et al., 2023), (Mnih et al.,
2013).
While these mechanisms are pertinent for success-
ful learning, they result in large overheads and high
memory demands, which ultimately slow down learn-
ing (Yang et al., 2021). Despite its success, using
a target network DQL lacks significant investigation
of its importance during different scenarios. For this
study, we aim to investigate whether the reliance on
the target network can be reduced or even eliminated
under certain conditions, thereby reducing memory
usage of DQL and maintenance overheads without
compromising its performance.
Lindström, A., Ramaswamy, A. and Grinnemo, K.-J.
Pre-Training Deep Q-Networks Eliminates the Need for Target Networks: An Empirical Study.
DOI: 10.5220/0013374600003905
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 14th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2025), pages 437-444
ISBN: 978-989-758-730-6; ISSN: 2184-4313
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
437

A DQN is trained using data generated through re-
peated interactions with the environment in which the
decision making problem is being solved. Each in-
teraction warrants a feedback which then improves its
performance. As the DQN weights are randomly ini-
tialized the interaction is suboptimal or even danger-
ous at the beginning. In order to overcome this issue,
a DQN is pre-trained using data associated with ex-
pert interactions with the environment. As this stage
is before the DQN gets to interact with the environ-
ment, the previously mentioned dangers are averted.
The pre-training phase is also called the offline learn-
ing phase. The training phase where the DQN in-
teracts with the environment (and continues to train)
is called the online phase. Training DQNs in two
phases, offline followed by an online phase, is a pop-
ular and practical training paradigm. This will the fo-
cus of this paper.
1.1 Problem Description and Our
Contribution
While a target network has been demonstrated to be
useful in stabilizing learning for DQL, its contribution
to finding better policies remains under-explored. In
(Mnih et al., 2015), the significance of a target net-
work is highlighted in mitigating the moving target
problem and in enhancing stability. However, there is
a lack of empirical evidence for its necessity through-
out the entire training process (Mnih et al., 2015). Re-
cent mathematical proofs, e.g., in (Ramaswamy and
H
¨
ullermeier, 2022) suggest that the target network
could be removed at certain stages of training. These
proofs consider both the online and offline phases
of learning. Recall that online learning refers to the
learning paradigm wherein the learning agent influ-
ences the data used for training in a direct “ongoing”
manner. In offline learning, the agent is trained us-
ing data that was collected in the past - pre-training
- and often the agent has no influence on this train-
ing data (Hester et al., 2017). As mentioned before
an offline learning phase (pre-training) typically pre-
cedes an online learning phase. This kind of training
is called pre-trained online learning.
1. When an agent is trained in two phases - the of-
fline followed by an online phase, a target network
can be completely omitted.
2. In order to find the best policy, we observed that
there is an optimal amount of pre-training. Too
little affects stability during the online phase, too
much affects optimality.
3. As compared to training with a target network, the
training without a target network has lower vari-
ance. Hence, learning is faster!
1.2 Related Work
There have been several other works that have ques-
tioned the superfluity of a target network. For ex-
ample, in (Ramaswamy et al., 2023), it is suggested
that the target network could be removed in online
learning by replacing the activation function used in
the DQN with their newly developed Truncated Gaus-
sian Error Linear Unit (TGeLU) activation function
(Ramaswamy et al., 2023). This paper seeks to ad-
dress the practical implications of these theoretical
insights. The central question guiding this research is:
“How does the removal of the target network at vari-
ous scenarios and stages of training impact the stabil-
ity and effectiveness of DQL?”
In DQL, a target network is employed alongside
the main network during the training process to calcu-
late the Mean Square Error (MSE) loss. The primary
purpose of integrating a target network in DQL train-
ing is to address the moving target problem, which
arises from high variance in Q-value estimates, lead-
ing to unstable learning. In addition to the moving tar-
get problem affecting stable learning, NNs using non-
linear activation functions also suffer from a problem
referred to as numerical instability or exploding gra-
dient, which is caused by high variance. During the
backpropagation phase, the gradient will grow expo-
nentially, and if the loss value gets too high, this will
result in the weights becoming too large to handle
(Philipp et al., 2018).
By using a target network with less frequent up-
dates. This means that the target Q-values change
more slowly and are suggested to contribute to a
smoother training process, allowing for more reliable
convergence to an optimal policy, but at the same
time may slow down the learning process (Mnih et al.,
2015). Using a target network will also contribute to
a higher memory-consuming due to the need to keep
a copy of the network during training, which makes
the memory demand twice as much compared to only
using the main network. While it may be useful at
the beginning of the training to use a target network
to obtain stable learning, there is no proof that using
one will result in better policies.
Removing the target network to reduce the overes-
timation of Q-values and decrease memory demand is
not a novel idea per se, but the approach to removing
the target network and some of the findings we have
discovered are new. In this paper, we have been able
to show that it is possible for an agent to achieve just
as good or better policy than an agent trained with a
target network for the entire process without any ma-
ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods
438

jor modifications to the original algorithm. The fol-
lowing three papers present suggested modified DQL
algorithms, all of which focus on online learning and
aim to remove or reduce the usage of a target network
in order to stabilize the learning better. These are then
followed by two cases suggesting different methods
used to optimize training with a combination of of-
fline and online learning.
The paper (Van Hasselt et al., 2016) aims to con-
tribute to stable learning by lowering the overestima-
tion of Q-values. When Q-values are overestimated,
the agent believes certain actions’ values to be higher
than they actually are. This can lead to the agent mak-
ing suboptimal decisions, resulting in higher variance
in the Q-value estimates. While Double Q-learning
(DDQL) still uses a target network, its use is loosened
in contrast to DQL. In DQL, the target network pro-
vides the numerical value for the future calculation of
the current Q-value. However, in DDQL, the target
network is only used to estimate future actions, while
all numerical value contributions are provided by the
main network.
In the paper (Kim et al., 2019), the authors argue
that removing the target network in the case of online
learning achieves both faster and more stable learn-
ing. The approach here is to replace the max oper-
ator used in the Bellman equation with Mellowmax
because the max operator suffers from overestima-
tion. However, Mellowmax also suffers from overes-
timation, but to address this problem is the parameter
(ω) introduced to decrease the overestimations. Al-
though DeepMellow demonstrated higher cumulative
rewards for most compared cases compared to DQL,
parameter tuning still has some limitations to choos-
ing the most optimal ω. For larger problems, this tun-
ing process may be very exhaustive (Kim et al., 2019).
In the paper (Yang et al., 2021), the aim here as
well is to remove the target network by replacing the
loss function MSE and instead use Random Hybrid
Optimization (RHO). RHO is based on Hybrid Op-
timization (HO), which is a technique used to get a
tradeoff for the gradients between different optimiza-
tion methods, Mean Squared Value Error (MSVE)
and Mean Square Bellman Error (MSBE). The dif-
ference with RHO compared to HO is that instead
of using both optimization methods simultaneously
and calculating a gradient for some value in between
the methods, RHO uses one optimization method at
a time for every update, but the method is randomly
selected (Yang et al., 2021)
In this paper, we also aim to demonstrate that the
target network could be removed if an agent is first
trained offline before continuing to train online. How-
ever, mitigating the target network in offline learning
is not a well-explored area. In the case of related
work, the closet resembling our works comes from
the paper (Cruz Jr et al., 2019), which focus on com-
paring different configurations and setups applied for
pre-training in combination with DQL (Cruz Jr et al.,
2019), and the paper (Hester et al., 2017) present
a new algorithm combining pre-training and online
learning (Hester et al., 2017). But while these pa-
pers do not suggest or focus on reducing or removing
the target network, these methods are similar to ours,
except that we will not use a target network when we
combine offline and online learning.
2 NEURAL NETWORK
ARCHITECTURE AND MODEL
TRAINING
This empirical study aims to evaluate and determine
whether the highly memory-demanding target net-
work can be removed without compromising learning
stability. The reason to remove the target network is
not only because it’s highly memory-demanding but
also to contradict the statement that using a target
network would result in a policy closer to optimality.
The study investigates pre-trained online learning (of-
fline phase followed by an online phase). Although,
we believe that our conclusions can be replicated in
other RL algorithms as well. We begin by introduc-
ing the training and evaluation environments for the
agents. Subsequently, we present the architecture of
the DQN and provide a step-by-step explanation of
how the training process is carried out, both online
and offline.
2.1 Environment
Figure 1: Screenshot of the “CartPole-v1” environment.
We use the “CartPole-v1” environment from OpenAI
Pre-Training Deep Q-Networks Eliminates the Need for Target Networks: An Empirical Study
439

Gym. OpenAI Gym is a Python API standard that
provides a collection of environments for training and
testing RL algorithms. The “CartPole-v1” environ-
ment simulates an inverted pendulum, as illustrated
in Figure 1. The primary objective in this environ-
ment is to prevent a pole pivoted at a point on the cart
from falling by pushing the cart to the left or right on
a track. The ’CartPole-v1’ environment comes with
an action space, observation space, range limitations
for the observation space, and a reward function. In
our case, we use the standard configuration applied to
the current environment version, except for the reward
function.
2.1.1 Interaction with the Environment
Interacting with the environment begins with apply-
ing an action as a parameter, which returns parame-
ters: observation, reward, termination flag, truncation
flag, and additional information. In our case, we only
use the observation, termination, and truncation pa-
rameters. Additional information is primarily used
for debugging purposes, and for reward calculation,
we use our own constructed reward function.
2.1.2 Action and Observation Space
For the “CartPole-v1” environment, the action space
is discrete with two available actions:
• 0: Push the cart to the left on the track
• 1: Push the cart to the right on the track
The observation space consists of four observa-
tions: cart position (x), cart velocity, pole angle (φ),
and pole angular velocity. Table 1 presents the details
of the observation space. If the cart is centered in the
middle of the screen and the pole stands straight up,
the position and angle are x = 0 and φ = 0, respec-
tively.
Table 1: Observation space for the “CartPole-v1” environ-
ment.
Observation Min Max
Cart position (x) -4.8 4.8
Cart velocity −∞ ∞
Pole angle (φ) -0.418 rad
1
0.418 rad
Pole angular velocity −∞ ∞
2.1.3 Termination Conditions and Reward
Function
Some limitations may trigger termination or trunca-
tion conditions to determine whether the environment
1
The angle is described in radians
was solved. If the termination flag is triggered, the
environment is “not solved”; if the truncated flag is
triggered, the environment is “solved”.
Termination Condition: the termination parameter
is triggered if either or both x /∈ [−2.4,2.4] and
φ /∈ [−0.2095, 0.2095] is true.
Truncation Condition: The truncation flag is trig-
gered if 500 steps have been taken, which is the
maximum number of steps for this environment.
For this study, we utilize the following reward
function:
reward =





10 if truncated
−10 if terminated
(1 − φ) + (5 − x) else
(1)
During the online training phase, where we inter-
act directly with the environment, each episode con-
sists of 500 steps. A reward is received for each step
of the training episode. If the environment is trun-
cated, meaning the maximum number of steps possi-
ble is reached, the agent is rewarded with +10. If the
environment terminates before 500 steps, the agent is
rewarded with −10. For all other steps, the agent re-
ceives a higher reward the closer the cart is to the mid-
dle and the closer the pole angle is to zero. The reward
function’s design encourages the agent to trigger the
truncated flag and keep the pole steady and balanced.
2.2 Agent Setup and Training Process
We want to use the environment to train agents for
both online and offline learning modes. Online learn-
ing is the most common training process for RL. In
online learning, we start with an empty replay buffer.
Throughout training and interaction with the environ-
ment, we populate the replay buffer with new expe-
riences obtained from the interaction and update the
weights of the DQN with mini-batches sampled from
the replay buffer. For offline learning, we begin with
a pre-filled replay buffer. The weights of the DQN
are updated using mini-batches sampled from the pre-
filled replay buffer without interacting with the envi-
ronment. While offline learning is not as common as
online learning, there are cases where it’s beneficial to
pre-train an agent before continuing the training on-
line. Therefore, we aim to evaluate the concept of
removing the target network for both scenarios: when
an agent trains only online and when it first pre-trains
before continuing to train online.
2.3 DQN Architecture
Our DQN consists of four layers: one input layer, two
hidden layers, and one output layer. The input and
ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods
440

output layers are adjusted to match the environment’s
observation and action spaces, respectively. In the
case of the “CartPole-v1” environment, the observa-
tion space is a 4-tuple, and the action space contains
two possible actions. Therefore, the input layer has
four neurons, and the output layer has two neurons. In
this case, we use two hidden layers containing 64 and
128 neurons using Sigmoid activations unless other-
wise specified.
2.4 Learning Rate and Exploration
Probability Decay
Next, we discuss the decay process during online
learning, where we use polynomial decay for both
the learning rate and exploration probability. During
training, when the learning loss is below 0.5 for 100
consecutive episodes, the learning rate is decayed us-
ing:
α = (α
initial
− α
min
) · (1 −
n
N
max
)
α
p
+ α
min
(2)
• n = current episode
• N
max
= maximum number of episode (In this case
set to 10000)
• α
initial
= initial rate (set to 0.02)
• α
min
= target rate (set to 0.0001)
• α
p
polynomial factor ( higher values results in a
faster decay, set to 2 for this case)
Next, we explain the decay of the exploration rate
ε. The exploration rate decays every 100 episode re-
gardless of how the agent performs, using the follow-
ing equation:
ε = (ε
initial
− ε
min
) · (1 −
n
N
max
)
ε
p
+ ε
min
(3)
• ε
initial
= 1
• ε
min
= 0.01
• ε
p
= 7
2.5 Step-by-Step Description of
Pre-Trained Online Learning
The pre-training is done as an offline learning phase,
where an agent is trained without interaction with
an environment. Instead, we use a pre-filled replay
buffer B to train the agent. The replay buffer contains
experiences collected from previous interactions with
the environment or from expert demonstrations.
Initialization
• Create a New DQN: Randomly initialize the NN
weights using a uniform distribution.
Training
1. Train for some number of iterations:
2. Sample Mini-Batch: Sample a mini-batch b with
experiences from the replay buffer B, denoted as
b ∼ U (B).
3. Update Network Weights: Update the network
weights by backpropagation using Stochastic Gra-
dient Descent (SGD) with the mini-batch b and
the loss function in Equation 4.
4. Repeat: Unless training is terminated, repeat
steps 2 and 3.
This process enables the agent to learn from previ-
ously collected experiences stored in the replay buffer
without interacting with the environment. This is now
followed by the online learning phase which now does
not use a target network, described below.
Initialization
1. Create a DQN: Initialize the NN to the pre-
trained DQN.
2. Initialize Replay Buffer: Create a replay buffer
B with a maximum capacity C to store experi-
ences.
Training
1. Train for some number of episodes:
2. Action Selection:
• With probability ε, select a
t
∼ U (A
t
).
• Otherwise, a
t
:= argmax
a
Q(s
t
,a;θ).
3. Store Experience: Store experience exp
t
=
(s,a,r,s
′
) in the replay buffer B
2
.
4. Sample Mini-Batch: Sample a mini-batch b with
experiences from the replay buffer B, denoted as
b ∼ U (B)
3
.
5. Update DQN Weights:
• Calculate the loss function L
i
(θ
i
) using the
mini-batch b.
L
i
(θ
i
) = E
(r,s,a,s
′
)∼U(B)

r(s, a, s
′
)+
γmax
a
′
Q(s
′
,a
′
;θ
i
) − Q(s,a; θ
i
)

2
(4)
2
Once the maximum capacity C is reached, experiences
are removed from the replay buffer in a First In First Out
(FIFO) order.
3
In the beginning, steps 4, 5, and 6 are skipped until the
amount of experience stored in the replay buffer is equal to
or greater than the mini-batch size specified for training
Pre-Training Deep Q-Networks Eliminates the Need for Target Networks: An Empirical Study
441

• Perform backpropagation using the SGD opti-
mizer.
6. Repeat: Unless training is terminated, repeat the
above steps.
3 EMPIRICAL RESULTS AND
ANALYSIS
During the offline phase, the agent is trained without
interacting with an environment. Instead, we use a
pre-filled experience replay buffer containing expert
experience and update the weights of the DQN for
n number of iterations using mini-batches uniformly
drawn from this buffer. After pre-training, we con-
tinue to train the agent, starting with the pre-trained
policy learnt during the offline phase. The old replay
buffer is discarded and we start the online learning
process with a empty one. We show through experi-
ments that a target network is redundant if the tradi-
tional online training is preceded by an offline phase
(pre-training). Our experiments show that: even with
discarding the target network completely, the agent
can find a policy that is as good, or better than, the
one found by an agent which trains using a target net-
work throughout the training process.
To show the superfluity of target networks when
pre-training is used, we compare the policy obtained
by a DQN trained with and without a target network
in offline learning. However, instead of training two
agents in parallel, we can train only one agent in pre-
trained online learning without a target network and
compare with the DQN trained with a target network
in online learning.
3.1 Impact of Pre-Training and
Learning Stability
Recall that a policy is deemed acceptable if it is
able to balance the cart-pole for all of the 500 steps
within an episode consistently for 1000 consecutive
episodes. We discovered that the number of pre-
training steps significantly impacts the ability to find
an acceptable policy for the “CartPole-v1” environ-
ment. Figure 2 illustrates this effect. It shows that the
agent pre-trained with 150000 iterations cannot bal-
ance the cart-pole for 500 steps per episode for 1000
consecutive episodes, which is the requirement for an
acceptable policy. This agent for trained for 10000
episodes before stopping without finding an accept-
able policy. In contrast, the agents pre-trained for
200000 and 250000 iterations both find an accept-
able policy. The main goal of this analysis was to
Figure 2: Along x-axis, the episode countdown to the stop-
page of the online training is plotted. Along y-axis, the
number of steps in an episode where the cart-pole remains
balanced is plotted. For the red curve that corresponds to
the experiment where the target network is used throughout
training, the countdown is started at the 3021
th
episode in
the online training phase. The other curves correspond to
different number pre-training steps before switching to the
online training phase. The orange curve, with 200000 pre-
training steps reaches an acceptable policy faster - at the
1159
th
episode, even without a target network.
demonstrate that an agent can find an acceptable pol-
icy without using a target network if it is first pre-
trained before continuing the training in online learn-
ing. We found such policies for both cases, where
we pre-trained for 200000 and 250000 steps, respec-
tively. Additionally, we observed that very long pre-
training has an adverse effect on the rate of conver-
gence within the online phase. For example, the best
performance was achieved when the number of pre-
training steps very limited to 200000 steps as opposed
to 250000. In fact, the former has the best rate of con-
vergence, find an acceptable policy in 1159 episodes,
bettering the rate of convergence of traditional DQN
with a target network - it needed 3021 episodes.
3.2 Comparing the Quality of the
Acceptable Policies Found
One method to compare the quality of the acceptable
policy found is to compare the rewards accumulated
within an episode. This is done in Figure 3. It com-
pares the traditional online training with three pre-
trained online training modes - 250000, 300000 and
350000 pre-training steps. While describing Figure 2,
we said that 200000 is the optimal number of pre-
training steps with respect to learning rate - it finds
the acceptable policy first. For this set of experiments,
we decided to pre-train for a longer time, since we
wanted to check the critical nature of stopping the of-
fline phase, particularly with respect to the quality of
the acceptable policy found. For example, suppose
we are conservative and have a very long pre-training
phase, can we find a good policy? Figure 3 shows that
good policies can be learnt in a stable manner, with-
ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods
442

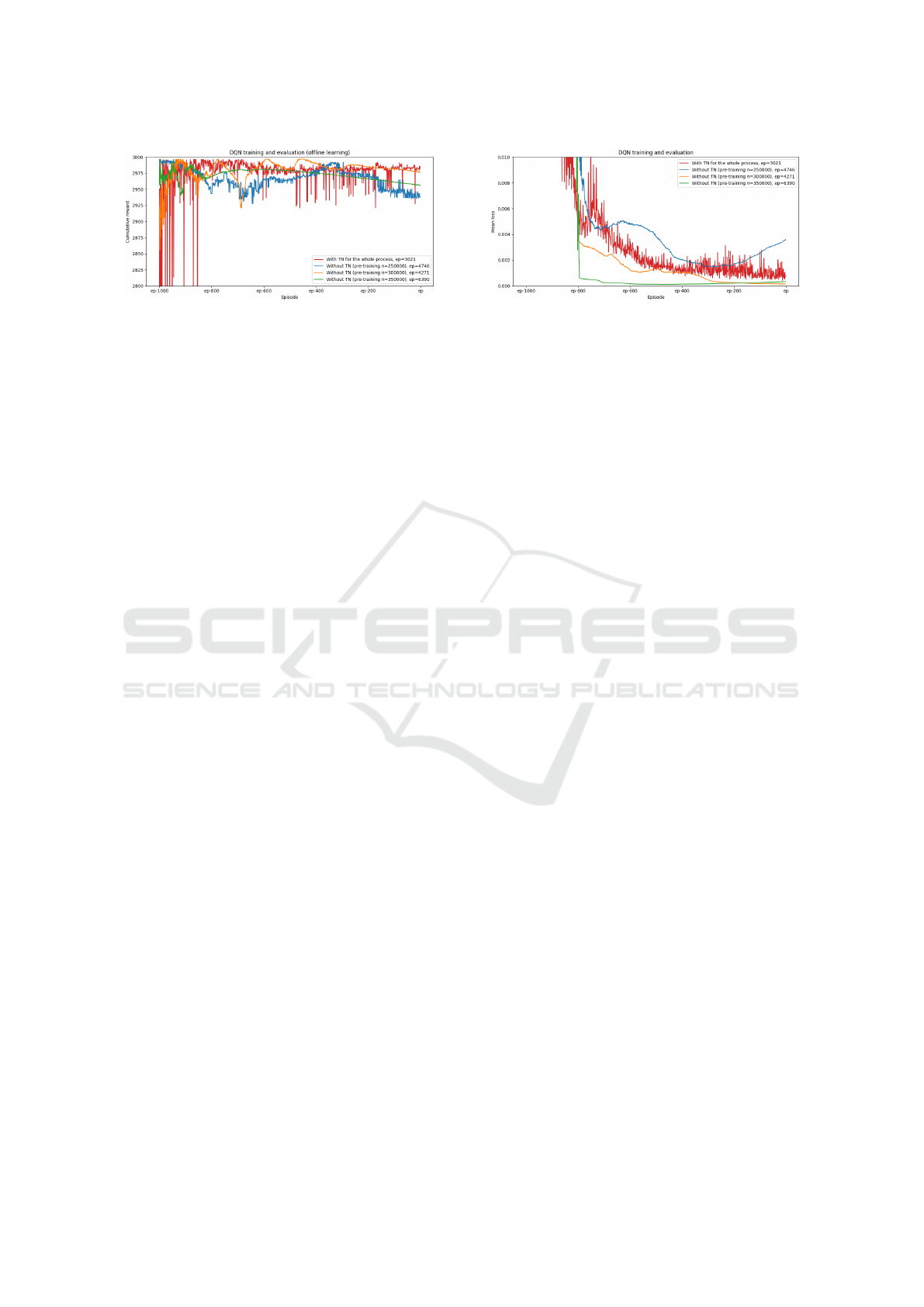
Figure 3: Like in the previous figure, along x-axis, the
episode countdown to the stoppage of the online training
is plotted. Along y-axis, we plot the cumulative rewards
per episode. The experiments corresponding to the pre-
trained online learning were repeated for 250000, 300000
and 350000 pre-training steps - beyond the optimal limit.
We wanted to study the criticality of choosing the right pre-
training duration. The red curve corresponds to the tradi-
tional online training with a target network. The orange
curve, corresponding to 300000 pre-training steps has a cu-
mulative reward that is comparable to traditional training.
It is poignant to observe that the cumulative rewards exhibit
very low variance, as compared to traditional training which
exhibits very high variance throughout training.
out a target network, provided the DQN is pre-trained
for a certain number of steps. Pre-training has the ad-
ditional advantageous, since it reduces variance dur-
ing training. Low variance is often associated with
low data consumption, hence we believe that elimi-
nating target networks also has a positive impact on
the amount of data needed to train a DQN.
Another method to compare the quality of the ac-
ceptable policies is by comparing the average loss per
episode. This is done in 4. The first thing to notice is
that the variance is lower for the agents trained with-
out a target network. Much like the plot with the re-
wards, the pre-trained online training is able to effec-
tively minimize the squared Bellman loss - the prin-
cipal aim in RL. From our various experiments we
conclude that the target network is redundant if we
pre-train an agent before the online learning phase.
We can discard the target network, but we may need
to determine the length of pre-training, which for now
is determined through trial and error.
4 CONCLUSIONS
We described a simple two phase training for DQN.
The aim of this study is to show that this eliminates
the need for a target network, thereby speeding up
training, in addition to greatly reducing variance. In
the first stage, we train the DQN in an offline man-
ner using a history of expert actions. In particular,
an experience replay buffer is filled with these sam-
ples. Then, for a certain number of pre-training steps,
Figure 4: This figure tells the same story as said by Figure 3,
from the perspective of loss instead of reward. Along x-
axis, the episode countdown to the stoppage of the online
training is plotted. Along y-axis, we plot the average loss
per episode.
a mini-batch is sampled from this buffer, and a loss
gradient is calculated to update the DQN. The usual
squared Bellman loss is minimized. This step differs
from the traditional method of using expert actions.
In literature, during pre-training, the DQN is trained
to maximize the chances of picking the expert actions.
In the second online phase, the DQN is trained to min-
imize the Bellman loss while interacting with an en-
vironment (simulator) - traditional method. However,
we did not use a target network at any stage of train-
ing.
We found that our pre-trained online training of
DQN greatly enhanced learning stability without the
need for a target network. Variance during training
was reduced, this reduced the training duration and
the amount of training data needed. The policy found
was as good, and in some cases better than, the one
found by training using a target network. The only
caveat being the pre-training duration. We observed
that the number of pre-training steps has an influence
on the rate of convergence during the online phase.
This duration, we believe, is problem dependent and
can be found through trial and error. While a short
pre-training phase leads to unstable learning, longer
than optimal pre-training still finds a good policy. The
optimality if only with respect to the rate of conver-
gence to this policy.
ACKNOWLEDGEMENTS
The research presented in this paper was conducted
when Lindstr
¨
om was working on his Masters the-
sis under the supervision of Ramaswamy (Lindstr
¨
om,
2024).
The work was carried out within the Data-driven
Latency-sensitive Mobile Services for a Digitalized
Society (DRIVE) project, which is partly funded by
the Knowledge Foundation of Sweden.
Pre-Training Deep Q-Networks Eliminates the Need for Target Networks: An Empirical Study
443

REFERENCES
Cruz Jr, G. V. d. l., Du, Y., and Taylor, M. E.
(2019). Pre-training Neural Networks with Human
Demonstrations for Deep Reinforcement Learning.
arXiv:1709.04083 [cs].
Hester, T., Vecerik, M., Pietquin, O., Lanctot, M., Schaul,
T., Piot, B., Horgan, D., Quan, J., Sendonaris, A.,
Dulac-Arnold, G., Osband, I., Agapiou, J., Leibo,
J. Z., and Gruslys, A. (2017). Deep Q-learning from
Demonstrations. arXiv:1704.03732 [cs].
Kim, S., Asadi, K., Littman, M., and Konidaris, G. (2019).
DeepMellow: Removing the Need for a Target Net-
work in Deep Q-Learning. In Proceedings of the
Twenty-Eighth International Joint Conference on Ar-
tificial Intelligence, pages 2733–2739, Macao, China.
International Joint Conferences on Artificial Intelli-
gence Organization.
Lindstr
¨
om, A. (2024). An empirical study of stability and
variance reduction in Deep Reinforcement Learning.
Dept. of Computer Science, Karlstad University.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing Atari with Deep Reinforcement
Learning. arXiv:1312.5602 [cs].
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller,
M., Fidjeland, A. K., Ostrovski, G., Petersen, S.,
Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-
maran, D., Wierstra, D., Legg, S., and Hassabis, D.
(2015). Human-level control through deep reinforce-
ment learning. Nature, 518(7540):529–533.
Philipp, G., Song, D., and Carbonell, J. G. (2018). GRA-
DIENTS EXPLODE - DEEP NETWORKS ARE
SHALLOW - RESNET EXPLAINED.
Ramaswamy, A., Bhatnagar, S., and Saxena, N. (2023).
A Framework for Provably Stable and Consis-
tent Training of Deep Feedforward Networks.
arXiv:2305.12125 [cs].
Ramaswamy, A. and H
¨
ullermeier, E. (2022). Deep q-
learning: Theoretical insights from an asymptotic
analysis. IEEE Transactions on Artificial Intelligence,
3(2):139–151.
Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep Re-
inforcement Learning with Double Q-Learning. Pro-
ceedings of the AAAI Conference on Artificial Intelli-
gence, 30(1).
Yang, G., Li, Y., Fei, D., Huang, T., Li, Q., and Chen, X.
(2021). DHQN: a Stable Approach to Remove Tar-
get Network from Deep Q-learning Network. In 2021
IEEE 33rd International Conference on Tools with Ar-
tificial Intelligence (ICTAI), pages 1474–1479, Wash-
ington, DC, USA. IEEE.
ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods
444