: Sparse-View 3D Object Reconstruction with a Hybrid Implicit

Initialization

Pragati Jaiswal

1,2

and Didier Stricker

1,2

RPTU - Technische Universit

at Kaiserslautern, Germany

DFKI – German Research Center for Artificial Intelligence, Germany

Keywords:

Object Reconstruction, 3D Reconstruction, Hybrid Implicit Initialization.

Abstract:

Accurate 3D object reconstruction is essential for various applications, including mixed reality and medicine.

Recent advancements in deep learning-based methods and implicit 3D modelling have signiﬁcantly enhanced

the accuracy of 3D object reconstruction. Traditional methods enable reconstruction from a limited number

of images, while implicit 3D modelling is proﬁcient at capturing ﬁne details and complex topologies. In this

paper, we present a novel pipeline for 3D object reconstruction that combines the strengths of both approaches.

Firstly, we use a 3D occupancy grid to generate a coarse 3D object from a few images. Secondly, we implement

a novel and effective sampling strategy to transform the coarse reconstruction into an implicit representation,

which is optimized to reduce computation power and training time. This sampling strategy also allows it

to be true to scale given actual camera intrinsic and extrinsic parameters. Finally, we reﬁne the implicit

representation and extract the 3D object mesh under a differentiable rendering scheme. Experiments on several

datasets demonstrate that our proposed approach can reconstruct accurate 3D objects and outperforms state-

of-the-art methods in terms of the Chamfer distance and Peak Signal-to-Noise Ratio metrics.

1 INTRODUCTION

The topic of 3D object reconstruction has received in-

creased attention due to the recent emergence of many

neural implicit representations. The ability to easily

reconstruct even photorealistic 3D objects is of sig-

niﬁcant interest for a wide ﬁeld of applications. This

is especially the case in the ﬁeld of virtual and aug-

mented reality. However, not all of these methods

produce an output that is compatible with standard

rendering engines. Some representations like neu-

ral radiance ﬁelds (Mildenhall et al., 2021) and voxel

grids (Fridovich-Keil et al., 2022) require a volume

rendering approach that can be very costly. In those

cases, it might not be possible to achieve real-time

rendering unless a mesh is extracted in a separate step.

Converting these representations in a separate step is,

however, computationally expensive and can reduce

the quality of the original reconstruction. Methods

that directly output a mesh are, therefore, preferable

as they do not require additional computations and re-

tain their level of quality.

In this work, we aim to reconstruct high-ﬁdelity

3D models of objects using only a sparse set of im-

ages. The implicit modelling is suitable for capturing

Figure 1: We propose HI

, a novel Hybrid Implicit Initial-

ization. Given sparse views, we aim to reconstruct a highly

accurate mesh of the object. In this ﬁgure, we show input

images and our 3D object reconstruction. It is clearly no-

ticeable that our reconstruction pipeline can maintain high-

frequency details.

high-frequency details. Meanwhile, a coarse mesh

makes the reconstruction from a few images possi-

ble. Motivated by this, we propose a novel 3D object

reconstruction pipeline HI

, combining the strengths

of implicit modelling and explicit coarse mesh recon-

struction. For this, we use a novel approach to create

a coarse reconstruction of the object from as few as

170

Jaiswal, P. and Stricker, D.

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization.

DOI: 10.5220/0013382000003905

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2025), pages 170-180

ISBN: 978-989-758-730-6; ISSN: 2184-4313

ﬁve images.

We then optimize this initial mesh using implicit

modelling via a neural rendering-based optimization

process. We propose a novel shell-constrained sam-

pling strategy to transfer the coarse reconstruction

into an implicit representation. Thanks to this shell,

we are able to sample only from the area close to the

object’s surface instead of sampling from all points

in the unit cube, as most approaches do (Park et al.,

2019; Tretschk et al., 2020). Using the sampled

Signed Distance Function (SDF) values, we initialize

a differentiable tetrahedral grid (Shen et al., 2021).

By combining the differentiable implicit representa-

tion with texture and lightning modelling (Munkberg

et al., 2022), we optimize the tetrahedral grid w.r.t.

the photometric reprojection error. Finally, we di-

rectly extract the object surface from the tetrahedral

grid without the expensive computational overhead.

We successfully lifted the implicit modelling to a 3D

reconstruction from sparse views using our pipeline.

We can summarize our main contributions as fol-

lows:

• We introduce an approach that combines clas-

sic 3D occupancy mapping and implicit 3D mod-

elling for 3D object reconstruction.

• We propose a novel shell-constrained sampling

strategy which helps in reducing the required

computational power and training time. In addi-

tion, it helps in generating a high-quality mesh

even with a limited number of images.

Extensive experiments demonstrate that our pipeline

can reconstruct a full 3D object with rich details using

only a few images. We also show that we outperform

State-Of-The-Art (SOTA) implicit 3D modelling ap-

proaches w.r.t. the Chamfer distance metric and Peak

Signal-to-Noise Ratio (PSNR) under different num-

bers of views.

2 RELATED WORK

2.1 Classical Methods

Multi-View Stereo (MVS) is a fundamental prob-

lem in 3D computer vision and has been exten-

sively researched. The classic approaches usually es-

timate the depth map through matching correspon-

dences across images (Pons et al., 2005; Kolmogorov

and Zabih, 2002; Goesele et al., 2006). However,

the matching quality heavily depends on the degree

of overlap in the neighbourhood images, which re-

quires a large number of views. Although such ap-

proaches have achieved a promising reconstruction

quality (Furukawa and Ponce, 2009; Galliani et al.,

2016; Sch

onberger et al., 2016), the dense match-

ing and the post-processing step for mesh genera-

tion (Kazhdan et al., 2006) are computationally ex-

pensive.

2.2 Explicit Representations

With the development of deep learning, MVS can eas-

ily become more feasible by implementing learning-

based components for the subtasks, such as feature

matching (Hartmann et al., 2017; Luo et al., 2019)

and depth fusion (Donne and Geiger, 2019; Riegler

et al., 2017). Furthermore, end-to-end deep learning

approaches are also proposed to directly reconstruct

objects from input images. A research branch recon-

structs the object in voxel-grids (Choy et al., 2016;

Kar et al., 2017; Yan et al., 2016). However, the

voxel-grid size grows cubically to maintain ﬁne de-

tails in the reconstruction. Moreover, the voxel rep-

resentation is incompatible with the standard render-

ing pipeline, limiting their applications in graphics.

Presenting object shapes as a mesh in the reconstruc-

tion is more memory efﬁcient. Nevertheless, most ap-

proaches assume a ﬁxed mesh topology (Wang et al.,

2018; Liu et al., 2019a; Kanazawa et al., 2018), which

makes those approaches only suitable for reconstruct-

ing objects with similar geometries.

2.3 Implicit Representations

A more memory-efﬁcient way is to represent the

object surface as neural implicit representations,

which can theoretically express the object surface

in an inﬁnite resolution with a ﬁxed memory de-

mand. SDF (Park et al., 2019) and occupancy

functions (Mescheder et al., 2019) are commonly

used as neural implicit representations. In multi-

view 3D reconstruction, neural implicit representa-

tions are mostly used jointly with differentiable ren-

dering (Jiang et al., 2020; Liu et al., 2020; Liu et al.,

2019b) to extract the surface point of each view.

Implicit Differentiable Renderer (IDR) (Yariv et al.,

2020) further combines the implicit representation

with the apprentice model that can differentiably ren-

der object views accounting for light effects. Thanks

to the differentiable modelling of object geometry and

appearance, IDR is able to reconstruct high-quality

object surfaces under 2D supervision only. How-

ever, IDR still relies on the computationally expen-

sive Marching Cubes algorithm (Lorensen and Cline,

1987) to extract the reconstructed object surface.

Instead, Deep Marching Tetrahedra (DMTet) (Shen

et al., 2021) proposes a novel 3D representation to re-

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization

171

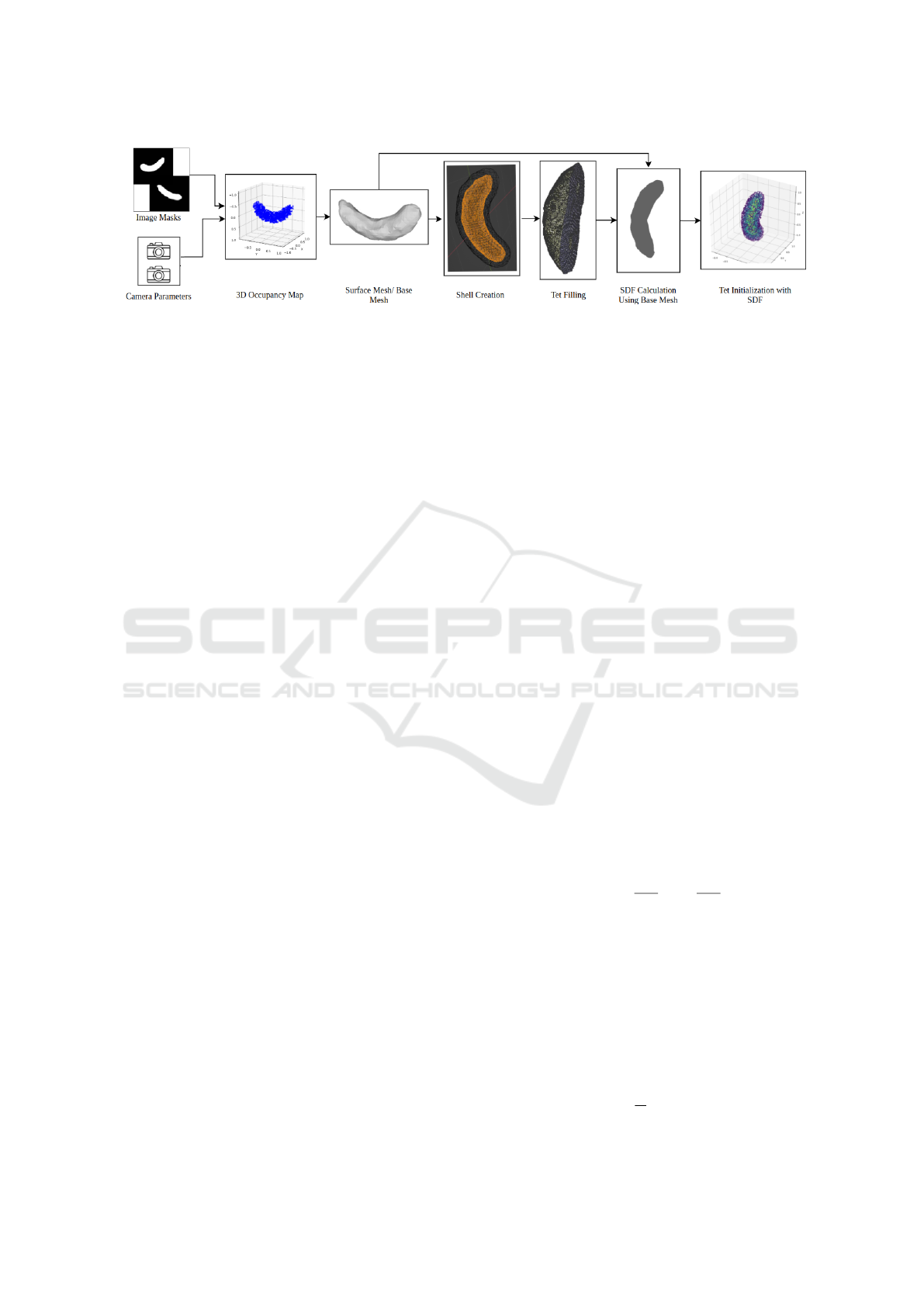
Figure 2: Hybrid Implicit Initialization (HI

). Our initialization approach starts from a sparse set of images to reconstruct a

coarse mesh using a 3D occupancy map. A shell is then constructed around the coarse mesh, which is ﬁlled with a tetrahedral

grid. Additionally, a Signed Distance Function (SDF) is created using the tetrahedral grid and coarse mesh.

construct the shape by a differentiable marching tetra-

hedra layer while keeping a fast inference rate. Nvd-

iffrec (Munkberg et al., 2022) implements a recon-

struction pipeline upon DMTet with additional mate-

rials and lighting modelling, which takes a step fur-

ther towards high-ﬁdelity 3D reconstruction from im-

ages. Neural volumes can also be seen as a 3D ob-

ject representation. With volumetric rendering, Neu-

ral Radiance Fields (NeRF) (Mildenhall et al., 2021)

and its follow-up work (Garbin et al., 2021; Martin-

Brualla et al., 2021; Pumarola et al., 2021; Reiser

et al., 2021; Wang et al., 2021; Wizadwongsa et al.,

2021; Yu et al., 2021; Zhang et al., 2020; Kellnhofer

et al., 2021) have shown great success in the area of

novel view synthesis. However, they are mainly fo-

cused on the optimization of object appearance. The

ambiguity in the volumetric rendering limits the su-

pervision of the object geometry (Zhang et al., 2020).

Although one can also extract object surfaces from

such methods, the reconstructed geometry is usually

not satisﬁable.

Our approach builds on the advances of DMTet

and Nvdiffrec through a clever hybrid initialization

that takes advantage of explicit and implicit represen-

tations.

3 METHOD

We present a method for 3D object reconstruction that

utilizes a sparse set of images of an arbitrary object.

Starting with a minimum of ﬁve input images, accom-

panied by masks and camera parameters, we gener-

ate a 3D occupancy map of the object. This occu-

pancy map serves as the foundation for reconstructing

a coarse mesh, which forms the initial structure of our

method.

Next, we reﬁne the reconstruction by creating a

shell around the coarse mesh and ﬁlling it with a

tetrahedral grid. Unlike arbitrary shapes, the shell-

constrained tetrahedral grid closely approximates the

object’s structure, providing a more accurate starting

point for further optimization.

The tetrahedral mesh is initialized with SDF val-

ues derived from the coarse mesh. Using this ini-

tialized mesh, we employ the Nvdiffrec’s DMTet

pipeline to optimize the reconstruction. During each

optimization iteration, the tetrahedral mesh is differ-

entiably rendered, allowing us to compute the loss be-

tween the rendered image and the ground truth inputs.

3.1 Initialization Approach

In the following, we detail the steps of our initializa-

tion approach, summarized in Figure 2.

3.1.1 Coarse Mesh

Given a set of posed colour images I = {I

, I

, . . . , I

}

with corresponding binary object masks M =

, M

, . . . , M

} and known camera parameters C =

, C

, . . . , C

}, we estimate a coarse occupancy

map of the object using a space carving algorithm

(Kutulakos and Seitz, 2000).

A set of random 3D points P = {p

, p

, . . . , p

where p

= (x

, y

, z

), is generated within the 3D space

enclosing the object. Each point is projected onto the

2D image plane of every view n ∈ [1, N] using the

camera projection function P

, deﬁned as:

u, v = P

, C

) =



+ c



, (1)

where f

, f

are the focal lengths, and c

, c

are the

principal points.

For each projected point, we check if its projection

(u, v) lies within the object mask M

(u, v):

) =

(

1 if M

(u, v) = 1,

0 otherwise.

(2)

The object’s ﬁnal occupancy score is determined by

aggregating o

) across all views:

O(p

) =

∑

n=1

) (3)

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

172

Points with O(p

) ≥ τ, where τ is a threshold (e.g.,

τ = 0.5), are retained as part of the object’s visual hull.

An alpha shape A

is computed from the retained

points, representing the coarse mesh. The alpha shape

is deﬁned as the smallest triangulation enclosing the

points such that all edges have a length ≤ α. The

choice of α is inﬂuenced by the approximate spac-

ing between the points d

mean

, which depends on the

density of the initialized point cloud.

α ≈ c · d

mean

(4)

where c is a scaling factor typically in range 1.5 ≤

c ≤ 3, depending on desired granularity. This shape

approximates the object’s geometry and provides a

coarse mesh for subsequent steps.

3.1.2 Tetrahedral Mesh

Using the coarse mesh A

, we generate a tetrahedral

mesh T using the Quartet framework (Bridson and

Doran, 2014). Quartet employs an isosurface stuff-

ing algorithm (Shewchuk, 1998), which generates a

tetrahedral grid from a deﬁned boundary.

Instead of generating a tetrahedral grid within a

unit cube, we focus mesh generation on the near-

surface regions of the coarse mesh.

A conforming shell S

with thickness δ is con-

structed around A

= {q | q ∈ R

, d(q, A

) ≤

}, (5)

where d(q, A

) is the Euclidean distance from q to

the nearest point on A

The shell S

serves as the input boundary for the

Quartet framework, ensuring that the tetrahedral mesh

T aligns closely with the object’s surface geometry.

3.1.3 Signed Distance Function (SDF)

To improve convergence and guide optimization, we

initialize the tetrahedral mesh with SDF values de-

rived from the coarse mesh.

For each vertex v

∈ T , the SDF value is computed

as:

SDF(v

) = sgn(v

) · min

p∈A

∥v

− p∥

, (6)

where sgn(v

) = −1 if v

is inside the coarse mesh and

+1 otherwise.

The computed SDF values initialize the tetrahe-

dral grid, encoding proximity to the object’s surface.

This initialization provides:

• Improved Geometry Awareness: The optimiza-

tion starts with a spatially informed structure.

• Faster Convergence: A better initial conﬁgura-

tion reduces the number of iterations required for

optimization.

By combining these mathematically grounded

steps, our initialization approach achieves robust and

efﬁcient 3D object reconstruction, even with sparse

input data. The method ensures high ﬁdelity while

maintaining computational efﬁciency.

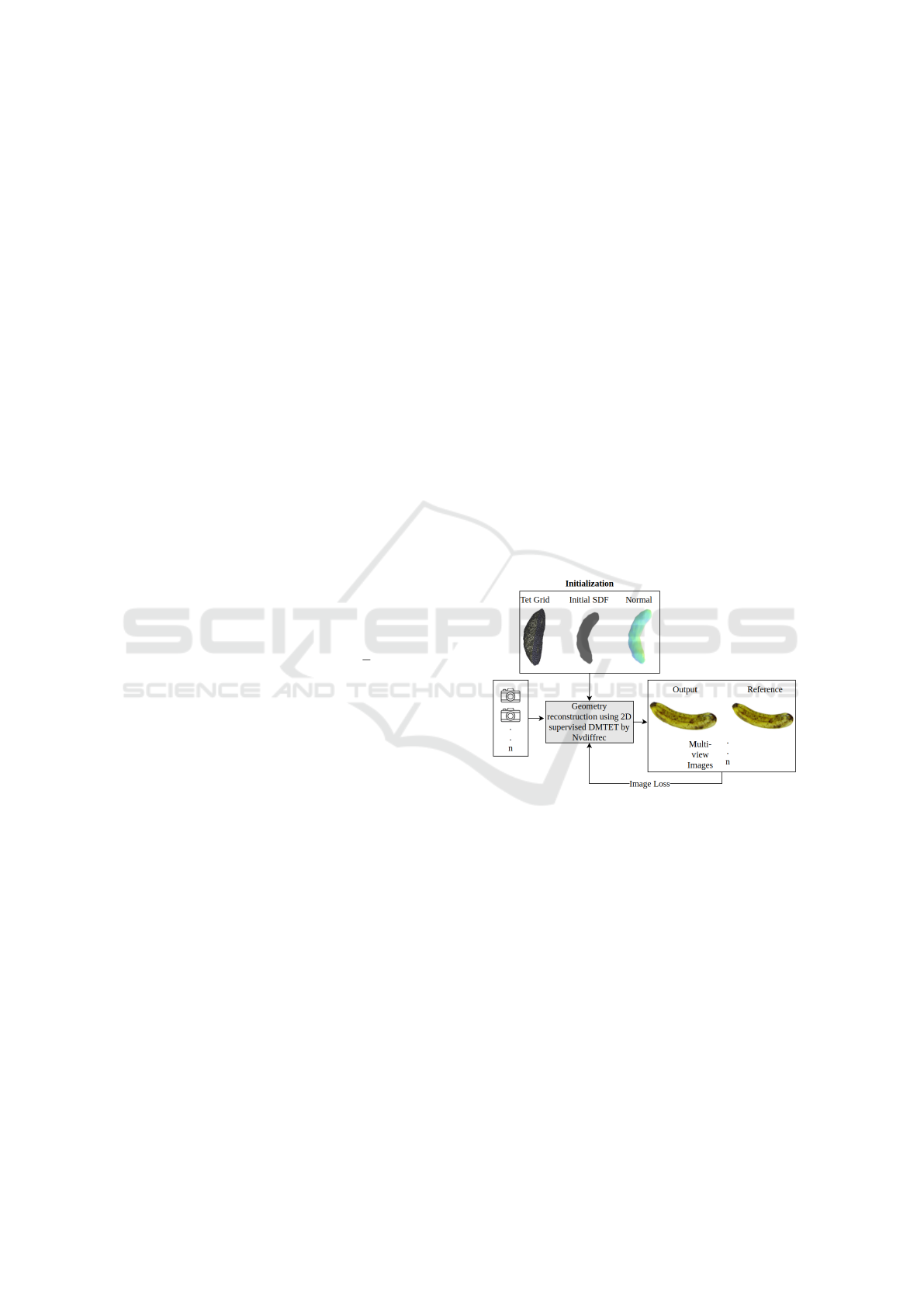
3.2 3D Reconstruction

The next stage focuses on reﬁning and optimizing

the mesh geometry to align with the input images,

thereby improving the overall representation of the

reconstructed object. A visualization of this recon-

struction pipeline is provided in Figure. 3.

To achieve this, we utilize the DMTet framework,

integrated with 2D supervision from Nvdiffrec. This

integration enables efﬁcient optimization of the mesh

geometry. Unlike other approaches such as IDR,

which treat geometry and material properties as sep-

arate components, Nvdiffrec jointly optimizes geom-

etry, materials, and lighting. This simultaneous opti-

mization enhances the alignment between the recon-

structed shape and the image data, leading to a more

robust reconstruction process.

Figure 3: Reconstruction pipeline with HI

: Multiview im-

ages and their corresponding camera parameters serve as

input. Our initialization approach is used to enhance the

DMTet framework, supervised by Nvdiffrec, for improved

3D object reconstruction.

3.2.1 Optimization Process

During each iteration of the optimization, the march-

ing tetrahedral layer is converted into a surface mesh

representation. This surface mesh is rendered using

a differentiable rasterizer, utilizing the provided cam-

era parameters and viewpoints. The rendered output

is compared against the ground truth image data to

compute a loss function in the image space. This loss

is backpropagated through the optimization pipeline,

enabling updates to the surface mesh embedded in the

implicit ﬁeld.

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization

173

The iterative reﬁnement involves two key compo-

nents:

• Vertex Adjustments: The positions of vertices

within the tetrahedral grid are updated to improve

the alignment of the mesh with the object’s true

geometry.

• SDF Updates: The SDF values associated with

the tetrahedral mesh are also reﬁned, ensuring the

implicit representation more accurately encodes

the object’s shape.

By integrating our SDF-derived initialization, the

DMTet framework begins optimization from a well-

informed starting point. This initialization incorpo-

rates spatial information about the object’s geometry,

leading to faster convergence and improved accuracy.

The SDF initialization reduces the dependency on ex-

tensive input data, allowing our method to produce

high-quality 3D reconstructions with a sparse set of

input images.

This combination of SDF-based initialization and

joint optimization of geometry, materials, and lighting

ensures the reconstructed 3D mesh achieves a high

level of ﬁdelity, even in scenarios with limited input.

4 EXPERIMENTS

4.1 Dataset

To evaluate the performance and versatility of our

proposed method, we utilized the OmniObject3D

(Wu et al., 2023) dataset and a synthetic face dataset

created speciﬁcally for this study. These datasets

were chosen to ensure a robust assessment across a

diverse range of object types, including both general

and highly specialized geometries.

4.1.1 OmniObject3D

The OmniObject3D dataset provides an extensive col-

lection of object categories with varying shapes and

complexities. It serves as a benchmark for testing our

method’s capability to reconstruct a wide variety of

objects, from simple to highly intricate geometries.

By leveraging this dataset, we validate the robustness

and generalizability of our approach across general

object types.

4.1.2 Synthetic Face Dataset

To further demonstrate the ﬂexibility of our method,

particularly for objects with intricate geometry, we

developed a synthetic face dataset. This dataset was

(a) Starting Position (b) Ending Position

Figure 4: Visualization of the camera arc: (a) Starting po-

sition of the camera; (b) Ending position of the camera,

demonstrating the range used in the experiments.

created by rendering 3D models using CharacterCre-

ator4 (Inc., 2022) in Blender (Community, 2018). The

dataset includes three distinct 3D models:

• One female model.

• Two male models, one with hair and the other

bald, to evaluate the reconstruction performance

across different head geometries, including varia-

tions with long, short, or no hair.

To increase the difﬁculty and simulate diverse

viewing conditions, we rendered images along a cam-

era arc spanning −90

◦

to +90

◦

. Figure 4 shows the

starting and ending position of the camera’s arc. All

images were generated under consistent lighting and

rendering settings to maintain controlled experimen-

tal conditions.

4.2 Evaluation Setup

By combining the OmniObject3D dataset with the

synthetic face dataset, we comprehensively evaluate

our method’s ability to handle diverse object cate-

gories and geometries. OmniObject3D ensures the

general applicability of the method, while the syn-

thetic face dataset tests its robustness on highly de-

tailed and geometrically complex objects such as hu-

man faces.

We maintained consistent evaluation parameters

for all methods we tested. The resultant 3D mesh is

aligned with the ground truth mesh using landmarks

and then ﬁne-tuned using Trimesh (Dawson-Haggerty

et al., ) implementation of the Iterative Closest Point

(ICP) (Besl and McKay, 1992). Our comparison of

results against other methods was done by using uni-

directional Chamfer distance.

Our evaluation involved comparing the 3D mesh

predictions from Nvdiffrec and IDR trained on the

same dataset across different views. For the Om-

niObject3D dataset, we had a full dataset (100 im-

ages) as well as randomly chosen subsets contain-

ing 20, 10, and 5 images. To ensure a fair compari-

son, the same subsets were used for evaluating each

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

174

method. We used 19, 13, 9, and 5 images for the

face dataset. This comprehensive comparison allowed

us to understand how the performance of Nvdiffrec,

IDR and our method trained on identical datasets,

varied under different training datasets and number

of views. Additionally, we conducted a comparative

analysis between the outcomes produced by Nvdiffrec

and our initialization strategy. This comparison aimed

to assess the convergence of the two methods. We

achieved this by contrasting the Peak Signal-to-Noise

Ratio (PSNR) and the Mean Squared Loss (MSE) cal-

culated between the input image and the rendered im-

age at different numbers of training epochs. This eval-

uation allowed us to gauge the effectiveness of our

initialization approach in relation to Nvdiffrec’s per-

formance.

4.3 Ablation Study

Figure 5: Visual comparison of 3D reconstructions with dif-

ferent tet sizes. As the tet size increases, the level of detail

in the reconstructed surface changes, with a ﬁner tet size

(0.003) capturing sharper geometric details, while a larger

tet size (0.007) results in smoother reconstructions.

We perform an ablation study on the size of tets used

for ﬁlling the shell created. We start by ﬁlling the shell

with a tet size of 0.007, 0.005, and 0.003 respectively.

We observe that the smaller the size of the tet grid

used for the generation, the higher the high-frequency

detail which can be observed in Figure 5, especially if

we look closer at the eye region and hair.

However, we also note that smaller tet sizes result

in noisier and less smooth surfaces in the 3D model,

potentially detracting from the overall realism. Con-

versely, while larger tet sizes, such as 0.007, produce

smoother surfaces, they lack the ﬁner detail captured

by smaller tet sizes.

The results as visualized in Figure 6, further sup-

port this observation. At a tet size of 0.005, we ob-

serve an optimal balance between PSNR and MSE,

indicating that it achieves a good trade-off between

capturing sufﬁcient detail and maintaining surface

Figure 6: Effect of tet size on PSNR and MSE. The blue

curve represents PSNR values (left axis), and the red curve

represents MSE values (right axis).

smoothness. This balance makes 0.005 an ideal

choice for maintaining both visual quality and real-

ism in the reconstructed model.

4.4 Quantitative Results

4.4.1 HI

vs Nvdiffrec

In Figure 7, it is evident that HI

achieves conver-

gence with only a few training iterations. This is in-

dicated not only by the better PSNR and MSE val-

ues but also by the clear convergence in the graph.

The number of training iterations required is directly

related to the training time, and the proposed re-

construction pipeline requires less training time than

Nvdiffrec with the standard random tet grid initializa-

tion for 3D object reconstruction.

(a) MSE ↓ vs No. of iterations

(b) PSNR ↑ vs No. of iterations

Figure 7: Comparison between Nvdiffrec with standard ran-

dom tet grid initialization and HI

. HI

converges better

than Nvdiffrec with standard random tet grid initialization.

4.4.2 HI

vs All

We compare HI

against Nvdiffrec and IDR across

diverse 3D object reconstruction tasks. Table 1

shows that HI

consistently outperforms all methods

in terms of Chamfer distance across different datasets

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization

175

Table 1: Chamfer distance ↓ comparison for OmniObject3D and face datasets across various number of views. The bolded

values indicate the best performance for each dataset and view count combination.

Anise Banana Face-1 Face-2 Face-3

Views 5 10 20 100 5 10 20 100 5 9 13 19 5 9 13 19 5 9 13 19

Nvdiffrec 0.019 0.016 0.015 0.014 0.018 0.014 0.014 0.014 0.011 0.009 0.009 0.009 0.012 0.011 0.012 0.011 0.012 0.011 0.011 0.011

IDR 0.022 0.013 0.009 0.005 0.006 0.005 0.006 0.004 0.025 0.025 0.024 0.024 0.042 0.029 0.026 0.030 0.029 0.029 0.029 0.029

0.008 0.006 0.005 0.004 0.005 0.004 0.004 0.001 0.008 0.008 0.008 0.008 0.010 0.010 0.010 0.010 0.010 0.010 0.010 0.010

Nvdiffrec

Figure 8: Convergence of 3D reconstruction in 100 iterations with different numbers of views, using Nvdiffrec vs. HI

and numbers of input views.

achieves the lowest Chamfer distance across

all object categories, with smaller values indicating

better performance. Notably, it excels with sparse

input (e.g., 5 views), delivering signiﬁcantly lower

Chamfer distances than IDR and Nvdiffrec, demon-

strating its efﬁciency when there is limited data avail-

able.

4.5 Qualitative Results

4.5.1 HI

vs Nvdiffrec

Figure 8 and Figure 9 present a visual comparison of

the convergence and accuracy of 3D reconstruction

using different numbers of views with the Nvdiffrec

and HI

methods. Figure 8 shows the progression

of reconstruction over 100 iterations, comparing the

output, reference, and normal. While the quality of

Nvdiffrec improves with more views, HI

achieves a

high level of detail and accuracy, even with few views.

This demonstrates that HI

can achieve reliable re-

constructions, outperforming Nvdiffrec in terms of

convergence and model accuracy, particularly when

fewer views are available. Figure 9 further illustrates

this comparison by showing the reconstructed models

alongside the ground truth. The green and red circles

highlight areas showing that HI

produces higher de-

tail and can achieve this with limited views. Together,

these ﬁgures emphasize the robustness of HI

in gen-

erating accurate 3D reconstructions with limited input

views.

4.5.2 HI

vs All

Figure 10 provides a visual representation of the re-

construction quality achieved by Nvdiffrec, IDR, and

, along with their corresponding Chamfer distance

values. The comparison clearly highlights the supe-

rior performance of HI

, as it consistently achieves

lower Chamfer distance values across varying num-

bers of input views. While both Nvdiffrec and IDR

show improvement as the number of views increases,

maintains high reconstruction quality even with

minimal input views. This demonstrates the robust-

ness and scalability of HI

in handling diverse 3D re-

construction scenarios, particularly when input views

are limited. Furthermore, HI

exhibits better struc-

tural preservation and detail ﬁdelity, outperforming

the competing methods across all tested conﬁgura-

tions.

Figure 11 further supports this observation

by showcasing the reconstructed models for each

method, colour-coded based on Chamfer distance.

The visual comparison clearly shows that HI

pro-

duces the highest quality reconstructions, with signif-

icantly lower Chamfer distance values and fewer arti-

facts compared to Nvdiffrec and IDR. Notably, when

the number of input views is minimal, HI

main-

tains superior accuracy and detail preservation, out-

performing the other methods. These results demon-

strate that HI

delivers cleaner and more precise re-

constructions, making it highly effective for real-

world scenarios with sparse data.

5 CONCLUSION

In this work, we propose a novel pipeline that en-

ables highly accurate 3D object reconstruction from

a sparse set of images. We introduce a novel shell-

sampling strategy that transforms the coarse recon-

struction into an implicit representation, allowing

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

176

Figure 9: Visual comparison of 3D reconstructions using HI

and Nvdiffrec with varying numbers of views. The reconstructed

models are shown alongside the ground truth, with green and red circles indicating areas of high accuracy and noticeable

discrepancies, respectively. HI

consistently preserves ﬁne details and maintains high accuracy, even with few views.

Figure 10: Qualitative comparison of 3D mesh reconstructions and Chamfer distance across different numbers of views (5,

10, 20, and 100) for OmniObject3D dataset. Results demonstrate that HI

achieves more accurate reconstructions compared

to Nvdiffrec and IDR especially when limited views are available (5 or 10 images).

for further optimization by neural implicit render-

ing. Through our experiments, we demonstrate the

effectiveness of our sampling strategy, which consis-

tently outperforms state-of-the-art 3D reconstruction

approaches across different multi-view setups. We

believe our approach is not limited to only the Nvd-

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization

177

Figure 11: Qualitative comparison of Chamfer distance across different numbers of views (5, 9, 13, and 19) for face dataset.

We can clearly see that for 5 images, Nvdiffrec did not converge, while HI

produced highly accurate results, outperforming

both Nvdiffrec and IDR.

iffrec pipeline but can also be integrated into other

methods. Looking ahead, we aim to further improve

our pipeline to enable accurate 3D reconstruction with

even fewer input images and integrate our initializa-

tion approach with other pipelines.

ACKNOWLEDGEMENT

This work was co-funded by the European Union

under Horizon Europe, grant number 101092889,

project SHARESPACE. We sincerely thank Dr.

Bernd Krolla, Dr. Johannes K

ohler, and Yongzhi Su

for their mentorship and invaluable support through-

out this research. We also extend our gratitude to Dr.

Jason Rambach for his assistance in providing con-

structive feedback during the writing process.

REFERENCES

Besl, P. and McKay, N. D. (1992). A method for registration

of 3-d shapes. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 14(2):239–256.

Bridson, R. and Doran, C. (2014). Quartet: A tetra-

hedral mesh generator that does isosurface stuff-

ing with an acute tetrahedral tile. https://github.

com/crawforddoran/quartet.

Choy, C. B., Xu, D., Gwak, J., Chen, K., and Savarese,

S. (2016). 3d-r2n2: A uniﬁed approach for single

and multi-view 3d object reconstruction. In Computer

Vision–ECCV 2016: 14th European Conference, Am-

sterdam, The Netherlands, October 11-14, 2016, Pro-

ceedings, Part VIII 14, pages 628–644. Springer.

Community, B. O. (2018). Blender - a 3D modelling and

rendering package. Blender Foundation, Stichting

Blender Foundation, Amsterdam.

Dawson-Haggerty et al. trimesh.

Donne, S. and Geiger, A. (2019). Learning non-volumetric

depth fusion using successive reprojections. In Pro-

ceedings of the IEEE/CVF Conference on Computer

Vision and Pattern Recognition, pages 7634–7643.

Fridovich-Keil, S., Yu, A., Tancik, M., Chen, Q., Recht,

B., and Kanazawa, A. (2022). Plenoxels: Radiance

ﬁelds without neural networks. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 5501–5510.

Furukawa, Y. and Ponce, J. (2009). Accurate, dense, and ro-

bust multiview stereopsis. IEEE transactions on pat-

tern analysis and machine intelligence, 32(8):1362–

1376.

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

178

Galliani, S., Lasinger, K., and Schindler, K. (2016).

Gipuma: Massively parallel multi-view stereo recon-

struction. Publikationen der Deutschen Gesellschaft

ur Photogrammetrie, Fernerkundung und Geoinfor-

mation e. V, 25(361-369):2.

Garbin, S. J., Kowalski, M., Johnson, M., Shotton, J., and

Valentin, J. (2021). Fastnerf: High-ﬁdelity neural ren-

dering at 200fps. In Proceedings of the IEEE/CVF

International Conference on Computer Vision, pages

14346–14355.

Goesele, M., Curless, B., and Seitz, S. M. (2006). Multi-

view stereo revisited. In 2006 IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion (CVPR’06), volume 2, pages 2402–2409. IEEE.

Hartmann, W., Galliani, S., Havlena, M., Van Gool, L., and

Schindler, K. (2017). Learned multi-patch similarity.

In Proceedings of the IEEE international conference

on computer vision, pages 1586–1594.

Inc., R. (2022). Character Creator 4. Version 4.0.

Jensen, R., Dahl, A., Vogiatzis, G., Tola, E., and Aanæs,

H. (2014). Large scale multi-view stereopsis evalua-

tion. In 2014 IEEE Conference on Computer Vision

and Pattern Recognition, pages 406–413. IEEE.

Jiang, Y., Ji, D., Han, Z., and Zwicker, M. (2020). Sdfd-

iff: Differentiable rendering of signed distance ﬁelds

for 3d shape optimization. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 1251–1261.

Kanazawa, A., Tulsiani, S., Efros, A. A., and Malik, J.

(2018). Learning category-speciﬁc mesh reconstruc-

tion from image collections. In Proceedings of the

European Conference on Computer Vision (ECCV),

pages 371–386.

Kar, A., H

ane, C., and Malik, J. (2017). Learning a multi-

view stereo machine. Advances in neural information

processing systems, 30.

Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Pois-

son surface reconstruction. In Proceedings of the

fourth Eurographics symposium on Geometry pro-

cessing, volume 7, page 0.

Kellnhofer, P., Jebe, L. C., Jones, A., Spicer, R., Pulli, K.,

and Wetzstein, G. (2021). Neural lumigraph render-

ing. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

4287–4297.

Kolmogorov, V. and Zabih, R. (2002). Multi-camera

scene reconstruction via graph cuts. In Computer

Vision—ECCV 2002: 7th European Conference on

Computer Vision Copenhagen, Denmark, May 28–31,

2002 Proceedings, Part III 7, pages 82–96. Springer.

Kutulakos, K. N. and Seitz, S. M. (2000). A theory of shape

by space carving. International journal of computer

vision, 38:199–218.

Liu, S., Li, T., Chen, W., and Li, H. (2019a). Soft rasterizer:

A differentiable renderer for image-based 3d reason-

ing. In Proceedings of the IEEE/CVF International

Conference on Computer Vision, pages 7708–7717.

Liu, S., Saito, S., Chen, W., and Li, H. (2019b). Learn-

ing to infer implicit surfaces without 3d supervision.

Advances in Neural Information Processing Systems,

32.

Liu, S., Zhang, Y., Peng, S., Shi, B., Pollefeys, M., and Cui,

Z. (2020). Dist: Rendering deep implicit signed dis-

tance function with differentiable sphere tracing. In

Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition, pages 2019–

2028.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

ACM siggraph computer graphics, 21(4):163–169.

Luo, K., Guan, T., Ju, L., Huang, H., and Luo, Y. (2019).

P-mvsnet: Learning patch-wise matching conﬁdence

aggregation for multi-view stereo. In Proceedings of

the IEEE/CVF International Conference on Computer

Vision, pages 10452–10461.

Martin-Brualla, R., Radwan, N., Sajjadi, M. S., Barron,

J. T., Dosovitskiy, A., and Duckworth, D. (2021). Nerf

in the wild: Neural radiance ﬁelds for unconstrained

photo collections. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion, pages 7210–7219.

Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S.,

and Geiger, A. (2019). Occupancy networks: Learn-

ing 3d reconstruction in function space. In Proceed-

ings IEEE Conf. on Computer Vision and Pattern

Recognition (CVPR).

Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T.,

Ramamoorthi, R., and Ng, R. (2021). Nerf: Repre-

senting scenes as neural radiance ﬁelds for view syn-

thesis. Communications of the ACM, 65(1):99–106.

Munkberg, J., Hasselgren, J., Shen, T., Gao, J., Chen, W.,

Evans, A., M

uller, T., and Fidler, S. (2022). Extract-

ing triangular 3d models, materials, and lighting from

images. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

8280–8290.

Park, J. J., Florence, P., Straub, J., Newcombe, R., and

Lovegrove, S. (2019). Deepsdf: Learning continu-

ous signed distance functions for shape representa-

tion. In Proceedings of the IEEE/CVF conference on

computer vision and pattern recognition, pages 165–

174.

Pons, J.-P., Keriven, R., and Faugeras, O. (2005). Mod-

elling dynamic scenes by registering multi-view im-

age sequences. In 2005 IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition

(CVPR’05), volume 2, pages 822–827. IEEE.

Pumarola, A., Corona, E., Pons-Moll, G., and Moreno-

Noguer, F. (2021). D-nerf: Neural radiance ﬁelds

for dynamic scenes. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion, pages 10318–10327.

Reiser, C., Peng, S., Liao, Y., and Geiger, A. (2021). Kilo-

nerf: Speeding up neural radiance ﬁelds with thou-

sands of tiny mlps. In Proceedings of the IEEE/CVF

International Conference on Computer Vision, pages

14335–14345.

Riegler, G., Ulusoy, A. O., Bischof, H., and Geiger, A.

(2017). Octnetfusion: Learning depth fusion from

HIÂš: Sparse-View 3D Object Reconstruction with a Hybrid Implicit Initialization

179

data. In 2017 International Conference on 3D Vision

(3DV), pages 57–66. IEEE.

Sch

onberger, J. L., Zheng, E., Frahm, J.-M., and Pollefeys,

M. (2016). Pixelwise view selection for unstructured

multi-view stereo. In Computer Vision–ECCV 2016:

14th European Conference, Amsterdam, The Nether-

lands, October 11-14, 2016, Proceedings, Part III 14,

pages 501–518. Springer.

Shen, T., Gao, J., Yin, K., Liu, M.-Y., and Fidler, S. (2021).

Deep marching tetrahedra: a hybrid representation for

high-resolution 3d shape synthesis. Advances in Neu-

ral Information Processing Systems, 34:6087–6101.

Shewchuk, J. R. (1998). An introduction to the conju-

gate gradient method without the agonizing pain. In

Proceedings of the 7th International Conference on

Meshing Roundtable, Meshing Roundtable, pages 3–

17, Albuquerque, NM, USA. Sandia National Labora-

tories.

Tretschk, E., Tewari, A., Golyanik, V., Zollh

ofer, M.,

Stoll, C., and Theobalt, C. (2020). Patchnets: Patch-

based generalizable deep implicit 3d shape represen-

tations. In Computer Vision–ECCV 2020: 16th Euro-

pean Conference, Glasgow, UK, August 23–28, 2020,

Proceedings, Part XVI 16, pages 293–309. Springer.

Wang, N., Zhang, Y., Li, Z., Fu, Y., Liu, W., and Jiang, Y.-

G. (2018). Pixel2mesh: Generating 3d mesh models

from single rgb images. In Proceedings of the Euro-

pean conference on computer vision (ECCV), pages

52–67.

Wang, Z., Wu, S., Xie, W., Chen, M., and Prisacariu, V. A.

(2021). Nerf–: Neural radiance ﬁelds without known

camera parameters. arXiv preprint arXiv:2102.07064.

Wizadwongsa, S., Phongthawee, P., Yenphraphai, J., and

Suwajanakorn, S. (2021). Nex: Real-time view syn-

thesis with neural basis expansion. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 8534–8543.

Wu, T., Zhang, J., Fu, X., Wang, Y., Ren, J., Pan, L., Wu,

W., Yang, L., Wang, J., Qian, C., et al. (2023). Om-

niobject3d: Large-vocabulary 3d object dataset for re-

alistic perception, reconstruction and generation. In

Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition, pages 803–814.

Yan, X., Yang, J., Yumer, E., Guo, Y., and Lee, H. (2016).

Perspective transformer nets: Learning single-view

3d object reconstruction without 3d supervision. Ad-

vances in neural information processing systems, 29.

Yariv, L., Kasten, Y., Moran, D., Galun, M., Atzmon, M.,

Ronen, B., and Lipman, Y. (2020). Multiview neural

surface reconstruction by disentangling geometry and

appearance. Advances in Neural Information Process-

ing Systems, 33:2492–2502.

Yu, A., Li, R., Tancik, M., Li, H., Ng, R., and Kanazawa,

A. (2021). Plenoctrees for real-time rendering of neu-

ral radiance ﬁelds. In Proceedings of the IEEE/CVF

International Conference on Computer Vision, pages

5752–5761.

Zhang, K., Riegler, G., Snavely, N., and Koltun, V. (2020).

Nerf++: Analyzing and improving neural radiance

ﬁelds. arXiv preprint arXiv:2010.07492.

APPENDIX

The DTU (Jensen et al., 2014) dataset is a well-known

benchmark for 3D reconstruction, notable for its di-

versity in object types and challenging imaging con-

ditions. Many images in the dataset capture objects

partially only, resulting in incomplete views that can

complicate reconstruction tasks.

Table 2 provides a quantitative comparison of

PSNR values for two scans (scan40 and scan65)

across different numbers of input views. HI

consis-

tently outperforms both IDR and Nvdiffrec, achieving

the highest PSNR values in every conﬁguration. Its

performance remains strong, especially with sparse

input (e.g., 5 views), and delivers the best results for

all tested view counts.

Table 2: PSNR value ↑ for DTU dataset across the different

number of views. The bolded values highlight the best per-

formance for each view count and dataset combination.

scan40 scan65

IDR 21.87 21.84 23.03 25.11 21.33 22.08 20.27 23.21

Nvdiffrec 22.27 23.25 23.73 23.88 20.3 20.55 21.5 21.57

24.05 24.65 25.09 25.631 23.32 24.8 25.05 26.68

Figure 12: Results for the DTU dataset with 10 random im-

ages trained for 2000 iterations. We can see clearly we are

able to produce results close to the ground truth.

Figure 12 visually compares reconstructions pro-

duced by HI

against the ground truth. Using only

10 input images and training for 2000 iterations, HI

achieves results that closely resemble the ground truth

despite the challenges posed by the dataset. These

results underscore HI

’s ability to generate high-

quality reconstructions even under constrained con-

ditions, reafﬁrming its efﬁciency.

ICPRAM 2025 - 14th International Conference on Pattern Recognition Applications and Methods

180