Manipulating Gloss of Real Objects Under Omnidirectional Lighting

Yuki Miyoshi

, Ryo Kawahara

2 a

and Takahiro Okabe

3 b

Department of Artiﬁcial Intelligence, Kyushu Institute of Technology, Iizuka, Fukuoka 820-8502, Japan

Graduate School of Informatics, Kyoto University, Sakyo-ku, Kyoto 606-8501, Japan

Information Technology Track, Okayama University, Kita-ku, Okayama 700-8530, Japan

Keywords:

Gloss Manipulation, Omnidirectional Lighting Environment, Specular Reﬂection, Polarization.

Abstract:

Manipulating the appearances of real-world objects by using active illumination is useful for XR. In this

paper, we propose a method for manipulating the gloss of real objects observed by our naked eyes under

omnidirectional lighting environments. Our proposed method makes use of the fact that specular reﬂection

components are sensitive to the polarization state of the incident light and the high-frequency components of

the illumination environment, while diffuse reﬂection components are insensitive to them. Speciﬁcally, our

method optimizes the polarization angles and intensities of incident lighting environments for manipulating

the gloss of real objects. We build a lighting system by using a dome screen and two pairs of a projector and a

transmissive LC panel for controlling both the polarization angles and high-frequency components of incident

lighting environments. We conduct a number of experiments, and show that our method achieves the gloss

manipulation without using the geometric and photometric properties of an object of interest.

1 INTRODUCTION

The appearance of an object depends not only on the

geometric and photometric properties of the object

but also on the light sources illuminating it. Manip-

ulating the appearances of real-world objects by us-

ing active illumination such as a projector and a light

stage is useful for XR (extended reality/cross reality).

In this paper, we focus on the gloss manipulation of

real objects under omnidirectional lighting environ-

ments.

A projector (or a projector-camera system) is use-

ful for manipulating the appearance of an object, in

particular for relighting and material editing (Raskar

et al., 2001; Siegl et al., 2015). This is because a

projector can pixel-wisely illuminate the object: it

can illuminate each point on the object surface with

different intensities and colors. Unfortunately, how-

ever, the appearance manipulation using a projector-

camera system requires the geometric and photomet-

ric properties of an object of interest or the light trans-

port of a scene.

On the other hand, a light stage is useful for re-

producing the appearance of an object under omnidi-

https://orcid.org/0000-0002-9819-3634

https://orcid.org/0000-0002-2183-7112

rectional lighting environments without using the ge-

ometric and photometric properties of the object (De-

bevec et al., 2002; Wenger et al., 2005; Debevec,

2012). Unfortunately, however, it is difﬁcult to ma-

nipulate the reﬂectance properties of the object, since

each light source illuminates the entire object. Ma et

al. (Ma et al., 2007) capture the specular-free images

under omnidirectional lighting environments by using

a light stage with ﬁxed linear polarizers and a camera

with a linear polarizer. However, the gloss manip-

ulation (emphasis and suppression) observed by our

naked eyes is still an open problem to be addressed.

In this paper, we propose a method for manipulat-

ing the gloss of real objects observed by our naked

eyes under omnidirectional lighting environments.

The key idea of our proposed method is the use of

polarized and high-frequency illumination. Speciﬁ-

cally, we make use of the fact that specular reﬂectance

is maximal/minimal when the polarization direction

is perpendicular/parallel to the outgoing plane, but

the diffuse reﬂectance is almost constant according to

the Fresnel equations (Shurcliff, 1962; Wolff, 1990).

In addition, we utilize the fact based on the fre-

quency analysis of reﬂection that specular/diffuse re-

ﬂection components are sensitive/insensitive to the

high-frequency components of an illumination distri-

bution (Ramamoorthi and Hanrahan, 2001b).

Miyoshi, Y., Kawahara, R. and Okabe, T.

Manipulating Gloss of Real Objects Under Omnidirectional Lighting.

DOI: 10.5220/0013386900003912

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 20th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2025) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 429-434

ISBN: 978-989-758-728-3; ISSN: 2184-4321

429

To control the intensity/color and polarization an-

gle of the incident light coming from each direction,

we build a programmable omnidirectional lighting

system by using a dome screen and two pairs of a

projector and a transmissive liquid crystal (LC) panel.

The projectors and the LC panels are used for con-

trolling the color/intensity and the polarization angle

respectively. Our proposed method manipulates the

gloss of real objects on the basis of the lookup table

constructed using a reference object with the same re-

fractive index as an object of interest without using

the geometric and photometric properties of the ob-

ject.

The main contributions of this study are threefold.

First, we propose a novel framework for manipulat-

ing the gloss of real objects observed by our naked

eyes under omnidirectional lighting environments on

the basis of the polarized and high-frequency illumi-

nation. Second, we build a novel lighting system by

using a dome screen and two pairs of a projector and

a transmissive LC panel for controlling both the po-

larization angles and high-frequency components of

incident lighting environments. Third, we achieve the

gloss manipulation without using the geometric and

photometric properties of an object of interest by us-

ing a reference object and a lookup table.

2 PROPOSED METHOD

2.1 Lighting System

Figure 1 shows our setup using two pairs of a projec-

tor and a transmissive LC panel

, a dome screen, and

a color camera. First, the light ray emitted from the

projector passes through the transmissive LC panel.

Second, it is reﬂected on the dome screen and inci-

dent to a target object. Third, it is reﬂected on the sur-

face of the target object, and ﬁnally the reﬂected light

is observed by the camera. We assume that the dome

screen is distant from the target object, and denote the

direction of the incident light seen from the object by

(θ,φ). Here, θ and φ are the zenith and azimuth an-

gles of the global spherical coordinate system whose

pole is the camera direction.

The projector controls the per-pixel intensity of

the light ray. The front linear polarizer of the trans-

missive LC panel is removed, and then it controls

the per-pixel angle of linear polarization. In addition,

the polarization-preserving material is painted on the

dome screen. Thus, our lighting system enables us to

We explain the reason why the two pairs are required

in Section 3.2.

Figure 1: Our setup using two pairs of a projector and a

transmissive LC panel, a dome screen, and a color camera.

control the intensity L(θ,φ) and the angle of linear po-

larization ω(θ,φ) of the light ray coming from (θ, φ)

to the target object.

2.2 Manipulation

Let us consider a mirror surface that reﬂects the light

ray coming from the direction (θ, φ) to the camera.

Since the light ray is reﬂected to the direction of the

mirror reﬂection, the surface normal is represented as

(θ/2,φ) by using the spherical coordinate system. In

other words, the incident angle to the mirror surface

is θ/2. We denote θ/2 by θ

′

hereafter.

It is known that the specular reﬂectance is max-

imal/minimal when the polarization direction is per-

pendicular/parallel to the outgoing plane spanned by

the surface normal and the direction of the reﬂected

light, i.e. the s-polarized light/p-polarized light (Shur-

cliff, 1962; Wolff, 1990). Therefore, the intensity of

the reﬂected light I(θ,φ) illuminated by unpolarized

light is described by

I(θ, φ) = L(θ, φ)

R(θ

′

). (1)

Here,

R(θ

′

) is the average of the maximal reﬂectance

(θ

′

) and the minimal reﬂectance R

(θ

′

R(θ

′

) =

(θ

′

) + R

(θ

′

)

. (2)

Our proposed method manipulates the gloss of

real object under omnidirectional lighting by control-

ling the intensity and the angle of linear polarization.

Speciﬁcally, we add the linear combination of spheri-

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

430

cal harmonics to the intensity as

′

(θ,φ) = L(θ, φ) +

∑

k=0

∑

m=−k

(θ,φ), (3)

where Y

(θ,φ) is the spherical harmonics of the k-

th degree and the m-th order and a

is its coefﬁcient

of the linear combination. We denote the reﬂectance

depending on the angle of linear polarization ω(θ,φ)

by R(θ

′

,ω(θ,φ)).

Therefore, the intensity of the reﬂected light

′

(θ,φ) after manipulation is described by

′

(θ,φ) = L

′

(θ,φ)R(θ

′

,ω(θ,φ))

L(θ,φ) +

∑

k=0

∑

m=−k

(θ,φ)

×R(θ

′

,ω(θ,φ)). (4)

Our proposed method controls the coefﬁcients of the

linear combination a

(k = 1,2,3,...,K,|m| ≤ k) and

the angle of linear polarization ω(θ,φ) so that the

gloss, i.e. specular reﬂection components observed

on the target object is emphasized or suppressed as

expected.

2.3 Optimization

We denote the target ratio, i.e. the desired ratio of the

emphasized/suppressed intensity and the original in-

tensity of gloss (specular reﬂection components) by t.

Our proposed method controls the coefﬁcients of the

linear combination a

and the angle of linear polar-

ization ω(θ,φ) so that

t ≃

′

(θ,φ)

I(θ, φ)

(5)

for all surface normals (θ

′

,φ) or equivalently for all

lighting directions (θ,φ).

In addition, our proposed method considers two

penalty terms. The ﬁrst one termed F

is the penalty

on negative lighting intensities:

(θ,φ) = max(−L

′

(θ,φ),0). (6)

The second one termed F

is the penalty on the change

in diffuse reﬂection components:

∑

k=0

∑

m=−k

k,m

|. (7)

Here, β

is the Fourier spectrum of the Lambertian

kernel; it represents the contribution of the Y

(θ,φ)

to the diffuse reﬂection components. It is known that

the ﬁrst nine low-frequency terms, i.e. k = 0,1,2 ex-

plain the power of 99.2% of diffuse reﬂection compo-

nents (Ramamoorthi and Hanrahan, 2001a).

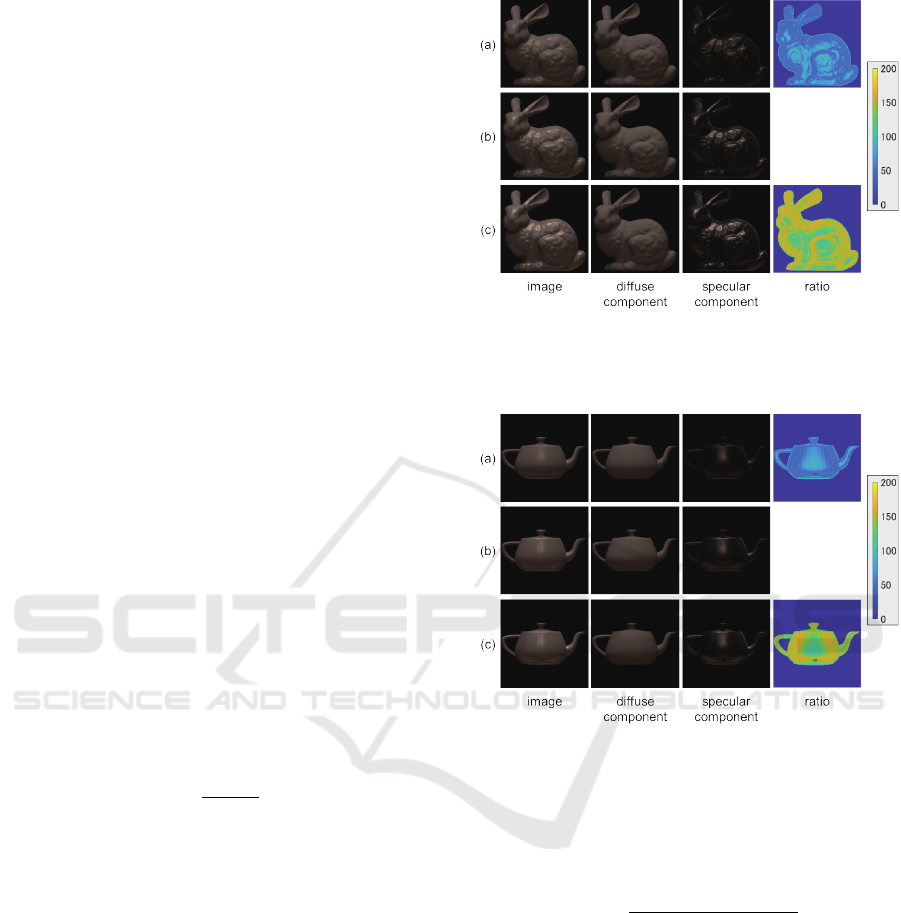
Figure 2: The results for the Stanford Bunny: (a) gloss

suppression (t = 0.5), (b) original, and (c) gloss emphasis

(t = 1.5) from top to bottom.

Figure 3: The results for the Utah Teapot: (a) gloss suppres-

sion (t = 0.5), (b) original, and (c) gloss emphasis (t = 1.5)

from top to bottom.

Thus, our proposed method results in the follow-

ing optimization:

min

a,ω

∑

θ,φ



′

(θ,φ)R(θ

′

,ω(θ,φ))

L(θ,φ)

R(θ

′

)

−t



+λ

∑

θ,φ

(θ,φ) + λ

. (8)

Here, a

a = (a

1−1

,···) and ω

ω is the set

of the polarization angles for each lighting direction

(θ,φ). We denote the weights of the second and third

terms by λ

and λ

respectively. We solve the above

minimization via alternative optimization; we itera-

tively ﬁx one of the a

a and ω

ω and optimize the other.

Note that our proposed method is applicable to

rough surfaces although the above derivation assumes

the mirror surface. This is because we can assume

that rough surfaces consist of the micro-facets of mir-

rors with various surface normals, and the ﬁrst term

Manipulating Gloss of Real Objects Under Omnidirectional Lighting

431

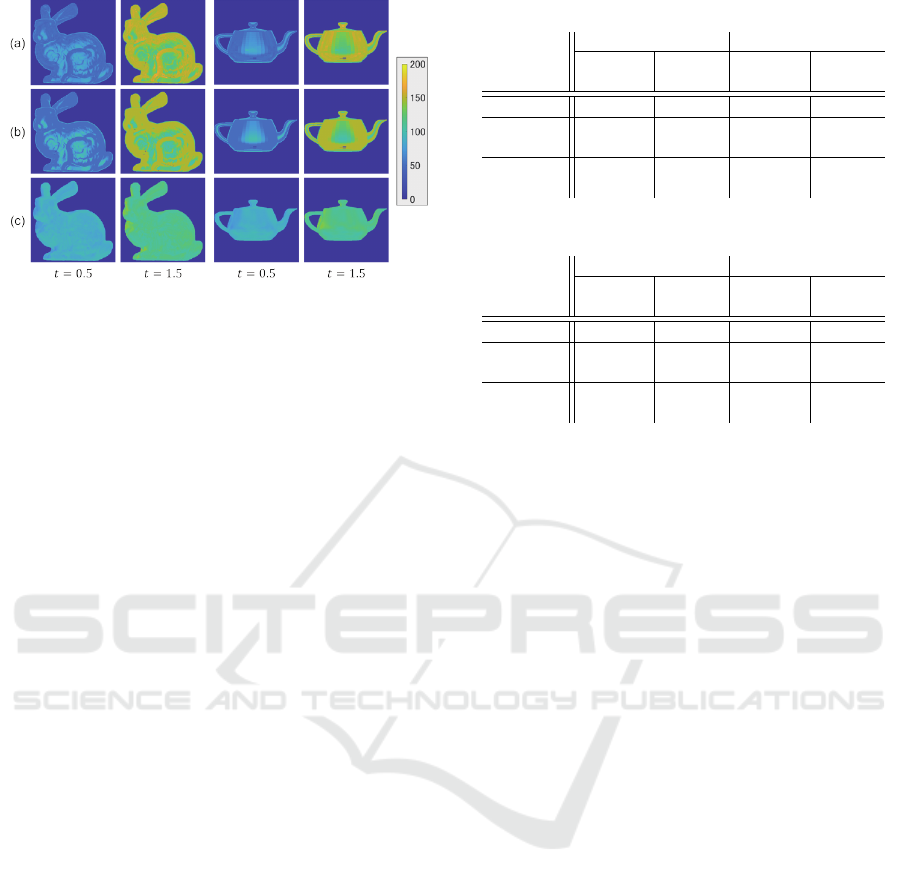
Figure 4: The ablation study for the Stanford Bunny (left)

and the Utah Teapot (right): (a) ours, (b) ours w/o high-

freq., and (c) ours w/o polarized from top to bottom.

in eq.(8) impose that the ratios for the all surface nor-

mals are close to the target ratio t.

3 EXPERIMENTS

3.1 Synthetic Images

First, we conducted the experiments using synthetic

images, for which the ground truth of diffuse and

specular reﬂection components are known, in order

to conﬁrm the effectiveness of our proposed method

both qualitatively and quantitatively.

Setup:

We used the Stanford Bunny and the Utah Teapot

for the target objects and the Grace Cathedral from

the light probe image gallery (Debevec, 1998) for the

lighting environment. We used Mitsuba 3 for ren-

dering images. We solved the minimization prob-

lem of eq.(8) by using the trust region reﬂective al-

gorithm (Coleman and Li, 1996) (MATLAB function

of lsqnonlin). We set the weights in eq.(8) as λ

= 10

and λ

= 5 × 10

respectively.

Results:

Figure 2 shows the results for the Stanford Bunny: the

output images, the diffuse reﬂection components, the

specular reﬂection components, and the ratios (%) of

the suppressed/emphasized specular reﬂection com-

ponents and the original ones from left to right. Com-

paring (a) gloss suppression (t = 0.5), (b) original,

and (c) gloss emphasis (t = 1.5), we can qualitatively

see that our proposed method suppresses/emphasizes

specular reﬂection components as expected while it

preserves diffuse reﬂection components. We can also

see that the accuracy of gloss manipulation is rela-

tively low for points with surface normals toward the

camera direction. This is because the degree of lin-

Table 1: The quantitative evaluation for the Stanford Bunny.

t = 0.5 t = 1.5

Specular Diffuse Specular Diffuse

(ratio) (SSIM) (ratio) (SSIM)

Ours 58.89% 0.99997 140.97% 0.99998

Ours w/o 61.50% 1.00000 137.79% 1.00000

high-freq.

Ours w/o 91.73% 0.99991 108.61% 0.99991

polarized

Table 2: The quantitative evaluation for the Utah Teapot.

t = 0.5 t = 1.5

Specular Diffuse Specular Diffuse

(ratio) (SSIM) (ratio) (SSIM)

Ours 59.42% 1.00000 138.93% 1.00000

Ours w/o 61.49% 1.00000 136.49% 1.00000

high-freq.

Ours w/o 91.31% 0.99997 108.08% 0.99997

polarized

ear polarization is low for those points, and the effect

of polarized incident light is somewhat limited. We

can see that we obtain the similar results for the Utah

Teapot as shown in Figure 3.

Figure 4 (left) and Table 1 shows the qualitative

and quantitative evaluation of our proposed method

for the Stanford Bunny. We can see that our method

works well; the ratios of the suppressed/emphasized

specular reﬂection components and the original ones

are almost the same as the target values: t = 0.5 (50%)

and t = 1.5 (150%). We can see that our method

works better than the use of only one of the polar-

ized illumination (Ours w/o high-freq.) and high-

frequency illumination (Ours w/o polarized). We can

see that we obtain the similar results for the Utah

Teapot as shown in Figure 4 (right) and Table2.

3.2 Real Images

Second, we conducted the experiments using real im-

ages, for which the ground truth of diffuse and spec-

ular reﬂection components are unknown, in order to

conﬁrm the effectiveness of our proposed method on

real images qualitatively.

Setup:

We used two pairs of a projector of MS524 from

BenQ and a transmissive LC panel, i.e. an LC panel

of JTP121LKNN from JNM Display without a front

polarization ﬁlter and a color camera of BFS-U3-

51S5PC-C from FLIR. We used two transmissive LC

panels because the range of the polarization angles of

each LC panel is at most 90

◦

as shown in Figure 5.

Then, we rotated one of the LC panel 90

◦

so that the

two LC panels covers the polarization angles from 0

◦

to 180

◦

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

432

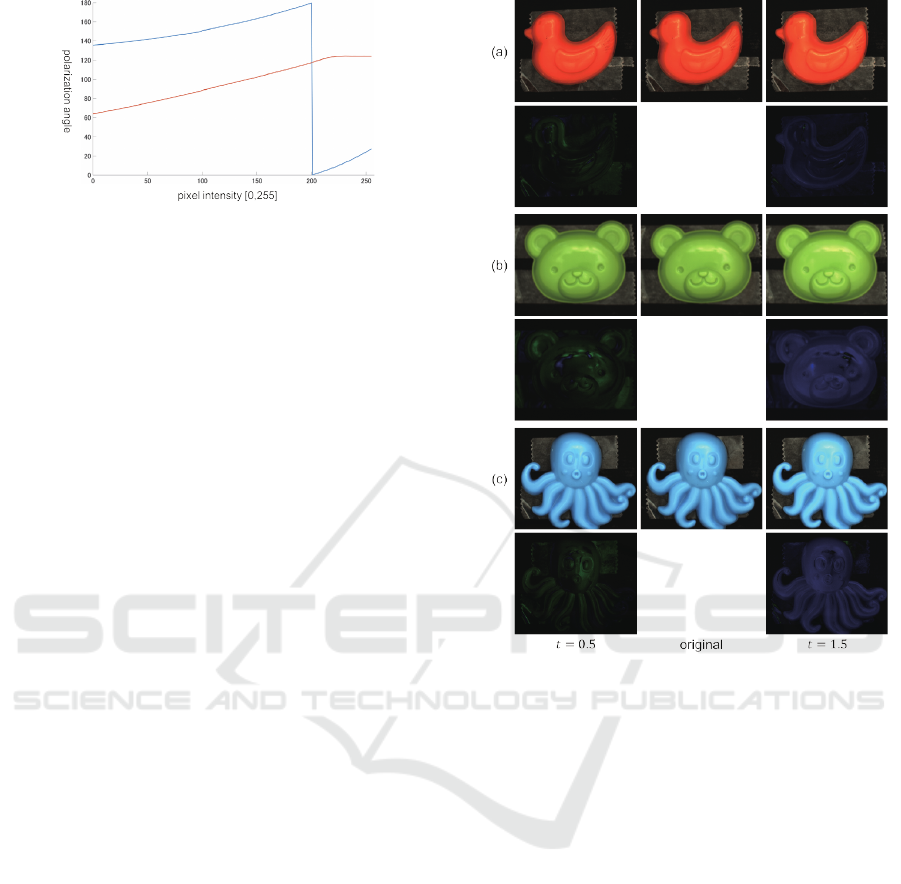
Figure 5: The polarization angles vs. the input pixel values

to the transmissive LC panels; the red and blue lines stand

for the polarization angle of the ﬁrst and the second LC pan-

els. Note that the second LC panel is rotated 90

◦

We conducted the geometric calibration of our

setup by using a mirror sphere. Speciﬁcally, we

estimated the correspondence between the projector

pixel, the LC panel pixel, and (θ,φ) by using struc-

tured light patterns.

We conducted the photometric calibration of our

setup by using a reference object with known shape;

we used a smooth specular sphere without diffuse re-

ﬂection components. Because the light rays incident

to an object surface from our lighting system is not

completely polarized but partially polarized, we made

the lookup table between the input pixel value to the

LC panel and R(θ

′

,ω(θ,φ)). Note that our proposed

method based on the above photometric calibration is

applicable to convex objects with the same refractive

index as the reference object.

In the same manner as the experiments using syn-

thetic images, we solved the minimization problem

of eq.(8) by using the trust region reﬂective algo-

rithm. We set the weights in eq.(8) as λ

= 10

and

= 5 × 10

respectively.

Results:

Figure 6 shows the results for the plastics toys: (a)

bird, (b) bear, and (c) octopus under the illumination

environment of the Grace Cathedral. The green and

blue images under the suppressed and emphasized

images show the difference images from the original

ones; we represent the positive/negative pixel values

as B/G channels. We multiply the pixel values of the

difference images by 5 for display purpose.

We can qualitatively see that our proposed method

suppresses/emphasizes specular reﬂection compo-

nents as expected. Note that we achieve such gloss

manipulation without using the geometric and photo-

metric properties of the target objects. We can also

see that some artifacts are slightly visible due to cast

shadows caused at concave areas.

Figure 6: The results using real images of the plastics toys:

(a) bird, (b) bear, and (c) octopus.

4 CONCLUSION

We proposed a novel framework for manipulating the

gloss of real objects observed by our naked eyes un-

der omnidirectional lighting environments on the ba-

sis of the polarized and high-frequency illumination.

In order to control both the polarization angles and

high-frequency components of incident lighting en-

vironments, we built a novel lighting system by us-

ing a dome screen and two pairs of a projector and

a transmissive LC panel. We conducted a number of

experiments using both synthetic and real images, and

conﬁrmed the effectiveness of our method.

One of the limitations of our proposed method is

the assumption of convex objects, i.e. no cast shad-

ows are observed on the objects’ surfaces. Another

limitation is the inter-reﬂection caused on the concave

screen. To cope with those limitations is the future

work of this study.

Manipulating Gloss of Real Objects Under Omnidirectional Lighting

433

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Numbers JP20H00612 and JP22K17914.

REFERENCES

Coleman, T. F. and Li, Y. (1996). An interior trust region ap-

proach for nonlinear minimization subject to bounds.

SIAM Journal on Optimization, 6(2):418–445.

Debevec, P. (1998). Rendering synthetic objects into real

scenes: bridging traditional and image-based graph-

ics with global illumination and high dynamic range

photography. In Proceedings of the 25th Annual Con-

ference on Computer Graphics and Interactive Tech-

niques, pages 189–198.

Debevec, P. (2012). The Light Stages and Their Applica-

tions to Photoreal Digital Actors. In In Proc. SIG-

GRAPH Asia2012, Technical Briefs.

Debevec, P., Wenger, A., Tchou, C., Gardner, A., Waese,

J., and Hawkins, T. (2002). A lighting reproduc-

tion approach to live-action compositing. ACM Trans.

Graph., pages 547–556.

Ma, W.-C., Hawkins, T., Peers, P., Chabert, C.-F., Weiss,

M., and Debevec, P. (2007). Rapid acquisition of spec-

ular and diffuse normal maps from polarized spheri-

cal gradient illumination. In Proceedings of the 18th

Eurographics Conference on Rendering Techniques,

pages 183–194.

Ramamoorthi, R. and Hanrahan, P. (2001a). On the rela-

tionship between radiance and irradiance: determin-

ing the illumination from images of a convex lamber-

tian object. J. Opt. Soc. Am. A, 18(10):2448–2459.

Ramamoorthi, R. and Hanrahan, P. (2001b). A signal-

processing framework for inverse rendering. In Pro-

ceedings of the 28th Annual Conference on Computer

Graphics and Interactive Techniques, page 117–128.

Raskar, R., Welch, G., Low, K.-L., and Bandyopadhyay, D.

(2001). Shader lamps: Animating real objects with

image-based illumination. In In Proc. EGSR2001,

pages 89–102.

Shurcliff, W. (1962). Polarized Light: Production and Use.

Harvard University Press.

Siegl, C., Colaianni, M., Thies, L., Thies, J., Zollh

ofer, M.,

Izadi, S., Stamminger, M., and Bauer, F. (2015). Real-

time pixel luminance optimization for dynamic multi-

projection mapping. ACM Trans. Graph., 34(6).

Wenger, A., Gardner, A., Tchou, C., Unger, J., Hawkins,

T., and Debevec, P. (2005). Performance relighting

and reﬂectance transformation with time-multiplexed

illumination. ACM Trans. Graph., 24(3):756–764.

Wolff, L. (1990). Polarization-based material classiﬁca-

tion from specular reﬂection. IEEE Trans. PAMI,

12(11):1059–1071.

GRAPP 2025 - 20th International Conference on Computer Graphics Theory and Applications

434