Making Reinforcement Learning Safer via Curriculum Learning

Kelvin Toonen and Thiago D. Sim

Department of Mathematics and Computer Science, Eindhoven University of Technology, The Netherlands

Keywords:

Safe Reinforcement Learning, Curriculum Learning, Constrained Reinforcement Learning.

Abstract:

The growth of deep reinforcement learning gives rise to safety concerns about applications using reinforcement

learning. Therefore, it is crucial to investigate the safety aspect in this ﬁeld, especially in the domain of robotics

where agents can break surrounding objects or themselves. Curriculum learning has the potential to help with

creating safer agents, because it helps the agent with learning faster and it allows for the agent to learn in safer

and more controlled environments leading up to the target environment. More speciﬁcally, we change the

environment only slightly to make it easier to transfer knowledge from one environment to the next, while still

inﬂuencing the exploration process of the agent. This project combines curriculum learning with constrained

reinforcement learning, a speciﬁc form of incorporating safety, to create a framework that allows agents to

learn safely, even during training. This framework is also extended to include automation of the curriculum.

1 INTRODUCTION

Deep reinforcement learning is quite prevalent in, for

example, the robotics domain and works by having

an agent, the model, learn how to behave in the en-

vironment by exploring and earning a reward when it

performs an action that we deem to be good. Here

we want to optimize the parameters of the agent in

such a way that the cumulative reward is maximized,

which is the objective of the agent. Ultimately, in

many practical applications, we want to do this with-

out having unwanted side effects or using unsafe ex-

ploration, which are more likely to occur in complex

agents and environments (Amodei et al., 2016).

Plenty of research has been done on safety in deep

reinforcement learning (Kadota et al., 2006; Sim

et al., 2021; Yang et al., 2023). Many of these meth-

ods still require a lot of training on top of the large

amount needed for regular reinforcement learning. As

this increases the number of environment interactions,

the agent has more opportunities to make mistakes.

For this research, we look at a method of creat-

ing safe agents in a faster way, namely through cur-

riculum learning. Curriculum learning is based on the

concept that, similar to humans, it is much easier for

an agent to learn a task by starting from easy exam-

ples and progressively making the task more difﬁcult

until the target task, the task that we want the agent to

perform, is reached (Narvekar et al., 2020).

Previous attempts at using curriculum learning for

safe reinforcement learning have focused on a strict

deﬁnition of safety, where a state is safe as long as the

agent can return to an initial state (Eysenbach et al.,

2018; Turchetta et al., 2020). This deﬁnition is lim-

iting as many more forms of unsafe scenarios exist,

where some small costs may be tolerated. An as-

pect that is often overlooked by similar discussions,

is that part, or the whole, of training is exempt from

considerations of safety. As in any real setting, mis-

takes during training are also very important, we want

to take the whole training process into account when

discussing safety. Furthermore, these approaches re-

quire the training of several additional agents to train

the primary agent.

For this research, we investigate the combination

of curriculum learning and safe reinforcement learn-

ing. We create a curriculum of tasks with slightly dif-

ferent environments that lead up to a target task where

we want to stay within certain safety constraints as

much as possible throughout training. The fact that

we create a curriculum through small changes in the

environment gives us the freedom to create safer ini-

tial environments to train on, while teaching the agent

valuable knowledge that it can use in the more un-

safe, safety-critical environments. This is ﬁrst done

for a static curriculum that is deﬁned before training

of any agents. Then this is extended to an adaptive

curriculum that adjusts based on the performance of

each individual agent. The creation of these curricula

does not require any pre-training or other agents to

Toonen, K. and Simão, T. D.

Making Reinforcement Learning Safer via Curriculum Learning.

DOI: 10.5220/0013388100003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 3, pages 1465-1472

ISBN: 978-989-758-737-5; ISSN: 2184-433X

1465

help train the primary agent, giving it an edge in this

regard to state of the art.

Contribution. We propose a framework using cur-

riculum learning that reduces the safety regret of RL

agents with minimal loss in task performance. The

sequencing for this curriculum is adaptive, meaning

that it allows the agents to go to more difﬁcult tasks

only when they are considered ready.

2 RELATED WORK

Constrained RL. In safe RL there are two common

approaches to incorporating safety: ones that alter

the optimization criterion (Basu et al., 2008; Tamar

et al., 2013), or ones that alter the exploration process

(Tang et al., 2010; Sim

ao et al., 2021; Yang et al.,

2023). Constrained RL falls into the former category

and has sprung forth many different ways of incorpo-

rating safety through constraints. Many approaches

exist that use Lagrangian relaxation to include the

constraints in the objective directly (Ray et al., 2019;

Zhang et al., 2020; Yang et al., 2022) or use a simi-

lar approach through penalty functions (Zhang et al.,

2022). Others use trust regions together with approx-

imations of the objective and constraints (Achiam

et al., 2017), or stop the episode when the agent has

exceeded the cost limit (Sun et al., 2021).

Curriculum Learning in RL. Curriculum learning

is much harder to categorize in a similar way, due

to the vast amount of techniques used. Search algo-

rithms are used to ﬁnd a good ordering of the tasks by

training agents on different curricula (Foglino et al.,

2019a; Foglino et al., 2019b). In a similar fash-

ion, a curriculum can be created iteratively by start-

ing on the target task and then creating prior tasks

that teach the agent what it was unable to do in the

current task (Narvekar et al., 2016). GANs can be

used to create a generator that generates the tasks and

a discriminator that decides whether they are of ap-

propriate difﬁculty (Florensa et al., 2018). Self-paced

learning uses a distribution over possible tasks and ad-

justs the distribution based on the performance of the

agent, moving to more difﬁcult tasks when the agent

does well (Klink et al., 2019; Klink et al., 2021; Eimer

et al., 2021).

Curriculum Learning in Safe RL. There is not

much research that combines curriculum learning in

safe RL. One of these few performs curriculum induc-

tion by training two agents, one that learns the task

and another that “resets” the former agent by mov-

ing it back to an initial state (Eysenbach et al., 2018).

The algorithm induces a curriculum for the resetting

agent only, as the better both agents become, the later

the early abort will occur. Therefore, it learns to re-

cover from more distant states as both agents learn.

A similar research extends this concept by replacing

the resetting agent with a teacher, who has access to a

collection of resetting agents and learns when to use

which of them (Turchetta et al., 2020). To do this, the

teacher must be trained on several students such that

it can adaptively choose the next resetting agent for

any student. A major limitation of these approaches

is their deﬁnition of safety. They deﬁne any unrecov-

erable state as unsafe, which is a very restricting deﬁ-

nition. Therefore, we want to use a more general def-

inition of safety, namely that of satisfying some con-

straints. This is an extension of their deﬁnition, as

we can add the constraint that we cannot go into any

unrecoverable states.

3 BACKGROUND

This section introduces constrained RL and curricu-

lum learning. Finally, it formalizes the problem of

designing a curriculum to improve the safety of con-

strained RL.

3.1 Constrained RL

Constrained RL is a form of safe RL where safety

is deﬁned as staying within certain constraints,

such as requiring the expected return to be high

enough (Kadota et al., 2006). Adding such constraints

to a Markov decision process (MDP) results in a con-

strained MDP that describes the process with those

constraints (Altman, 1999). The goal of constrained

RL is to train the agent to stay within these con-

straints. This is often done by penalizing the viola-

tion of the constraints (Smith et al., 1997; Altman,

1998). In this paper, we will focus on the constraint

that limits the costs that the agent is allowed to incur.

Note that costs in this context are different from nega-

tive rewards, as they have semantics that cannot easily

be translated to rewards, such as energy consumption.

Intuitively, they represent actions that the agent can

only execute a limited number of times.

Deﬁnition 3.1 (Constrained MDP). We deﬁne a con-

strained MDP as the tuple ⟨S; A; p;r; c;α⟩ with S the

state space, A the action space, p : S × A × S → [0, 1]

the transition function, r : S × A × S → R the reward

function, c : S ×A×S → R the cost function and α the

cost limit.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

1466

Figure 1: The target task from our experiments. Red is the

agent, green is the goal, blue are the hazards and yellow

are the possible starting locations, where a higher opacity

relates to a higher probability of starting there.

An example environment can be found in Fig-

ure 1, where the agent needs to reach the goal. How-

ever, going over the hazards results in costs, as it, for

example, may be a difﬁcult-to-traverse area that re-

sults in a lot of energy consumption. Therefore a con-

straint on these costs would allow the agent to reach

the goal without running out of energy.

Similarly to the return that is deﬁned as the cu-

mulative discounted reward R =

∑

∞

t=0

, where t is

the time step, r

represents the reward, and γ ∈ [0,1]

is the discount factor that allows the inﬂuence of fu-

ture rewards to be controlled (Puterman, 1994), we

deﬁne the notion of cumulative discounted cost C =

∑

∞

t=0

, where c

is the cost at time step t. To op-

timize, the agents need an objective and in this case,

the constrained criterion is:

max

π∈Π

(R) subject to E

While there are multiple ways to constrain the cost,

we choose to bound the expected cumulative cost be-

cause it is the simplest and most widely used (Wachi

et al., 2024). Similarly to the return, this is ap-

proximated through the cost value function V

(C | s

= s),, which is the expected cumulative

discounted cost following policy π starting from the

starting states s

3.2 Curriculum Learning

The idea of curriculum learning is that it is easier to

learn a complex task by iteratively building up to that

task than to start on that task immediately. A curricu-

lum is a sequence of tasks, which in this context are

constrained MDPs, such that the order accelerates or

improves learning. Curriculum learning is then ﬁnd-

ing a curriculum such that the order of tasks is opti-

mized (Narvekar et al., 2020).

Curriculum learning has three main elements:

task generation, task sequencing, and transfer learn-

ing (Narvekar et al., 2020). Here we focus on task

sequencing, where we allow only changes in the re-

ward, cost and transition functions, and in the starting

or goal state distributions between different tasks in

the curriculum.

Deﬁnition 3.2 (Curriculum). A curriculum is deﬁned

as a directed acyclic graph ⟨V ,E , T ,g⟩, where V

is the set of vertices, E is the set of directed edges

{(v

i+1

) | (v

i+1

) ∈ V × V }, T is the set of tasks

= ⟨S; A; p

;α⟩, where a task is thus a con-

strained MDP, and g : V → T is a function that as-

sociates each vertex with a task.

In the case of a linear curriculum, before we can

train on the task of node v

i+1

, we need to train on the

task of node v

. There also is a single sink node v

that

contains the target task.

Many different types of curriculum learning tech-

niques exist, but we put an emphasis on their different

levels of automation. We distinguish between four

levels of automation that each build upon the previ-

ous level. The ﬁrst level is a fully hand-made cur-

riculum, where the tasks are created and ordered by

hand. The second level is automated task sequencing,

where the order of tasks is calculated beforehand by

an algorithm and where these tasks are still created by

humans. The third level is adaptive task sequencing,

where it is adaptively decided for each agent individ-

ually when a task change should occur during training

through an algorithm. Finally, the fourth level is au-

tomated task generation, where also the creation of

tasks is automated such that each element of the cur-

riculum generation is automated.

4 PROBLEM STATEMENT

Our goal is to ﬁnd whether curriculum learning al-

lows for safer learning for the agents. To measure

safety within a constrained MDP, we use an adapted

deﬁnition of constraint violation regret from (Efroni

et al., 2020). This is useful as it ignores the cost if it

is below the allowed limit, which means that this met-

ric works better than simply taking the total cost in-

curred (M

uller et al., 2024). The constraint violation

regret, which we will shorten to regret, is deﬁned as:

Reg(K, c, α) =

∑

k=1

) − α]

, (2)

where K is the number of episodes, π

is the policy at

episode k, s

is the starting state and [x]

= max(x, 0).

We use regret to compare performance with respect to

safety, as it does not sufﬁce to look at the difference in

constraint violation. This is the case as in constrained

RL it does not matter how much the constraint is vi-

olated, only whether it is violated. Furthermore, we

put an emphasis on the safety during training, thus

we need a metric that can summarize the performance

over several episodes.

Making Reinforcement Learning Safer via Curriculum Learning

1467

(a) Task 0 (b) Task 1 (c) Task 2

(d) Task 3 (e) Task 4 (f) Task 5

Figure 2: Curriculum tasks used for most experiments. Red is the agent, green is the goal, blue are the hazards and yellow are

the possible starting locations, where a higher opacity relates to a higher probability of starting there.

Using the deﬁnitions from the previous sections,

the goal of our research is the following. We want

to build a curriculum ⟨V ,E, T , g⟩ that helps an agent

solve constrained MDP m

∈ T according to Crite-

rion 1, associated with vertex v

, while minimizing

the regret Reg(K,c

,α) at each vertex.

5 CURRICULUM LEARNING

FOR CONSTRAINED RL

We describe the methods that we use to create an

automated curriculum learning algorithm for con-

strained RL.

5.1 Hand-Made Curriculum

As a ﬁrst step a hand-made curriculum is created,

which will be expanded to contain some automation.

To create a curriculum ⟨V ,E,T , g⟩, we follow four

guidelines (Peng et al., 2018). We isolate complexity

by creating tasks that try to teach the agent one new

skill, such as not going in a straight line to the goal if

there is a hazard in the way. This is done by select-

ing the simplest environments to introduce one com-

plexity at a time, meaning that we create the simplest

versions of the tasks that teach the agent a new skill.

These tasks are chosen such that they are most simi-

lar to the target environment, such as by introducing

more and more parts of the target environment into

the tasks. This is also an example of introducing com-

plexity by building on previous tasks, which in general

can be done by requiring skills learned from previous

tasks to complete the current task. In this way, a cur-

riculum can be created with an implied ordering.

The resulting tasks can be found in Figure 2,

where each task is slightly more difﬁcult than the

tasks before. These tasks all share the same state

space S and action space A, so it therefore falls in

our deﬁnition of only having small changes between

the tasks. Now the set of tasks T is clear, we need

to create g to map vertices V to each of these tasks.

This is simple as we can just map the ith vertex to the

ith task:

g(v

) = m

,∀i ∈ [0,6], (3)

where v

∈ V , m

∈ T and |V | = |T | = 7. The only

remaining part of the curriculum is E , which deter-

mines the relationship between tasks. As we have

created a curriculum with a linear ordering, we will

create the edges as:

= (v

i+1

),∀i ∈ [0,5], (4)

with e

∈ E and |E| = 6.

Schedule. Although we have deﬁned a curriculum,

in practice we still need to deﬁne when to change

tasks. There are too many options to try all of them,

but we will follow some general heuristics. The ﬁrst

one is that later tasks, which are also the harder tasks

as they require the knowledge of previous ones, need

progressively more training time. The second is that

we do not want to train until convergence for each

intermediate task, because there might be a risk of

overﬁtting on an easy task, resulting in possibly un-

safe behavior in future tasks. More importantly, it

is faster to not train until convergence (Narvekar and

Stone, 2019). As for this type of curriculum, it needs

to be decided beforehand when the task changes oc-

cur, we need to look at when the average agent con-

verges and stop the task some episodes before that.

After some small experiments, we decided to change

tasks at epochs 10, 20, 40, 100, 300 and 700, where

there is thus a shift from task 0 to 1 at epoch 10, from

task 1 to 2 at epoch 20, etc. In our case, an epoch is

1000 steps and may consist of multiple episodes.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

1468

Algorithm 1: Learning algorithm with an adaptive curricu-

lum for the basic instantiation.

Input: Number of training epochs n

Input: Task distribution ⃗p

Input: Cost constraint α

Input: Cost threshold factor β

Input: Threshold of successful epochs needed κ

1: k ← 0 ▷ The number of successful epochs

2: for i = 0, 1, ..., n do

3: Sample task m

∼ ⃗p

4: task completed, cost ← Train on task m

5: if task completed and cost ≤ β · α then

6: k ← k + 1

7: if k ≥ κ then

8: UPDATEDISTRIBUTION(⃗p

) ▷ This shifts the

Dirac distribution to the next task

9: k ← 0 ▷ Reset counter of successful epochs

5.2 Adaptive Curriculum

To automate part of the curriculum, we make the se-

quencing adaptive, which means that each curricu-

lum is tailored to the speciﬁc agent in terms of task

changes. For our approach, we take inspiration from

two other approaches by generalizing them and com-

bining them. One of these strategies maintains a prob-

ability distribution over the tasks and shifts the dis-

tribution to harder tasks on a successful episode or to

easier tasks on an unsuccessful episode (Wu and Tian,

2017). The other strategy allows the agent to move on

to the next task in the sequence only when the change

in Q-values between updates is small enough, indicat-

ing that the agent has converged on this task (Asada

et al., 1996). These two methods can be combined

by using a probability distribution over the tasks and

ﬁnding a good measure to decide when and how the

distribution over the tasks should shift.

In this research, we take a very basic approach that

uses a Dirac distribution ⃗p

over the tasks and where

we only allow the distribution to shift to the next task

or stay at the current task. Furthermore, we introduce

hyperparameters κ and β, where κ is the amount of

epochs where the agents needs to have completed an

episode with an expected cost of at most β · α. Here β

is based on the idea that we can either be lenient with

the cost limit, larger than 1, to allow for reaching the

target task quicker or that we can be strict with the

cost limit, smaller than 1, forcing the agent to already

be very safe on the intermediate tasks. The expected

cost is used instead of the actual cost, as this is what

the agent is optimizing for and we want to decrease

the inﬂuence of lucky starting positions, by not using

the exact costs made during the epochs.

Pseudocode for this algorithm can be found in Al-

gorithm 1. At the start of each epoch, we sample a

task from the distribution ⃗p

(Line 3), which can be

any distribution, but in this case it is a Dirac distri-

bution with probability 1 on task 0. After training on

this task (Line 4), we look at the cost and whether

an episode has been completed, and check if this re-

sulted in a successful epoch (Lines 5-6). The condi-

tion in the if-statement can be changed depending on

the deﬁnition of a successful episode. After this if-

statement, we check whether there were enough suc-

cessful epochs on this distribution (Line 7). If this is

the case we update the distribution to be a Dirac dis-

tribution over the next task and reset the number of

successful epochs (Line 8). The condition in the if-

statement and the exact functionality of updating the

distribution can be changed depending on the strategy

for when to change the distribution.

6 EMPIRICAL EVALUATION

We ﬁrst set up experiments for the static hand-made

curriculum and then for the adaptive curriculum.

For the experiments, we train agents using sev-

eral different safe RL algorithms with a cost limit of

5, which has as a consequence that the agent can-

not go through the center of a hazard or through the

overlapping area of two adjacent hazards without go-

ing over this limit. For most algorithms, we train

a baseline version without using the curriculum and

a curriculum version, and later adaptive curriculum

version, trained with their respective curricula. The

only exceptions are PPO (Schulman et al., 2017) and

CPO (Achiam et al., 2017), which are trained with

only a baseline version. Here PPO is a general RL

algorithm that gives us insights mainly about the opti-

mal return when not considering constraints and CPO

is a very popular safe RL algorithm that we con-

sider less promising for use with a curriculum than

the other algorithms.

Although our experiments primarily focus on

safety during training, we also evaluate the agents on

the target task throughout training, for 5 episodes ev-

ery 10 epochs.

6.1 Static Curriculum

Comparing Safe RL Algorithms. The agents used

in this experiment consist of a curriculum version

and a baseline version, which does not use a cur-

riculum, of the algorithms CRPO (Xu et al., 2021),

CUP (Yang et al., 2022), FOCOPS (Zhang et al.,

2020), PCPO (Yang et al., 2020), PPOEarlyTermi-

nated (Sun et al., 2021) and PPOLag (Ray et al.,

2019). For PPOLag we have performed some hyper-

Making Reinforcement Learning Safer via Curriculum Learning

1469

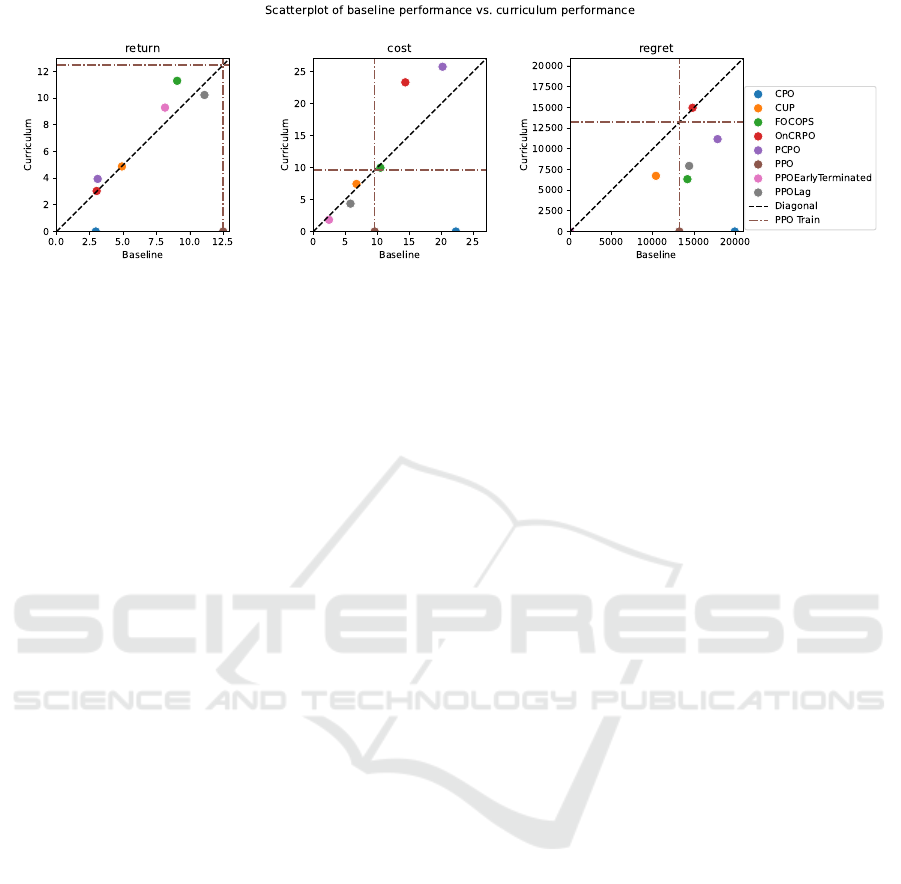
Figure 3: Plots showing how the algorithms performed with and without the curriculum, with the target task being task 4.

The return and cost are the average of the metric in the ﬁnal epoch of each repetition and the regret is the average of each

repetition. Since PPO and CPO have only been used for the baseline, their respective curriculum values are considered 0.

parameter tuning to ﬁnd proper Lagrangian param-

eters for agents without a curriculum, which were

also used for the curriculum version. We included

two more agents with only a baseline version, namely

PPO and CPO. The agents are trained with task 4 as

the target task, as the goal of this experiment is to ﬁnd

if there are safe RL algorithms that beneﬁt more from

using a curriculum. Since task 4 is a relatively easy

target task, we expect the agents to converge and thus

give proper insights into what a curriculum changes in

terms of their performance. Both types of agents are

trained for 1000 epochs, which means that the cur-

riculum agent trains for 900 epochs on task 4.

Figure 3 shows the results during training of the

experiments. Most agents trained with a curriculum

have a lower regret compared to the baselines, while

the return is about as good. Most of the agents trained

with a curriculum also end up with a lower regret than

the PPO agent, while for the baseline agents only the

CUP and PPOEarlyTerminated versions manage to do

so. The end costs are comparable between the two

versions, but there are two cases where the curriculum

version has a higher cost. However, these costs are ex-

treme for both versions, as an expected cost of 15 is

already three times the cost limit. With all of these

insights, the best-performing algorithms are PPOLag,

FOCOPS, CUP and PPOEarlyTerminated. These four

are used for the other experiments. Note that PPOEar-

lyTerminated cannot have a cost above the cost limit,

as the episode ends when the agent would go above

the limit.

6.2 Adaptive Curriculum

Comparing to Baseline and Static Curriculum.

The agents used in this experiment consist of an adap-

tive curriculum version, a static curriculum version

and a baseline version, which does not use a curricu-

lum, of the algorithms CUP, FOCOPS, PPOLag and

PPOEarlyTerminated. We included two more agents

with only a baseline version, namely PPO and CPO.

The agents are trained on each task in the curriculum

as the target task, except for task 0, resulting in six

subexperiments that each have a different task as a

target task. This means that ﬁrst task 1 is used as the

target task, where the baseline versions train only on

task 1, while both curriculum versions consider the

whole curriculum to only contain tasks 0 and 1, i.e.

the curriculum up to and including this target task.

Then similarly for task 2 and all tasks up to and in-

cluding the actual target task. This is done to inves-

tigate the difference in performance of the three ver-

sions with different levels of difﬁculty for the target

task and different lengths of the curriculum.

Figure 4 shows the results of these experiments

for the PPOLag agent on the last three tasks. The

adaptive curriculum version has a lower regret than

the other two versions on all tasks. This is due to

the decrease in the initial cost spike that the baseline

experiences and, to a lesser extent, the static curricu-

lum. The return is slightly lower for both curriculum

versions, compared to the baseline. However, the suc-

cess rate, which indicates the percentage of evaluation

episodes that reached the goal with a cost below the

cost limit, shows that the versions are much closer.

Adaptive Curriculum Task Progression. Due to

the implementation of the adaptive curriculum, the

agent is not guaranteed to reach the target task, as

it may never consider itself ready to do so. Figure 5

shows the task progression of individual agents per al-

gorithm, where it can be seen that most of the PPOLag

and PPOEarlyTerminated agents did eventually reach

the target task, but for CUP and FOCOPS agents this

was not the case. Regardless, patterns can be seen in

the task progression where there are many agents that

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

1470

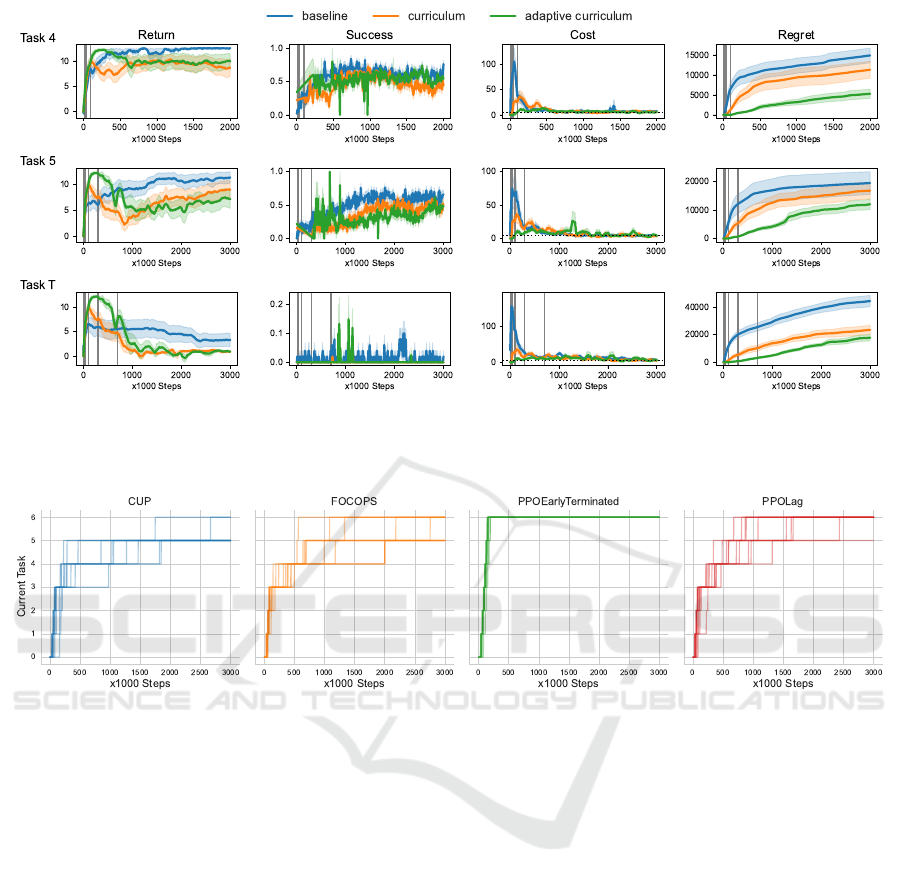
Figure 4: Training performance curves of the PPOLag agents, comparing baseline, curriculum and adaptive curriculum

progression. The shaded area indicates the standard error. The vertical grey lines indicate the epochs at which a task change

occurs for the curriculum agents. The horizontal dashed line in the cost plots represents the cost limit.

Figure 5: Task progression of the different safe RL algorithms used with an adaptive curriculum.

switch to the next task at roughly the same time. This

means that it is possible to use such results to create

a better static curriculum, which can guarantee that

agents reach the target task.

7 CONCLUSIONS

In this work, we investigated the impact of a curricu-

lum on the safety regret of a safe RL agent. We pro-

posed an adaptive curriculum that asserts the compe-

tency of each agent and allows them to move on to

more difﬁcult tasks in the curriculum when they have

shown to be safe enough on the current task.

Through empirical evaluation, we concluded that

using a static curriculum reduces safety regret during

training, with minimal performance loss. Our version

of an adaptive curriculum improved on our static cur-

riculum in the same way. This is due to the reduction

in the cost spike near the start of training, which is a

consequence of ﬁrst training the agents on easier tasks

to understand the basics of the environment.

Future Work. Our approach requires tasks to be

designed beforehand. Therefore, a logical next step

would be to automate task generation. However, it

is not clear how to automatically design new tasks

where the agent will remain safe. Furthermore, the

tasks that we created are focused on changing the

position of hazards. Therefore, investigating curric-

ula that change the starting positions or the cost limit

throughout training could lead to new insights.

REFERENCES

Achiam, J., Held, D., Tamar, A., and Abbeel, P. (2017).

Constrained policy optimization. In ICML, pages 22–

31. PMLR.

Altman, E. (1998). Constrained Markov decision pro-

cesses with total cost criteria: Lagrangian approach

and dual linear program. Math. Methods Oper. Res.,

48(3):387–417.

Making Reinforcement Learning Safer via Curriculum Learning

1471

Altman, E. (1999). Constrained Markov Decision Pro-

cesses, volume 7. Routledge.

Amodei, D., Olah, C., Steinhardt, J., Christiano, P. F.,

Schulman, J., and Man

e, D. (2016). Concrete prob-

lems in AI safety. CoRR, abs/1606.06565.

Asada, M., Noda, S., Tawaratsumida, S., and Hosoda, K.

(1996). Purposive behavior acquisition for a real

robot by vision-based reinforcement learning. Mach.

Learn., 23(2-3):279–303.

Basu, A., Bhattacharyya, T., and Borkar, V. S. (2008). A

learning algorithm for risk-sensitive cost. Math. Oper.

Res., 33(4):880–898.

Efroni, Y., Mannor, S., and Pirotta, M. (2020). Exploration-

exploitation in constrained MDPs. arXiv preprint

arXiv:2003.02189.

Eimer, T., Biedenkapp, A., Hutter, F., and Lindauer, M.

(2021). Self-paced context evaluation for contextual

reinforcement learning. In ICML, pages 2948–2958.

PMLR.

Eysenbach, B., Gu, S., Ibarz, J., and Levine, S. (2018).

Leave no trace: Learning to reset for safe and au-

tonomous reinforcement learning. In ICLR (Poster).

OpenReview.net.

Florensa, C., Held, D., Geng, X., and Abbeel, P. (2018).

Automatic goal generation for reinforcement learning

agents. In ICML, pages 1514–1523. PMLR.

Foglino, F., Christakou, C. C., and Leonetti, M. (2019a). An

optimization framework for task sequencing in cur-

riculum learning. In ICDL-EPIROB, pages 207–214.

IEEE.

Foglino, F., Leonetti, M., Sagratella, S., and Seccia, R.

(2019b). A gray-box approach for curriculum learn-

ing. In WCGO, pages 720–729. Springer.

Kadota, Y., Kurano, M., and Yasuda, M. (2006). Dis-

counted Markov decision processes with utility con-

straints. Comput. Math. Appl., 51(2):279–284.

Klink, P., Abdulsamad, H., Belousov, B., D’Eramo, C.,

Peters, J., and Pajarinen, J. (2021). A probabilis-

tic interpretation of self-paced learning with applica-

tions to reinforcement learning. J. Mach. Learn. Res.,

22:182:1–182:52.

Klink, P., Abdulsamad, H., Belousov, B., and Peters, J.

(2019). Self-paced contextual reinforcement learning.

In CoRL, pages 513–529. PMLR.

uller, A., Alatur, P., Cevher, V., Ramponi, G., and He, N.

(2024). Truly no-regret learning in constrained MDPs.

In ICML. OpenReview.net.

Narvekar, S., Peng, B., Leonetti, M., Sinapov, J., Taylor,

M. E., and Stone, P. (2020). Curriculum learning for

reinforcement learning domains: A framework and

survey. J. Mach. Learn. Res., 21:181:1–181:50.

Narvekar, S., Sinapov, J., Leonetti, M., and Stone, P. (2016).

Source task creation for curriculum learning. In AA-

MAS, pages 566–574. ACM.

Narvekar, S. and Stone, P. (2019). Learning curricu-

lum policies for reinforcement learning. In AA-

MAS, pages 25–33. International Foundation for Au-

tonomous Agents and Multiagent Systems.

Peng, B., MacGlashan, J., Loftin, R. T., Littman, M. L.,

Roberts, D. L., and Taylor, M. E. (2018). Curricu-

lum design for machine learners in sequential deci-

sion tasks. IEEE Trans. Emerg. Top. Comput. Intell.,

2(4):268–277.

Puterman, M. L. (1994). Markov Decision Processes: Dis-

crete Stochastic Dynamic Programming. Wiley Series

in Probability and Statistics. Wiley.

Ray, A., Achiam, J., and Amodei, D. (2019). Benchmarking

safe exploration in deep reinforcement learning.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. CoRR, abs/1707.06347.

Sim

ao, T. D., Jansen, N., and Spaan, M. T. J. (2021). Al-

wayssafe: Reinforcement learning without safety con-

straint violations during training. In AAMAS, pages

1226–1235. ACM.

Smith, A. E., Coit, D. W., Baeck, T., Fogel, D., and

Michalewicz, Z. (1997). Penalty functions. Handbook

of evolutionary computation, 97(1).

Sun, H., Xu, Z., Fang, M., Peng, Z., Guo, J., Dai, B., and

Zhou, B. (2021). Safe exploration by solving early

terminated MDP. CoRR, abs/2107.04200.

Tamar, A., Xu, H., and Mannor, S. (2013). Scaling

up robust mdps by reinforcement learning. CoRR,

abs/1306.6189.

Tang, J., Singh, A., Goehausen, N., and Abbeel, P. (2010).

Parameterized maneuver learning for autonomous he-

licopter ﬂight. In ICRA, pages 1142–1148. IEEE.

Turchetta, M., Kolobov, A., Shah, S., Krause, A., and Agar-

wal, A. (2020). Safe reinforcement learning via cur-

riculum induction. In NeurIPS.

Wachi, A., Shen, X., and Sui, Y. (2024). A survey of con-

straint formulations in safe reinforcement learning. In

IJCAI, pages 8262–8271. ijcai.org.

Wu, Y. and Tian, Y. (2017). Training agent for ﬁrst-person

shooter game with actor-critic curriculum learning. In

ICLR (Poster). OpenReview.net.

Xu, T., Liang, Y., and Lan, G. (2021). CRPO: A new

approach for safe reinforcement learning with con-

vergence guarantee. In ICML, pages 11480–11491.

PMLR.

Yang, L., Ji, J., Dai, J., Zhang, L., Zhou, B., Li, P., Yang,

Y., and Pan, G. (2022). Constrained update projection

approach to safe policy optimization. In NeurIPS.

Yang, Q., Sim

ao, T. D., Jansen, N., Tindemans, S. H., and

Spaan, M. T. J. (2023). Reinforcement learning by

guided safe exploration. In ECAI, pages 2858–2865.

IOS Press.

Yang, T., Rosca, J., Narasimhan, K., and Ramadge, P. J.

(2020). Projection-based constrained policy optimiza-

tion. In ICLR. OpenReview.net.

Zhang, L., Shen, L., Yang, L., Chen, S., Wang, X., Yuan,

B., and Tao, D. (2022). Penalized proximal policy op-

timization for safe reinforcement learning. In IJCAI,

pages 3744–3750. ijcai.org.

Zhang, Y., Vuong, Q., and Ross, K. W. (2020). First order

constrained optimization in policy space. In NeurIPS.

ICAART 2025 - 17th International Conference on Agents and Artiﬁcial Intelligence

1472