Reducing QUBO Density by Factoring out Semi-Symmetries

Jonas N

ußlein

, Leo S

unkel

, Jonas Stein

, Tobias Rohe

, Dani

elle Schuman

, Sebastian Feld

Corey O’Meara

, Giorgio Cortiana

and Claudia Linnhoff-Popien

Institute of Computer Science, LMU Munich, Germany

Quantum & Computer Engineering Department, Delft University of Technology, The Netherlands

E.ON Digital Technology GmbH, Germany

Keywords:

QAOA, Quantum Annealing, QUBO, Couplings, Symmetry, Ising, Circuit Depth.

Abstract:

Quantum Approximate Optimization Algorithm (QAOA) and Quantum Annealing are prominent approaches

for solving combinatorial optimization problems, such as those formulated as Quadratic Unconstrained Binary

Optimization (QUBO). These algorithms aim to minimize the objective function x

Qx, where Q is a QUBO

matrix. However, the number of two-qubit CNOT gates in QAOA circuits and the complexity of problem

embeddings in Quantum Annealing scale linearly with the number of non-zero couplings in Q, contributing

to signiﬁcant computational and error-related challenges. To address this, we introduce the concept of semi-

symmetries in QUBO matrices and propose an algorithm for identifying and factoring these symmetries into

ancilla qubits. Semi-symmetries frequently arise in optimization problems such as Maximum Clique, Hamilton

Cycles, Graph Coloring, and Graph Isomorphism. We theoretically demonstrate that the modiﬁed QUBO ma-

trix Q

mod

retains the same energy spectrum as the original Q. Experimental evaluations on the aforementioned

problems show that our algorithm reduces the number of couplings and QAOA circuit depth by up to 45%.

For Quantum Annealing, these reductions also lead to sparser problem embeddings, shorter qubit chains and

better performance. This work highlights the utility of exploiting QUBO matrix structure to optimize quantum

algorithms, advancing their scalability and practical applicability to real-world combinatorial problems.

1 INTRODUCTION

The Quantum Approximate Optimization Algorithm

(QAOA) (Farhi et al., 2014) is designed to tackle com-

binatorial optimization problems using quantum com-

puters by preparing a quantum state that maximizes

the expectation value of the cost-hamiltonian. QAOA

is widely recognized as a prime contender for show-

casing quantum advantage on Noisy Intermediate-

Scale Quantum (NISQ) devices (Zou, 2023). It aims

to approximate the ground state of a given physical

system, often referred to as the Hamiltonian. How-

ever, its successful implementation faces challenges

due to the high error rates inherent in current near-

term quantum devices, which lack full error correc-

tion capabilities.

Utilizing QAOA to solve a problem entails a two-

step process. Initially, the problem is translated into

a parametric quantum circuit consisting of p layers

each consisting of 2 adjustable parameters, where p

is a hyperparameter that needs to be set manually.

This circuit is then run for thousands of trials. Subse-

quently, a classical optimizer utilizes the expectation

value of the output distribution to reﬁne the parame-

ters. This iterative process continues until the optimal

parameters for the circuit are determined. The cost

function, which QAOA tries to minimize is usually

represented as a Quadratic Unconstrained Binary Op-

timization (QUBO) problem.

The quantity of two-qubit CNOT operations

within a QAOA circuit is equal to 2C · p where C

is the number of non-zero couplings in the QUBO

(number of edges in the problem graph). However,

CNOT operations are susceptible to errors and of-

ten lead to prolonged runtimes. For instance, on

the Google Sycamore quantum processor (Ayanzadeh

et al., 2023), CNOTs exhibit an average error-rate

of 1%. Furthermore, CNOT gates might require ad-

ditional SWAP gates since control- and target-qubit

might not be connected on the hardware chip. There-

fore, minimizing the number of these operations be-

comes crucial to improve the efﬁciency and accuracy

of quantum optimization algorithms like QAOA.

In this paper, we therefore propose a method for

using ancilla qubits to reduce the number of non-zero

couplings and therefore also the number of CNOT op-

Nüßlein, J., Sünkel, L., Stein, J., Rohe, T., Schuman, D., Feld, S., O’Meara, C., Cortiana, G. and Linnhoff-Popien, C.

Reducing QUBO Density by Factoring out Semi-Symmetries.

DOI: 10.5220/0013395900003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 1, pages 783-792

ISBN: 978-989-758-737-5; ISSN: 2184-433X

783

erations and the depth of the QAOA circuit. We will

also show that these sparser (but larger) QUBO matri-

ces are easier to solve using Quantum Annealing since

lower density leads to shorter physical qubit chains.

We present the concept of semi-symmetries (see

Deﬁnition 2) which we factor out into ancilla qubits.

Our algorithm can therefore create different QUBO

matrices that represent the same low-energy spec-

trum. To demonstrate the effectiveness of our ap-

proach, we tested it on four well-known optimiza-

tion problems: Maximum Clique, Hamilton Cycles,

Graph Coloring, and Graph Isomorphism. Our results

show that our method can reduce the number of cou-

plings and QAOA circuit depth by up to 45%, thus

signiﬁcantly improving the efﬁciency and scalability

of Quantum Annealing and QAOA for solving a di-

verse range of NP-hard optimization problems.

2 BACKGROUND

2.1 Quadratic Unconstrained Binary

Optimization

Let Q be a symmetric, real-valued (n × n)-matrix

and x ∈ B

be a binary vector. Quadratic Uncon-

strained Binary Optimization (QUBO) (Zielinski

et al., 2023b; Roch et al., 2023) is an optimization

problem of the form:

∗

= argmin

H(x) = argmin

∑

i=1

∑

j=i

i j

(1)

The function H(x) is usually called Hamiltonian.

We will refer to the matrix Q as the “QUBO ma-

trix”. The task is to ﬁnd a binary vector x that is as

close as possible to the optimum which is known to

be NP-hard (Glover et al., 2018). QUBOs attracted

special attention recently since they can be solved

using Quantum Optimization approaches like Quan-

tum Annealing (QA) (Morita and Nishimori, 2008) or

QAOA (Farhi et al., 2014) which promises speed-ups

compared to classical algorithms (Farhi and Harrow,

2016). Numerous problems have already be encoded

as a QUBO formulation (Bucher et al., 2023; Zielin-

ski et al., 2023a; N

ußlein et al., 2023).

To solve a QUBO matrix using Quantum Anneal-

ing (QA), it must ﬁrst be embedded onto a specialized

graph (Prasanna et al., 2019; Mooney et al., 2019;

Lodewijks, 2020). This process involves represent-

ing each logical qubit with multiple physical qubits.

These physical qubits must be interconnected, form-

ing what is known as a chain.

2.2 QAOA

The Quantum Approximate Optimization Algorithm

(QAOA) is a hybrid quantum-classical algorithm pro-

posed by Farhi et al. in 2014 (Farhi et al., 2014)

for solving combinatorial optimization problems. Let

C(x) be a cost function, where x represents a binary

string encoding a possible solution. The goal is to

ﬁnd the x that minimizes C(x). QAOA encodes this

optimization problem into a quantum circuit, which

can be parameterized by angles γ and β. The quantum

circuit prepares a quantum state |ψ(γ,β)⟩ that repre-

sents a superposition of all possible solutions. The

quantum circuit consists of alternating layers of two

types of operators: the cost operator U

and the mixer

operator U

. The cost operator is responsible for en-

coding the cost function into the quantum state, while

the mixer operator is responsible for exploring differ-

ent solutions efﬁciently. The quantum state |ψ(γ,β)⟩

prepared by the circuit is given by:

|ψ(γ,β)⟩ = e

−iγ

−iβ

···e

−iγ

−iβ

|+⟩

⊗n

where |+⟩

⊗n

represents the initial state of n qubits ini-

tialized to the superposition state, and U

and U

are

the cost and mixer operators, respectively which are

applied p times. p is a hyperparameter that needs to

be manually speciﬁed. The parameters γ and β control

the evolution of the quantum state.

The next step involves optimizing the parameters

γ and β to minimize the expectation value of the cost

function. This optimization process is typically per-

formed using classical optimization algorithms such

as gradient descent or genetic algorithms. Given

the quantum state |ψ(γ,β)⟩, the expectation value

of the cost function can be calculated as E(γ,β) =

⟨ψ(γ,β)|C|ψ(γ, β)⟩. The goal is to ﬁnd the optimal

parameters γ

∗

and β

∗

that minimize E(γ, β). This opti-

mization process involves iteratively updating the pa-

rameters.

2.3 Maximum Clique

In graph theory, the Maximum Clique problem

involves ﬁnding the largest subset of vertices V

′

⊆ V

in a graph G(V,E) such that every pair of vertices is

connected by an edge. This problem has extensive

applications across various domains, including social

network analysis and bioinformatics (Eblen et al.,

2011; Rossi et al., 2015). To formulate the Maximum

Clique problem as a QUBO problem, binary variables

are used for each vertex i, where x

= 1 indicates

that vertex i is included in the clique, and x

= 0

otherwise. The Hamiltonian can therefore be written

as:

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

784

H(x) =

∑

−x

+ A ·

∑

(i, j)∈E

The second summand of H enforces the solution

to be a clique while the ﬁrst summand rewards larger

cliques (Lucas, 2014).

2.4 Hamilton Cycles

Let G(V,E) be a graph. The Hamilton Cycles prob-

lem asks if there is a path that starts from vertex v

visits every other vertice exactly once, and ends in

vertex v

(Lucas, 2014). This problem has practi-

cal applications in various ﬁelds, including logistics,

transportation, and circuit design (Kawarabayashi,

2001; Laporte and Mart

ın, 2007). To formulate this

problem as a QUBO we introduce binary variables x

i, j

with i ∈ [1..|V |] and j ∈ [1..|V |]. x

i, j

= 1 iff vertex i is

at position j of the cycle. The Hamiltonian can now

be written as (N

ußlein et al., 2022):

H(x) =

∑

−x

+ A ·

∑

i, j

∑

k,l

i, j

k,l

· I[i = k ∨ j = l

∨ (l = j + 1 ∧ (i,k) /∈ E) ∨ (l = |V | − 1 ∧ j = 0

∧ (i,k) /∈ E)]

H consists of three constraints: (1) each vertex

must be visited (2) two vertices can’t be at the same

position in the cycle (3) two vertices can not be in

neighboring positions of the cycle if there is no edge

in the graph connecting them.

2.5 Graph Coloring

The Graph Coloring problem encompasses a wide

range of applications from scheduling to register

allocation in compilers, and even to radio fre-

quency assignment in wireless communication net-

works (Ahmed, 2012). At its core, the problem re-

volves around assigning colors to the vertices of a

graph in such a way that no two adjacent vertices

share the same color. Let G = (V,E) be a graph, and

k be the number of available colors. To formulate this

problem as a QUBO we introduce binary variables x

i,k

representing the assignment of color k to vertex i (Lu-

cas, 2014).

H(x) =

∑

i,k

−x

i,k

+ A ·

∑

i,k

∑

j,k

i,k

j,k

· I[i = j

∨ (k

= k

∧ (i, j) ∈ E)]

H encodes the two constraints that each vertex can

only have one color and two adjacent vertices can’t

have the same color.

2.6 Graph Isomorphism

Graph Isomorphism (GI) is an important problem in

graph theory that asks whether two graphs are struc-

turally equivalent, albeit possibly differing in their

vertex and edge labels. Formally, two graphs G

) and G

= (V

) are considered isomor-

phic if there exists a bijective mapping between their

vertices such that their edge structures remain un-

changed. In contrast to Maximum Clique, Hamilton

Cycles and Graph Coloring, the complexity class for

GI is still unknown (although it is expected to be in

NP-intermediate) (Lu, ).

To formulate GI as a QUBO problem, we intro-

duce binary variables x

i, j

representing the mapping of

vertex i of G

to vertex j of G

. The Hamiltonian can

now be formulated as (Lucas, 2014):

H(x) =

∑

−x

+ A ·

∑

, j

∑

, j

I[i

= j

∨ j

= j

∨ ((i

) ∈ E

∧ ( j

, j

) /∈ E

)

∨ ((i

) /∈ E

∧ ( j

, j

) ∈ E

)]

3 RELATED WORK

In this paper, we propose the concept of Semi-

Symmetries in QUBO matrices Q and an algorithm

for factoring them out into ancilla qubits to reduce

the number of couplings and therefore the number of

CNOT gates and circuit depth in QAOA and the chain

length in QA. There are already two well-known

types of symmetries in QUBO matrices: bit-ﬂip-

symmetry and qubit-permutation-symmetry (Shay-

dulin and Galda, 2021; Shaydulin and Wild, 2021;

Shaydulin et al., 2020). Symmetry is deﬁned here re-

garding the solution vectors {x} and their associated

energies {x

Qx}.

3.1 Bit-Flip-Symmetry

Bit-ﬂip-symmetry denotes the property of QUBOs that

the inverse bit vector x

= 1 − x to a bit vector x both

have the same energy: (x

)

= x

Qx. Bit-ﬂip-

symmetries occur, for example, in the Max-Cut prob-

lem:

H(x) =

∑

(i, j)∈E

−x

− x

+ 2x

Bit-ﬂip-symmetry can be identiﬁed in a QUBO matrix

Reducing QUBO Density by Factoring out Semi-Symmetries

785

Q by substituting x

← (1 − x

) and x

← (1 − x

H(x) =

∑

(i, j)∈E

−(1 − x

) − (1 − x

) + 2(1 − x

)(1 − x

) =

∑

(i, j)∈E

−2 + x

+ x

+ 2(1 −x

− x

+ x

) =

∑

(i, j)∈E

−x

− x

+ 2x

Since the energy stays the same the QUBO contains a

bit-ﬂip-symmetry. Eliminating bit-ﬂip-symmetry can

be done by removing the last qubit and assigning it the

value 0. Then, the remaining (n −1) × (n −1) QUBO

matrix still encodes the original Hamiltonian.

3.2 Qubit-Permutation-Symmetry

Qubits i and j are qubit-permutation-symmetrical if

they have the same coupling values to all other qubits,

i.e.:

∀ k ∈ [1..n] : Q

i,k

= Q

j,k

This implies that for all x

(i=1, j=0)

it holds:

H(x

(i=1, j=0)

) = H(x

(i=0, j=1)

)

We use the notation x

(i=1, j=0)

for an arbitrary solution

vector x with qubit i having value 1 and qubit j having

value 0. However, a trivial reduction of such a QUBO

is not possible, since there are 3 cases that have dif-

ferent energies: x

(i=0, j=0)

, x

(i=1, j=0)

and x

(i=1, j=1)

3.3 Choosing a Value for P

Several works (Niu et al., 2019; Pan et al., 2022b;

Ni et al., 2023) have analyzed the inﬂuence of circuit

depth on the performance of QAOA. Note that depth

is sometimes used synonymously with the number of

layers, which we refer to as p. In this paper, we ex-

clusively refer to depth as the depth of the transpiled

quantum circuit. To select the optimal number of rep-

etitions p, several approaches have been proposed for

automatically setting this hyperparameter (Pan et al.,

2022b; Ni et al., 2023; Pan et al., 2022a; Lee et al.,

2021). In our experiments, we always used p = 1.

3.4 Other Approaches for Eliminating

Couplings in Q

In Algorithm 1, the original Q is modiﬁed by factor-

ing out semi-symmetries into additional ancilla qubits.

However, we show that in doing so, the energy land-

scape for valid solutions is not altered. In contrast,

there are heuristic approaches that alter the energy

landscape to simplify Q. For example, in the paper

(Sax et al., 2020), an approach was introduced to re-

duce the number of couplings in a QUBO by simply

setting the smallest couplings to 0 since they have the

smallest inﬂuence on the energy landscape. By al-

tering the energy landscape in this manner, it can no

longer be guaranteed that the optimal solution x

∗

mod

the modiﬁed QUBO Q

mod

corresponds to the optimal

solution x

∗

of the original QUBO Q.

Ising graphs associated to real-world problems,

such as Airport Trafﬁc Graphs, often exhibit a power-

law structure (Ayanzadeh et al., 2023), where some

nodes have many more connections than others. In

the paper (Ayanzadeh et al., 2023), an approach is pre-

sented on how to partition the graphs with respect to

these ’hubs’. This eliminates many couplings of the

Hamiltonian, and the individual subgraphs can then

be solved individually using a divide-and-conquer ap-

proach. A detailed analysis of the performance of

QAOA depending on the graph structure is provided

in (Herrman et al., 2021). In (Ponce et al., 2023),

an approach is proposed on how large Max-Cut QU-

BOs can be solved by decomposing them into many

smaller QUBOs. A similar approach is pursued in

(Majumdar et al., 2021).

There are already several papers (Shaydulin and

Galda, 2021; Shaydulin and Wild, 2021; Shaydulin

et al., 2020) that exploit symmetries in QUBOs

to generate more efﬁcient and shorter QAOA cir-

cuits. In (Shaydulin and Galda, 2021), a method is

proposed for leveraging bit-ﬂip-symmetry and qubit-

permutation-symmetry on Max-Cut graphs. In (Shay-

dulin et al., 2020) various types of symmetries that are

relevant to QAOA and classical optimization prob-

lems are discussed. One prominent type is variable

(qubit) permutation symmetries, which are transfor-

mations that rearrange the qubits of the quantum state

without changing the problem’s objective function.

Such a symmetry can be caused when a graph con-

tains automorphisms (a mapping of the graph to it-

self). The authors show that if a group of variable per-

mutations leaves the objective function invariant, then

the output probabilities of QAOA will be the same

across all bit strings connected by such permutations,

regardless of the chosen QAOA parameters and depth

which can be used to reduce the dimension of the ef-

fective Hilbert space.

4 ALGORITHM

We start this section by providing a formal deﬁnition

of conﬂicting qubits and semi-symmetries.

Deﬁnition 1 (Conﬂicting qubits). Let H(x) = x

be the energy of a solution x. Qubits i and j are

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

786

called conﬂicting, iff for every solution x

(i=1, j=1)

holds that:

H(x

(i=1, j=1)

) > {H(x

(i=1, j=0)

),H(x

(i=0, j=1)

),H(x

(i=0, j=0)

)}

Deﬁnition 2 (Semi-symmetry). Conﬂicting qubits

(i, j) are semi-symmetric if and only if:

∃U ⊆ {1..n}\{i, j}∧|U| ≥ 3 : ∀k ∈ U : Q

i,k

= Q

j,k

̸= 0

In other words, two conﬂicting qubits (i, j) are semi-

symmetric iff there are at least 3 other qubits to which

i and j have the same non-zero couplings. This is a

weakened deﬁnition of symmetry compared to qubit-

permutation-symmetry where qubits i and j needed

the same couplings to all other qubits.

4.1 Proof-of-Concept Example

In the following section, we demonstrate our algo-

rithm for a simple proof-of-concept example. To do

this, we consider the following graph:

Figure 1: A simple proof-of-concept graph.

We now want to ﬁnd the largest clique (Maximum

Clique) for the graph G = (V, E) in Figure 1, i.e. the

largest set of nodes for which each pair of nodes is

connected by an edge. The Hamiltonian that encodes

this problem is given by :

H =

∑

−x

∑

(i, j)∈E

The QUBO matrix Q for Maximum Clique and the

graph from Figure 1 is listed in Table I (upper). It

requires 6 qubits and 9 couplings. Q contains a semi-

symmetry between qubits 2 and 5 which can be fac-

tored out into an additional ancilla qubit 7 (see Table

I (lower)). The modiﬁed QUBO matrix Q

mod

requires

7 qubits but only 8 couplings.

In the following section, we theoretically show

that our algorithm doesn’t change the energy land-

scape for valid solutions and in section 4.3 we analyze

the energy spectra for both QUBO matrices in Table

Algorithm 1: Factoring Semi-Symmetries.

Input: QUBO matrix Q of size n × n

number of ancillas numAncillas ∈ N

parameter z ∈ R

new

= n

cL = GETCONFLICTLIST(Q,n

new

)

while len(cL) > 0 do

syms,(i, j) = GETMOSTSYMQUBITS(Q,n

new

,cL)

if len(syms) < 3 or n

new

= n + numAncillas then

break

end if

new

= n

new

+ 1

Q = ENHANCE(Q,n

new

,(i, j), syms)

cL = GETCONFLICTLIST(Q,n

new

)

end while

return Q

function GETCONFLICTLIST(Q,n)

cL = []

Z = [

∑

j∈[1..n],Q

i, j

: i ∈ [1..n]]

for i = 1 to n, j = 1 to n do

if i < j and Q

i, j

> −Z[i] − Z[ j] then

cL.append((i, j))

end if

end for

return cL

end function

function GETMOSTSYMQUBITS(Q,n,cL)

best = (0, 1)

bestSyms = []

for (i, j) ∈ cL do

syms = [k ∈ [1..n] : Q

i,k

= Q

j,k

̸= 0]

if len(syms) ≥ len(bestSyms) then

best = (i, j)

bestSyms = syms

end if

end for

return bestSyms,best

end function

function ENHANCE(Q, n,(i, j),syms)

i,i

= Q

i,i

+ z

j, j

= Q

j, j

+ z

n,n

= z

i,n

= −2 · z

j,n

= −2 · z

i, j

= 2 · z

for k ∈ syms do

k,n

= Q

i,k

= 0

j,k

= 0

end for

return Q

end function

Reducing QUBO Density by Factoring out Semi-Symmetries

787

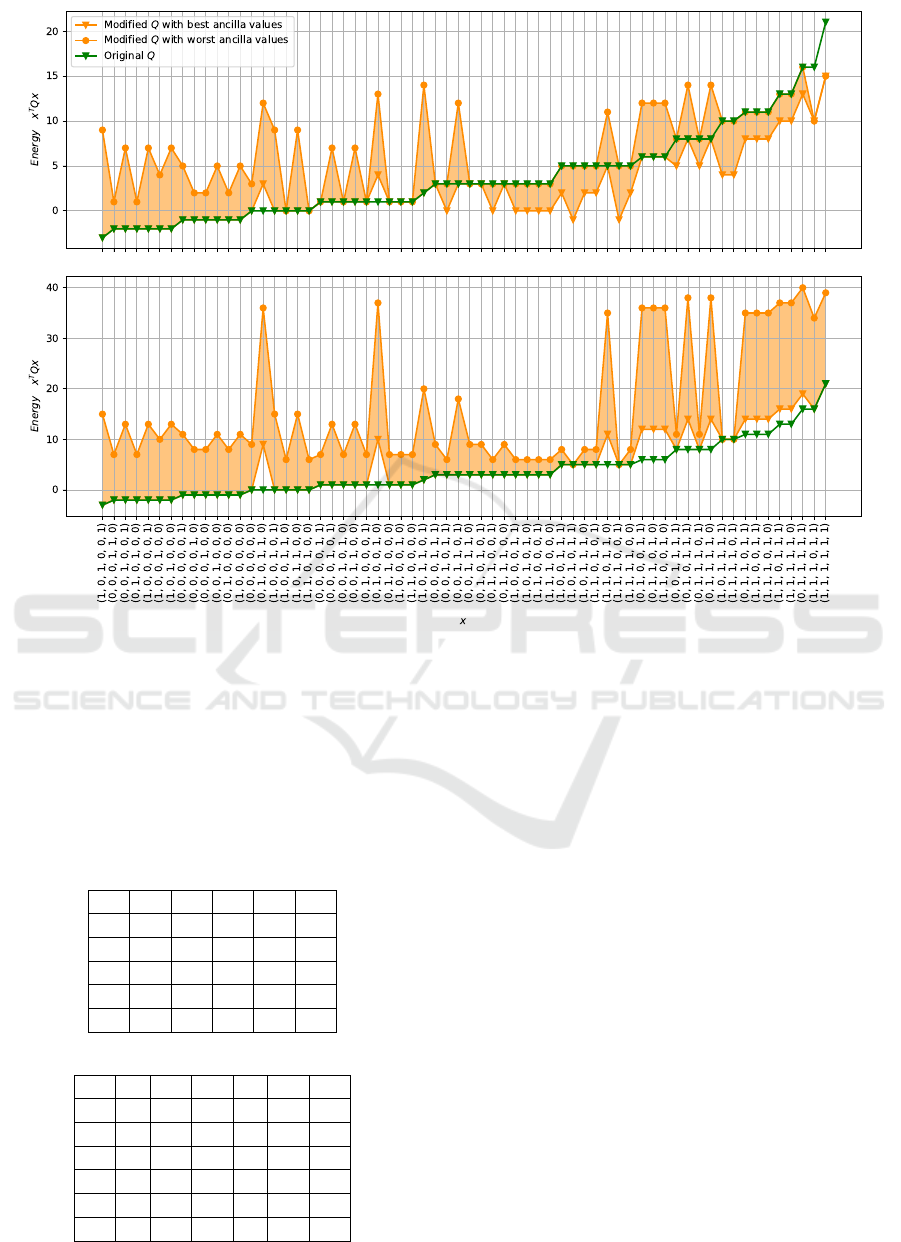
Figure 2: The green line represents the sorted energy spectrum of the left QUBO in Table I. The orange lines represent the

energy spectrum of the right QUBO in Table I with the lower graph in both plots being the energetically more favorable choice

of the ancilla value while the upper graph in both plots representing the energetically less favorable choice. The upper plot

represents the energy spectrum of Q

mod

with z = 3 and the lower plot with z = 9. For z = 3 we can see that invalid solutions

can have a lower energy in Q

mod

than in Q but if we increase z all invalid solutions have an energy equal or higher than in Q.

But even z = 3 is already sufﬁcient for the global optimum x

∗

in Q to also be the global optimum in Q

mod

Table 1: (Upper) QUBO matrix Q for Maximum Clique

and the graph in Figure 1. (Lower) Modiﬁed QUBO ma-

trix Q

mod

of Q using Algorithm 1. The semi-symmetry be-

tween qubits 2 and 5 was factored out into an additional

ancilla qubit.

-1 3 3

-1 3 3 3

-1 3 3

-1 3

-1

-1 3

2 9 -6

-1 3 3

-1 3

2 -6

-1 3

4.2 Theoretical Analysis for Correctness

We can prove that our modiﬁed QUBO Q

mod

has the

same optimal solutions as Q with the best choice of

ancilla values, i.e. Algorithm 1 doesn’t change the

energies of valid solutions and doesn’t decrease the

energy of invalid solutions. Valid solutions x are bit-

vectors that don’t violate conﬂicting qubit constraints,

i.e. if (i, j) are conﬂicting then x

= 0 or x

= 0. In-

valid solutions are bit-vectors with x

= 1 and x

= 1.

Proposition 1. If we choose z =

∑

(i, j)

i, j

|, valid

solutions x have the same energy regarding Q as

to Q

mod

with the best values for the ancilla qubits

mod

= x +[x

]. The energy of invalid solution doesn’t

decrease with respect to Q

mod

even with the best an-

cilla values.

Proof. Let Q be any QUBO matrix and x ∈ B

be any

solution vector. The energy E for x corresponds to

E = x

Qx. Let (x

) be a pair of conﬂicting qubits,

i.e. no valid solution x contains assignments i = 1 and

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

788

j = 1 at the same time. Further assume that (x

)

are semi-symmetrical and Algorithm 1 factored out

the semi-symmetries into an ancilla qubit x

Case 1: x

= 0, x

= 0: in this case, we can

easily see that the energy of x

mod

= x + [0] regard-

ing Q

mod

is identical to the original energy: E

mod

(x + [0])

· Q

mod

· (x + [0]) = E.

Case 2: x

= 0,x

= 1: in this case the

modiﬁed energy corresponds to: E

mod

= E + z +

∑

k∈syms

i,k

. Since we can choose z =

∑

(i, j)

i, j

|, it

holds that z +

∑

k∈syms

i,k

≥ 0. Therefore: E

mod

≥ E.

Case 3: x

= 1, x

= 0, x

= 0: E

mod

= E + z −

∑

k∈syms

i,k

. Again, since z =

∑

(i, j)

i, j

|, it holds that

z −

∑

k∈syms

i,k

≥ 0. Therefore: E

mod

≥ E.

Case 4: x

= 1,x

= 0,x

= 1: E

mod

= E +z+z −2z+

∑

k∈syms

i,k

−

∑

k∈syms

i,k

= E.

Case 5: x

= 0,x

= 1,x

= 0: analogous to case 3.

Case 6: x

= 0,x

= 1,x

= 0: analogous to case 4.

Case 7: x

= 1,x

= 0: E

mod

= E +z+z +2z−

∑

k∈syms

i,k

−

∑

k∈syms

i,k

> E.

Case 8: x

= 1, x

= 1: E

mod

= E + z +

z + z − 2z − 2z + 2z −

∑

k∈syms

i,k

−

∑

k∈syms

i,k

∑

k∈syms

i,k

= E + z −

∑

k∈syms

i,k

≥ E.

The best choices for the ancilla qubit for valid solu-

tions are case 1, case 4 and case 6 which all have

energy E. Therefore, the energy did not change for

valid solutions. For invalid solutions (cases 7 and 8)

the energy does not decrease.

4.3 Empirical Evaluation of the Energy

Landscape for the PoC

We now empirically investigate this theoretical ﬁnd-

ing in our proof-of-concept example. Since there are

6 qubits, there are 2

= 64 possible solutions x. For

each x we calculated the energy regarding Q (Table

I, left), see green lines in Figure 2. Further, we have

calculated the energy in the modiﬁed QUBO (Table

I, right) with both possible values (0 and 1) for the

ancilla qubit 7. Then we have plotted for each x the

original energy, the energy in the modiﬁed Q

mod

with

the worse choice for the ancilla qubit and the better

choice for the ancilla qubit.

The upper plot in Figure 2 shows the result with

z = 3, and the lower plot shows the result with z =

9. We can verify the proposition if we choose z

big enough, but often a lower value for z is already

enough for the original optimal solution x to also be

the optimal solution in Q

mod

5 EXPERIMENTS

We conducted experiments on four representative

combinatorial optimization problems — Maximum

Clique, Graph Coloring, Hamilton Cycles, and Graph

Isomorphism — to evaluate the impact of removing

semi-symmetries from QUBO formulations. Each

problem instance is characterized by the number of

vertices |V | and edges |E|, with additional parameters

such as the number of colors k for Graph Coloring.

Our goal was to assess how introducing additional an-

cilla qubits (to remove semi-symmetries) inﬂuences

key hardware-related metrics after embedding the re-

sulting QUBOs onto a quantum annealer.

Figure 3 summarizes our ﬁndings. The ﬁgure con-

sists of a 4 × 5 grid of plots, where each row corre-

sponds to one of the four problems (from top to bot-

tom: Maximum Clique, Graph Coloring, Hamilton

Cycles, Graph Isomorphism) and each column rep-

resents a different metric. The metrics we considered

were: the number of couplers used in the embedded

QUBO, the total number of physical qubits, the mean

chain length, the chain break fraction, and the prob-

ability of a successful solution (Success). The hor-

izontal axis in every subplot denotes the number of

vertices |V | for the given problem instances, thus cap-

turing how problem scale affects these metrics. We

compared three scenarios for each problem and set-

ting: the original QUBO (blue), and two symmetry-

free variants obtained by introducing 5 (orange) or 10

(green) ancilla qubits to remove semi-symmetries.

As the problem size |V | increased, the original

QUBO instances tended to produce larger and more

complex embeddings, reﬂected by a higher number

of couplers, more physical qubits, and longer chains.

These embedding characteristics often led to a higher

chain break fraction and, consequently, a lower prob-

ability of success. In contrast, when we introduced

ancilla qubits to remove semi-symmetries, both the 5-

and 10-ancilla conﬁgurations showed a noticeable re-

duction in complexity: we observed fewer couplers, a

smaller chain length, and a reduced chain break frac-

tion. This improved embedding quality often trans-

lated into a higher success probability for ﬁnding the

optimal solution, despite the growing complexity of

the underlying problem instances.

Reducing QUBO Density by Factoring out Semi-Symmetries

789

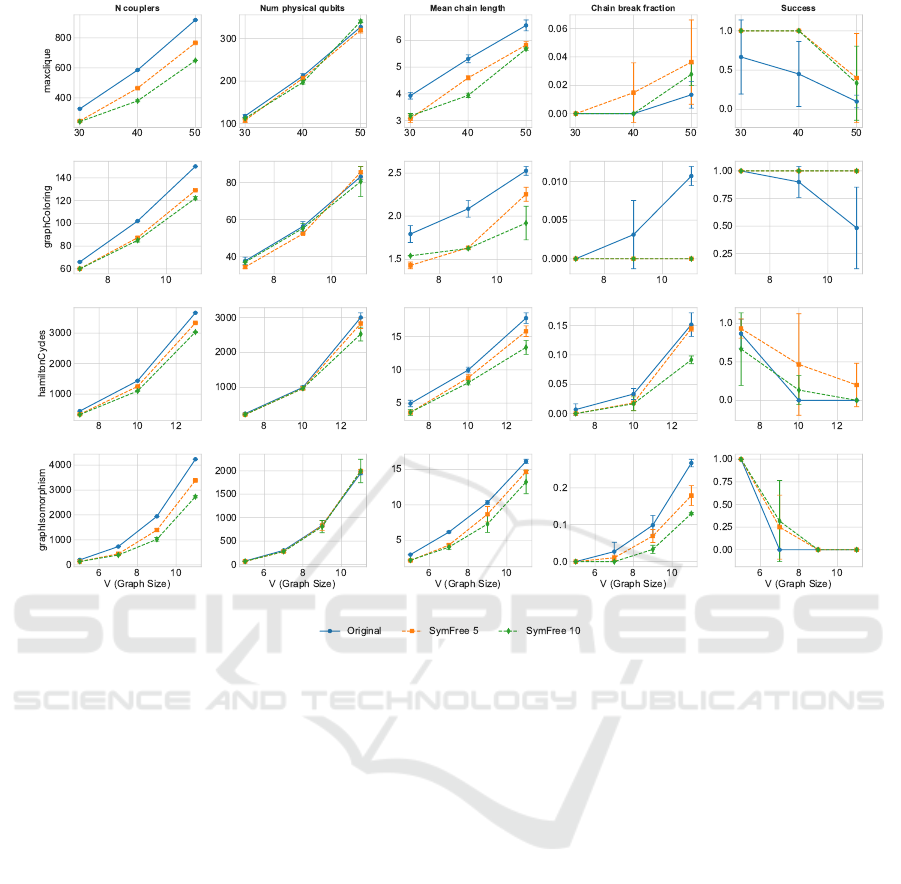
Figure 3: This ﬁgure presents the outcomes of our experiments on removing semi-symmetries using the algorithm described in

Section 3. We evaluated our approach on four optimization problems: Maximum Clique, Graph Coloring, Hamilton Cycles,

and Graph Isomorphism. Along the horizontal axis, the plot shows increasing problem size. We considered ﬁve metrics: the

number of couplings, the number of physical qubits, the mean chain length, the chain break fraction, and the success rate.

The success metric equals 1 whenever the annealer reaches the global optimum, as veriﬁed by a classical heuristic solver. Our

results indicate that removing semi-symmetries reduces the number of couplings, which in turn lowers the mean chain length.

This reduction leads to fewer chain breaks and ultimately improves the success rate.

Notably, the advantage of the symmetry-free ap-

proach became more pronounced at larger problem

sizes.

In summary, these experiments demonstrate

that leveraging semi-symmetry removal to produce

symmetry-free QUBOs can yield more hardware-

friendly embeddings. The resulting QUBOs generally

require fewer resources (couplers, physical qubits)

and produce higher-quality embeddings (shorter

chains, lower chain break fractions), ultimately

improving the probability of success. By making

problem instances more tractable for current quan-

tum annealers, our approach provides a practical

path toward better performance on larger and more

challenging optimization problems.

In a second experiment (see Figure 4), we ana-

lyzed the transpiled circuit depth of QAOA with

p = 1. Unlike the ﬁrst experiment, we factored

out all semi-symmetries. In the ﬁrst experiment,

we used a ﬁxed number of semi-symmetries, as

eliminating smaller semi-symmetries (e.g. fewer than

10 common couplings) typically does not improve

performance on quantum annealers. This is because

the additional physical qubits required to represent

the new logical (ancilla) qubits often exceed the

physical qubits saved by shortening the chains.

The results demonstrate that the real beneﬁt of our

approach becomes evident with larger problem sizes,

as these inherently contain more semi-symmetries.

As quantum hardware continues to advance, enabling

the solution of larger problem instances, this method

will become increasingly signiﬁcant. The ability to

effectively handle semi-symmetries at scale promises

substantial improvements in circuit depth and re-

source efﬁciency, highlighting the long-term rele-

vance of this technique beyond the currently solvable

problem instances.

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

790

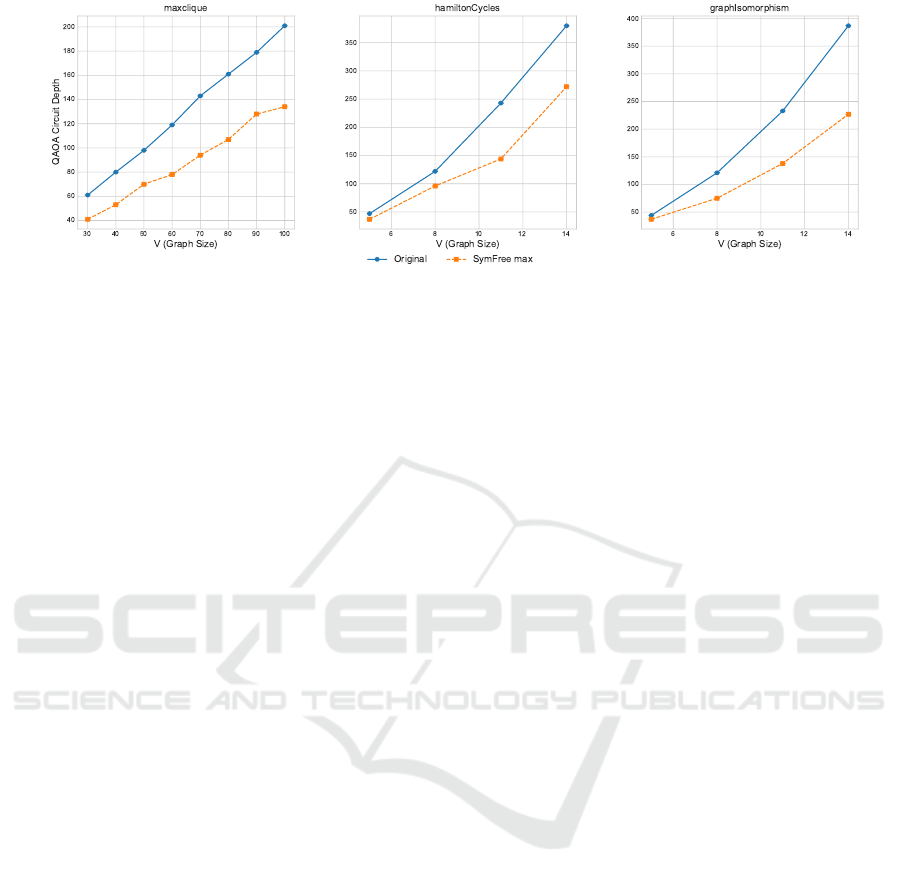
Figure 4: Comparison of QAOA circuit depth with and without semi-symmetry elimination for different graph problems:

MaxClique (left), HamiltonCycles (center), and GraphIsomorphism (right). The blue solid line (Original) represents the

circuit depth without symmetry elimination, while the orange dashed line (SymFree max) shows the results after factoring

out all semi-symmetries. The reduction in circuit depth becomes more pronounced for larger graph sizes, demonstrating the

efﬁciency of the semi-symmetry elimination approach.

For the empirical evaluation in the ﬁrst experi-

ment, we used the D-Wave Advantage 4.1 quantum

annealer, which features 5760 qubits. Each experi-

mental conﬁguration was executed over 10 runs, and

the standard deviation is reported in the results to il-

lustrate variability.

For the QAOA experiments, we transpiled the cir-

cuits using Qiskit Aer. However, the transpilation was

performed solely to measure circuit depth, as the re-

sulting circuits are too large to be executed or simu-

lated on available quantum hardware.

6 CONCLUSION

In this work, we introduced the concept of semi-

symmetries in QUBO matrices and proposed an al-

gorithm for identifying and factoring these symme-

tries into ancilla qubits. Our method effectively re-

duces the number of non-zero couplings in the QUBO

matrix, which directly translates to improvements in

both the Quantum Approximate Optimization Algo-

rithm (QAOA) and Quantum Annealing.

Theoretical analysis conﬁrmed that the modiﬁed

QUBO matrix Q

mod

retains the same energy spec-

trum as the original matrix Q, ensuring the correctness

of the optimization problem. Our experimental eval-

uations demonstrated signiﬁcant reductions in both

computational and physical resource requirements.

Speciﬁcally, our approach achieved up to a 45% re-

duction in couplings and QAOA circuit depth. For

Quantum Annealing, the reduced matrix structure led

to sparser problem embeddings, shorter qubit chains,

and improved overall performance.

The results were validated across a range of com-

binatorial optimization problems, including Maxi-

mum Clique, Hamilton Cycles, Graph Coloring, and

Graph Isomorphism, all of which naturally exhibit

semi-symmetries. The ﬁndings indicate that leverag-

ing such symmetries enhances the scalability and efﬁ-

ciency of quantum optimization algorithms, address-

ing key challenges such as circuit depth, error accu-

mulation, and embedding complexity.

Looking forward, as quantum hardware contin-

ues to advance, the ability to exploit matrix structure

for optimization problems will become increasingly

crucial. Our method provides a promising step to-

ward making quantum algorithms more practical and

scalable for real-world combinatorial problems. Fu-

ture work will explore further generalizations of semi-

symmetry detection, integration with higher-layer op-

timization frameworks, and broader applicability to

other classes of quantum algorithms.

ACKNOWLEDGMENT

This publication was created as part of the Q-Grid

project (13N16179) under the “quantum technologies

– from basic research to market” funding program,

supported by the German Federal Ministry of Educa-

tion and Research.

REFERENCES

Ahmed, S. (2012). Applications of graph coloring in mod-

ern computer science. International Journal of Com-

puter and Information Technology, 3(2):1–7.

Ayanzadeh, R., Alavisamani, N., Das, P., and Qureshi, M.

(2023). Frozenqubits: Boosting ﬁdelity of qaoa by

skipping hotspot nodes. In Proceedings of the 28th

ACM International Conference on Architectural Sup-

port for Programming Languages and Operating Sys-

tems, Volume 2, pages 311–324.

Reducing QUBO Density by Factoring out Semi-Symmetries

791

Bucher, D., N

ußlein, J., O’Meara, C., Angelov, I., Wimmer,

B., Ghosh, K., Cortiana, G., and Linnhoff-Popien,

C. (2023). Dynamic price incentivization for car-

bon emission reduction using quantum optimization.

arXiv preprint arXiv:2309.05502.

Eblen, J. D., Phillips, C. A., Rogers, G. L., and Langston,

M. A. (2011). The maximum clique enumeration

problem: Algorithms, applications and implementa-

tions. In International Symposium on Bioinformatics

Research and Applications, pages 306–319. Springer.

Farhi, E., Goldstone, J., and Gutmann, S. (2014). A

quantum approximate optimization algorithm. arXiv

preprint arXiv:1411.4028.

Farhi, E. and Harrow, A. W. (2016). Quantum supremacy

through the quantum approximate optimization algo-

rithm. arXiv preprint arXiv:1602.07674.

Glover, F., Kochenberger, G., and Du, Y. (2018). A tutorial

on formulating and using qubo models. arXiv preprint

arXiv:1811.11538.

Herrman, R., Treffert, L., Ostrowski, J., Lotshaw, P. C.,

Humble, T. S., and Siopsis, G. (2021). Impact of graph

structures for qaoa on maxcut. Quantum Information

Processing, 20(9):289.

Kawarabayashi, K.-i. (2001). A survey on hamiltonian cy-

cles. Interdisciplinary Information Sciences, 7(1):25–

39.

Laporte, G. and Mart

ın, I. R. (2007). Locating a cycle in a

transportation or a telecommunications network. Net-

works: An International Journal, 50(1):92–108.

Lee, X., Saito, Y., Cai, D., and Asai, N. (2021). Parameters

ﬁxing strategy for quantum approximate optimization

algorithm. In 2021 IEEE international conference

on quantum computing and engineering (QCE), pages

10–16. IEEE.

Lodewijks, B. (2020). Mapping NP-hard and NP-complete

optimisation problems to quadratic unconstrained bi-

nary optimisation problems.

Lu, X. On np-intermediate, isomorphism problems, and

polynomial hierarchy.

Lucas, A. (2014). Ising formulations of many np problems.

Frontiers in physics, 2:5.

Majumdar, R., Bhoumik, D., Madan, D., Vinayagamurthy,

D., Raghunathan, S., and Sur-Kolay, S. (2021). Depth

optimized ansatz circuit in qaoa for max-cut. arXiv

preprint arXiv:2110.04637.

Mooney, G., Tonetto, S., Hill, C., and Hollenberg, L.

(2019). Mapping NP-hard problems to restructed adi-

abatic quantum architectures.

Morita, S. and Nishimori, H. (2008). Mathematical founda-

tion of quantum annealing. Journal of Mathematical

Physics, 49(12).

Ni, X.-H., Cai, B.-B., Liu, H.-L., Qin, S.-J., Gao, F., and

Wen, Q.-Y. (2023). More efﬁcient parameter initial-

ization strategy in qaoa for maxcut. arXiv preprint

arXiv:2306.06986.

Niu, M. Y., Lu, S., and Chuang, I. L. (2019). Optimizing

qaoa: Success probability and runtime dependence on

circuit depth. arXiv preprint arXiv:1905.12134.

ußlein, J., Gabor, T., Linnhoff-Popien, C., and Feld, S.

(2022). Algorithmic qubo formulations for k-sat and

hamiltonian cycles. In Proceedings of the genetic

and evolutionary computation conference companion,

pages 2240–2246.

ußlein, J., Roch, C., Gabor, T., Stein, J., Linnhoff-Popien,

C., and Feld, S. (2023). Black box optimization using

qubo and the cross entropy method. In International

Conference on Computational Science, pages 48–55.

Springer.

Pan, Y., Tong, Y., Xue, S., and Zhang, G. (2022a). Efﬁcient

depth selection for the implementation of noisy quan-

tum approximate optimization algorithm. Journal of

the Franklin Institute, 359(18):11273–11287.

Pan, Y., Tong, Y., and Yang, Y. (2022b). Automatic depth

optimization for a quantum approximate optimization

algorithm. Physical Review A, 105(3):032433.

Ponce, M., Herrman, R., Lotshaw, P. C., Powers, S., Siop-

sis, G., Humble, T., and Ostrowski, J. (2023). Graph

decomposition techniques for solving combinatorial

optimization problems with variational quantum algo-

rithms. arXiv preprint arXiv:2306.00494.

Prasanna, D., Patton, R., Schuman, C., and Potok, T. (2019).

Efﬁciently embedding QUBO problems on adiabatic

quantum computers.

Roch, C., Ratke, D., N

ußlein, J., Gabor, T., and Feld, S.

(2023). The effect of penalty factors of constrained

hamiltonians on the eigenspectrum in quantum an-

nealing. ACM Transactions on Quantum Computing,

4(2):1–18.

Rossi, R. A., Gleich, D. F., and Gebremedhin, A. H. (2015).

Parallel maximum clique algorithms with applications

to network analysis. SIAM Journal on Scientiﬁc Com-

puting, 37(5):C589–C616.

Sax, I., Feld, S., Zielinski, S., Gabor, T., Linnhoff-Popien,

C., and Mauerer, W. (2020). Approximate approxima-

tion on a quantum annealer. In Proceedings of the 17th

ACM International Conference on Computing Fron-

tiers, pages 108–117.

Shaydulin, R. and Galda, A. (2021). Error mitigation

for deep quantum optimization circuits by leverag-

ing problem symmetries. In 2021 IEEE International

Conference on Quantum Computing and Engineering

(QCE), pages 291–300. IEEE.

Shaydulin, R., Hadﬁeld, S., Hogg, T., and Safro, I.

(2020). Classical symmetries and qaoa. arXiv preprint

arXiv:2012.04713.

Shaydulin, R. and Wild, S. M. (2021). Exploiting symmetry

reduces the cost of training qaoa. IEEE Transactions

on Quantum Engineering, 2:1–9.

Zielinski, S., N

ußlein, J., Stein, J., Gabor, T., Linnhoff-

Popien, C., and Feld, S. (2023a). Inﬂuence of differ-

ent 3sat-to-qubo transformations on the solution qual-

ity of quantum annealing: A benchmark study. In

Proceedings of the Companion Conference on Genetic

and Evolutionary Computation, pages 2263–2271.

Zielinski, S., N

ußlein, J., Stein, J., Gabor, T., Linnhoff-

Popien, C., and Feld, S. (2023b). Pattern qubos: Algo-

rithmic construction of 3sat-to-qubo transformations.

Electronics, 12(16):3492.

Zou, P. (2023). Multiscale quantum approximate optimiza-

tion algorithm. arXiv preprint arXiv:2312.06181.

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

792