Applying Quantum Tensor Networks in Machine Learning: A Systematic

Literature Review

Erico Souza Teixeira

1,2 a

, Yara Rodrigues Inácio

2,3 b

and Pamela T. L. Bezerra

2,3 c

CESAR, Recife, Brazil

|QAT S⟩ - Quantum Application in Technology and Software Group, Recife, Brazil

Computer Science, CESAR School, Recife, Brazil

Keywords:

Quantum Computing, Quantum Tensor Networks, Quantum Machine Learning, Quantum Advantage.

Abstract:

Integrating quantum computing (QC) into machine learning (ML) holds the promise of revolutionizing com-

putational efﬁciency and accuracy across diverse applications. Quantum Tensor Networks (QTNs), an ad-

vanced framework combining the principles of tensor networks with quantum computation, offer substantial

advantages in representing and processing high-dimensional quantum states. This systematic literature review

explores the role and impact of QTNs in ML, focusing on their potential to accelerate computations, enhance

generalization capabilities, and manage complex datasets. By analyzing 23 studies from 2013 to 2024, we

summarize key advancements, challenges, and practical applications of QTNs in quantum machine learning

(QML). Results indicate that QTNs can signiﬁcantly reduce computational resource demands by compressing

high-dimensional data, enhance robustness against noise, and optimize quantum circuits, achieving up to a 10-

million-fold speedup in speciﬁc scenarios. Additionally, QTNs demonstrate strong generalization capabilities,

achieving high classiﬁcation accuracy (up to 0.95) with fewer parameters and training data. These ﬁndings

position QTNs as a transformative tool in QML, bridging critical limitations in current quantum hardware and

enabling real-world applications.

1 INTRODUCTION

Quantum computing (QC) is a groundbreaking com-

putational paradigm that leverages the principles of

quantum mechanics to process information. Its fun-

damental unit, the qubit, can exist in a superposition

of states, representing both 0 and 1 simultaneously.

This property allows quantum computers to encode

and manipulate signiﬁcantly more information with

fewer units compared to classical systems. One of

QC’s most promising applications lies in accelerat-

ing the processing of large datasets and complex al-

gorithms, particularly in machine learning (ML). The

integration of quantum computing and ML, known as

quantum machine learning (QML), has the potential

to revolutionize ﬁelds such as pattern recognition, op-

timization, and data analysis (Tychola et al., 2023).

By utilizing quantum algorithms, QML aims to en-

hance the efﬁciency and accuracy of tasks like clas-

https://orcid.org/0000-0003-0520-5075

https://orcid.org/0009-0000-4340-4652

https://orcid.org/0000-0002-5067-1617

siﬁcation and regression, paving the way for trans-

formative advancements in data-driven technologies

(Tychola et al., 2023) (Manjunath et al., 2023).

Tensor Networks (TNs) are versatile mathemati-

cal frameworks widely used in physics and computer

science to model and analyze complex systems, such

as quantum many-body systems and neural networks

(Azad, 2024). A tensor network is composed of inter-

connected tensors and multi-dimensional arrays that

encode numerical data (Azad, 2024). Each tensor cor-

responds to a speciﬁc component or site within the

system, representing its states and capturing all pos-

sible conﬁgurations or conditions of that component

(Biamonte and Bergholm, 2017b).

This structured representation signiﬁcantly sim-

pliﬁes computational challenges by reducing the com-

plexity of operations such as evaluating the partition

function, a key measure summarizing the energy con-

ﬁgurations of a system in thermal equilibrium (Liu

et al., 2021). TNs are particularly well-suited for sys-

tems with numerous degrees of freedom, where tra-

ditional methods often struggle with scalability and

efﬁciency (Kardashin et al., 2021).

Teixeira, E. S., Inácio, Y. R. and Bezerra, P. T. L.

Applying Quantum Tensor Networks in Machine Learning: A Systematic Literature Review.

DOI: 10.5220/0013402100003890

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2025) - Volume 1, pages 847-854

ISBN: 978-989-758-737-5; ISSN: 2184-433X

847

Quantum Tensor Networks (QTNs) extend classi-

cal tensor networks, enabling the efﬁcient representa-

tion and manipulation of high-dimensional quantum

states (Rieser et al., 2023) (Hou et al., 2024). They

offer a robust framework for compressing and simpli-

fying large quantum systems, a capability that is es-

sential for managing the complexity inherent in quan-

tum computations (Biamonte and Bergholm, 2017a)

(Azad, 2024) (Liu et al., 2021).

Additionally, quantum computers operate within

the Noisy Intermediate-Scale Quantum (NISQ) era,

which is deﬁned by signiﬁcant hardware constraints

such as environmental noise, imperfect quantum

gates, and limited qubit availability. QTNs provide

a pathway to address these challenges by optimizing

quantum state representations, minimizing computa-

tional resource demands, and enhancing quantum er-

ror correction techniques. These advances facilitate

more efﬁcient utilization of the constrained resources

available in NISQ-era quantum hardware.

In the context of quantum machine learning

(QML), QTNs present promising solutions to founda-

tional challenges, including reducing representation

complexity for quantum systems and efﬁciently han-

dling large datasets. By leveraging QTNs, researchers

aim to enhance scalability and computational efﬁ-

ciency, overcoming critical limitations in quantum

computing performance while unlocking new oppor-

tunities for advancements in machine learning appli-

cations (Biamonte and Bergholm, 2017a) (Liu et al.,

2021). Consequently, developing QTNs represents a

pivotal step in integrating quantum computing (QC)

with machine learning (ML), fostering progress at the

intersection of these transformative ﬁelds.

Despite its potential, there is a lack of understand-

ing of QTNs practical applications due to its recent

emergence, which demands a proper systematic liter-

ature review (SLR) to explore its beneﬁts and poten-

tial uses. This review might reveal effective meth-

ods, address challenges, and highlight progress in

quantum computing, offering valuable insights for

researchers aiming to fully harness QTNs potential

(Guala et al., 2023).

As far as we know, there is no SLR on Quantum

Tensor Networks and their applications in Quantum

Machine Learning. This paper aims to ﬁll this gap by

investigating and summarizing the main applications

and challenges of QTN. By doing so, we seek to pro-

vide a clearer understanding of the potential of QTN

in QML and guide future research in this emerging

ﬁeld. This paper is organized as follows: Section 2

details the deﬁnition of Tensor Networks, QTN, and

QML; Section 3 summarizes the SRL steps; Sec-

tion 4 describes the key observations obtained from

the SRL and ﬁnally Section 5 brings this research

main conclusion and the necessary future steps.

2 BACKGROUND

2.1 Tensor Networks

Tensor Networks (TN) operate using tensors, an ex-

tension of traditional data structures like matrices

and vectors (Bridgeman and Chubb, 2016) (Bañuls,

2023), representing systems through interconnected

smaller tensors (nodes) connected by edges (Sen-

gupta et al., 2022). This structure allows TN to ef-

fectively represent multidimensional real-world data,

making them suitable for modeling complex phenom-

ena across various disciplines (Cores et al., 2024).

Additionally, TNs excel in handling structured and

hierarchical data, providing comprehensive, contex-

tual representations that reveal complex patterns and

subtle interactions between variables (Cores et al.,

2024), making them invaluable for solving computa-

tional challenges across different research ﬁelds.

There are various types of TNs, but three are es-

pecially important: Matrix Product States (MPS),

the most famous example of TN states due to its

underlying powerful methods for simulating many-

body quantum systems in one dimension, such as the

Density Matrix Renormalization Group (DMRG) al-

gorithm. (Orús, 2014); Projected Entangled Pair

States (PEPS) it’s deﬁned by a network of three-

dimensional tensors similar to the MPS network,

but with the addition of a set of binding tensors

that connect them (Orús, 2014). PEPS is used

for two-dimensional systems, which extends the ef-

ﬁciency and power of MPS to higher-dimensional

quantum systems and is, therefore, relevant for

describing complex physical phenomena; and ﬁ-

nally The Multi-scale Entanglement Renormaliza-

tion Ansatz (MERA), a tensor network framework

designed to represent strongly correlated quantum

many-body states efﬁciently. MERA uses a hierar-

chical organization of tensors to capture entanglement

across multiple scales, making it especially useful for

simulating quantum ﬁeld theories. It has also been

adapted for computational methods like variational

Monte Carlo and applications in QML (Rieser et al.,

2023) (Bhatia and Kumar, 2018).

Apart from these types, Tree Tensor Network

(TTN), is especially relevant for this SLR because

it is a hierarchical model used to efﬁciently repre-

sent quantum states by decomposing them into a tree-

like structure of tensors. Each tensor in the net-

work represents a local part of the quantum state, and

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

848

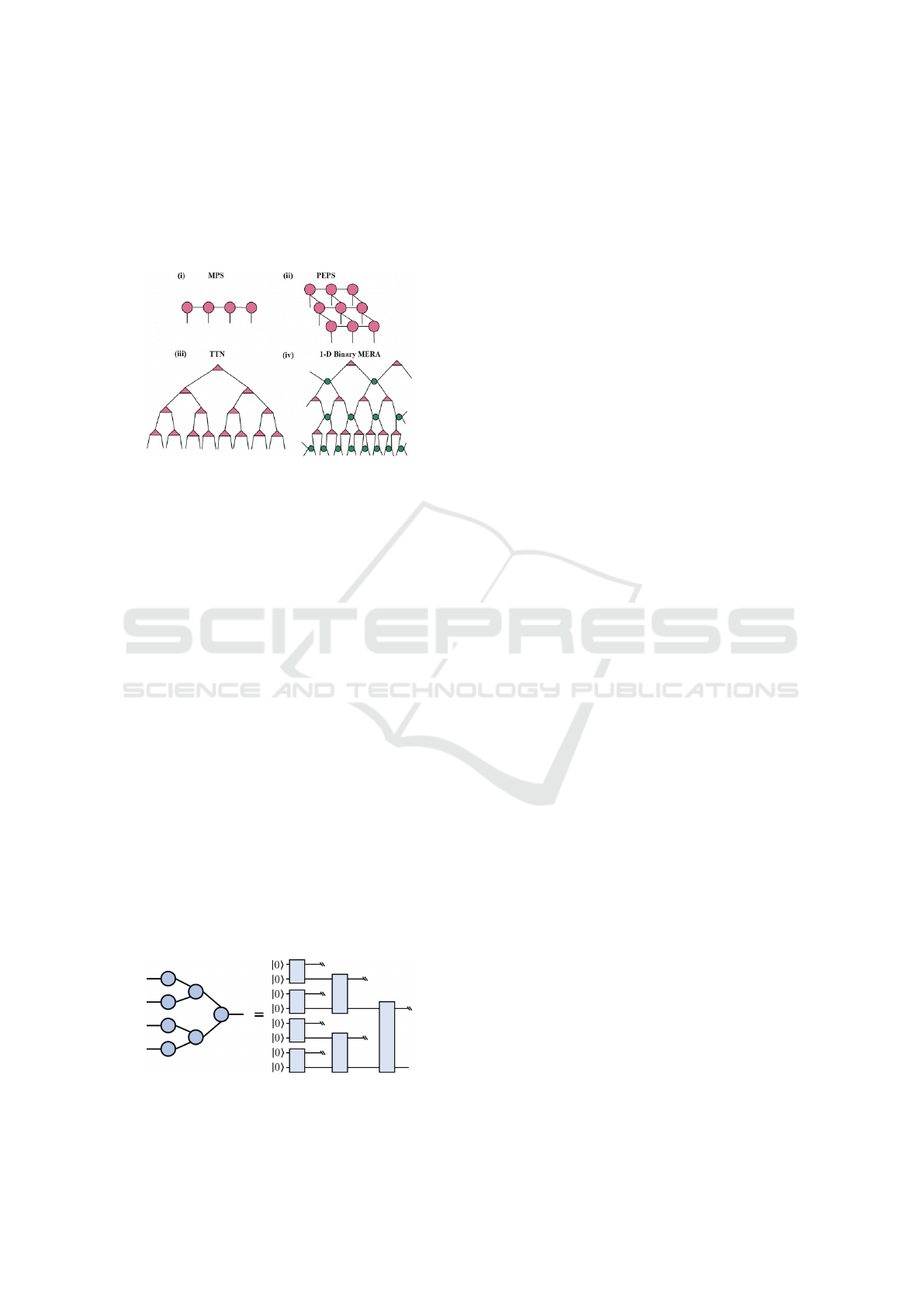
the connectivity between tensors reﬂects the correla-

tions between those parts. This structure allows for

the efﬁcient representation and manipulation of high-

dimensional quantum states, particularly in systems

with strong local correlations (Rieser et al., 2023).

The structure of these TNs is detailed in Figure 1.

Figure 1: Types of TN (Bhatia and Kumar, 2018)).

2.2 Quantum Tensor Networks

Quantum Tensor Networks (QTNs) are an extension

of classical tensor networks, speciﬁcally designed for

quantum systems, enabling efﬁcient representation

and manipulation of complex quantum states (Bia-

monte and Bergholm, 2017a). They play a signiﬁcant

role in developing algorithms for small-scale quan-

tum computers, especially those with limited qubit re-

sources. Furthermore, while QTNs are not inherently

resistant to noise, they provide a powerful framework

that can be integrated with quantum error correction

methods, which are crucial in the NISQ era, where

quantum hardware is prone to noise and limited qubit

coherence.

One key feature of QTNs is their ability to rep-

resent quantum circuits, where each qubit and quan-

tum gate operation is associated with a speciﬁc tensor,

with the tensor network capturing the interactions and

entanglement between qubits. This allows the tempo-

ral evolution of a quantum system governed by quan-

tum gates to be effectively expressed within a QTN

framework. Figure 2 illustrates how quantum circuits

and QTNs are closely related, providing a clear map-

ping between the two concepts.

Figure 2: Quantum circuit based on QTN (Guala et al.,

2023)).

Popular examples of QTN include Quantum Ma-

trix Product States (QMPS) (Adhikary et al., 2021),

which is a compact representation of often intractable

wave functions of complex quantum systems, such as

Quantum Tensor Train Networks. It is designed for

efﬁciently describing two-dimensional systems; and

Quantum Multi-scale Entanglement Renormaliza-

tion Ansatz (QMERA), a more general approach that

represents quantum systems with multiple entangle-

ment scales. These QTN approaches have become

essential tools for simulating quantum systems, opti-

mizing quantum algorithms, and exploring the struc-

ture of quantum states, underscoring their value in ad-

vancing the ﬁeld of quantum computation.

2.3 Quantum Machine Learning

Quantum Machine Learning (QML) is a research ﬁeld

that integrates quantum computing principles with

machine learning techniques to tackle computational

challenges more efﬁciently. Quantum computing uti-

lizes phenomena like superposition and entanglement

to process and store information in fundamentally

novel ways. By leveraging these quantum proper-

ties, QML aims to enhance tasks such as classiﬁ-

cation, regression, clustering, and optimization, par-

ticularly in scenarios involving large and complex

datasets (Huang et al., 2021a).

3 METHODOLOGY

This research employs a systematic literature review

(SLR) approach to investigate the state of the art in

quantum computing (QC), QTN, and QML. Follow-

ing the guidelines proposed by Xiao and Watson in

(Xiao and Watson, 2019), this review addresses spe-

ciﬁc research questions through a documented and

reproducible process, emphasizing methodological

rigor in data collection and synthesis stages. The hy-

pothesis "The incorporation of Quantum Tensor Net-

works into Quantum Machine Learning algorithms

has the potential to bring about signiﬁcant advances

in terms of computational speed, generalization ca-

pability, and efﬁcient handling of complex data." was

developed to address the following research question:

• Can Quantum Tensor Networks (QTN) demon-

strate tangible beneﬁts in Quantum Machine

Learning (QML) applications?

Table 1 describes the databases explored, the

search string developed, and the number of papers ob-

tained in each SRL stage (from the initial search to the

selected papers). This search focused on databases

Applying Quantum Tensor Networks in Machine Learning: A Systematic Literature Review

849

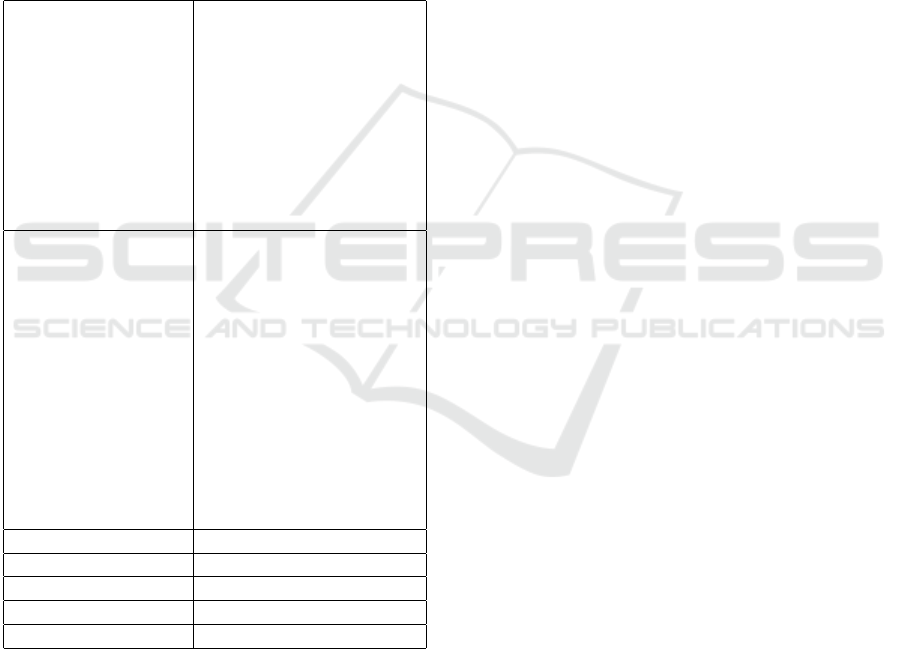
highly impacting scientiﬁc research, quantum tech-

nologies, and gray literature. Initially, the search

string focused only on the work’s abstract and title.

To reﬁne the results, only articles written in English

were considered, as English is a widely accepted uni-

versal language for research. Additionally, we lim-

ited the search scope to studies published since 2013

to ensure we included the most current technologies,

approaches, and solutions in the ﬁeld. The search

was concluded on August 17th, 2024, so articles pub-

lished after this date were not considered, aligning

with the deadlines for writing and submitting this ma-

terial. This initial search returned 7967 documents.

Table 1: Details on the databases and search string used in

the SRL.

DATABASES - Google Scholar

- IEEE Xplore

- DOAJ

- SpringerLink

- IOPscience

- MDPI

- ScienceDirect

- Annual Reviews

- Pennylane

- Quantinuum

SEARCH STRING ABS(("Abstract":"Quantum

Computing" OR "Ab-

stract":"Quantum Ten-

sor Networks") AND

("Abstract":"Quantum

Machine Learn-

ing" AND ("Ab-

stract":"computational

speed" OR "Ab-

stract":"generalization

capability" OR "Ab-

stract":"handling of

complex data")))

Initial Search 7967

FILTER I 346

FILTER II 121

FILTER III 72

Selected Documents 23

Inclusion and exclusion criteria for the document

search were established to ensure the relevance and

quality of the selected studies. Both criteria were ap-

plied with a detailed explanation of their meaning dur-

ing the selection process, clearly specifying the ac-

ceptance and rejection factors. This strategy aims to

enhance transparency and reduce subjectivity in each

ﬁlter. For this search, three stages were deﬁned to

gradually ﬁlter the most relevant work for the SLR,

each requiring different reading depths. Details are

described as follows:

FILTER I: TITTLE - Aim to ﬁlter Academic

Studies on Quantum Computing in Machine Learning

or Tensor Networks by their titles.

• Includes: Studies speciﬁcally discussing Quan-

tum Tensor Networks (QTNs) and their appli-

cation in Quantum Machine Learning tasks like

classiﬁcation and regression.

• Excludes:

Studies unrelated to quantum computing, quan-

tum tensor networks or quantum machine learn-

ing, studies not focused on the speciﬁed tasks, or

those focusing solely on classical applications.

After applying this ﬁlter, the number of works was

reduced from 7,967 to 346.

FILTER II: ABSTRACT - Aims to ﬁlter Aca-

demic Studies on Quantum Computing in Machine

Learning or Tensor Networks or Tensor Networks by

their abstract.

• Includes: Research papers, reviews, theses, and

articles discussing integrating quantum comput-

ing techniques and tensor networks into Quantum

Machine learning algorithms.

• Excludes: Studies that do not address quantum

computing, machine learning, tensor networks, or

their combination.

By narrowing the selection to studies that discuss

integrating quantum computing techniques into ma-

chine learning algorithms, the number of documents

was further reduced from 346 to 121.

Filter III: TEXT Aims to ﬁlter Academic Stud-

ies on Quantum Computing in Machine Learning or

Tensor Networks by reading the complete text.

• Includes: Full-text articles, papers, and reports

accessible for review.

• Excludes: Texts that are inaccessible or require

special permissions for access.

Finally, the selection was limited to full-text arti-

cles and reports accessible for review, resulting in 72

documents.

The number of returned documents was observed

to ensure the validity of the systematic review. Ulti-

mately, 23 articles were selected for the analysis after

thoroughly reviewing the 72 ﬁltered articles, elimi-

nating those that did not directly answer the research

question. We focused on papers that implemented

and tested QTN in different scenarios, clearly show-

ing through experiments and comparative analysis the

many beneﬁts of QTN in QML.

While there is no strict rule, more than 30% of

the ﬁltered articles are often considered adequate for

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

850

comprehensive analysis in such reviews, indicating a

robust selection process. This quantity not only en-

hances the reliability of the review but also supports

the overall quality of the ﬁndings.

Data extraction is the ﬁnal step following the

search and ﬁltering stages. It involves extracting

the necessary information about computational speed,

generalization capability, and complex data handling

through detailed reading to validate or refute the hy-

potheses. The extracted information is organized into

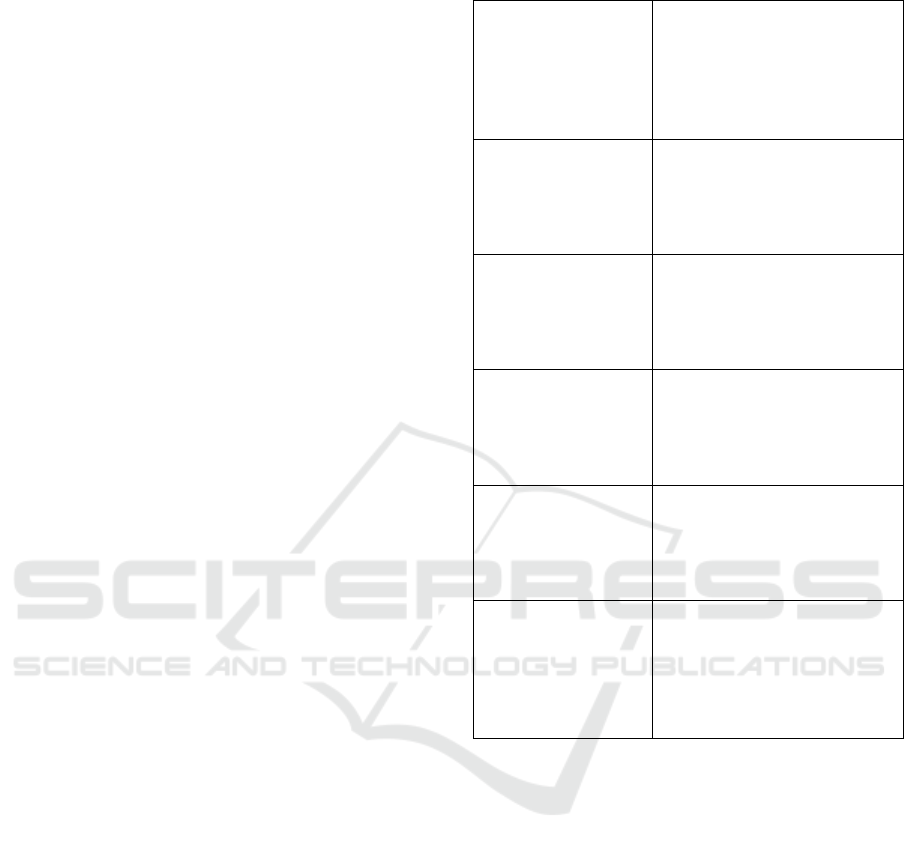
topics related to the inclusion criteria as shown in Ta-

ble 2. The purpose of this list is to ensure that all

relevant aspects are covered and to facilitate analysis.

To address the research question guiding this SLR,

we seek speciﬁc insights from the analyzed papers.

The exploration of QML application areas focuses on

identifying domains such as supervised learning or

classiﬁcation, enabling a comprehensive understand-

ing of QML’s practical scope. Algorithm performance

is assessed using metrics like accuracy and reliability

to evaluate the effectiveness of QML models and pin-

point areas for improvement.

A critical aspect of the analysis is computational

speed, which examines the time efﬁciency of QML

algorithms compared to classical counterparts, high-

lighting a core advantage of QTNs. The generaliza-

tion capacity of QML models, reﬂecting their ability

to reliably perform on unseen data, is another key fac-

tor, as it determines scalability and suitability for real-

world deployment.

Efﬁciency in handling complex data is also evalu-

ated, emphasizing QML’s capability to process large,

high-dimensional datasets—a domain where QTNs

could offer substantial beneﬁts. The resource de-

mands for model training are examined to understand

the feasibility of implementing QML compared to

classical methods. Lastly, post-implementation ben-

eﬁts assess practical experimentations, demonstrating

how QML solutions can deliver meaningful outcomes

such as improved decision-making or cost reductions,

ultimately showcasing the practical value of incorpo-

rating QTN.

4 RESULTS AND DISCUSSIONS

In this section, we discuss the main ﬁndings of the

SLR. As mentioned, after applying inclusion and ex-

clusion criteria and reading the papers completely, 23

studies were selected due to their relevance to answer-

ing the research question. In the following sections,

we highlight the observed advantages of QTN in ef-

ﬁciently dealing with high-level data and enhancing

QML performance, as well as the current applications

Table 2: Key information analyzed during data extraction.

Areas explored in

QML

Focuses on the speciﬁc

domains (e.g., supervised

learning, classiﬁcation)

where QML is applied,

providing insights into its

broader applications.

Algorithm perfor-

mance

Evaluates the effectiveness

of QML algorithms through

metrics like accuracy and

reliability, revealing their

strengths and limitations.

Computational

Speed

Assesses the time efﬁciency

of QML algorithms, espe-

cially compared to classical

methods, to determine com-

putational advantages.

Generalization Ca-

pacity

Examines how well QML

models adapt to new data,

which is essential for practi-

cal application and reliabil-

ity.

Efﬁciency in Han-

dling Complex

Data

Looks at QML’s ability

to process large or high-

dimensional datasets, a

signiﬁcant advantage over

classical approaches.

Post-

implementation

beneﬁts

Analyzes the advantages of

QML in practical exper-

imentations, such as im-

proved decision-making and

cost savings, supporting its

practical value

of these networks.

4.1 QTN Advantages

QTN is particularly beneﬁcial in QML because it

can compress high-dimensional data, signiﬁcantly

reducing the computational and memory resources

needed to represent and manipulate large datasets.

Studies by (Araz and Spannowsky, 2022) (Orús,

2019) (Rieser et al., 2023) (Huggins et al., 2019)

highlight how QTNs offer efﬁcient data compres-

sion techniques that signiﬁcantly reduce memory and

computational requirements and excel at represent-

ing and manipulating high-dimensional datasets while

maintaining computational feasibility. For example,

(Huggins et al., 2019) indicates that using QTNs for

processing data like an 8 × 8 pixel image for hand-

writing recognition tasks can allow the number of

physical qubits needed to scale logarithmically with

the size of the processed data, whereas previously it

Applying Quantum Tensor Networks in Machine Learning: A Systematic Literature Review

851

scaled linearly.

In addition to enhancing the representational ef-

ﬁciency of high-dimensional data, QTNs also help

overcome other issues, such as barren plateaus, by

employing local loss functions, which optimize the

training landscape (Rieser et al., 2023). For exam-

ple, in a scenario where a classical model faced a bar-

ren plateau, the loss function showed minimal gra-

dient updates, leading to stagnation in training with

a plateau observed at a loss value of 0.3. However,

applying QTN with local loss functions did not en-

counter the same plateau effect, resulting in a more fa-

vorable training landscape and achieving a loss value

improving down to 0.15 (Rieser et al., 2023).

Moreover, QTNs offer signiﬁcant advantages in

simulating large-scale quantum circuits. Unlike

traditional state vector methods, which scale expo-

nentially with the number of qubits, QTNs leverage

tensor contractions that are optimized through rear-

ranged contraction sequences, thereby reducing mem-

ory requirements and computational costs (Lykov,

2024). For example, applying a diagonal representa-

tion of quantum gates decreased tensor network con-

traction’s complexity by one to four orders of magni-

tude. By optimizing the conversion of the QAOA cir-

cuit into a tensor network and using techniques like

the greedy algorithm from the QTensor package, cal-

culating a single amplitude of the QAOA ansatz state

had a signiﬁcant improvement in terms of computa-

tional speed, achieving a speedup of up to 10 million

times. This optimization allowed for the simulation of

larger QAOA circuits, increasing the number of qubits

from 180 to 244 on a supercomputer (Lykov, 2024).

Another signiﬁcant advantage of QTNs in QML

is their ability to effectively model effectively

model complex quantum correlations, a feature

that enables improved generalization in QML models

(Rieser et al., 2023). QTNs achieve this balance be-

tween complexity and tractability through adjustable

bond dimensions, which deﬁne the maximum number

of states that can be represented at the interfaces be-

tween tensors. These bond dimensions determine the

network’s capacity to represent quantum states while

inﬂuencing the structure and variety of the tensor net-

work (Bernardi et al., 2022). By tuning these param-

eters, QTNs mitigate risks associated with complex

datasets, such as overﬁtting (Huggins et al., 2019).

As demonstrated in studies by Rieser, Köster, and

Raulf (Rieser et al., 2023), QTNs not only enhance

generalization to unseen data but also provide ro-

bustness against noise — a critical challenge in quan-

tum computing. For instance, research in (Rieser

et al., 2023) and (Huggins et al., 2019) highlights

how QTNs enable higher accuracy with less training

data: with the MNIST dataset and the model used

for digit classiﬁcation, the accuracy was 0.88 using

the full dataset of 60,000 images. However, apply-

ing the model with QTN, the accuracy was reduced

to approximately 0.806, still an high value, but with

the dataset size reduced to 20%, all while demon-

strating resilience to noise. Furthermore, the hierar-

chical structure of QTNs facilitates the representation

of weight parameters in machine learning algorithms,

making them a powerful and efﬁcient tool for process-

ing and analyzing complex datasets (Huggins et al.,

2019). Moreover, (Rieser et al., 2023) indicated that

QTN classiﬁers can achieve high classiﬁcation ac-

curacies ranging from 0.85 to 0.95 while utilizing a

limited number of parameters and internal qubits and

suggests that the structured nature of QTNs may fa-

cilitate easier training through local optimization rou-

tines QTNs can efﬁciently capture relevant patterns in

data with a reduced amount of training data required.

4.2 QTN Applications

QTNs are primarily applied in QML for quantum

classiﬁcation and feature extraction tasks. The work

in (Araz and Spannowsky, 2022) evaluated the per-

formance of Classical Tensor Networks (TN) and

their quantum counterparts (QTN) in classifying sim-

ulated Large Hadron Collider (LHC) data, focus-

ing on top jet discrimination against the QCD back-

ground. The results demonstrated that QML mod-

els combined with QTNs outperformed classical TN-

based approaches. For instance, classical TNs re-

quired signiﬁcantly more parameters— up to 64,800

in some conﬁgurations — to achieve competitive per-

formance. At the same time, QTNs attained superior

AUC values (e.g., 0.914 for Q-MERA) with as few

as 17 parameters. Moreover, QTNs achieved this ef-

ﬁciency using only 10,000 training events, compared

to 50,000 events required by classical TNs (Araz and

Spannowsky, 2022). These ﬁndings underscore the

advantages of QML models leveraging QTNs in terms

of parameter efﬁciency and performance, particularly

in high-energy physics applications (Araz and Span-

nowsky, 2022).

Variational Quantum Tensor Networks (VQTN)

are designed to operate effectively on near-term quan-

tum processors (Huang et al., 2021b). The VQTN

classiﬁer excels in tasks like classiﬁcation by com-

bining quantum and classical processing. While tra-

ditional QML algorithms like quantum principal com-

ponent analysis or quantum linear regression lever-

age quantum properties solely for speed, the VQTN’s

hybrid model incorporates a classical neural network

for processing output from quantum tensor networks.

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

852

Additionally, the algorithm employs kernel encoding,

circuit models, multiple readouts, and stochastic gra-

dient descent to reduce quantum circuit complexity

and improve performance.

Experimental results demonstrate that VQTN re-

duces the number of qubits needed while achieving

higher accuracy rates than the traditional QTN algo-

rithm. Tested on Iris and MNIST datasets, using TTN

models in its architecture, VQTN uses half the num-

ber of qubits compared to QTN while maintaining

an average accuracy of 93.72%. Compared with the

QTN algorithm, the accuracy is improved by 7.71%

(Huang et al., 2021b). Thus, VQTN serves as a bridge

that effectively enhances computational speed and ca-

pacity for complex data analysis, which may not be

achievable with isolated QML algorithms.

Another notable application of QTNs lies in Nat-

ural Language Processing (NLP). Researchers at

Quantinuum achieved a signiﬁcant breakthrough by

successfully running scalable quantum natural lan-

guage processing (QNLP) models on quantum hard-

ware (Quantinuum, 2024). Their tensor-network-

based approach incorporates syntax awareness into

the models, offering enhanced interpretability while

reducing the number of parameters and gate oper-

ations required. Experimental results indicate that

QNLP models running on current quantum devices

achieve prediction accuracy comparable to neural-

network-based classiﬁers, demonstrating the practical

viability of these models (Quantinuum, 2024).

The experiments further utilized advanced mod-

els, including the unitary structured tensor network

(uSTN) and the relaxed, structured tensor network

(rSTN), both of which delivered strong performance

across various NLP tasks (Quantinuum, 2024). No-

tably, the implementation of qubit reuse strategies en-

abled the compression of a 64-qubit uCTN circuit into

an 11-qubit circuit, signiﬁcantly optimizing resource

usage. This efﬁcient utilization of quantum hardware

underscores the potential of tensor network models

to enable sequence classiﬁcation tasks on near-term

quantum devices, paving the way for more resource-

efﬁcient and scalable quantum NLP applications.

A novel approach has been developed for embed-

ding continuous variables into quantum circuits using

piecewise polynomial features. This method, called

Piecewise Polynomial Tensor Network Quantum Fea-

ture Encoding (PPTNQFE), aims to enhance the ca-

pabilities of QML models by integrating continuous

variables into quantum circuits (Ali and Kabel, 2024).

This method leverages low-rank TN to create spatially

localized representations, making it particularly suit-

able for numerical applications like partial differential

equations (PDEs) and function regression.

The efﬁcacy of PPTNQFE is demonstrated

through two applications in one-dimensional scenar-

ios (Ali and Kabel, 2024). Firstly, it enables ef-

ﬁcient point evaluations of discretized solutions to

PDEs; speciﬁcally, compared to traditional rotation-

based encoding methods, which can require expo-

nential resources for representing similar data, PPT-

NQFE signiﬁcantly reduces complexity by leverag-

ing tensor networks, thus improving the efﬁciency of

quantum algorithms in PDE solving. A second ap-

plication is in function regression tasks, particularly

for modeling localized features like jump discontinu-

ities. Conventional approaches often struggle with pe-

riodicity and noise sensitivity, leading to inaccurate

approximations. In jump function tests, PPTNQFE

provided more accurate approximations using fewer

parameters, simplifying training and deployment pro-

cesses (Ali and Kabel, 2024).

5 CONCLUSIONS

This paper presented an SRL on the use of QTNs

in QML. The primary objective was to address the

research question: Can Quantum Tensor Networks

demonstrate tangible beneﬁts in quantum machine

learning applications? Through a comprehensive

analysis of 23 selected studies, we validated the hy-

pothesis that QTNs signiﬁcantly enhance machine

learning by leveraging the unique capabilities of

quantum computing.

The ﬁndings reveal that QTNs offer several key

advantages in QML. Firstly, they excel in compress-

ing high-dimensional data, which signiﬁcantly re-

duces computational and memory requirements. This

capability is particularly beneﬁcial for handling large

datasets, enabling more efﬁcient processing and stor-

age. Secondly, QTNs enhance computational speed,

achieving up to a 10-million-fold speedup in speciﬁc

scenarios, such as simulating large-scale quantum cir-

cuits. Thirdly, QTNs improve the generalization ca-

pabilities of QML models, allowing them to perform

reliably on unseen data with fewer parameters and

less training data.

Moreover, QTNs have shown promise in model-

ing complex quantum correlations, which enhances

their ability to capture patterns in data. This feature,

combined with their hierarchical structure, makes

QTNs a powerful tool for tasks such as classiﬁcation,

feature extraction, and NLP. Applications in high-

energy physics, variational QTNs, and QNLP have

demonstrated the practical viability of QTNs, show-

casing their potential to outperform classical methods

in terms of parameter efﬁciency and accuracy.

Applying Quantum Tensor Networks in Machine Learning: A Systematic Literature Review

853

Despite these advancements, several challenges

remain. The implementation of QTNs on near-term

quantum devices requires further optimization to ad-

dress hardware constraints, such as limited qubit co-

herence and noise. Additionally, more systematic

benchmarking against classical and QML approaches

is needed to fully understand the trade-offs and ad-

vantages of QTNs.

In conclusion, the incorporation of QTNs into

QML has the potential to drive signiﬁcant advance-

ments in computational efﬁciency, generalization, and

data handling. Continued development and explo-

ration of QTNs will not only advance the ﬁeld of

quantum machine learning but also contribute to the

broader landscape of computational science, paving

the way for transformative quantum technologies.

ACKNOWLEDGEMENTS

This work has been supported by CESAR - Centro de

Estudos e Sistemas Avançados do Recife - and CE-

SAR School.

REFERENCES

Adhikary, S., Srinivasan, S., Miller, J., Rabusseau, G., and

Boots, B. (2021). Quantum tensor networks, stochas-

tic processes, and weighted automata. Proceedings of

the 24th International Conference on Artiﬁcial Intelli-

gence and Statistics (AISTATS), 130:2080–2088.

Ali, M. and Kabel, M. (2024). Piecewise polynomial tensor

network quantum feature encoding. arXiv (Cornell

University).

Araz, J. Y. and Spannowsky, M. (2022). Classical versus

quantum: Comparing tensor-network-based quantum

circuits on large hadron collider data. Physical Review

A, 106(6).

Azad, F. (2024). Tensor networks for classical and quan-

tum simulation of open and closed quantum systems.

PhD thesis, University Coll. London, University Coll.

London.

Bañuls, M. C. (2023). Tensor network algorithms: A route

map. Annual Review of Condensed Matter Physics,

14(1):173–191.

Bernardi, A., Lazzari, C. D., and Gesmundo, F. (2022). Di-

mension of tensor network varieties. Communications

in Contemporary Mathematics, 25(10).

Bhatia, A. S. and Kumar, A. (2018). Quantifying ma-

trix product state. Quantum Information Processing,

17(3).

Biamonte, J. and Bergholm, V. (2017a). Quantum Tensor

Networks in a Nutshell.

Biamonte, J. and Bergholm, V. (2017b). Tensor networks in

a nutshell. arXiv (Cornell University).

Bridgeman, J. C. and Chubb, C. T. (2016). Hand-waving

and interpretive dance: an introductory course on ten-

sor networks. Journal of Physics A: Mathematical and

Theoretical, 50(22):223001–223001.

Cores, C. F., Kristjuhan, K., and Jones, M. N. (2024). A

joint optimization approach of parameterized quan-

tum circuits with a tensor network.

Guala, D., Zhang, S., Cruz, E., Riofrío, C. A., Klepsch,

J., and Arrazola, J. M. (2023). Practical overview of

image classiﬁcation with tensor-network quantum cir-

cuits. Scientiﬁc Reports, 13(1):4427.

Hou, Y.-Y., Li, J., Xu, T., and Liu, X.-Y. (2024). A

hybrid quantum-classical classiﬁcation modelbased

on branching multi-scale entanglementrenormaliza-

tion ansatz. Research Square (Research Square).

Huang, H. Y., Broughton, M., and Mohseni, M. e. a.

(2021a). Power of data in quantum machine learning.

Nature Communications, 12:2631.

Huang, R., Tan, X., and Xu, Q. (2021b). Variational

quantum tensor networks classiﬁers. Neurocomput-

ing, 452:89–98.

Huggins, W., Patil, P., Mitchell, B., Whaley, K. B., and

Stoudenmire, E. M. (2019). Towards quantum ma-

chine learning with tensor networks. Quantum Sci-

ence and Technology, 4(2):024001.

Kardashin, A., Uvarov, A., and Biamonte, J. (2021). Quan-

tum machine learning tensor network states. Frontiers

in Physics, 8.

Liu, X.-Y., Zhao, Q., Biamonte, J., and Walid, A. (2021).

Tensor, tensor networks, quantum tensor networks in

machine learning: An hourglass architecture.

Lykov, D. (2024). Large-scale tensor network quantum al-

gorithm simulator. Knowledge UChicago.

Manjunath, T. C., Venkatesan, M., and Prabhavathy, P.

(2023). Research oriented reviewing of quantum ma-

chine learning. International Research Journal on Ad-

vanced Science Hub, 5(Issue 05S):165–177.

Orús, R. (2014). A practical introduction to tensor net-

works: Matrix product states and projected entan-

gled pair states. Annals of Physics, 349(0003-

4916):117–158.

Orús, R. (2019). Tensor networks for complex quantum

systems. Nature Reviews Physics, 1(9):538–550.

Quantinuum (2024).

Rieser, H.-M., Köster, F., and Raulf, A. P. (2023). Tensor

networks for quantum machine learning. Proceedings

of the Royal Society A: Mathematical, Physical and

Engineering Sciences, 479(2275):20230218.

Sengupta, R., Adhikary, S., Oseledets, I., and Biamonte, J.

(2022). Tensor networks in machine learning.

Tychola, K. A., Kalampokas, T., and Papakostas, G. A.

(2023). Quantum machine learning—an overview.

Electronics, 12(11):2379.

Xiao, Y. and Watson, M. (2019). Guidance on conducting

a systematic literature review. Journal of Planning

Education and Research, 39(1):93–112.

QAIO 2025 - Workshop on Quantum Artiﬁcial Intelligence and Optimization 2025

854