Towards Big OLAP Data Cube Classification Methodologies:

The ClassCube Framework

Alfredo Cuzzocrea

1,2 a

and Mojtaba Hajian

iDEA Lab, University of Calabria, Rende, Italy

Department of Computer Science, University of Paris City, Paris, France

Keywords: Big Data Analytics, Multidimensional Big Data Analytics, Integration of OLAP Analysis and Classification.

Abstract: Focusing on the emerging big data analytics scenario, this paper introduces ClassCube, an innovative

methodology that combines OLAP analysis and classification algorithms for improving effectiveness,

expressive power and accuracy of the main classification task over big datasets shaped in the form of big

OLAP data cubes. The key idea of ClassCube relies on dimensionality reduction tools, which are deeply

investigated in this paper.

1 INTRODUCTION

In today’s data-driven era, organizations across

various sectors, such as finance, healthcare, and e-

commerce, rely heavily on analyzing large,

multidimensional datasets to make strategic decisions.

In this context, Online Analytical Processing (OLAP)

data cubes have become fundamental tools, enabling

complex queries and interactive exploration of data

aggregate over multiple dimensions. These data cubes

facilitate operations like slicing, dicing, and drilling

down into data, which are essential for uncovering

patterns and trends that lead to business insights.

However, as the volume and dimensionality of

data continue to grow exponentially, performing

classification tasks directly on OLAP data cubes has

become increasingly computationally expensive.

High-dimensional data presents significant

challenges, especially the curse of dimensionality,

where the feature space becomes so huge that data

points become sparse. This sparsity adversely affects

the performance of classification algorithms, leading

to longer computation times and potential overfitting.

Consequently, there is a need for efficient techniques

that can reduce computational costs while maintaining

high performance of classification.

https://orcid.org/0000-0002-7104-6415

https://orcid.org/0009-0007-3740-776X

This research has been made in the context of the

Excellence Chair in Big Data Management and Analytics

at University of Paris City, Paris, France.

The main challenge focused on in this research

regards the substantial computational load associated

with performing classification on high-dimensional

OLAP data cubes. Traditional classification methods

struggle with scalability in such areas due to the

extensive resources required for processing and the

potential degradation in accuracy caused by the high

number of dimensions. This issue is particularly acute

in real-time and mobile environments (e.g.,

(Mutersbaugh et al., 2023; Hussenet et al., 2024; Kim

et al., 2024)), where computational resources are

limited. Therefore, enhancing classification processes

to handle high-dimensional data efficiently is crucial

for enhancing the effectiveness of data analysis in

various applications.

Several research efforts have focused on

addressing the computational challenges associated

with high-dimensional data classification, particularly

in the context of large datasets (e.g., (Chen et al.,

2024; Shi et al., 2025)). Dimensionality reduction

techniques (e.g., (Sorzano et al., 2014)), such as

Principal Component Analysis (PCA) (Abdi &

Williams, 2010) and Feature Selection Algorithms

(e.g., (Molina et al., 2002; Song et al., 2024)), have

been widely employed to mitigate the curse of

dimensionality. For instance, (Cardone & Di Martino,

Cuzzocrea, A. and Hajian, M.

Towards Big OLAP Data Cube Classiﬁcation Methodologies: The ClassCube Framework.

DOI: 10.5220/0013448200003929

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 27th International Conference on Enterprise Information Systems (ICEIS 2025) - Volume 1, pages 351-356

ISBN: 978-989-758-749-8; ISSN: 2184-4992

351

2023) integrate PCA into a multidimensional F1-

transform classifier, effectively reducing

computational loads and improving classification

accuracy over traditional algorithms. Similarly, (Khan

& Nisha, 2024) develop a hybrid optimization-based

feature selection method to identify relevant feature

subsets, resulting in improved convergence speed and

classification performance on high-dimensional

datasets. Beyond using dimensionality reduction

methods, some studies have explored the integration

of these techniques with classification algorithms to

further enhance efficiency. (Tutsoy & Koç, 2024)

introduce deep self-supervised machine learning

models enriched with novel feature elimination and

selection strategies, effectively reducing

dimensionality and improving classification accuracy

for multidimensional health risk assessments.

Additionally, advanced data structuring methods have

been proposed to manage high-dimensional data more

effectively. (Ding et al., 2024) present an adaptive

granularity and dimension decoupling network for

multidimensional time series classification (e.g.,

(Elborough et al., 2024)), which extracts features at

various scales and decouples dimensions to prevent

dominant features from overshadowing others.

To tackle the aforementioned challenges, we

propose ClassCube, a novel methodology that

integrates multidimensional OLAP analysis (Gray et

al., 1997) and classification algorithms (Hassan et al.,

2018; Bohrer & Dorn, 2024) to effectively and

efficiently support big data analytics in real-life

scenarios. The key idea of ClassCube relies on

dimensionality reduction tools (e.g., (Sorzano et al.,

2014)). At a practical level, we leverage on so-called

big OLAP data cubes (Cuzzocrea, 2023) for big data

applications, and we address the issue of effectively

and efficiently classifying big multidimensional data

(Cuzzocrea et al., 2011) in Cloud environments (e.g.,

(Nodarakis et al., 2014)). With this goal in mind, we

propose the anatomy and main functionalities of

ClassCube, an innovative methodology for supporting

advanced big data analytics via intelligent

classification tools over big OLAP data cubes.

In our study, we focus on leveraging the logical

cuboid lattice (Gray et al., 1997), a hierarchical

structure that represents all possible aggregations of

the data across different combinations of dimensions.

Each cuboid in the lattice corresponds to a specific

aggregation level, offering a multi-resolution view of

the data. This structure leads the model to more

efficient data management and analysis by enabling

operations at different levels of granularity (e.g.,

(Wang & Cao, 2023; Tang et al., 2024)). However,

even with this hierarchical approach, performing

classification directly on the entire lattice remains

resource-intensive. It should be noted that the

selection process focuses on identifying specific

dimensions from the OLAP data cube to define the

cuboids of interest. This criterion can be guided by

user/application input or determined based on state-

of-the-art models (e.g., (Lin & Kuo, 2004; Talebi et

al., 2008)).

Our proposed methodology integrates

dimensionality reduction with hierarchical data cube

structuring to perform an efficient classification

process. Specifically, we extract the logical cuboid

lattice from the original OLAP data cube using

Principal Component Analysis to construct a new,

reduced-dimensionality data cube. PCA effectively

reduces the number of dimensions by projecting the

most significant features that contribute to data

variance, to a reduced feature space. Thus, mitigating

the curse of dimensionality. On the other hand, we

apply a dimension selection method to extract the

reduced-dimensionality data cubes, which then the

classification performance is compared with the one

resulting from PCA utilization. Thus, the reduced data

cube serves as the basis for our classification tasks.

We then perform classification using algorithms

such as Logistic Regression (LR) and Support Vector

Machines (SVM) on the cuboids of interest. The

reduced dimensionality substantially lowers

computational costs while aiming to preserve

classification accuracy.

The key contributions of this research are as

follows:

 first, we introduce an efficient dimensionality

reduction framework that employs a

hierarchical data cube structure to be used in

classification applications on high-dimensional

OLAP data cubes;

 second, our methodology applies classification

algorithms on the cuboids of interest from the

extracted lattice of cuboids;

 third, we establish a practical evaluation

methodology by comparing the reduced data

cubes (i.e., cuboids) from the lattice, providing

meaningful insights into the effectiveness of

our approach.

By addressing the computational inefficiencies

associated with high-dimensional data cube

classification, this research aims to enhance the

effectiveness of data analysis techniques in various

data-intensive applications, particularly those

operating under resource constraints. Our approach

provides a viable solution for contexts seeking to

leverage large, multidimensional datasets without

incurring prohibitive computational costs.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

352

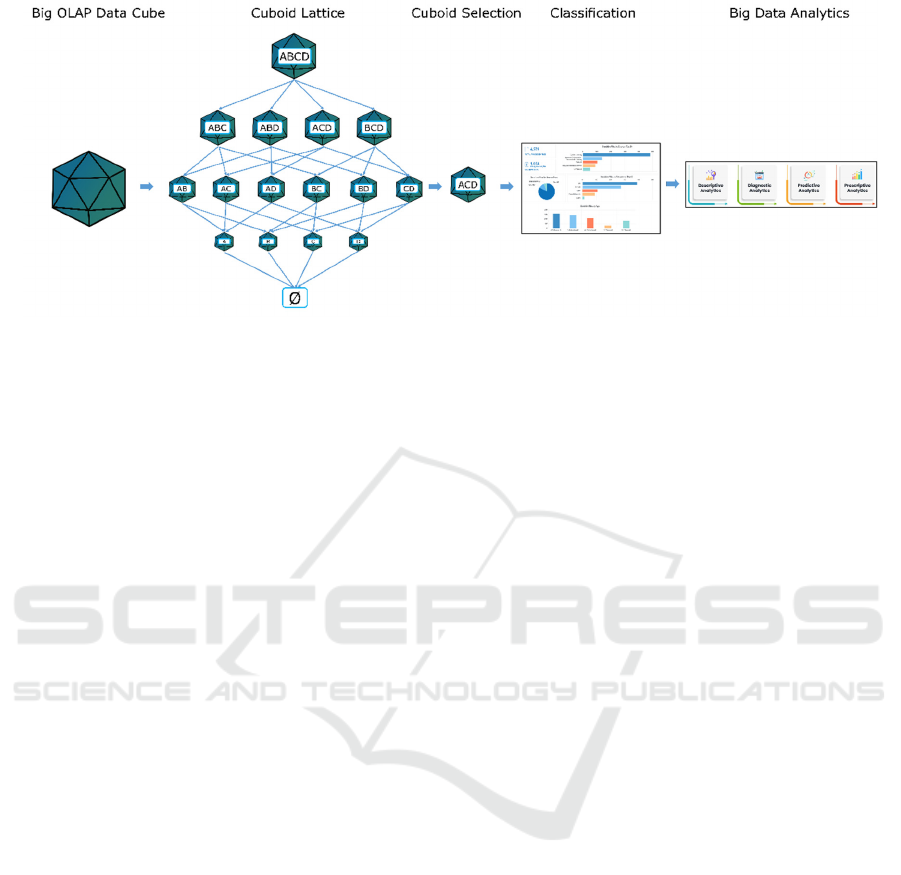
Figure 1: ClassCube Methodology.

2 CLASSCUBE: ANATOMY AND

MAIN FUNCTIONALITIES

In this Section, we present the ClassCube

methodology for classification of high-dimensional

OLAP data cubes by integrating dimensionality

reduction techniques with hierarchical data cube

structuring. Our approach aims to mitigate

computational costs on big OLAP data cube

classification while preserving the algorithm’s

performance.

2.1 Overview

Consider a big multidimensional OLAP data cube 𝑂

with 𝑁 dimensions, denoted as 𝐷={𝑑



,𝑑



,…,𝑑



This data cube contains aggregate data across all

possible combinations of these dimensions,

simplifying complex analytical queries such as

slicing, dicing, and drilling down into data. However,

performing classification directly on 𝑂 is

computationally expensive due to the high

dimensionality.

To address this challenge, we consider a logical

cuboid lattice 𝐿 from 𝑂. The lattice 𝐿 is a hierarchical

structure representing all possible aggregations of 𝑂

over different combinations of dimensions. Each

cuboid within 𝐿 corresponds to a specific level,

providing comprehensive multiple views of the data.

By working with cuboids of reduced dimensionality,

we aim to alleviate the computational costs associated

with high-dimensional data.

To provide more details, a cuboid 𝐶 is an

aggregation of the data over a subset 𝐷′ ⊆ 𝐷, where

𝐷′ contains a specified combination of dimensions.

The aggregation within a cuboid may involve

operations such as sum, average, or count, over the

dimensions in 𝐷′ . The hierarchical relationship

among cuboids is based on the principle of dimension

aggregation, where lower-dimensional cuboids are

derived by aggregating higher-dimensional ones over

one or more dimensions.

2.2 Construction of the Lattice Levels

The logical lattice 𝐿 is defined by hierarchically

structured cuboids at different levels as illustrated in

Fig. 1. This hierarchical structure enables analysis at

various levels of granularity, providing flexibility in

the selection of cuboids for classification tasks and

addressing challenges related to high dimensionality

and computational cost.

To achieve our goal of efficient classification, we

propose two approaches to obtain cuboids with the

same dimensionality:

 Dimension Selection;

 Principal Component Analysis.

In both approaches, a specific level 𝑘 (with

dimensionality 𝑘



) of the lattice 𝐿 is selected using

the selection criterion, which is obtained as

user/application input or determined as previously

described based on state-of-the-art models (e.g., (Lin

& Kuo, 2004; Talebi et al., 2008)). Then, a

classification algorithm is applied to each cuboid

𝐶



at level 𝑘.

2.2.1 Dimension Selection Approach

The dimension selection method involves selecting

specific subsets of dimensions from 𝐷 to create

reduced versions of 𝑂. For each level 𝑘 in the lattice

Towards Big OLAP Data Cube Classiﬁcation Methodologies: The ClassCube Framework

353

𝐿, where 𝑘 = 1,2,…,𝐾 and 𝐾≤𝑁, we define 𝑚



the number of dimensions at level 𝑘 (i.e., 𝑚



=𝑘



At each level 𝑘 , we select all possible

combinations of 𝑚



dimensions from 𝐷 . Each

combination 𝐷



⊂𝐷 defines a cuboid 𝐶



, where

𝑖 = 1,2,…,𝐼



, 𝐼













is the number of

combinations at level 𝑘. The cuboid 𝐶



is obtained

by aggregating 𝑂 over the dimensions included in

𝐷



Therefore, the set of cuboids at level 𝑘 is as

follows:

𝐿



{

𝐶



|𝐷



⊂𝐷,

𝐷



=𝑚



}

(1)

Each cuboid 𝐶



has dimensionality 𝑚



and

provides a view of the data over 𝑚



(= 𝑘



)

dimensions. By working with this lower-dimensional

cuboid, we reduce the computational complexity of

the classification task.

2.2.2 Cuboid Representation Using

Principal Component Analysis (PCA)

In our second approach, we use PCA to obtain a

reduced-dimensionality representation of the data

cube 𝑂 with the same dimensionality 𝑘



as in the

dimension selection approach. PCA is applied to 𝑂 to

reduce its dimensionality by transforming the original

data into a new set of orthogonal components that

capture the maximum variance.

We compute the covariance matrix Ʃ of 𝑂 and

solve for its eigenvalues and eigenvectors. The top 𝑘



eigenvectors corresponding to the largest eigenvalues

form the transformation matrix 𝑃. The reduced data

cube 𝐶



is obtained by projecting 𝑂 onto the new

feature space which provides 𝐶



as follows:

𝐶



=𝑂×𝑃 (2)

This projection results in a single reduced-

dimensionality representation, capturing the most

significant patterns in the data. By comparing the

classification performance using the cuboids from the

dimension selection approach and the PCA-reduced

data cube, we evaluate the effectiveness of our

methodology.

2.3 Classification Algorithms

We apply classification algorithms to the selected

cuboids 𝑆 to evaluate the effectiveness of our

dimensionality reduction approach. Specifically, we

use Logistic Regression and Support Vector

Machines, which are well-suited for handling

reduced-dimensionality data.

2.3.1 Logistic Regression

Logistic Regression models the probability 𝑃(𝑦 =

1∣𝑥) of a binary outcome using the logistic function

as follows:

𝑃

(

𝑦=1

∣

𝒙

)

1+𝑒

(







𝒙)

(3)

where 𝛽



is the intercept, 𝛽 is the coefficient vector,

and 𝑥is the feature vector from a cuboid 𝐶



. The

parameters 𝛽



and 𝛽 are estimated using Maximum

Likelihood Estimation (MLE). The likelihood

function for a set of observations

{

(

𝒙



,𝑦



)

}

,𝑖=

1,2,…,𝑛 is given by:

𝐿(𝛽



,𝛽)=𝑃(𝑦



|𝒙



)





[1−𝑃(𝑦



|𝒙



)]









(4)

Maximizing the likelihood function (or

equivalently, the log-likelihood) obtains estimates of

the parameters that best fit the observed data. The

optimization is typically performed using iterative

algorithms like Newton-Raphson or gradient descent.

To further prevent overfitting, regularization methods

can be imposed into the LR model. The common

regularization terms are as follows:

 L1 Regularization (Lasso Regression): Adds a

penalty equal to the absolute value of the

magnitude of coefficients. It performs feature

selection by shrinking some coefficients to

zero.

 L2 Regularization (Ridge Regression): Adds a

penalty equal to the square of the magnitude of

coefficients. It prevents large coefficients but

does not enforce sparsity.

The regularized cost function becomes as follows:

𝐽

(

𝛽



,𝛽

)

=−

𝑛

[𝑦



log𝑃

(

𝑦



𝑥



)





(

1−𝑦



)

log(1 −

𝑃

(

𝑦



𝑥



)

)] + 𝜆𝑅

(

𝛽

)

(5)

where 𝑅(𝛽) is the regularization term and 𝜆 is the

regularization parameter controlling the trade-off

between fitting the data and keeping the model

coefficients small.

2.3.2 Support Vector Machines

SVM are powerful supervised learning models used

for classification and regression tasks. They are

particularly effective in high-dimensional spaces and

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

354

are robust against overfitting, especially in cases

where the number of dimensions exceeds the number

of observations. SVMs are well-suited for our

methodology, which involves reduced-

dimensionality data cubes derived from high-

dimensional OLAP systems.

SVM algorithm seeks an optimal hyperplane that

maximally separates data points of different classes.

For linearly separable data, the objective is to

maximize the margin between the closest points

(support vectors) of the two classes. The optimization

problem is formulated as:

min

𝒘,

‖

𝒘

‖



𝑠.𝑡. 𝑦



(

𝒘



𝒙



+𝒃

)

≥ 1, ∀𝑖,

(6)

where 𝒘 is the normal vector to the hyperplane, 𝑏 is

the bias term, 𝒙



are the feature vectors, and 𝑦



∈

{−1,1} are the class labels. By solving this convex

optimization problem, SVM identifies the hyperplane

that not only separates the classes but does so with the

greatest possible margin, enhancing the model's

generalization capabilities.

Real-world data often cannot be perfectly

separated by a linear hyperplane. To address this,

SVM introduces the concept of kernel functions.

Kernel function projects the original feature space

into a higher-dimensional space where linear

separation is possible. Common kernels include:

 Linear Kernel: 𝐾𝒙



,𝒙



=𝒙



𝑻

𝒙



 Polynomial Kernel: 𝐾𝒙



,𝒙



=(𝛾𝒙



𝑻

𝒙



+𝑟)



 Radial Basis Function (RBF) Kernel:

𝐾𝒙



,𝒙



=𝑒𝑥𝑝(−𝛾𝒙



−𝒙





𝟐

)

Selecting appropriate hyperparameters is crucial

for SVM performance: (i) Regularization Parameter

𝐶: Determines the penalty for misclassification. A

large 𝐶 prioritizes classification accuracy on the

training data, potentially at the expense of

generalization. (ii) Kernel Parameters: Parameters

like 𝛾 in the RBF kernel or 𝑑 in the polynomial kernel

affect the flexibility of the decision boundary. (iii)

Cross-Validation: Techniques such as 𝑘-fold cross-

validation are used to systematically explore

combinations of hyperparameters to identify the

optimal model settings.

2.5 Integration with Big Data Analytics

Our methodology is designed to integrate with big

data analytics frameworks to handle large-scale

OLAP data cubes. By leveraging distributed

computing platforms such as Apache Hadoop or

Apache Spark, our method is enriched and capable of

applying classification and analytics more efficiently

and effectively than the traditional methods. This

integration enhances scalability and performance,

making the approach suitable for real-world

applications where data volume and complexity are

substantial.

3 CONCLUSIONS

In this paper, we propose ClassCube, an innovative

methodology for effective big OLAP data cube

classification via dimensionality reduction

techniques. Our proposed approach leverages logical

cuboid lattices to represent data at multiple

aggregation levels, which enables efficient selection

of dimensions and cuboids for classification tasks.

The actual study highlights the trade-off between

reduced computational overhead and maintained

classification accuracy. The use of Logistic

Regression and Support Vector Machines on reduced-

dimensional cuboids highlights that our approach

effectively preserves performance while significantly

reducing resource requirements.

Future work is mainly oriented through extending

our methodology with advanced machine learning

models to further enhance flexibility and scalability as

well as integrate emerging big data trends (e.g.,

(Cuzzocrea, 2006; Cuzzocrea, 2009; Cuzzocrea et al.,

2004; Cuzzocrea et al., 2007; Yu et al., 2012)).

ACKNOWLEDGEMENTS

This work was funded by the Next Generation EU -

Italian NRRP, Mission 4, Component 2, Investment

1.5 (Directorial Decree n. 2021/3277) - project

Tech4You n. ECS0000009.

REFERENCES

Abdi, H., & Williams, L.J. (2010). Principal Component

Analysis. Wiley Interdisciplinary Reviews:

Computational Statistics 2(4), pp. 433-459.

Bohrer, J.S., & Dorn, M. (2024). Enhancing Classification

with Hybrid Feature Selection: A Multi-Objective

Genetic Algorithm for High-Dimensional Data. Expert

Systems with Applications 255, art. 124518.

Cardone, B., & Di Martino, F. (2023). A Novel

Classification Algorithm Based on Multidimensional

F1 Fuzzy Transform and PCA Feature Extraction.

Algorithms 16(3), art. 128.

Towards Big OLAP Data Cube Classiﬁcation Methodologies: The ClassCube Framework

355

Cuzzocrea, A. (2006). Improving Range-SUM Query

Evaluation on Data Cubes via Polynomial

Approximation. Data and Knowledge Engineering

56(2), pp. 85-121.

Cuzzocrea, A. (2009). CAMS: OLAPing Multidimensional

Data Streams Efficiently. In: DaWaK 2009, 11th

International Conference on Data Warehousing and

Knowledge Discovery, pp. 48-62.

Cuzzocrea, A. (2023). Big OLAP Data Cube Compression

Algorithms in Column-Oriented Cloud/Edge Data

Infrastructures. In: BigMM 2023, 9th IEEE

International Conference on Multimedia Big Data, pp.

1-2.

Cuzzocrea, A., Furfaro, F., Mazzeo, G.M., & Saccà D.

(2004). A Grid Framework for Approximate Aggregate

Query Answering on Summarized Sensor Network

Readings. In: OTMW 2004, 2004 On the Move to

Meaningful Internet Systems International Workshops,

pp.144-153.

Cuzzocrea, A., Saccà, D., & Serafino, P. (2007). Semantics-

Aware Advanced OLAP Visualization of

Multidimensional Data Cubes. International Journal of

Data Warehousing and Mining 3(4), pp. 1-30.

Cuzzocrea, A., Song, I.Y., & Davis, K.C. (2011). Analytics

over Large-Scale Multidimensional Data: The Big Data

Revolution! In: DOLAP 2011, 14th ACM International

Workshop on Data Warehousing and OLAP, pp. 101-

104.

Chen, X., Ma, C., Zhao, C., & Luo, Y. (2024). UAV

Classification Based on Deep Learning Fusion of

Multidimensional UAV Micro-Doppler Image

Features. IEEE Geoscience and Remote Sensing Letters

21, pp. 1-5.

Ding, G., Geng, S., Jiao, Q., & Jiang, T. (2024). AGDM:

Adaptive Granularity and Dimension Decoupling for

Multidimensional Time Series Classification. In: ICIC

2024, 13th International Conference on Intelligent

Computing, pp. 405-416.

Elborough, L., Taylor, D., & Humphries, M. (2024). A

Novel Application of Shapley Values for Large

Multidimensional Time-Series Data: Applying

Explainable AI to a DNA Profile Classification Neural

Network. CoRR abs/2409.18156.

Gray, J., Chaudhuri, S., Bosworth, A., Layman, A.,

Reichart, D., Venkatrao, M., Pellow, F., & Pirahesh, H.

(1997). Data Cube: A Relational Aggregation Operator

Generalizing Group-by, Cross-Tab, and Sub Totals.

Data Mining and Knowledge Discovery 1(1), pp. 29-53.

Hassan, C.A.U., Khan, M.S., & Shah, M.A. (2018).

Comparison of Machine Learning Algorithms in Data

Classification. In: ICAC 2018, 24th IEEE International

Conference on Automation and Computing, pp. 1-6.

Hussenet, L., Boucetta, C., & Herbin, M. (2024). Spanning

Thread: A Multidimensional Classification Method for

Efficient Data Center Management. In: I4CS 2024, 24th

International Conference on Innovations for

Community Services, pp. 219-234.

Khan, A.A.R., & Nisha, S.S. (2024). Efficient Hybrid

Optimization-Based Feature Selection and

Classification on High Dimensional Dataset.

Multimedia Tools and Applications 83(20), pp. 58689-

58727.

Kim, Y., Camacho, D., & Choi, C. (2024). Real-Time

Multi-Class Classification of Respiratory Diseases

Through Dimensional Data Combinations. Cognitive

Computation 16(2), pp. 776-787.

Lin, W.Y., & Kuo, I.C. (2004). A Genetic Selection

Algorithm for OLAP Data Cubes. Knowledge and

Information Systems 6(1), pp. 83-102.

Molina, L.C., Belanche, L., & Nebot, A. (2002). Feature

Selection Algorithms: A Survey and Experimental

Evaluation. In: ICDM 2002, IEEE International

Conference on Data Mining, pp. 306-313.

Mutersbaugh, J., Lam, V., Linguraur, M.G., & Anwar, S.M.

(2023). Epileptic Seizure Classification using

Multidimensional EEG Spectrograms. In: SIPAIM

2023, 19th IEEE International Symposium on Medical

Information Processing and Analysis, pp. 1-4.

Nodarakis, N., Sioutas, S., Tsoumakos, D., Tzimas, G., &

Pitoura, E. (2014). Rapid AkNN Query Processing for

Fast Classification of Multidimensional Data in the

Cloud. CoRR abs/1402.7063.

Shi, Y., Ye, H.J., Man, D., Han, X., Zhan, D.C., & Jiang,

Y. (2025). Revisiting Multi-Dimensional Classification

from a Dimension-Wise Perspective. Frontiers of

Computer Science 19(1), art. 191304.

Song, C.H., Kim, J.S., Kim, J.M., & Pan, S.B. (2024).

Stress Classification Using ECGs Based on a Multi-

Dimensional Feature Fusion of LSTM and Xception.

IEEE Access 12, pp. 19077-19086.

Sorzano, C.O.S., Vargas, J., & Pascual-Montano, A.P.

(2014). A Survey of Dimensionality Reduction

Techniques. CoRR abs/1403.2877.

Talebi, Z.A., Chirkova, R., Fathi, Y., & Stallmann, M.F.

(2008). Exact and Inexact Methods for Selecting Views

and Indexes for OLAP Performance Improvement. In:

EDBT 2008, 11th ACM International Conference on

Extending Database Technology, pp. 311-322.

Tang, J., Chen, W., Wang, K., Zhang, Y., & Liang, D.

(2024). Probability-Based Label Enhancement for

Multi-Dimensional Classification. Information

Sciences 653, art. 119790.

Tutsoy, O., & Koç, G.G. (2024). Deep Self-Supervised

Machine Learning Algorithms with Novel Feature

Elimination and Selection Approaches for Blood Test-

Based Multi-Dimensional Health Risks Classification.

BMC Bioinformatics 25(1), art. 103.

Wang, S., & Cao, G. (2023). Multiclass Classification for

Multidimensional Functional Data Through Deep

Neural Networks. CoRR abs/2305.13349.

Yu, B., Cuzzocrea, A., Jeong, D.H., & Maydebura, S.

(2012). On Managing Very Large Sensor-Network

Data Using Bigtable. In: CCGrid 2012, 12th

IEEE/ACM International Symposium on Cluster, Cloud

and Grid Computing, pp. 918-922.

ICEIS 2025 - 27th International Conference on Enterprise Information Systems

356