Clustering-Based Pattern Prediction Framework

for Air Pollution Prediction

Athiruj Poositaporn

1,2

and Hanmin Jung

1,2,*

University of Science and Technology, 217, Gajeong-ro, Yuseong-gu, Daejeon, Gyeonggi-do, Republic of Korea

Korea Institute of Science and Technology Information, 245, Daehak-ro, Yuseong-gu, Daejeon, Republic of Korea

Keywords: Internet of Things, Pattern Prediction, Prediction Framework, Pattern Analysis, K-means Clustering.

Abstract: Accurately predicting patterns from large and complex datasets remains a significant challenge, particularly

in environments where real-time predictions are crucial. Despite advancements in predictive modeling, there

remains a gap in effectively integrating clustering techniques with advanced similarity metrics to enhance

prediction accuracy. This research introduces a clustering-based pattern prediction framework integrating K-

means with our Overall Difference with Crossover Penalty (OD with CP) similarity metric to predict data

patterns. In the experiment, we demonstrated its application in air pollution pattern prediction by comparing

15 different model-cluster combinations. We employed five predictive models: Euclidean Distance, Markov

Chain, XGBoost, Random Forest, and LSTM to predict the next day's pollution pattern across three cluster

sizes (K = 10, 20, and 30). Our aim was to address the limitation of traditional clustering methods in pattern

prediction by evaluating the performance of each model-cluster combination to determine the most accurate

predictions. The results showed that our framework identified the most accurate model-cluster combination.

Therefore, the study highlighted the generalizability of our framework and indicated its adaptability in pattern

prediction. In the future, we aim to apply our framework to a Large Language Model (LLM) combined with

Retrieval Augmented Generation (RAG) to enhance in-depth result interpretation. Furthermore, we intend to

expand the study to include client engagement strategy to further validate the effectiveness of our study in

real-world applications.

1 INTRODUCTION

The Internet of Things (IoT) is a revolutionary

network of interconnected devices with sensors and

software integrated in, enabling continuous data

exchange and driving innovation across industries.

However, the vast data volumes generated by IoT

systems require advanced techniques to extract and

predict meaningful patterns within complex datasets.

Pattern analysis plays a critical role in addressing this

challenge. It offers systematic approaches to identify

relationships, trends, and structures within diverse

sources of information (Han et al., 2012). Pattern

analysis has an extensive range of applications,

including data mining, image processing, signal

analysis, bioinformatics, and machine learning

(Wang et al., 2022; M. Wang et al., 2021; Li et al.,

2022). The ability to detect meaningful patterns

within complex and massive datasets is a crucial skill

Corresponding author

in today's data-driven world, driving innovation and

facilitating knowledge discovery across scientific and

industrial sectors (Qiu et al., 2016).

Many previous studies have successfully utilized

pattern analysis approaches to identify recurring

structures in data using machine learning techniques

(Zeng et al., 2022; Feng et al., 2021).

For instance, some studies in environmental

science aim to find fluctuations and trends in air

pollution levels over time and predict their patterns

using historical data combined with real-time

environmental variables (Bhatti et al., 2021; Ma &

Liu, 2021). However, the use of clustering techniques

like K-means has been limited in prediction tasks.

Using K-means clustering can help identify patterns

in complex data and better encapsulate the main

characteristics of each cluster (Kobylin & Lyashenko,

2017). One of the key components of K-means

clustering is the calculation of centroids, which

428

Poositaporn, A. and Jung, H.

Clustering-Based Pattern Prediction Framework for Air Pollution Prediction.

DOI: 10.5220/0013474300003944

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Internet of Things, Big Data and Security (IoTBDS 2025), pages 428-435

ISBN: 978-989-758-750-4; ISSN: 2184-4976

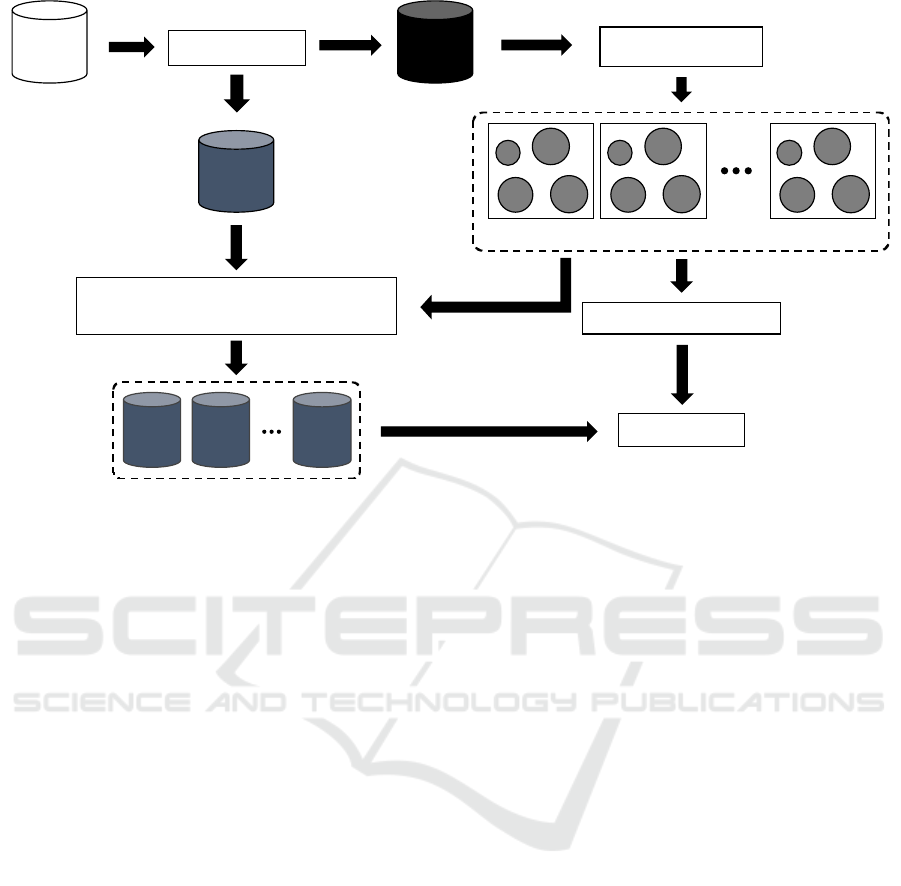
Figure 1: Process pipeline of clustering-based pattern prediction framework.

represent the average of every data point in a cluster

(Aamer et al., 2020). These centroids are then used to

assign new data points to the closest cluster according

to a predefined similarity metric. Finding the closest

centroid to new data can provide a quick and effective

way for pattern prediction based on previously

observed patterns. This approach can be highly

beneficial in real-time systems, where rapid

predictions are crucial. Therefore, the clustering

technique could improve the utility and

responsiveness of predictive models in various

applications.

Our previous research on integrating our Overall

Difference with Crossover Penalty (OD with CP) as a

similarity metric for K-means clustering prediction

demonstrated that the integrated approach identified

distinct clusters with the optimal number of clusters

and established the basis for further data analysis and

interpretation, allowing for a more extensive

understanding of air pollution patterns and possible

causes (Poositaporn et al., 2023, 2024).

We aim to address this gap by introducing a

clustering-based pattern prediction framework. Our

proposed framework combines the strengths of

K-means clustering and our similarity algorithm to

accurately predict patterns in any complex data. The

framework processes an input dataset by

preprocessing it into a vector format. The data is then

split into training and testing subsets before being

passed into the K-means clustering algorithm. Testing

data points are labeled by assigning each to the most

similar cluster centroid. The prediction model's

accuracy is evaluated and trained using these labeled

data points. This approach allows for the efficient

prediction of patterns in diverse datasets, making it a

versatile tool for various domains. In this study, we

demonstrate the framework on air pollution dataset to

predict the next day's air pollution pattern to

determine the optimal combination numbers of

clusters and predictive models.

2 CLUSTERING-BASED

PATTERN PREDICTION

FRAMEWORK

Figure 1 shows the process pipeline for our proposed

framework consisting of five key steps: data

preparation, K-means clustering, labeling testing

data, pattern prediction, and evaluation. The

description of each step is shown below:

1) Data preparation

This initial step involves cleaning the raw dataset to

remove any inconsistencies or irrelevant information.

The data is then normalized to ensure that it is on a

consistent scale and transformed into vector format.

Finally, the data is split into training and testing

subsets.

Training

Data

K-Means Clustering

Pattern Prediction

Evaluation

Dataset

Data Preparation

Testing

Data

Clustered Data K

Testing

data

Testing

data

Testing

data

Labeling Testing Data

(Assign the Most Similar Centroid as Label)

Clustering-Based Pattern Prediction Framework for Air Pollution Prediction

429

2) K-means clustering

The training data is given to the K-means clustering

algorithm, which employs our OD with CP similarity

metric to divide the data into clusters. The elbow

approach is used to find the ideal number of clusters

(K). The within-cluster sum of squares (WCSS) is

plotted against the number of clusters in order to

determine the point at which the rate of reduction

rapidly slows down (Marutho et al., 2018).

Additionally, we use the silhouette score to validate

the consistency within clusters, with a higher score

indicating better-defined clusters.

3) Labeling testing data

Each data point in the testing set is assigned to the

cluster with the nearest centroid. This testing data can

then be used to evaluate the performance of the

predictive model.

4) Pattern prediction

The framework uses the cluster centroids in the

predefined predictive model to predict future patterns.

This requires interpreting the characteristics of each

cluster to forecast the behavior of new data points.

5) Evaluation

The final stage involves evaluating the accuracy and

effectiveness of the pattern predictions. Various

metrics, including root mean squared error (RMSE),

mean reciprocal rank (MRR), and other relevant

evaluation criteria, can be applied to evaluate the

performance of the predictions. This evaluation helps

refine the model and improve future predictions,

ensuring the framework's robustness and reliability in

different applications.

3 AIR POLLUTION PATTERN

PREDICTION

In this section, we demonstrate the application of our

framework for predicting air pollution patterns. The

process flow in Figure 2 details the adapted

framework for a comparative analysis study on air

pollution pattern prediction that combines clustering

and machine learning to predict air pollution for the

next day.

We begin by dividing the dataset into training and

testing subsets. The training set undergoes K-means

clustering to create three distinct datasets for K = 10,

20, and 30 clusters. For the testing set, we classify

each data point into a cluster by identifying the most

similar centroid and labeling it with the

corresponding cluster label. We then train five

different predictive models: Euclidean Distance,

Markov Chain, XGBoost, Random Forest, and

LSTM, on each of these clustered datasets. Therefore,

our experiment will consist of 15 different model-

cluster combinations. Then, we evaluate the models

using the MRR metric and compare the prediction

performance of each model. The details of each stage

are shown in the following:

3.1 Data Preparation

The study uses a dataset of Seoul air pollution

measurements from 25 stations collected between

2017 and 2021. The data consist of four features: date,

daily concentrations of six air pollutants (CO, SO

, O

, PM

, and PM

2.5

), air pollutant information,

and 44,751 recordings of air quality monitoring

station information. In this study, we focus on five air

pollutants: CO, SO

, NO

, O

, PM

, and PM

2.5

In the first stage, we select six features from the

dataset (date and five air pollutants). Then, we

preprocess the data by normalizing the concentration

measures using Z-score, concatenating all pollutants

into vector form, and splitting the dataset into 35,865

records for training and 8,886 records for testing

datasets.

3.2 K-means Clustering

In the clustering stage, we employ the K-means

algorithm to form three separate clusters: K = 10, 20,

and 30. Initially, the algorithm generates random

centroids and categorizes data points according to

their proximity. The refinement of these groupings

involves recalculating centroids and reallocating data

points to the newly established centroids (Marutho et

al., 2018). This iterative adjustment facilitates the

formation of clusters that are both homogeneous

within and clearly separated from each other (Ikotun

et al., 2023). Our choice of K = 30 is based on our

prior study in (Poositaporn et al., 2024), which

showed that 30 is the optimal cluster number. In this

experiment, we aim to find the optimal number of K

that encapsulate the characteristics of air pollution

patterns. Therefore, we introduce K values of 10 and

20 to test if a smaller number of clusters can still

accurately predict air pollution patterns.

Furthermore, we modify the proximity calculation

by integrating the Overall Difference with Crossover

Penalty (OD with CP). This method measures the

slope difference between two patterns and introduces

a penalty to the similarity score, as shown in the

following equation:

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

430

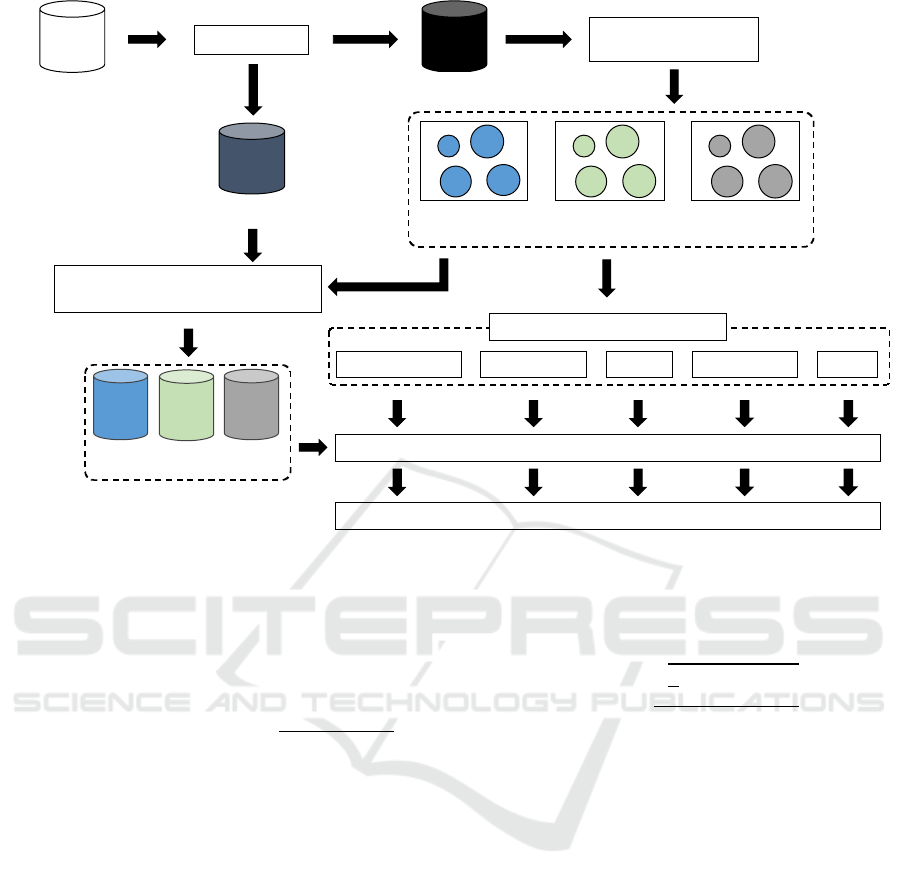
Figure 2: Process pipeline of air pollution pattern prediction.

𝑂𝐷𝐸



,𝐸



=𝐸



,𝐸



−𝐸



,𝐸









𝐶𝑃𝐸



,𝐸



=

1, 𝑖𝑓 𝐸



>𝐸



 𝑎𝑛𝑑 𝐸



<𝐸





1, 𝑖𝑓𝐸



<𝐸



 𝑎𝑛𝑑 𝐸



>𝐸





0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒





𝑂𝐷 𝑤𝑖𝑡ℎ 𝐶𝑃𝐸



,𝐸



=𝑂𝐷𝐸



,𝐸





1+𝐶𝑃𝐸



,𝐸





𝑛+1



(

)

where OD(E

) is a slope similarity function

considering the difference between air pollution

patterns. E

p,q

is an air pollution pattern of n

dimensions. n is the number of pattern dimensions.

CP(E

) is a similarity penalty function. A lower

OD with CP value shows greater similarity between

the two patterns, while zero indicates that the two

patterns are identical.

3.3 Labeling Testing Data

In the next stage, we process the testing dataset by

comparing each data point to the most similar

centroids using OD with CP as the similarity metric.

As a result, we generate three distinct sets of labeled

testing data corresponding to the three sets of clusters.

To ensure accurate labeling of the testing data, we

further validate the accuracy of the assigned labels by

calculating the max-min normalized root mean square

error (NRMSE) between the actual air pollution

patterns and the obtained centroids. The NRMSE is

computed using the formula:

𝑁𝑅𝑀𝑆𝐸=



𝑑

(𝑞



−𝑝



)







𝑞



−𝑞



(

)

where d is the number of instances in the dataset. q

the real air pollution pattern vector. p

is the

predicted cluster's centroid vector. q

max/min

is the

maximum and minimum air pollution vector. A

value close to 0 indicates the minimal error, whereas

a value close to 1 suggests the maximal error.

We then use these labeled sets in the evaluation

stage to compare and analyze the performance of

each prediction model across different clusters.

3.4 Air Pollution Prediction

This stage aims to construct and predict the air

pollution level for the next day. For instance, if T

represents today's air pollution pattern, then T+1

would denote tomorrow's pattern. Similarly, if Ct is

the cluster linked to T, then Ct+1 would be the

cluster corresponding to T+1. In practice, the

predictive models use T to predict the cluster Ct+1

for T+1. These models are trained on clustered

training data with the objective of identifying the

Training

Data

Clustered Data

K = 10

Markov Chain XGBoost

Data from 2017 to 2020:

35,865 records

Data from 2021:

8,886 records

Testing

Data

Labeling Testing Data

(Assign the Most Similar Centroid as Label)

Clustered Data

K = 20

Clustered Data

K = 30

Testing

data

K = 10

Testing

data

K = 20

Testing

data

K = 30

8,886

records

8,886

records

8,886

records

Random Forest LSTM

K-Means Clustering:

K = 10, 20, 30

Euclidean Distance

Air Pollution Pattern Prediction

Evaluation (MRR)

Predictive Models Comparison

Dataset

Data Preparation

Data from 2017 - 2021:

44,751 records

Clustering-Based Pattern Prediction Framework for Air Pollution Prediction

431

cluster that best represents the expected future

pollution pattern. For this purpose, we have

employed five well-established machine learning

algorithms: Markov Chain, XGBoost, Random

Forest, LSTM, and Euclidean Distance, as their

proven effectiveness in capturing temporal

dependencies, handling non-linear relationships,

and identifying patterns within structured pollution

data.

1) Euclidean distance

Euclidean distance is a straightforward and

interpretable model that calculates the linear distance

of two points in a multidimensional space (Weller-

Fahy et al., 2015). Our aim in using this method is to

establish a baseline benchmark for the accuracy and

performance of the other prediction models. This

method involves calculating the distance between the

centroid of each cluster and a target data point.

2) Markov chain

This method considers the transitions between

different air pollution clusters over time. It assumes

that the future air pollution pattern depends only on

the current pattern and not on the past patterns. The

Markov chain model calculates the transition

probabilities between different clusters based on

historical data and uses these probabilities to predict

the centroid of the next day's pollution pattern

(Besenczi et al., 2021).

The centroid with the highest probability

represents the expected pollution pattern, as it

indicates the highest probability cluster that the target

data point will belong to in the next time step.

3) XGBOOST

One machine learning technique that is particularly

helpful for regression and classification problems is

called XGBoost, or eXtreme Gradient Boosting

(Chen & Guestrin, 2016). XGBoost builds a strong

predictive model by iteratively combining the outputs

of multiple weak learners. The algorithm starts with

an initial simple model and iteratively improves its

performance by adding new trees that correct the

errors of the existing ensemble. Each tree tries to

minimize the residual errors of the combined model

using a gradient descent optimization technique in

every iteration.

4) Random forest

Random forest is a robust machine learning algorithm

that performs by developing numbers of decision

trees at training time and providing the result for the

classification task or regression task (Biau & Scornet,

2016). Each tree works on a random subset of data to

provide diversity among the trees and results in a

model with high robustness against overfitting. This

method involves creating trees using different

portions of the dataset (bootstrapping), encouraging

the model's generalization. The random selection of

features for splitting within the trees also ensures that

the model's bias might partially increase. However,

this is balanced by a significant drop in variance

throughout the ensemble of trees.

5) LONG SHORT-TERM MEMORY (LSTM)

LSTM networks are a type of recurrent neural

network developed to address the limitation on

learning long-term dependencies in sequence data

(Hochreiter & Schmidhuber, 1997). LSTM uses a

gating mechanism that includes input, forget, and

output gates, allowing the network to selectively

maintain or forget information over time. This

capability makes LSTM highly effective for

applications that require a complex understanding of

temporal sequences, such as time series data in air

pollution prediction. Additionally, it helps prevent the

problems of vanishing and exploding gradients,

which makes it a reliable option for modeling

complex sequences.

In this study, we perform a range of

hyperparameter tuning using grid search to optimize

the XGBoost, Random Forest, and LSTM models.

Furthermore, the performance evaluation of each

model involves using the Mean Reciprocal Rank

(MRR) to determine the most effective approach for

air pollution prediction.

3.5 Models Evaluation and

Comparison

The MRR is a matric used to evaluate the

effectiveness of algorithms that predict rankings or

sequences (Brama, 2023). It calculates the average

of the reciprocal ranks of the first correct answer

across several instances, highlighting the model's

effectiveness at identifying the top possible

outcomes. Using MRR as a metric is similar to the

approach taken to predict weather forecasts, where

it offers a spectrum of likely conditions (Bi et al.,

2023). The calculation of MRR is shown as follows:

𝑀𝑅𝑅=

𝑄



𝑟𝑎𝑛𝑘







(

)

where Q is the total number of predictions. rank

the position of the first relevant answer within the

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

432

list of predictions for the i-th predicted pollution

pattern.

The final stage involves comparing the MRR

results of each algorithm for each K value to identify

the most accurate prediction model.

4 EXPERIMENTAL RESULTS

AND DISCUSSION

This section discusses the experimental results from

our adapted framework. The experiment initially

clustered the air pollution data into three groups using

K-means clustering with K values of 10, 20, and 30.

After that, we evaluated the effectiveness of these

clusters through their silhouette scores, which

measure the cohesion and separation within the

clusters.

The results of these clusters allowed us to train

five predictive models (Euclidean Distance, Markov

Chain, XGBoost, Random Forest, and LSTM) to

predict air pollution patterns. Lastly, we evaluate and

compare each model's performance using the MRR

metric and compare the results to determine the most

accurate model.

4.1 Experimental Results for K-means

The NRMSE results in Table 1 indicated that the

assigned labels were highly accurate and showed

minimal error between the actual and predicted air

pollution patterns. This validation process ensures

that the clustering algorithm accurately captures the

patterns in the data.

Moreover, we employed the silhouette score

metric to determine the performance and quality of

these clusters. Where 1 indicates a perfect fit and -1

indicates a poor match between the data points and

their corresponding cluster. For consistency of the

similarity metric, we used OD with CP for

calculating the silhouette scores.

Table 1: Evaluation results of K-means of each cluster.

Matric

Number of clusters

10 20 30

NRMSE 0.0393 0.0297 0.0262

Silhouette Scores 0.5980 0.6614 0.6871

Therefore, the silhouette score in Table 1

confirms strong separation and cohesion within the

clusters. The scores of 0.5980, 0.6614, and 0.6871

for cluster 10, 20, and 30 indicated that the clusters

formed by the OD with CP similarity metric were

sufficiently accurate and reliable for training our

predictive models.

4.2 Experimental Results for Predictive

Models

This study conducted an experimental analysis of

five predictive models: Euclidean Distance, Markov

Chain, XGBoost, Random Forest, and LSTM. These

models were trained on the clustered air pollution

data with the objective of predicting future pollution

patterns. Furthermore, we performed fine-tuning on

XGBoost, Random Forest, and LSTM to optimize

their performance across different cluster sizes

Table 2: Tuned hyperparameters of predictive models for

each cluster.

Predictive

Models

Hyper

parameters

Tuned Values

for K Cluster

10 20 30

XGBoost n_estimators 150 100 100

colsample_bytree 1 1 1

eta 0.1 0.1 0.1

max_depth 4 4 4

scale_pos_weight 1 1 1

subsample 0.5 0.5 0.5

Random

n_estimators

100

150

100

Forest bootstrap TRUE TRUE TRUE

max_depth 4 4 4

max_features auto auto auto

min_samples_leaf 1 1 4

min_samples_split 2 2 2

LSTM

epochs

batch_size 32 32 32

lstm_units 50 50 50

learning_rate 0.005 0.005 0.005

early_stopping 5 5 5

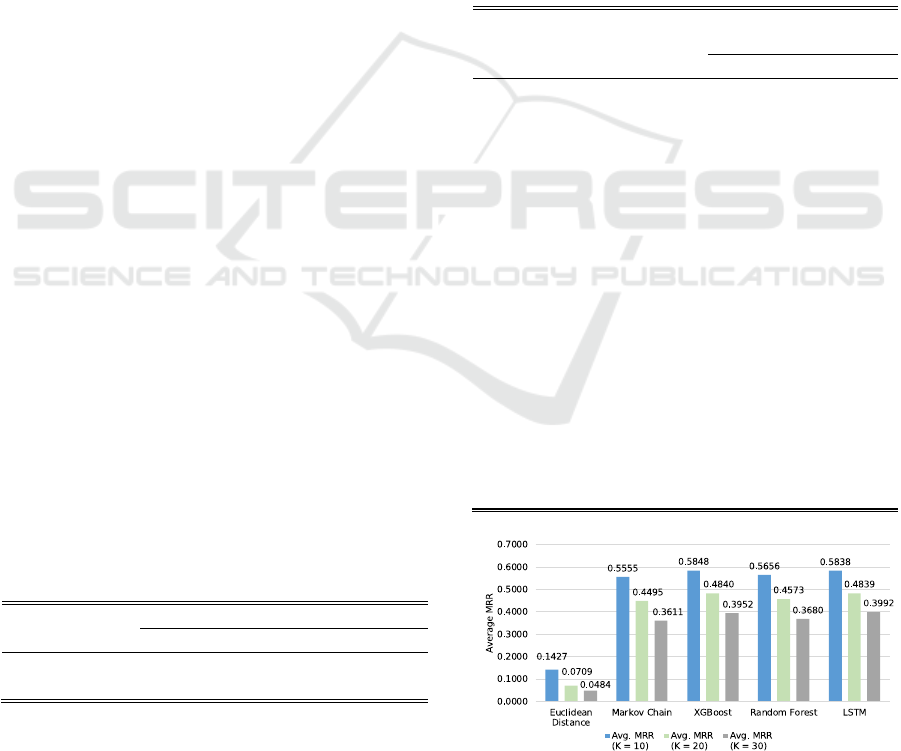
Figure 3: Average MRR of all predictive models for each

cluster.

Clustering-Based Pattern Prediction Framework for Air Pollution Prediction

433

(K = 10, 20, and 30). This process involved

adjusting specific hyperparameters to optimize each

model effectively according to the characteristics of

the clustered data. The fine-tuned results are shown

in Table 2. In the following section, we discuss the

detailed results of each model for each cluster size

based on the average MRR score.

Figure 3 revealed the average MRR scores that

reflect the effectiveness of all 15 model-cluster

combinations. For K = 10, the XGBoost and LSTM

models achieved higher predictive performance with

average MRRs of 0.5848 and 0.5838. This indicated

the average prediction results were generally on the

second rank out of 10 possible options. However, the

Euclidean Distance model performed poorly with an

average MRR of 0.1427, indicating that its

predictions were often lower in the ranking. This

suggested that Euclidean Distance was not suitable

for our prediction tasks.

The average MRR scores across all models were

noticeably declining when the cluster size increased

to K = 20 and 30. This phenomenon could be

attributed to the greater complexity of a larger

number of clusters. This highlights the importance of

finding the optimal balance between cluster size and

predictive performance when utilizing different

models for prediction tasks.

This experiment confirms that using our

clustering-based pattern prediction framework can

effectively capture the underlying structure of the

data and make reasonable predictions. Additionally,

the adapted framework highlights the importance of

selecting an appropriate cluster size to achieve

optimal results in pattern prediction tasks.

5 CONCLUSION

This study proposed a clustering-based pattern

prediction framework that integrates our Overall

Difference with Crossover Penalty (OD with CP) as

a similarity metric for K-means clustering to

accurately predict complex data patterns. In the

experiment, we demonstrated an application of our

framework by adapting it for a study of comparative

analysis on air pollution pattern prediction. We

employed five different predictive models

(Euclidean Distance, Markov Chain, XGBoost,

Random Forest, and LSTM) to predict the next day's

pollution pattern. These models were evaluated

across three cluster sizes (K = 10, 20, and 30) to

assess their performance. The aim of the experiment

was to determine the most effective combination for

achieving accurate predictions.

The results showed that K-means clustering with

10 clusters combined with XGBoost and LSTM

yielded better performance in achieving the highest

prediction rankings compared to other models. On

the other hand, increasing the number of clusters to

20 and 30 resulted in a noticeable decline in

performance across all models. This suggested that

using 10 clusters was sufficient to capture the

characteristics of the air pollution pattern and

provided optimal prediction accuracy.

Therefore, the experiment confirms the

generalizability and cross-domain applicability of

our framework. This also demonstrates its

robustness and adaptability in predicting complex

data patterns.

In future work, we aim to use our framework to

delve into a deeper understanding by using a Large

Language Model (LLM) combined with Retrieval

Augmented Generation (RAG) to enhance in-depth

result interpretation. Furthermore, we intend to

expand the study to include client engagement

strategy to further validate the effectiveness of our

study in real-world applications.

ACKNOWLEDGEMENTS

This work was supported by UST Young Scientist+

Research Program 2024 through the University of

Science and Technology. (No. 2024YS12)

REFERENCES

Han, J., Kamber, M., & Pei, J. (2012). Data mining:

Concepts and techniques (3rd ed.). Morgan Kaufmann

Publishers.

Wang, Y., Zhang, Y., Wang, L., Hu, Y., & Yin, B. (2022).

Urban traffic pattern analysis and applications based on

spatiotemporal non-negative matrix factorization. IEEE

Transactions on Intelligent Transportation Systems,

23(8), 12752–12765.

Wang, M., Shao, W., Hao, X., Shen, L., & Zhang, D.

(2021). Identify consistent cross-modality imaging

genetic patterns via discriminant sparse canonical

correlation analysis. IEEE/ACM Transactions on

Computational Biology and Bioinformatics, 18(4),

1549–1561.

Li, W., Zhao, Y., Ding, X., Wu, L., & Nie, Z. (2022). A

wideband pattern-reconfigurable loop antenna designed

by using characteristic mode analysis. IEEE Antennas

and Wireless Propagation Letters, 21(2), 396–400.

IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security

434

Qiu, J., Wu, Q., Ding, G., Xu, Y., & Feng, S. (2016). A

survey of machine learning for big data processing.

EURASIP Journal on Advances in Signal Processing,

2016(1), 67.

Zeng, Z., Li, Y., Li, Y., & Luo, Y. (2022). Statistical and

machine learning methods for spatially resolved

transcriptomics data analysis. Genome Biology, 23(1),

1–23.

Feng, S., Zuo, C., Hu, Y., Li, Y., & Chen, Q. (2021). Deep-

learning-based fringe-pattern analysis with uncertainty

estimation. Optica, 8(12), 1507–1510.

Bhatti, U. A., Yan, Y., Zhou, M., Ali, S., Hussain, A.,

Qingsong, H., Yu, Z., & Yuan, L. (2021). Time series

analysis and forecasting of air pollution particulate

matter (PM2.5): An SARIMA and factor analysis

approach. IEEE Access, 9, 41019–41031.

Ma, F., & Liu, Q. (2021). Fuzzy pattern recognition for

atmospheric quality in the original location of Capital

Iron and Steel Company. 2011 Eighth International

Conference on Fuzzy Systems and Knowledge

Discovery (FSKD), 429–432.

Kobylin, O., & Lyashenko, V. (2017). Time series

clustering based on the k-means algorithm. Journal La

Multiapp, 894–903.

Aamer, Y., Benkaouz, Y., Ouzzif, M., Bouragba, K. (2020)

Initial centroid selection method for an enhanced

kmeans clustering algorithm, Ubiquitous Networking:

5th International Symposium, 182–190.

Poositaporn, A., Jung, H., & Lee, D. (2024). Air pollution

pattern analysis combined vector slope and k-means

clustering. In Proceedings of the International

Conference on Future Information & Communication

Engineering.

Poositaporn, A., Jung, H., Park, J., & Onuean, A. (2023).

Similarity measuring for air pollution patterns based on

vector slope. In Proceedings of the Korean Society for

Internet Information Spring Conference.

Poositaporn, A., Jung, H., Park, J., & Onuean, A. (2023).

Towards multiple window framework for pattern

analysis. In Proceedings of the Korea Computer

Congress.

Poositaporn, A., Jung, H., Park, J., & Onuean, A. (2023).

Analysis of the influence of observation duration and

individual air pollutants on air quality prediction. In

Proceedings of the Korea Artificial Intelligence

Conference.

Marutho, D., Handaka, S. H., & Muljono, E. W. (2018). The

determination of cluster number at K-mean using elbow

method and purity evaluation on headline news. In 2018

International Seminar on Application for Technology of

Information and Communication, 533-538.

Ikotun, A. M., Ezugwu, A. E., Abualigah, L., Abuhaija, B.,

& Heming, J. (2023). K-means clustering algorithms: A

comprehensive review, variants analysis, and advances

in the era of big data. Information Sciences, 622, 178–

210.

Weller-Fahy, D. J., Borghetti, B. J., & Sodemann, A. A.

(2015). A survey of distance and similarity measures

used within network intrusion anomaly detection. IEEE

Communications Surveys & Tutorials, 17(1), 70–91.

Besenczi, R., Bátfai, N., Jeszenszky, P., Major, R., Monori,

F., & Ispány, M. (2021). Large-scale simulation of

traffic flow using Markov model. PLoS ONE, 16(2).

Chen, T., & Guestrin, C. (2016). XGBoost: A scalable tree

boosting system. In Proceedings of the 22nd ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining, 785–794.

Biau, G., & Scornet, E. (2016). A random forest guided

tour. TEST, 25(2), 197–227.

Hochreiter, S., & Schmidhuber, J. (1997). Long short-term

memory. Neural Computation, 9(8), 1735–1780.

Brama, H. (2023). Evaluation of neural networks defenses

and attacks using NDCG and reciprocal rank metrics.

International Journal of Information Security, 22(2),

525–540.

Bi, K., Xie, L., Zhang, H., Chen, X., Gu, X., & Tian, Q.

(2023). Accurate medium-range global weather

forecasting with 3D neural networks. Nature,

619(7970), 533–538.

Clustering-Based Pattern Prediction Framework for Air Pollution Prediction

435