EV-Connect: Energy Efficient & Incentive Cost Based Model for Range
Anxious EVs with Multi-Hop Socially Assisted V2V Charging
Srishti Sharma and Rahul Thakur
Computer Science and Engineering, Indian Institute of Technology Roorkee, India
Keywords:
Electric Vehicle (EV), Vehicle-to-Vehicle (V2V), Social Internet of Vehicles (SIoV), Incentive Cost, Bipartite
Matching.
Abstract:
With an increasing demand for a sustainable environment, there has been a rapid shift from internal combustion
engines (ICEs) to battery-powered engines (BPEs), which are installed in electric vehicles (EVs). With the
increasing need and demand for electric vehicles (EVs), the need for charging stations (CS) is also increasing.
However, the paradigm shift is slow regarding CSs because of their high installation costs. Thus, there is still
the non-ubiquity of CSs in cities, highways, and remote areas, which causes EV users to experience range
anxiety. In this context, vehicle-to-vehicle (V2V) charging could be a promising solution recently gaining
prominence. In this paper, we have proposed the incentive-based socially connected V2V charging model for
EVs where the excess charge of EVs acts as an alternate charging option for other EVs. We have used the
maximum bipartite matching algorithm to map the EVs experiencing range anxiety with available CSs and
other EVs with surplus charge. The results of our model have shown the trend that the number of EV users
who were experiencing range anxiety is less than the only CS-dependent users. Also, the trend of results
indicates that there could be a significant reduction of load on the power grid in that particular area, especially
during peak hours.
1 INTRODUCTION
In recent years, there has been continuous demand
to lower the emission of greenhouse gases (GHG),
which has raised the widespread adoption of EVs.
Gasoline-powered vehicles alone are responsible for
40% of CO
2
emissions and 70% of the other GHG
gases (Frade et al., 2011). In contrast to them, EVs
are more environmentally friendly, energy-efficient,
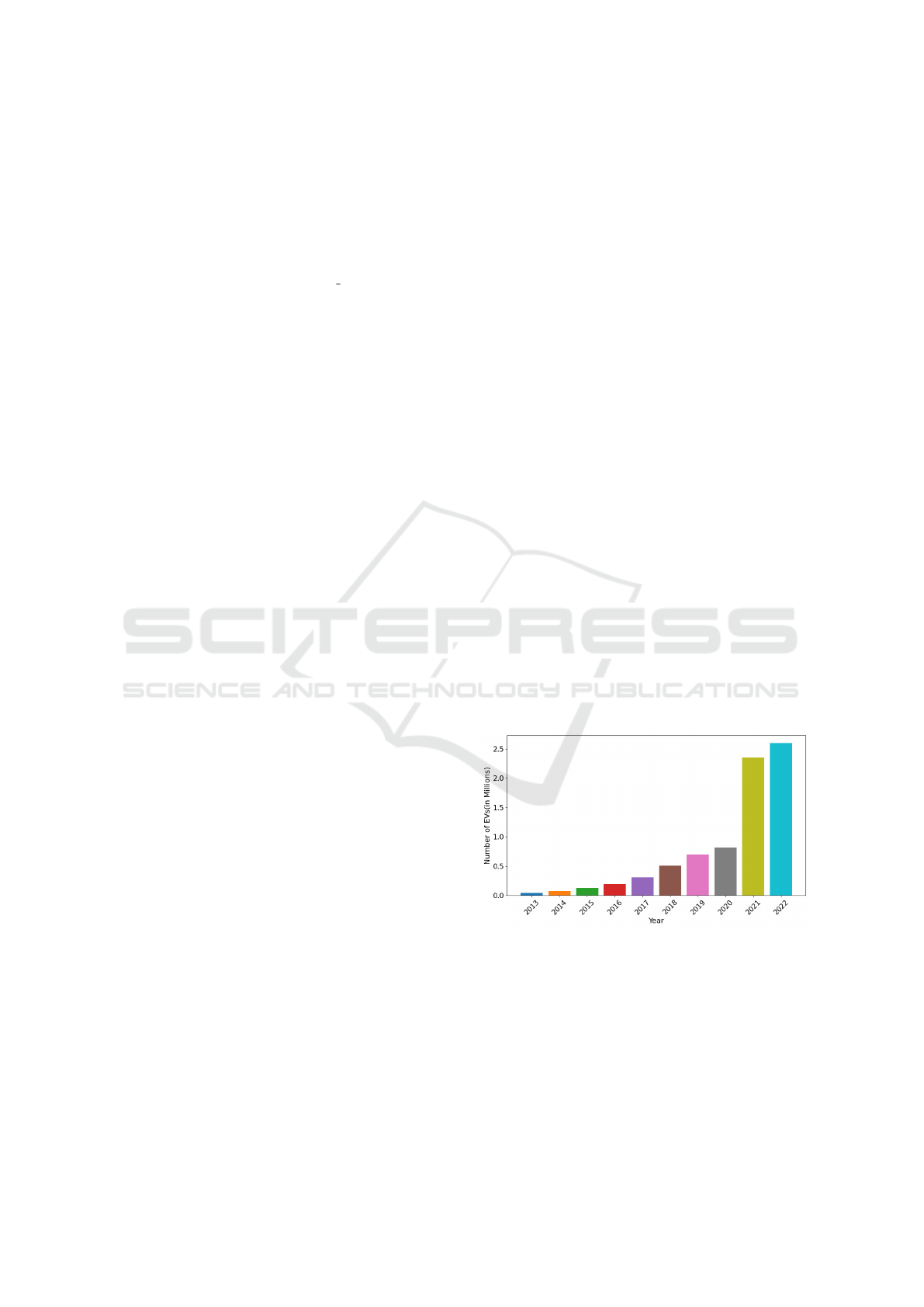
and quieter. As evident from Fig.1, we can see that
these factors have led to a tremendous increase in the
sale of EVs.
Because of the mentioned advantages of EVs over
gasoline-powered vehicles, many countries such as
China, the United States, and some European coun-
tries are promoting the adoption of EVs.(International
Energy Agency (IEA), 2023). By 2040, there is ex-
pected to be a complete transition from traditional
vehicles to EVs, with the number of EVs exceeding
more than 250 million. This large-scale adoption of
EVs will reduce the emission of CHG significantly,
but it will also lead to a substantial increase in elec-
tricity demand (International Energy Agency, 2019).
This surge in electricity demand could pose the chal-
lenge of overloading the power grid, especially during
peak hours (Lopes et al., 2011).
Figure 1: Rise of EVs: Global Trend (International Energy
Agency, 2019).
Another challenge for the widespread adoption of
EVs is the gradual and non-ubiquitous deployment of
CSs. The current ratio for the number of EVs on each
CS is 135:1 (Bolt Earth, Year). With the increasing
number of EVs, the number of CSs to meet the de-
mand of EV users is very low, and this uneven ratio of
EVs to CS has led to anxiety among EV users, which
is popularly known as range anxiety. Range anxiety
164
Sharma, S. and Thakur, R.
EV-Connect: Energy Efficient & Incentive Cost Based Model for Range Anxious EVs with Multi-Hop Socially Assisted V2V Charging.
DOI: 10.5220/0013479000003944
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Internet of Things, Big Data and Security (IoTBDS 2025), pages 164-171
ISBN: 978-989-758-750-4; ISSN: 2184-4976
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

concerns EV users about the possibility that the vehi-
cle may run out of charge before reaching the nearest
CS or final destination. The range anxiety particu-
larly increases among EV users in areas where there
is limited availability of CSs, such as highways and
remote locations, or even at CSs having longer queues
(Kester et al., 2020), (Xiong et al., 2018).
EVs, also functioning as mobile energy storage
units, give rise to new concepts of energy trans-
fer such as Vehicle-to-Grid (V2G), Vehicle-to-Home
(V2H), and Vehicle-to-Vehicle (V2V), which are
evolving due to the advent bi-directional chargers
(Ucer et al., 2019). The concept of V2V charge ex-
change enables EV users to alleviate range anxiety by
transferring surplus charge from one EV to another
with a charge deficit. (Liu et al., 2013), (Dhungana
and Bulut, 2019). It allows EV users to get charged by
other EV users, especially during peak hours, when
charging demand is high. Thus, V2V charging can be
exploited to reduce the load on the power grid in that
area.
In the latest developments in the V2V charg-
ing framework, some efficient matching algorithms
such as stable-matching (Zhang et al., 2017), (Wang
et al., 2018), and maximum-matching (Zhang et al.,
2019) have been used to map the consumer EVs
with provider EVs. Apart from this, in (Bulut and
Kisacikoglu, 2017), a social model system has been
proposed, where an EV is mapped with either CS or
with another EV, having a surplus charge. They have
used the maximum weighted bipartite matching algo-
rithm. In (Zhang et al., 2019), (Shurrab et al., 2022b),
and (Shurrab et al., 2022a), authors have proposed
the charge sharing models that are cost-effective and
user satisfaction-based for EV users. Authors in
(Kim et al., 2018) have considered a dynamic pric-
ing scheme for off-peak and on-peak load time and
proposed a matching theory based on the charge re-
quested by an EV. Also, in (Bulut et al., 2019), authors
have proposed the probable trip-based EV charging
where consumer EV detour cost has been minimized.
Considering the high demands of EVs, authors in
(Yuan et al., 2022) have proposed an auction frame-
work to promote EVs to sell their excess energy, as
CSs often pose a threat to satisfy these demands. De-
spite all these advancements, some constraints, such
as trust, still make EV users hesitate to request the
charge from anonymous users.
Considering the trust constraints, we have pro-
posed the socially connected V2V charge-sharing
framework, which provides a trustworthy connection.
The incentive-based model offers a cost-effective so-
lution for anxious EVs. It is also an effective solution
to reduce the load on the power grid.
2 SYSTEM MODEL
Figure 2: System model consisting of the anxious EVs, non-
anxious EVs, and CSs.
As shown in Fig. 1, our system model consists
of N number of EVs, including both anxious and
non-anxious EVs, and C number of CSs. Here, anx-
ious EVs are charge deficient and experiencing range
anxiety, denoted as N
A
i
, i = 1, 2,.., N
A
; and non-
anxious EVs have a surplus charge to provide the
charging to anxious EVs in return for some incen-
tives, which are are denoted as N
N
j
, j = 1, 2, . . ..,N
N
,
and N
N
= (N – N
A
). Expanding the current V2V
charging framework, we have included a social met-
ric among EVs to establish a charge-sharing frame-
work. Social V2V charging is defined as V2V charg-
ing where social connection is established if EVs are
connected through some social networking platform
(Foursquare, 2024) such as Twitter, Facebook, etc.
We assume that the EVs are connected socially; based
on that, anxious EVs can request the charge from
other non-anxious EVs. We have defined a set of so-
cially connected anxious and non-anxious EVs as N
N
s
.
The range (Rg) of an EV is defined as the max-
imum distance it can travel in a specific amount of
charge. We have considered the EV user’s daily trip
distance as (D
t
) and an extra distance that an EV user
may travel additionally, (D
a
). Apart from this, the
range anxiety (RA) can be defined as:
RA = SoC − ε (1)
where, we have assumed ε is the threshold value
and State of Charge (SoC) is the current battery
charge of EV, which can be calculated as:
SoC = Rg − D
t
− D
a
(2)
Based on the evaluated value of RA an EV user
can be classified as anxious EV if it’s value is less than
zero; otherwise, they are classified as non-anxious
EVs.
To minimize the number of anxious EVs experi-
encing range anxiety, we have constructed a bipartite
graph to attain an optimal matching among EVs and
CSs. In this graph, vertices (V) represent EVs or CSs,
while the edges (E) represent the connection between
EV-Connect: Energy Efficient & Incentive Cost Based Model for Range Anxious EVs with Multi-Hop Socially Assisted V2V Charging
165

anxious EVs and CSs or between anxious and non-
anxious EVs. More formally,
|V | = (|N
A
| ∪ |N
N
| ∪ |N
N
s
| ∪ |C|), where (3)
N
A
is the set of all anxious EVs , N
N
is the set
of all non-anxious EVs, N
N
s
is the subset of all non-
anxious EVs having social relationship with anxious
EVs, and C is the set of all CSs . The total set of edges
for socially connected anxious vehicles with CSs (e
C
)
and with non-anxious vehicles (e
N
s
) is defined as:
e = (e
C
∪ e
N
s
) (4)
2.1 Charging Framework
In our proposed charging framework, we have con-
sidered the serviceable charging radius (SCR), within
which any charge deficit EV can obtain a charge from
any CS or from socially connected EV through V2V
charge sharing. The charging services for each anx-
ious EV are based upon its minimum detour distance
(additional distance traveled to reach a point off the
original route). The mapping of anxious EVs for our
charging framework is classified into the following
cases:
• For CS: Based on the mapping of anxious EVs
with CS within its SCR, the edges of bipartite
graph are defined as: ∀ j ∈ N
A
,∀k ∈ C
e( j,k) =
(
1 if RD( j) ≥ dist
k
j
0 otherwise
(5)
Where, RD(j) represents the remaining distance
of j
th
anxious EV, and the dist
k
j
is its trip distance
with k
th
CS.
• CS with V2V(CS+V2V): In contrast to CS, where
anxious EVs rely solely on CSs to get their re-
quired charge, we facilitate V2V charging here,
enabling them to obtain charge from other non-
anxious EVs. Non-anxious EVs with excess
charge will act as charge providers for anxious
EVs. By incorporating V2V charging, the num-
ber of anxious EVs is expected to reduce as the
available charging options increase.
e( j,k) =









1, if RD( j) ≥ dist
k
j
and
RqD( j) ≤ RD(k) − 2 ∗ dist
k
j
0 otherwise
(6)
∀ j ∈ N
A
,∀k ∈ C ∪ N
N
Here, RqD is the amount required distance de-
manded by anxious EV user.
• For Socially Assisted 1-Hop/2-Hop V2V: By in-
tegrating a social factor, this scenario expands
upon the CS with the V2V approach. Incorpo-
rating this social factor allows anxious EVs to be
mapped to non-anxious EVs based on their social
relationships.
e( j,k) =

















1, if RD( j) ≥ dist
k
j
and
RqD( j) ≤ RD(k) − 2 ∗ dist
k
j
and
X
j,k
0 otherwise
(9)
∀ j ∈ N
A
,∀k ∈ C ∪ N
N
S
where X
j,k
=
(
1, if j and k are friends
0, otherwise
Where X
j,k
is defined as a social tie between EVs,
with a value of 1 if j and k are directly connected
(1-hop V2V) or indirectly connected (2-hop V2V)
and 0 otherwise (Li et al., 2014).
Our aim is to maximize the matching among anx-
ious EVs with both non-anxious EVs and CSs.
The optimal matching for anxious EV is achieved
if it gets mapped with at most one socially con-
nected non-anxious EV or CS. We have calculated
the weight of matched edges as:
max
∑
∀i
Q
i
s.t.
Q
i
=
∑
∀ j ∈ N
N
∪ C ∪ N
N
s
k
im
,∀i ∈ N
A
(8)
∑
∀m∈ N
NA
∪ C ∪ N
N
s
k
im
≤ 1, ∀i ∈ N
A
(9)
∑
∀i∈ N
A
k
im
≤ 1, ∀m ∈ N
N
∪C ∪ N
N
s
(11)
k
im
=
(
1, if i is assigned to m
0, otherwise
(12)
2.2 Total Energy Consumption
Considering the total battery capacity of the EV as
B
EV
in KWh, and the required energy of an anxious
EV is E
A
(KWh). The E
A
depends upon the anxious
EV’s SoV and its mileage (Mil
EV
) in (Km/KWh) of
the anxious EV given as:
E
A
= SoV /Mil
EV
(13)
We have also assumed that the power transfer effi-
ciency for V2V and V2CS is η. Thus, the maximum
energy an anxious EV can receive (ρ
A
) is given as:
IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security
166

ρ
A
= η ∗ E
A
(14)
The above mentioned equation evaluates the ρ
A
for each anxious EV. Thus, the total energy consumed
(ρ
A
T
) by the mapped anxious EVs can be formulated
as:
ρ
A
T
=
∑
∀i∈N
A
ρ
A
i
(15)
The total energy for mapped anxious EVs with CSs is
given as: (ρ
A
avCT
), with open V2V as (ρ
A
avV T
) and with
socially connected EVs as (ρ
A
avST
). Thus, the total av-
erage energy consumed by anxious EV for the case of
mapping with CS and socially connected V2V can be
determined as follows:
ρ
A
avCT
=
∑
ρ
A
C
/N
A
C
(16)
ρ
A
avV T
=
∑
ρ
A
V
/N
A
V
(17)
ρ
A
avST
=
∑
ρ
A
S
/N
A
S
(18)
The evaluation of the power grid load depends on the
number of EVs fulfilling their charging requirements
through CSs. The higher the number of anxious EVs
getting with CSs, the greater the load on the power
grid will be. Our proposed socially (1-hop/2-hop) as-
sisted V2V charging framework could be potentially
helpful in distributing the load solely from the power
grid, and it can be evaluated by using the factor named
reduction of load (ROL). ROL is the difference be-
tween the total energy consumed from the power grid
in the case of only CSs based framework and Socially
assisted charging framework, formulated as:
ROL = ρ
A
CT
′
− ρ
A
CT
(19)
Where, for our socially assisted model it is repre-
sented as ρ
A
CT
and for only CS case it can be repre-
sented as ρ
A
CT
′
.
2.3 Average Cost per EV
In our proposed cost model, we have defined the two
types of costs: Standard Price (SP
A
) and Incentive
Price (IP
A
). Both are priced at what anxious EVs
must pay to buy the charge. Also, both costs depend
upon the energy consumed by an anxious EV. The
price set by the grid to buy the surplus charge from
non-anxious EVs is prominently lower than the price
they will get from anxious EVs (Tushar et al., 2015).
Both the costs are defined and formulated as below:
2.3.1 Standard Price (SP
A
)
It refers to the unit price or actual price which is of-
fered by CSs to EVs ($/KWh). Thus, the average cost
per anxious EV with CSs (C
CS
) is given as:
C
CS
= ρ
A
CT
∗ SP
A
(20)
2.3.2 Incentive Price (IP
A
)
It refers to the discounted price offered to an anx-
ious EVs by non-anxious EVs. The incentive is deter-
mined based on the social and non-social relationship
between anxious and non-anxious EVs. Thus, the IP
A
is defined as follows:
IP
A
= (SP
A
− x%o f SP
A
)
(21)
Where x% is the percentage of discount offered on
the SP
A
, which will vary for V2V charging frame-
work basd on open V2V and social-V2V (1-hop/2-
hop) for anxious EVs. Thus, the incentive-based cost
for charging the anxious EV can be computed as:
C
EV
= ρ
A
ST
∗ IP
A
(22)
where, ρ
A
ST
is the average energy received by each
anxious EV from non-anxious EV during V2V charg-
ing.
3 PROPOSED APPROACH
In our proposed model, we construct a bipartite graph
comprising the set of vertices defining the anxious,
non-anxious, and CSs. An edge between the vertices
is established if the charge is shared between anx-
ious EV and CS or anxious and non-anxious EV. The
maximum weighted bipartite matching algorithm is
applied to discover the most optimal match (Kings-
ford, 2019). The energy-cost model can be used for
mapped anxious EVs that are socially connected to
non-anxious EVs and for mapped anxious EVs with
CSs in a bipartite graph. The average energy the anx-
ious EVs receive is determined for the cases (i). When
only CSs are present, (ii). When CS + open V2V
is present and (iii). When CS + socially connected
V2V charging option is also available. For open V2V
and socially assisted V2V charging, the evaluation in-
volves the same number of mapped anxious EVs as
in the case of only CSs. Still, due to the availabil-
ity of V2V charging, there will be a lesser number of
anxious EVs getting mapped with CSs.
4 SIMULATION RESULTS
4.1 Simulation Parameters
In this section, we evaluate the effectiveness of our
results, comparing them with the traditional V2V
charge-sharing framework (Bulut and Kisacikoglu,
2017). We have conducted our simulations in Java
EV-Connect: Energy Efficient & Incentive Cost Based Model for Range Anxious EVs with Multi-Hop Socially Assisted V2V Charging
167

Data: Set of demanding EVs (N
A
), set of
provider EVs (N
N
), set of CSs (C)
Result: The optimal matching for demanding
and provider EVs.
for j = 1 to |N
A
| do
Calculate SoV and RA based on
Equations (1), (2);
for k = 1 to |C| do
Establish bipartite graph G
1
for set
N
A
and C;
if (RD( j) > dist
k
j
) then
Establish E in G
1
// Construct the
edge set E;
end
end
for k = 1 to |C ∪ N
N
| do
Establish bipartite graph G
2
for N
A
and C ∪ N
N
;
if (RD( j) > dist
k
j
) and
(RqD( j) ≤ RD(k) − 2 ∗ dist
k
j
) then
Establish E in G
2
// Construct the
edge set E;
end
end
for k = 1 to |C ∪ N
N
∪ N
N
s
| do
Friends[ j][k] ← 1 if j and k are
friends, else −1;
Establish bipartite graph G
3
for set
N
A
and C ∪ N
N
// Initially empty;
if (RD( j) > dist
k
j
) and
(RqD( j) ≤ RD(k) − 2 ∗ dist
k
j
) and
X
j,k
then
Establish E in G
3
// Construct the
edge set E;
end
end
end
while G
1
,G
2
,G
3
do
Find perfect matching M using maximum
bipartite matching;
end
for j = 1 to |M| do
Compute ρ
A
;
Compute ρ
A
C
using ρ
A
S
and η;
Compute Total Energy ER
A
CT
and ER
A
ST
;
Calculate ROL according to Equation 19;
Calculate average cost C
CS
and C
EV
according to Equations 20, 22;
end
Algorithm 1: Mapping of anxious EVs to non-anxious
EVs and CSs based on matching of maximum weighted
bipartite graph.
using a custom discrete event simulator. We consider
a stochastic model for EVs where they can choose ei-
ther the nearest CS or V2V charging to get charged.
We evaluate the overall energy consumption and cost
for anxious EV users. The simulations study various
cases: Case 1: Comparing mappings of anxious EV
users with CSs, V2V charge sharing, and multi-hop
socio V2V charge sharing. Case 2: The effect of vari-
ation of social factor (%) on mapping of anxious EV
users with multi-hop socio V2V charge sharing. Case
3: The total average energy consumption by anxious
EV users. Case 4: Total average cost of buying the
charge for anxious EV users. All the simulations are
performed for 20 iterations and are averaged for vali-
dating our proposed model and also to obtain the uni-
formity in the result for randomly moving EV users
in our scenarios.
Table 1: Simulation Parameters.
Metric Value Unit
RNG Uniform distribution from 90 - 100 km
T
d
Uniform distribution from 60 - 90 km
E
d
Uniform distribution from 10 - 25 km
ε 25 km
S
f
0-100 %
RD Random distribution from 20 - 35 km
SP
A
Random Distribution from 10 - 20 $
x 5 - 20 %
η 0.85 and 0.90 %
N [30, 60, 90, 120, 150, 180] -
To mitigate the range anxiety among EV users, we
evaluate the effect of having V2V charging along with
CSs. The performance of our approach is measured
in terms of anxious EV users mapped. In our simu-
lations, we vary number of vehicles (V) from 30 to
180, with a step size of 30. There are 1/V CSs that are
randomly located in our scenario. Based on the value
of RA, as described in equation 3, we get our anxious
and non-anxious EV users.
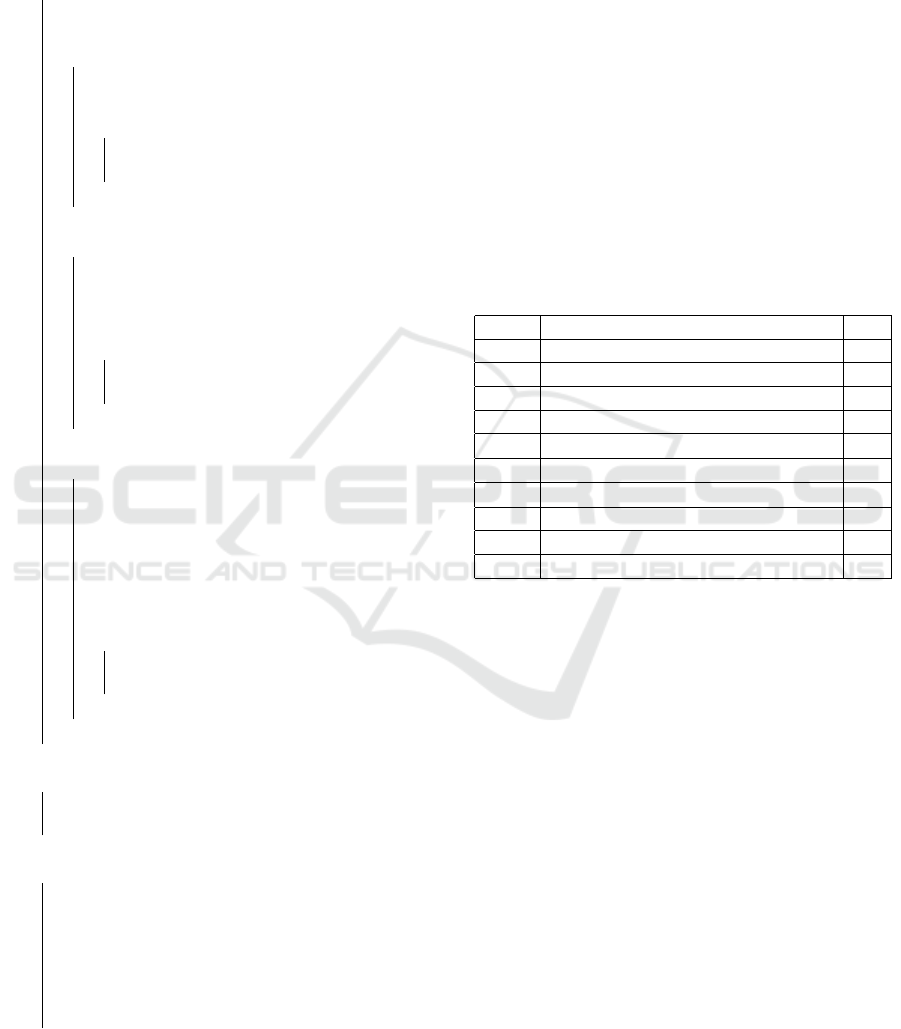
1. Mapped Anxious EVs Comparison: In Fig. 1,
we performed the simulation where we consid-
ered anxious and non-anxious EVs, and CSs. We
compare our proposed multi-hop-socially assisted
V2V charging with the traditional V2V charging
framework. The figure shows that if we consider
V2V charge sharing along with CSs, the number
of mapped anxious EV users increases compared
to when only CSs are present.
2. Anxious EVs Blocked: From Fig. 1, we can con-
clude that more anxious EVs can be mapped af-
ter incorporating V2V charging and CSs. Fig. 2
shows the number of blocked EVs, i.e., the vehi-
IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security
168

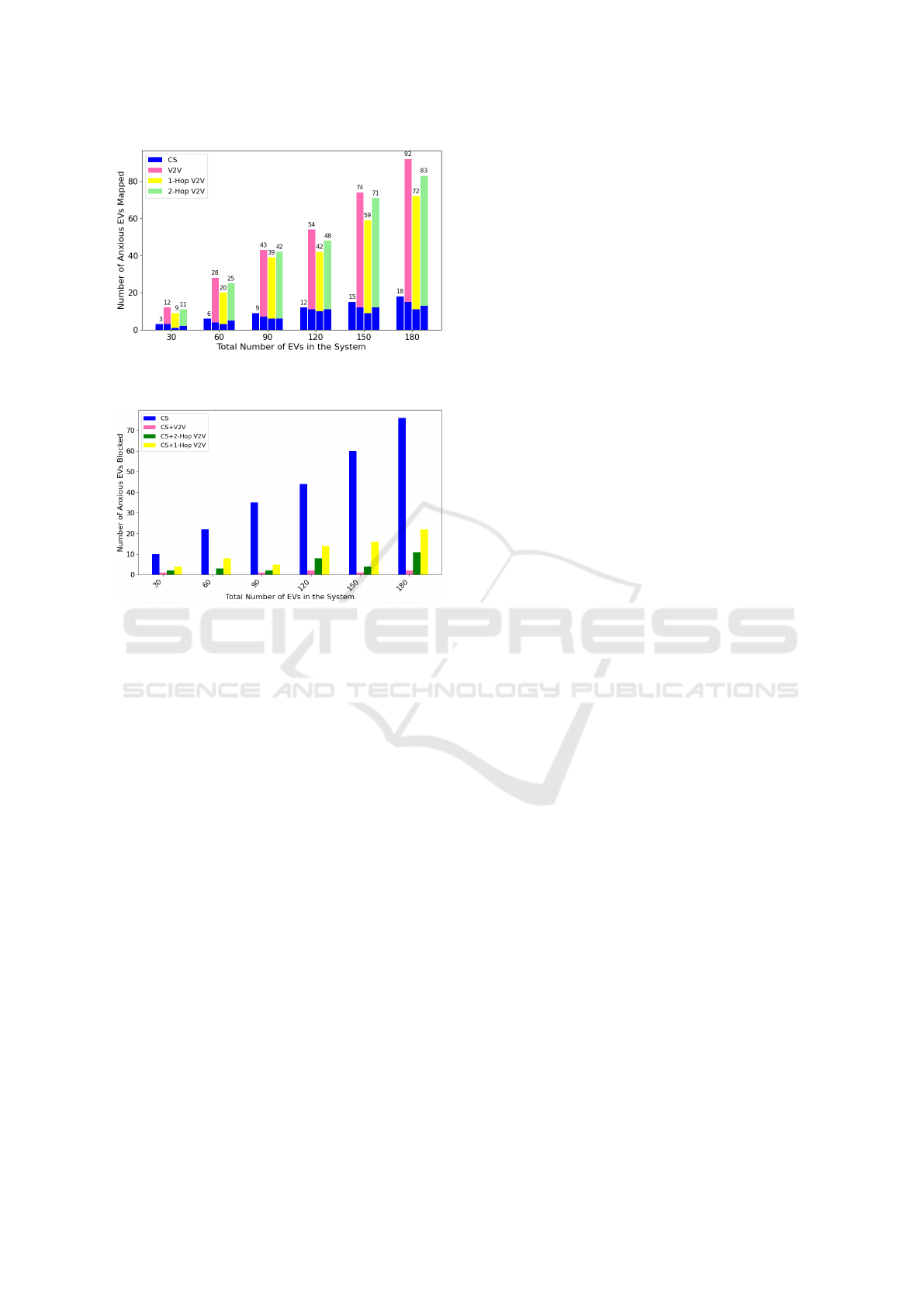
Figure 3: Number of Consumer EVs Mapped to Provider
EVs and CSs.
Figure 4: Number of Consumer EVs Mapped to Provider
EVs and CSs.
cles that could not get the required charge. We
can see from the figure that the maximum number
of anxious EVs who could not get the necessary
charge are in the case when only CSs are avail-
able. However, as we incorporate V2V charg-
ing, the blocked number of EVs decreases, which
means that more anxious EVs can get the required
charge. The minimum number of blocked EVs oc-
curs when both CSs and V2V charging are avail-
able. This is followed by 2-hop socially assisted
V2V charging, as EV users have more charging
options compared to 1-hop socially assisted V2V
charging.
3. Average Energy Consumption by Anxious EVs:
The average energy consumption for mapped anx-
ious EVs is calculated considering the value of
B
EV
to be 75KWh, allowing the vehicle to travel
up to 250Kms on a single charge. Thus, the Mil
EV
is calculated to be 3.33 km/kWh. The value of E
A
can easily be found using equation 13 considering
the value of SoV and Mil
EV
, which falls in the
range of 27.03KWh to 30.03KWh.
Due to some power loss for charging the EV from
CS and V2V, the efficiency for power transfer is
not ideally 1, but it is considered to be 0.9 for CS
and .85 for V2V. Thus, the maximum value of ρ
A
falls from 22.97KWh to 24.327KWh for CS and
25.25KWh to 27.07KWh for V2V for each anx-
ious EV. The minimum value of ρ
A
is evaluated
when the range anxiety has been triggered in the
anxious EV, i.e., at ε = 25Km, assessed in a range
of 5.75KWh to 6.76KWh. From the total number
of mapped anxious vehicles, the total average en-
ergy consumed is evaluated for the following two
cases:
(a) With V2V charging framework: Fig. 4 shows
the total average energy consumption from
CSs for V2V, and our social-assisted charging
framework falls in the range of 27 KWh to
235KWh. With the increase in area and the
number of vehicles, most of the charging re-
quirement is accomplished by the V2V charg-
ing framework. Thus, the minimum value of
the load on the power grid ρ
A
CT
′
min
is 27KWh
for the case when CS=3 and the total number
of EVs = 30. The maximum value of the load
on the power grid or the value of ρ
A
CT
′
max
is
235KWh for the case when CS=18 and the total
number of EVs = 180.
(b) Wihout V2V charging framework: From Fig. 4,
the precise observation can be made that with
only CS possibilities, the minimum value of
ρ
A
CT min
is 278KWh for CS=30 and a total num-
ber of EVs= 30 to meet the demand of ex-
act number of anxious EVs through CS only.
The maximum value of ρ
A
CT max
is 1335KWh for
CS=180, and the total number of EVs=180 for
the same number of anxious EVs through CS
only.
Thus the minimum value of ROL for total num-
ber of EVs to be 30 is 251Kwh. And the maxi-
mum value of ROL for the total number of EVs
to be 180 is 1100KWh. And it can be concluded
that our model helped significantly in reducing
the load on grid along with secure charge sharing
framework.
4. Average Cost for Anxiuos EVs: We have con-
sidered the SP
A
for charging the anxious EVs
through CSs and the IP
A
for charging the anxious
EVs through V2V charging infrastructure which
is categorized into the three cases based on the re-
lation they maintain either open V2V or they are
socially connected. All the three cases are men-
tioned as below:
(a) Open V2V charging- For V2V charging frame-
work, the anxious EVs are offered with the dis-
count (x) ranging from 5% to 10% on the (SP
A
).
(b) 2-Hop socially assisted V2V charging - So-
EV-Connect: Energy Efficient & Incentive Cost Based Model for Range Anxious EVs with Multi-Hop Socially Assisted V2V Charging
169

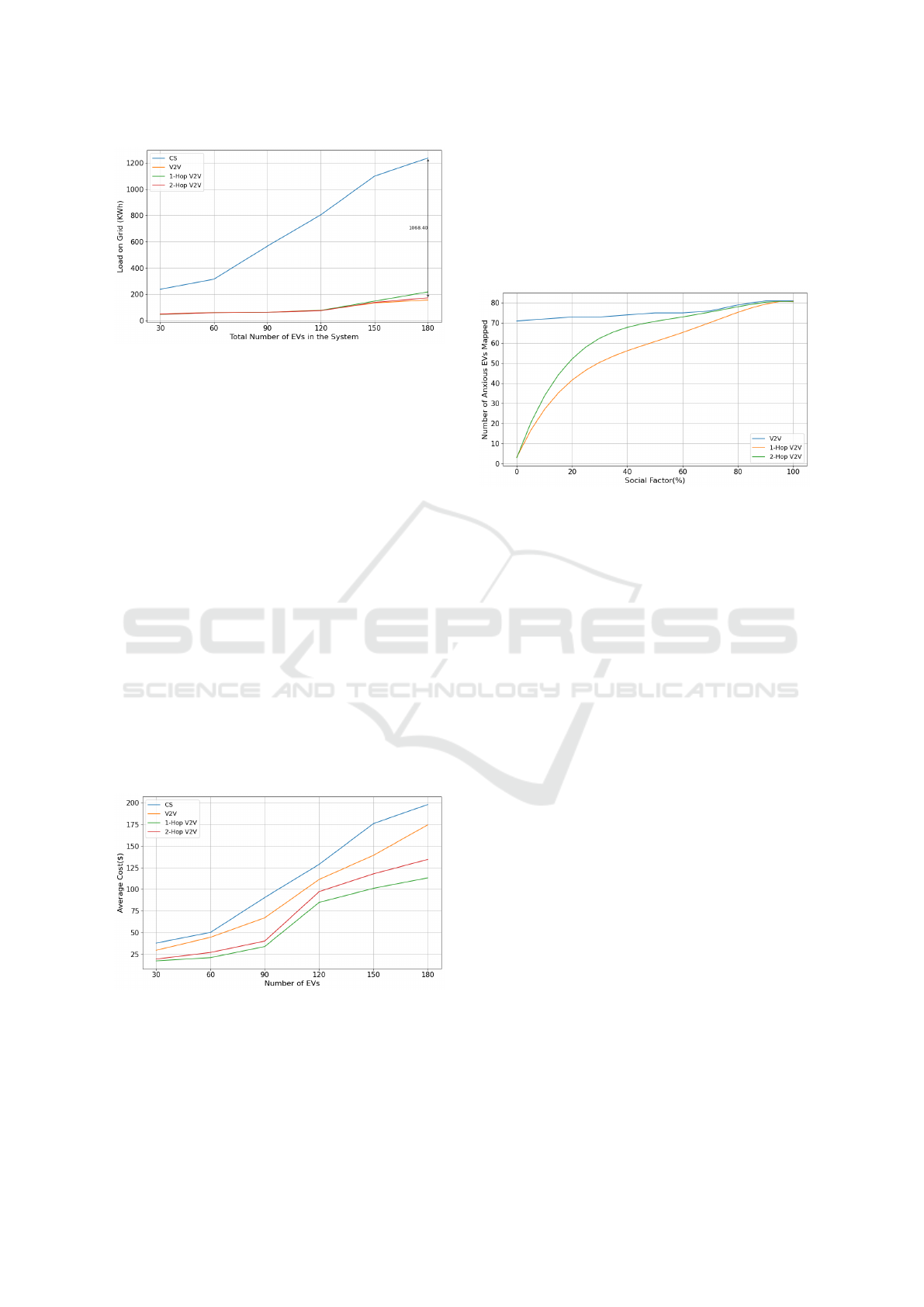
Figure 5: Average energy consumption by mapped anxious
EVs to CS (KWh).
cially assisted charging framework allows the
EV users of having higher discounts in com-
parison to open V2V, thus resulting in the lower
average cost. Here, anxious EVs will be offered
a discount (x) ranging from 10% to 15% on the
SP
A
.
(c) 1-Hop socially assisted V2V charging - In this
case, anxious EVs are offered with maximum
discount (x) ranging from 15% to 20% on the
IP
A
. The discount is maximum as compared to
other charging options as they share the direct
social relationship.
Fig. 6 shows that incentive based average cost
framework for 1-hop, 2-hop and V2V is signifi-
cantly lower as compared to standard average cost
for only CS based cost framework. Thus, for
socially assisted 1-hop V2V charging framework
the value ranges from $17.51 to $ 113.29, for 2-
hop $19.57 to$134.56, for open V2V $29.78 to
$174.53 and for only CS based charging frame-
work it ranges from $38.05 to $197.94.
Figure 6: Average cost($).
5. Impact of Social Factor (S
f
): To analyze the ef-
fect of socially connected EVs on range anxi-
ety, we have considered three cases such as 1-
hop, 2-hop, and open V2V charge-sharing frame-
work. And the value of S
f
is varied from 0 to
100%. We can see from Fig. 7 that as the S
f
in-
creases for 1-hop and 2-hop, more anxious EVs
are getting mapped to non-anxious EVs and the
results aligns with the open V2V charging frame-
work, which validates our socially assisted charg-
ing framework and additionally giving the secure
charging framework.
Figure 7: Mapped anxious EVs with increase of social fac-
tor.
5 CONCLUSION
In this paper, we presented the cost-aware socially
connected V2V charging framework for addressing
the range of anxiety in anxious EVs by enabling them
to buy energy from other non-anxious EVs with sur-
plus charge on discounted price.
We performed simulations for various cases with
and without V2V charging to assess the system’s
performance. The proposed social charging system
grants EV drivers complete control over their charg-
ing needs while safeguarding their privacy. After
closing analyzing the mapping of lesser anxious EVs
to CSs gave the insight that socially assisted V2V
charging framework also significantly reduces the
load on the power grid. It establishes a mutually ben-
eficial environment for EV energy sellers and buy-
ers. As part of our future work, we plan to investigate
the impact of other simulation parameters on the sys-
tem’s outcomes. Additionally, we will explore pricing
mechanisms, such as auctions, within social market
scenarios for this charging system.
REFERENCES
Bolt Earth (Year). Indian ev charging infras-
tructure by 2030. https://bolt.earth/blog/
indian-ev-charging-infrastructure-by-2030. Ac-
cessed: Date.
Bulut, E. and Kisacikoglu, M. C. (2017). Mitigating Range
IoTBDS 2025 - 10th International Conference on Internet of Things, Big Data and Security
170

Anxiety via Vehicle-to-Vehicle Social Charging Sys-
tem. In IEEE 85th Vehicular Technology Conference
(VTC Spring), pages 1–5.
Bulut, E., Kisacikoglu, M. C., and Akkaya, K. (2019).
Spatio-Temporal Non-Intrusive Direct V2V Charge
Sharing Coordination. IEEE Transactions on Vehic-
ular Technology, 68(10):9385–9398.
Dhungana, A. and Bulut, E. (2019). Peer-to-peer energy
sharing in mobile networks: Applications, challenges,
and open problems. Ad Hoc Networks, 97:102029.
Foursquare (2024). Foursquare. https://foursquare.com/.
Accessed: 2024-08-26.
Frade, I., Ribeiro, A., Gonßalves, G., and Pais Antunes,
A. (2011). Optimal location of charging stations for
electric vehicles in a neighborhood in lisbon, portu-
gal. TRR, 2252.
International Energy Agency (2019). Global EV Outlook
2019. IEA, Paris. Licence: CC BY 4.0.
International Energy Agency (IEA) (2023). Global ev out-
look 2023. Technical report, IEA, Paris. Licence: CC
BY 4.0.
Kester, J., Sovacool, B. K., Noel, L., and Zarazua de
Rubens, G. (2020). Rethinking the spatiality of nordic
electric vehicles and their popularity in urban environ-
ments: Moving beyond the city? Journal of Transport
Geography, 82:102557.
Kim, O. T. T., Tran, N. H., Nguyen, V., Kang, S. M., and
Hong, C. S. (2018). Cooperative between v2c and
v2v charging: Less range anxiety and more charged
evs. In 2018 International Conference on Information
Networking (ICOIN), pages 679–683.
Kingsford, C. (2019). Maximum bipartite matching. Maxi-
mum Bipartite Matching.
Li, Y., Wu, T., Hui, P., Jin, D., and Chen, S. (2014). Social-
aware d2d communications: Qualitative insights and
quantitative analysis. IEEE Communications Maga-
zine, 52(6):150–158.
Liu, C., Chau, K. T., Wu, D., and Gao, S. (2013). Opportu-
nities and challenges of vehicle-to-home, vehicle-to-
vehicle, and vehicle-to-grid technologies. Proceed-
ings of the IEEE, 101(11):2409–2427.
Lopes, J. A. P., Soares, F. J., and Almeida, P. M. R. (2011).
Integration of electric vehicles in the electric power
system. Proceedings of the IEEE, 99(1):168–183.
Shurrab, M., Singh, S., Otrok, H., Mizouni, R., and Khad-
kikar (2022a). An efficient vehicle-to-vehicle (v2v)
energy sharing framework. IEEE Internet of Things
Journal, 9(7):5315–5328.
Shurrab, M., Singh, S., Otrok, H., Mizouni, R., Khad-
kikar, V., and Zeineldin, H. (2022b). A stable match-
ing game for v2v energy sharing–a user satisfaction
framework. IEEE Transactions on Intelligent Trans-
portation Systems, 23(7):7601–7613.
Tushar, W., Chai, B., Yuen, C., Smith, D. B., Wood, K. L.,
Yang, Z., and Poor, H. V. (2015). Three-party en-
ergy management with distributed energy resources in
smart grid. IEEE Transactions on Industrial Electron-
ics, 62(4):2487–2498.
Ucer, E., Buckreus, R., Kisacikoglu, M. C., Bulut, E., Gu-
ven, M., Sozer, Y., and Giubbolini, L. (2019). A flexi-
ble v2v charger as a new layer of vehicle-grid integra-
tion framework. In 2019 IEEE Transportation Elec-
trification Conference and Expo (ITEC), pages 1–7.
Wang, M., Ismail, M., Zhang, R., Shen, X., Serpedin, E.,
and Qaraqe, K. (2018). Spatio-temporal coordinated
v2v energy swapping strategy for mobile pevs. IEEE
Transactions on Smart Grid, 9(3):1566–1579.
Xiong, Y., Gan, J., An, B., Miao, C., and Bazzan, A. L. C.
(2018). Optimal electric vehicle fast charging sta-
tion placement based on game theoretical framework.
IEEE Transactions on Intelligent Transportation Sys-
tems, 19(8):2493–2504.
Yuan, Y., Jiao, L., Zhu, K., and Zhang, L. (2022). Schedul-
ing online ev charging demand response via v2v auc-
tions and local generation. IEEE Transactions on In-
telligent Transportation Systems, 23(8):11436–11452.
Zhang, R., Cheng, X., and Yang, L. (2017). Stable matching
based cooperative v2v charging mechanism for elec-
tric vehicles. In 2017 IEEE 86th Vehicular Technology
Conference (VTC-Fall), pages 1–5.
Zhang, R., Cheng, X., and Yang, L. (2019). Flexible energy
management protocol for cooperative ev-to-ev charg-
ing. IEEE Transactions on Intelligent Transportation
Systems, 20(1):172–184.
EV-Connect: Energy Efficient & Incentive Cost Based Model for Range Anxious EVs with Multi-Hop Socially Assisted V2V Charging
171