Training Telemedicine Robots: A Path Planning Optimization Method

for Educational and Medical Application

Artur Samojluk

and Aleksandra Szpakowska

Faculty of Mathematics and Computer Science, University of Warmia and Mazury in Olsztyn, Poland

Keywords:

Educational Technology, Path Planning, Mereological Potential Field Algorithm, Educational Telemedicine

Robot, Complex Labyrinth Map.

Abstract:

In this paper, we present a Path Planning Optimization Method (PPOM) designed for educational telemedicine

robots. Based on the mereological potential ﬁeld algorithm, it integrates data preprocessing and optimization

tools to enhance efﬁciency. Our method addresses navigation challenges in complex, tightly spaced med-

ical environments while emphasizing its educational value. By incorporating data selection, cleaning, and

transformation, PPOM enables efﬁcient path planning in maze-like layouts with long, narrow corridors, mim-

icking real-world hospital wards and patients’ homes. This equips telemedicine robots to navigate local traps

and tight spaces, providing a robust framework for training students and professionals in robot navigation

and decision-making. Simulation results conﬁrm PPOM’s high performance in complex environments. The

algorithm ensures precise navigation and effective obstacle avoidance, making it ideal for telemedicine ap-

plications. Unlike classical methods that struggle with blocked nodes, PPOM selects sectors, minimizing

obstructions and improving computational efﬁciency. This enhances route passability, optimization, and reli-

ability in dynamic environments.

1 INTRODUCTION

With the changing world, the expectations and skills

of computer science students in using future technolo-

gies, such as telemedicine and robotics, are evolving.

To enhance student learning in the UWM lab, we built

obstacle models simulating hospital room conditions

and tested robot performance in these settings. Dur-

ing the experiments, we identiﬁed speciﬁc obstacle

conﬁgurations (beds, sanitation, medical devices) that

introduced a new challenge in path planning: posi-

tioning obstacles in a way that creates local traps for

the robot. Analyzing these critical cases using two

mathematical methods led to the development of a

path planning algorithm that effectively resolves this

issue. As part of an educational activity, students

implemented the algorithm model into a robot and

conducted successful physical simulations. The algo-

rithm is easily adaptable for new educational robots

and has broader applications in indoor path planning

for small robots. The successful implementation of

this algorithm has inspired students to engage more

https://orcid.org/0000-0001-5822-2210

https://orcid.org/0000-0003-2641-8846

deeply in scientiﬁc research, leading some to join the

robotics research club. The project’s execution marks

both a scientiﬁc and educational success.

It is worth mentioning that the use of team-

work and active learning methods in this project con-

tributed to the development of students’ competencies

in terms of cooperation and responsibility for joint ac-

tions. According to the results of the research (Planas-

Llad

o et al., 2021), self-assessment and peer assess-

ment in the context of teamwork in higher education

can signiﬁcantly affect the development of students’

interpersonal and professional competencies, which

was also reﬂected in our project implementation. In

addition, the use of collaborative learning techniques,

such as group work and sharing knowledge and re-

sponsibility for the implementation of tasks, is in

line with the assumptions presented in the publication

(Taxirovna, 2024), (Falcione et al., 2019). Interac-

tive student engagement improves cognitive abilities

in the learning process and affects the overall educa-

tional development of young people. The study (Oth-

man and Zaın, 2015) assessed the effect of online col-

laboration on the cognitive abilities of programming

students, especially in the area of logical thinking and

problem-solving skills. The results showed that after

Samojluk, A. and Szpakowska, A.

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application.

DOI: 10.5220/0013481400003932

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Conference on Computer Supported Education (CSEDU 2025) - Volume 1, pages 147-157

ISBN: 978-989-758-746-7; ISSN: 2184-5026

147

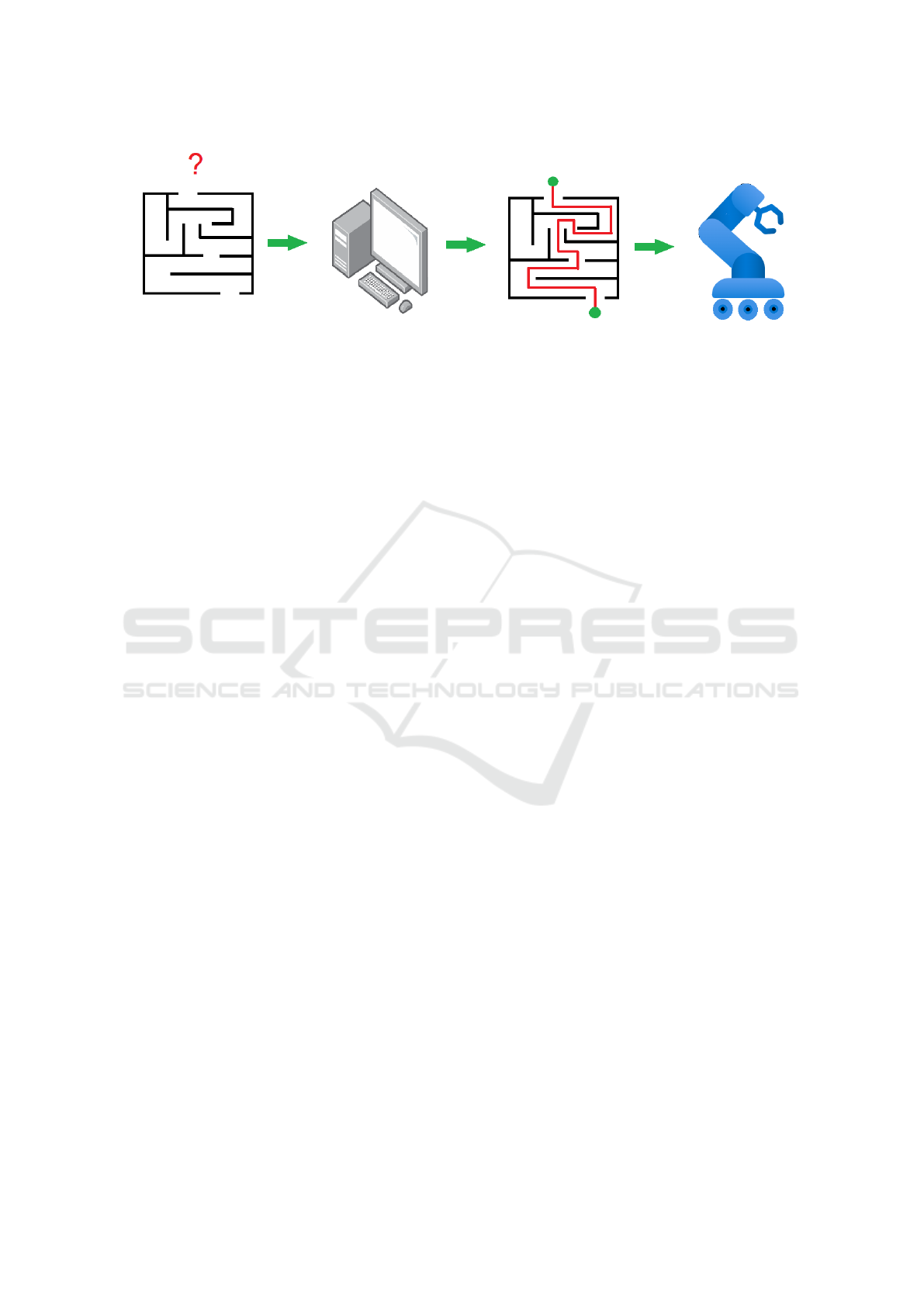
Figure 1: Graphic representation of system operation - path planning in a labyrinth.

the interactive session, the number of students with

a high level of logical thinking increased from 30%

to 51.7%, which is an improvement of 21.7%. Addi-

tionally, when analyzing the effectiveness of solving

programming tasks, it was shown that 53.3% (8 out of

15 groups) were able to solve more complex problems

requiring analysis. These results indicate that interac-

tive teaching methods based on online collaboration

can signiﬁcantly support the development of students’

cognitive abilities in the area of programming. This

theory is also supported by the study (Nurdin and Se-

tiawan, 2016), in which interactive technologies in-

creased students’ cognitive abilities. These methods

not only increase student engagement but also pro-

mote the development of critical thinking and the abil-

ity to solve problems independently. Thanks to this

project, it was possible to achieve not only educa-

tional goals but also to awaken in students a passion

for further development in robotics and automation.

The main idea of this study on optimizing the path

planning process for telemedical robots came from

the key methodology developed by Polkowski and

Skowron (Polkowski and Skowron, 1996). The re-

sults of this work, which utilized mereological po-

tential ﬁelds, were applied in a subsequent pub-

lication (Polkowski and O

smiałowski, 2008), and

smiałowski and Polkowski, 2010). The motivation

for researching using and improvement of path plan-

ning algorithms came from the implementation of an-

other telemedical project. The mentioned project fo-

cuses on creating a voice telemedical system that en-

ables remote and automated medical interviews with

patients, commissioned by the National Centre for

Research and Development in Poland. During the

project implementation, it was observed that the sys-

tem could more effectively fulﬁll it is assumptions in

a hospital context if it were possible for medical inter-

views could be conducted directly with patients. This

led to the idea of a robot that could monitor patients

in hospital wards and, if necessary, approach the bed

of a patient to conduct a conversation. Analysis re-

vealed that the layout of beds in the hospital, and it

is equipment, create a kind of labyrinth from the per-

spective of the robots, making it difﬁcult to quickly

reach the destination. To the robot efﬁciently reach

the designated location without disrupting the staff of

the medical, taking into account the correct side of

the bed of the patient, it must be able to rapidly learn

the environment and dynamically plan paths to des-

ignated points. The research problem is associated

with the need to endow the robot with ’human spatial

intuition’ to enable planning the trip to the chosen lo-

cation (the problem of route passability). Thus, the

demand for quick and safe access to the telemedical

robot became the key motivation for conducting re-

search in this ﬁeld.

This study aims to enhance the path planning pro-

posed by Szpakowska et al. in 2023 (Szpakowska

et al., 2023) which utilizes a mereological potential

ﬁeld algorithm by applying an additional decision-

making system. The mentioned extension focuses on

reducing the number of generated potential ﬁelds by

analyzing and concerning deﬁned sectors that repre-

sent the split part of a map. Additionally, there is an

effort to modify an existing path planning algorithm

by adding new functions like checking if two cho-

sen potential ﬁelds have not been connected by a line

crossing an obstacle ﬁeld. Furthermore, this paper ap-

plies increased automation to the path-planning algo-

rithm. The process begins by generating the mereo-

logical potential ﬁeld, and after that ﬁltering the list

of potential ﬁelds by removing unnecessary data. The

action of reducing data starts from map analysis. A

decision-making system checks if between two close

sectors exists any vertical or horizontal connection, if

so the system treats sectors as passable. The num-

ber of potential sector combinations could be sub-

stantial; hence, one of the deciding factors is select-

ing the combination with the fewest sectors. The al-

gorithm analyzes sectors until it gets the list of con-

nected sectors from the determined start to the goal.

The returned sector list contains all potential ﬁelds

that fall within them. The truncated list of potential

ﬁelds in which any possible path certainly exists is

CSEDU 2025 - 17th International Conference on Computer Supported Education

148

passed to the path search algorithm, thanks to which

we have got the accurate path. The proposed solu-

tion solves the problem of complicated maps contain-

ing many obstacles. Examples of such an environ-

ment are hospital wards or homes of the patients. The

next sections will show the effectiveness of the pro-

posed algorithm. The mentioned research takes into

account labyrinthine cases and environments charac-

terized by long narrow corridors similar to different

types of medical environments. To get better results

we applied a path-planning algorithm, which gave us

a clear, unambiguous route. Such operations pro-

vided the optimal path for the telemedical robot. The

next part of the study will explore further developing

a decision-making system using principles of rough

sets.

1.1 Educational Applications

Interactive Learning Tools. The proposed algo-

rithm serves as a good platform for teaching robotics,

allowing students to gain practical understanding

of path-planning algorithms in realistic environments.

Development of Analytical Thinking. Students

learn to analyze problems and design solutions,

which strengthens their ability to think logically

and strategically in situations that require quick

decision-making.

Simulations in Education. The use of physical

simulations in laboratories enables students to gain

experience in environments resembling real-world

scenarios, enhancing their practical skills.

Interdisciplinary Integration. The project encour-

ages collaboration among students from different

ﬁelds, such as computer science, mechanics, and

medicine, promoting an interdisciplinary approach to

learning and problem-solving.

Supporting Innovation. The algorithm inspires stu-

dents to experiment with their own modiﬁcations and

develop new features, supporting creativity and inno-

vative thinking.

1.2 Research Applications

Algorithm Optimization. The PPOM method en-

ables further reﬁnement of path-planning algorithms,

increasing their efﬁciency in complex environments.

Applications in Medicine. The algorithm is specif-

ically designed to meet the unique needs of medical

environments, such as narrow corridors and crowded

spaces in hospitals.

Solutions for Dynamic Environments. The algo-

rithm can be adapted to rapidly changing conditions,

making it an ideal tool for research in dynamic and

adaptive robotics.

Collaboration in Multi-Robot Systems. The

algorithm supports synchronization and coordination

among multiple robots, opening new opportunities

for research in multi-agent systems.

Foundation for Further Research. The research

ﬁndings can serve as a basis for developing new

methods in robotics, mereology theory, and decision-

making algorithms, supporting the advancement of

emerging technologies.

2 ROUGH SET THEORY AND

ROUGH MEREOLOGY

Rough set theory (Pawlak, 1992) employs lower and

upper approximations to facilitate the classiﬁcation of

ambiguous data, providing a means to navigate uncer-

tainty without the need for additional external param-

eters. Rough sets have found extensive applications

in various ﬁelds, notably in data analysis, where they

aid in uncovering hidden patterns and relationships

within imprecise datasets (Komorowski et al., 1999).

Rough mereology (Polkowski and Skowron, 1996), a

subsequent development in this domain, extends the

foundational principles of rough sets to encompass

the concept of ’part to a degree’. Developed to ad-

dress the limitations in traditional mereology, rough

mereology allows for a more ﬂexible understanding

of part-whole relationships in contexts where preci-

sion is unattainable. The reasoning based on rough

mereology introduces the concept of rough inclusion,

denoted as µ(x, y, r). This relation posits that x is a part

of y to a degree of at least r. Given our focus on spatial

objects, the rough inclusion is expressed as µ(X,Y, r)

if and only if

|X∩Y |

>= r, where X and Y represent n-

dimensional solids and |X| signiﬁes the n-volume of

X. The synergy between these two theories provides

a comprehensive framework for the analysis of non-

binary, uncertain data structures. The ongoing evolu-

tion of rough set theory and rough mereology contin-

ues to contribute signiﬁcantly to advancements in data

science, offering new perspectives and methodologies

for dealing with the complexities of modern data.

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application

149

3 BASIC POTENTIAL FIELDS

ALGORITHM AND SOME

UNIQUE ARRANGEMENT OF

OBSTACLES

We would like to begin by discussing the funda-

mental mechanisms of the potential ﬁelds algorithm

(Polkowski and Skowron, 1996), it is advantages,

as well as the critical situations that can arise when

using this algorithm. The concept of the potential

ﬁelds algorithm was introduced in works (Polkowski

and O

smiałowski, 2008) and (O

smiałowski and

Polkowski, 2010), (Osmialowski, 2011) in the last

paper special variant named the Square Fill Algo-

rithm. The mentioned method already was mod-

iﬁed and later presented in Polkowski (Polkowski

et al., 2018), Zmudzinski and Artiemjew (Zmudzin-

ski and Artiemjew, 2017), Gnys (Gny

s, 2017) and

Szpakowska, Artiemjew and Cybowski (Szpakowska

et al., 2023) on which this paper based on.

3.1 Intersection Condition

The algorithm performs admirably in scenarios where

a limited number of obstacles are present. In cases

where the map offers ample open space for naviga-

tion, seamless operation is observed. However, chal-

lenges arise when applying the algorithm to maps re-

sembling mazes, characterized by a proliferation of

obstacles. In such instances, the algorithm occasion-

ally neglects crucial obstacle-avoidance rules, leading

to lapses in connecting the current ﬁeld with the most

strategically advantageous option in the given step,

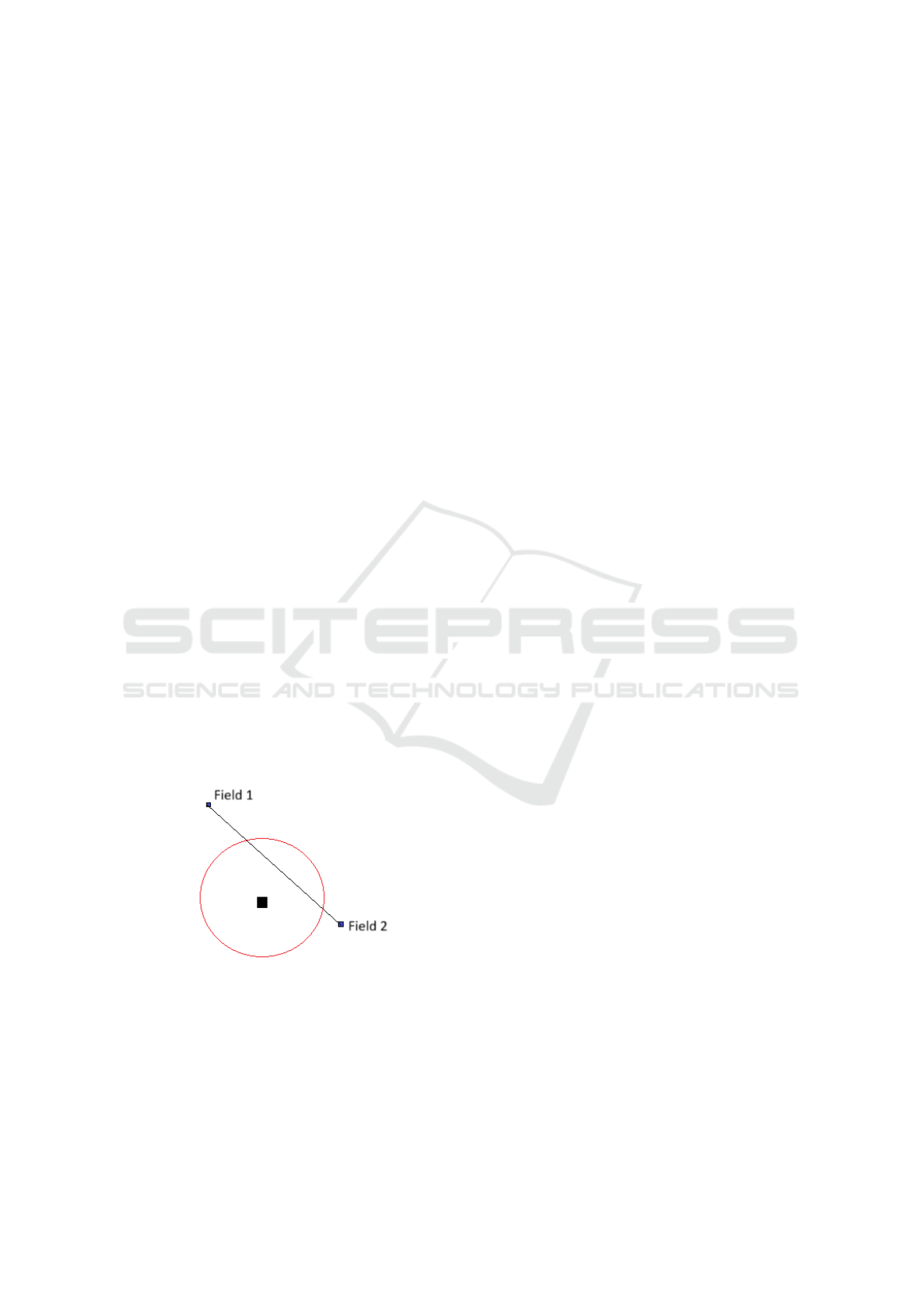
which is forbidden - see ﬁg.2.

Figure 2: Unexpected intersection between current poten-

tial ﬁeld and ’the most attractive ﬁeld’, which should not

appear.

To solve this unexpected action the intersection

checking was applied. A few steps were added to the

existing patch search algorithm (Szpakowska et al.,

2023) to improve the performance of the program.

Initially, each iteration of the path planning func-

tion involves the creation of a linear function between

the current and next potential ﬁelds. Subsequently, an

obstacle ﬁeld was established through the creation of

circular zones. The circle’s center coincided with the

obstacle’s center, and the radius was determined by a

parameter speciﬁed in the existing obstacle-checking

function.

The subsequent step focuses on verifying whether

the linear path intersects with any of the circular ob-

stacles. This was achieved by generating a series of

points along the path. The outcome, denoted as True

or False, determines the feasibility of establishing a

viable path between the two evaluated points, based

on the intersection or absence thereof with the obsta-

cle circles.

3.2 Unique Arrangement of Obstacles

The Mereological Potential Fields algorithm system-

atically extends from the goal towards the map bor-

ders, intelligently navigating to avoid obstacles. An

advantageous feature of this algorithm lies in it is

capacity to comprehensively explore the entire map.

The user can effortlessly discern a goal location based

solely on the spatial arrangement, leveraging the ac-

cumulation of potential ﬁelds.

Given this interdependence, it becomes evident

that the crucial factor is the strategic placement of

potential ﬁelds, inﬂuencing not only the goal posi-

tion but also delineating the locations of obstacles.

Despite the widespread presence of potential ﬁelds

throughout the whole map, their deployment may ap-

pear excessive in scenarios where a direct, optimal

path is sufﬁcient.

Conversely, the abundance of potential ﬁelds

presents numerous opportunities. In intricate scenar-

ios characterized by a substantial number of obsta-

cles, the increased density of generated ﬁelds proves

invaluable for identifying alternative routes. Regret-

tably, challenges arise in cases where the fundamen-

tal path-planning algorithm struggles to cope, partic-

ularly in more intricate scenarios.

Figure 3 shows one of the examples of critical

cases when the path was not found. The algorithm

ﬁnishes work with the result of getting stuck in one

place, without any possibility to ﬁnd the goal.

Map Legend:

• One-color painted square represents the start

point,

• Extreme markers determine map borders,

• Circles with squares describe obstacles and those

ﬁelds,

• Goal is represented by a marker

CSEDU 2025 - 17th International Conference on Computer Supported Education

150

Figure 3: Critical case with determined goal position on

point (490,490) - down left corner, and start point in (10,10)

- top right corner.

To solve the problem of complex cases we propose

the Route selection system (read Section 6)

4 ADDRESSING THE

CHALLENGE OF UNIQUE

ARRANGEMENT OF

OBSTACLES

The basic potential ﬁelds algorithm generated a se-

ries of exceptions that prevented ﬁnding a path to the

destination. After analyzing cases where such a situ-

ation occurred (see ﬁg. 3), it was observed that they

were associated with directing the path into a closed

area (without passage), often characterized by a nar-

row entrance. Consequently, the algorithm in it is cur-

rent form was unable to ﬁnd a return path. To avoid

this scenario, an improvement was introduced, con-

sisting of a probabilistic determination of whether the

designated path has a realistic chance of reaching the

destination. This approach involves a general exami-

nation of the map and identiﬁcation of areas that could

be critical for planning a detailed route. Subsequently,

the basic algorithm is activated and steered towards

areas that have undergone preliminary examination

and, problematically, present a higher likelihood of

passage.

5 NEW CONCEPTION AND

DEVELOPMENT OF

MEREOLOGICAL POTENTIAL

FIELD ALGORITHM

In this section, the mechanics of the algorithm PPOM

are presented, along with a sequential description of

the actions that should be performed in a speciﬁed or-

der:

1. Obstacles are introduced onto the map, in this case

in the form of circles. Points overlapping with ob-

stacles are removed.

2. The points (potential ﬁelds) are generated on

a 2D map with coordinates (X,Y ) concerning

the rules of generating mereological potential

ﬁelds (Polkowski and O

smiałowski, 2008),(Os-

mialowski, 2011), using the square ﬁll algo-

rithm (see references (Osmialowski, 2011), (Sz-

pakowska et al., 2023)).

3. The map is divided into sectors, with the mini-

mum division being 2x2 (4 sectors). The compu-

tational complexity increases with a higher divi-

sion of the map into sectors. A greater division

into sectors is recommended for maps with many

small, interconnected obstacles. Here, we use a

division into 3x3 (9 sectors), as per the following

scheme: We start numbering from the top left cor-

ner, numbering to the right.

An example of how the map is divided into sectors

is illustrated in Fig. 4.

4. For the sake of computation organization, sectors

are numbered starting from the top left corner, and

then from left to right (ﬁg. 4).

5. Every sector is subjected to a separate drivability

analysis. The algorithm checks simpliﬁed paths

in each sector for four directions: vertical, hori-

zontal, diagonal left, and diagonal right (see ﬁg.

4). Passable paths are marked in green, and im-

passable ones in red (ﬁg. 4). In total, 12 paths are

checked for each sector, and the overall drivabil-

ity of a sector is calculated as the ratio of passable

paths to the number of paths tested.

6. Building potential paths in a sector perspective.

We determine all possible paths through sectors,

starting from the deﬁned starting sector and end-

ing at the deﬁned ending sector. The path can only

move forward, changing direction vertically, hori-

zontally, or diagonally, without repeating sectors.

7. Analyzing possible paths. Each potential path is

analyzed for drivability and components such as

the number of obstacles, points, and whether the

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application

151

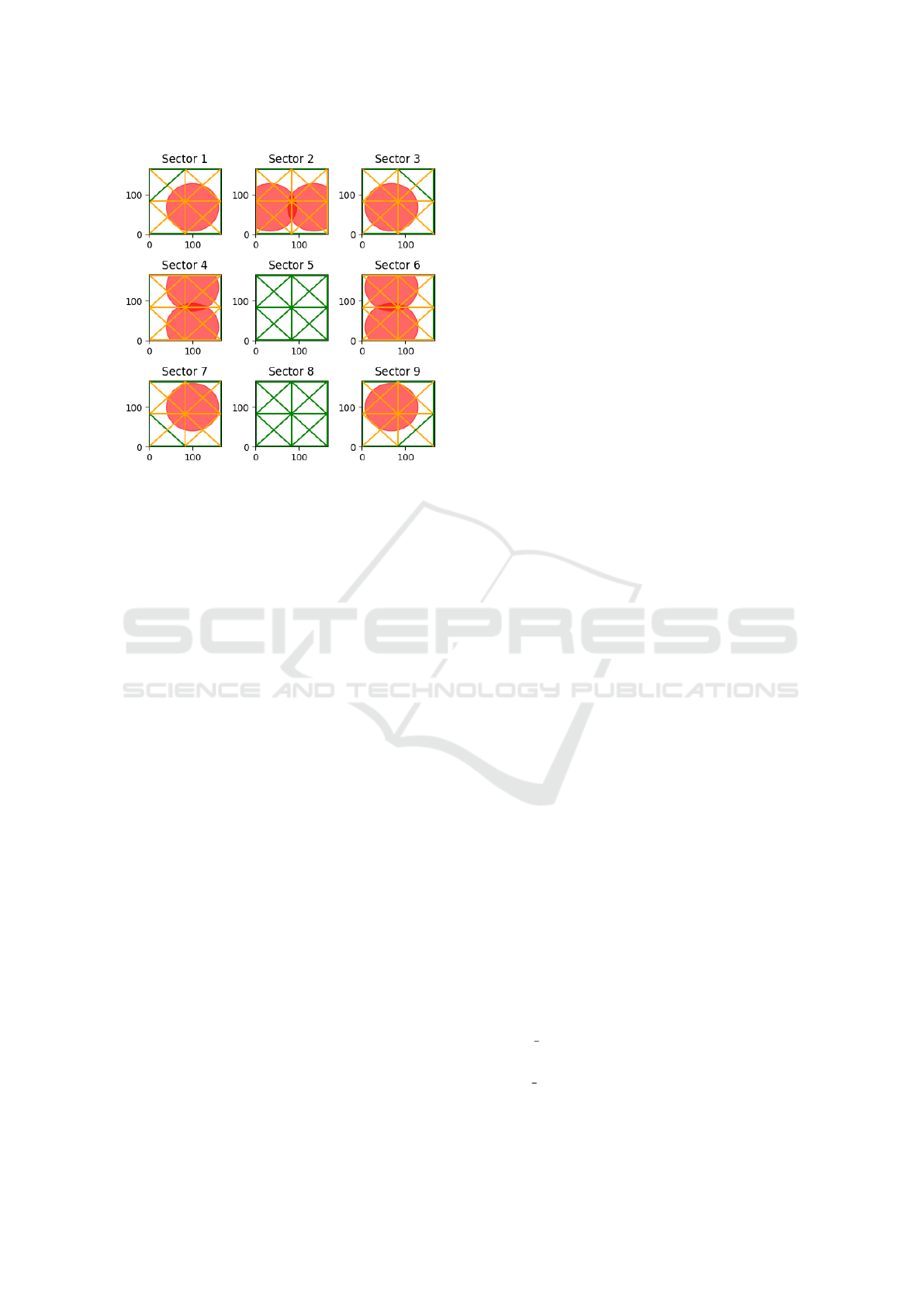
Figure 4: Testing sector passability.

path has at least one passable route in each sec-

tor. The probability of passage through the path is

calculated.

8. Selection of passable routes. We eliminate all

paths from the list that contain at least one sector

deemed impassable.

9. Classiﬁcation of routes, data discretization, and

selection of the best route using the designed clas-

siﬁer. We create a table of passable routes and

then apply discretization (according to a set of

rules) to select the best route according to the de-

cision matrix.

10. Extraction of route points. From the selected best

route, we record the points belonging to the route

sectors into a new array.

11. Implementation of the potential ﬁeld algorithm.

We overlay the ﬁltered map with a table of points

to maximize the chances of passage.

12. Generating the optimal route using the potential

ﬁeld algorithm, maintaining ﬂexibility within safe

sectors.

13. Apply the path smoothing algorithm by taking

into account 3 points in order.

In the next section, we will discuss the main at-

tributes that make up the path vector. The elements

discussed and the way they are classiﬁed is crucial for

the proper functioning of the algorithm.

6 PATH SELECTION SYSTEM

BASED

This section will discuss the decision-making mecha-

nisms used in the presented algorithm.

6.1 Choosing Proper Sectors for

Finding the Optimal Path

A decision-making system was employed to select

the optimal path among the vectors of paths contain-

ing various attributes. This approach allowed for the

development of an efﬁcient decision-making mecha-

nism in situations where multiple paths meet the ba-

sic drivability condition. The primary condition for

path drivability is the presence of probabilistic con-

ditions allowing for passage between obstacles. If a

path in even one of the sectors on the planned route

contains a set of obstacles that prevent direct passage,

it is considered impassable (see ﬁg. 4). When a path is

deemed passable, the probability of a successful pas-

sage is determined. The higher the probability, the

better the quality assessment of the path. The chance

of passability is one of the key attributes used in as-

sessing the quality of the path.

The decision-making mechanism used in the al-

gorithm employs Hamming distances (Waggener and

Waggener, 1995), (Hamming, 1950). Since the input

data metrics in vectors are numerical, there is a need

to discretize them. The data discretization process

was conducted according to specially deﬁned formu-

las and rules for the algorithm, which establish thresh-

olds for determining binary values.

6.2 Data Preparation

In the current subsection, we will focus on the steps

responsible for data preparation and the rules applied

to prepare data for computation through discretiza-

tion.

Example data preparation (path vector discretiza-

tion):

[1, 0.5, 5, 438, 5] → [Yes, High, Low, High, Low].

The attribute names of the above vector (accord-

ing to the order of elements in the vector) are as fol-

lows:

• road pass → value from 0 to 1, discrete value:

No or Yes,

• pass probability → value from 0 to 1, where 1

is 100% pass probability, discrete value: Low or

High,

CSEDU 2025 - 17th International Conference on Computer Supported Education

152

• path length → counted in the number of sectors,

discrete value: Low or High,

• points on path → number of mereological points

on the path, discrete value: Low or High,

• obstacles on path → number of obstacles on the

path, discrete value: Low or High.

Next, we will discuss step by step how to dis-

cretize any vector.

6.2.1 Data Discretization

The data discretization process is a key element of the

presented algorithm and plays a crucial role in prepar-

ing data. Given the application of Hamming measures

in the decision-making model, it is essential to pro-

cess the data in such a way that numerical attributes

are converted into binary values. Special formulas

and rules have been developed for each attribute that

requires discretization. These rules deﬁne thresholds

that allow the transformation of numerical attributes

into binary decision values. Below, the applied for-

mulas are described in detail, and speciﬁc threshold

values are indicated, which are necessary for the algo-

rithm to perform calculations correctly. These formu-

las have been adapted to the speciﬁcs of the data and

the nature of the problem the algorithm is intended to

solve, thereby ensuring it is efﬁcient and effective.

Discretization of the Number of Points on the

Path T

The following formula T

× l is used to calculate

the threshold indicator (average) expected number of

points that should be found on a path of a given length

l. Where T

is a Threshold Number Of Points, p rep-

resents the total number of points on the map, n is a

number of sectors calculated as rows × cols and l is

the length of the path.

For the attribute of the examined path to be clas-

siﬁed as ’yes’, the actual number of potential ﬁeld

points on the examined path must be greater than the

value T

. If the number of points is less than the value

, the attribute is marked as ’no’.

In the next step of the discretization process, we

will perform discretization of the path length.

Discretization of the Path Length T

Determining whether a path is short (yes) or long (no)

is an essential attribute for making a good choice of

the optimal route. The optimal length of the path is

related to the number of sectors on the map. It is as-

sumed that paths no longer than the route along the

outer edges are considered quick to traverse (yes).

The threshold value of the path length is determined

by the following formula T

= r + c. Where T

is the

Threshold Path Length, r is the number of rows in the

grid, and c is the number of columns in the grid.

Remark. It should be noted that the exact thresh-

old value of the path length is r + c − 1; however, to

provide a larger buffer for routes and to avoid a situa-

tion where the path length is too dominant a factor, it

is better to use a threshold length equal to r + c.

Discretization of the Number of Obstacles on the

Path T

The threshold indicator T

× l, similar to the pre-

viously discussed threshold indicator of points T

is used to calculate the threshold (average) expected

number of obstacles that should be present on a path

of a given length l.

Where T

is the Threshold Number Of Obstacles,

o is the total number of obstacles, n is computed as

rows × cols and l refers to the length of the path. For

the attribute of the examined route to be classiﬁed as

’yes’, the actual number of obstacles on the examined

path must be less than the value T

. If the number of

obstacles is greater than the value T

, the attribute is

marked as ’no’.

Next, we have to discuss the last, and one of the

most important indicators of the route, which deﬁnes

the probability of the passage of the route.

Discretization the Probability of Passage T

The discretization of the probability of passage at-

tribute T

was determined experimentally. The op-

timal threshold coefﬁcient was set at T

= 0.35. This

value is related to the probability of passage and can

be interpreted as total freedom of movement on a

passable route. An actual value above 0.35 means that

more than 35% of all possible movements in sectors

(vertical, horizontal, and diagonal movements) of the

route are possible. The higher the indicator value, the

better the situation, hence if the attribute takes on a

value greater than 0.35, we consider it as ’yes’; val-

ues below this threshold are considered as ’no’.

6.3 Route Vector Similarity

Comparison

After performing the path discretization, we proceed

to check the degree of membership of the discretized

path vector concerning the learning matrix α (see tab.

1). For this purpose, we use the classiﬁer, designed to

make decisions in the selection of the optimal path.

The classiﬁer uses Hamming distances to calculate

the similarity between sets of attributes. Then, it

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application

153

performs upper and lower approximation calculations

and determines boundary values. Using the deter-

mined approximations and boundary values, a clas-

siﬁcation of the input attribute sets (path vectors) is

performed. Classiﬁcation consists of ﬁnding the at-

tribute set in the α matrix that is most similar based

on Hamming distances. For new attribute sets entered

for classiﬁcation, a decision from the α learning ma-

trix is assigned. The vector that shows the highest de-

gree of similarity to the ’yes’ decision is selected for

ﬁnal use. When two vectors or more have the same

degree of similarity to the ’yes’ decision, the lowest

value of the degree of similarity to the ’no’ decision

decides the selection.

6.4 Using Learning Matrix α

The decision-making system utilizes a deﬁned deci-

sion matrix α. This matrix contains rules that deter-

mine the quality level of each path. The quality level

of a path is deﬁned as the degree of membership of

the path vector to the most optimal solution (vector)

speciﬁed in the matrix α (see tab. 1). Decision vectors

marked as ’yes’ are considered the most desirable in

evaluating the path quality. The more a path attribute

vector resembles the optimal vector deﬁned in matrix

α, the better it is considered in terms of quality com-

pared to other less similar vectors. Conversely, vec-

tors in matrix α marked as ’no’ are regarded as the

least desirable.

In the table below, the row with bold attributes

presents a sample decision for the path vector solved

using the PPOM method (see ﬁg. 5):

[7, [7, 8, 9, 6, 3], 1, 0.4833333333333333, 5, 449, 5]

Next, the vector needs to be prepared for the

decision-making process. To do this, we omit the ﬁrst

three attributes that are not required in the decision-

making process but are used to store information

about the path (Path ID, Path sectors, and Passabil-

ity). To make a decision, the Passability attribute

must be 1 (meaning that the path has a probabilistic

chance of being passable). The following attributes

remain pass probability, path length, points on path,

obstacles on path. For the presented example, we

create a shortened vector:

[0.4833333333333333, 5, 449, 5]

Now we discretize it according to the rules

described in the previous chapter and obtain the

vector:

[’High’, ’Low’, ’High’, ’Low’]

Next, we search the decision table α for the deci-

sion most similar to the analyzed vector.

Table 1: Learning Matrix α.

Pass probability Path length Points on path Obstacles on path Decision

High Low High Low yes

High Low Low Low yes

High Low Low High yes

High Low High High yes

High Low High High no

Low High Low Low no

Low High High High no

Low High Low High no

The learning matrix α was developed based on

experiments and achieved the best results in the

decision-making process of choosing the optimal

route.

In the next section, we will analyze several cases

of maps with obstacles that posed challenges for the

basic version of the algorithm. We will then compare

these cases with solutions generated by the improved

version of the potential ﬁelds algorithm.

7 ANALYSIS OF RESULTS

The results of the presented algorithm have been

demonstrated through the comparison of several re-

peatable critical scenarios, simulating situations that

telemedicine robots may encounter in real-world en-

vironments, such as hospitals or patients’ homes.

These scenarios are designed not only to evaluate the

algorithm’s efﬁciency but also to serve as educational

case studies for training purposes. The basic potential

ﬁeld algorithm, known for its limitations in complex

environments, is contrasted with the improved ver-

sion, with the comparison structured as follows: the

basic algorithm is presented on the left side (critical

solution), and the improved algorithm – on the right

side.

As observed in the ﬁgures below (ﬁg. 5), the crit-

ical scenarios involve situations such as navigating

through ’narrow passages’ or areas densely populated

with obstacles. These are particularly challenging due

to the limited number of potential ﬁeld points in such

spaces. When the basic algorithm encounters an im-

passable obstacle, it often fails to recover by turning

back or ﬁnding an alternative path, leading to com-

plete route blockage.

In contrast, the improved algorithm employing

preprocesses the environment map to identify and

exclude areas with a high likelihood of obstruction.

This preprocessing step provides an opportunity for

learners to understand how predictive analysis and

preprocessing can signiﬁcantly enhance the perfor-

mance of robotic systems. By directing the robot

CSEDU 2025 - 17th International Conference on Computer Supported Education

154

through passable sectors identiﬁed during preprocess-

ing, the improved algorithm ensures successful navi-

gation through previously impassable scenarios.

These ﬁndings not only highlight the practical ad-

vantages of the enhanced method but also demon-

strate its pedagogical value in training students and

professionals. The ability to visualize and analyze

these critical cases fosters a deeper understanding

of robotic navigation challenges and equips learners

with the skills needed to address similar issues in di-

verse environments. By simulating such scenarios,

the framework provides a unique opportunity to com-

bine theoretical knowledge with hands-on problem-

solving experience.

(a) Case 1: critical solution

(b) Case 1: PPOM solution

Figure 5: Case 1: critical problem and PPOM solution.

In a further 9 case studies performed on maps with

a different conﬁguration of obstacles and points, the

algorithm solved the passability problem and planned

the path correctly.

8 ALGORITHM COMPLEXITY

Path Planning Optimization Method (PPOM) is an ad-

vanced combination of two methodologies, integrat-

ing heuristic approaches for efﬁcient path planning

in obstacle environments. This algorithm, through

its complex structure of operation, aims to overcome

the limitations of classical heuristic methods, which

in the case of an unfavorable obstacle conﬁguration

can fall into the so-called ”local traps”, while requir-

ing a signiﬁcant number of computations to ﬁnd the

optimal path to the goal. In response to these chal-

lenges, PPOM implements a two-step approach: the

ﬁrst module of the algorithm selects key sectors of

space that maximize the probability of ﬁnding the

optimal path, while the second module uses greedy

heuristic algorithms to choose the best local solution

in a previously deﬁned space.

The ﬁrst component of the algorithm acts as a

high-level selector, selecting the main sectors of space

based on the probability of minimizing interactions

with obstacles that could prevent further route search.

The number of possible paths in this part of the algo-

rithm is constant and equal to C = 235 (for dividing

the map into a 3x3 grid of sectors). This means that

the computational complexity of this phase is O(1),

which implies a constant computational complexity,

independent of the size of the input data.

The second component of the algorithm is respon-

sible for precise route determination using potential

ﬁelds that model the map space. The complexity of

this part of the algorithm is determined by the num-

ber of points in the potential ﬁeld space. The number

of steps in this stage is proportional to the number of

points on the map, which leads to a linear complex-

ity of O(N), where N is the number of potential ﬁeld

points.

Considering both stages of the algorithm’s opera-

tion, its overall computational complexity

is O(C * N), which indicates a linear dependence on

the number of points in the potential space.

It should be emphasized that the given complex-

ity refers to cases with the highest level of complex-

ity. In typical conditions, the computational complex-

ity of the algorithm is much more efﬁcient, which is

beneﬁcial in the context of a wide range of applica-

tions. Unlike classical path ﬁnding algorithms, which

do not take into account the aspect of route passability

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application

155

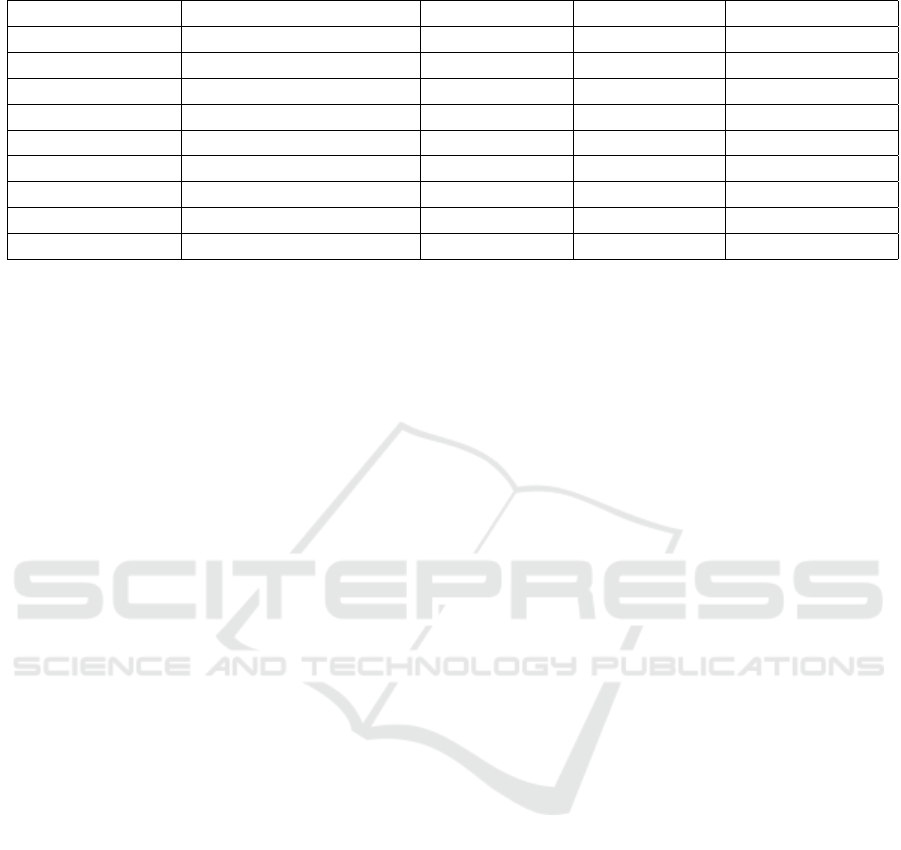
Table 2: Comparison of PPOM Algorithm with Other Pathﬁnding Algorithms.

Algorithm Computational Complexity Complexity Type Is PPOM faster? Paper Reference

PPOM O(C · N) Linear - -

A* O(b

) Exponential Yes (Hart et al., 1968)

Dijkstra O(E · logV + E +V · logV ) Polynomial Yes (Dijkstra, 1959)

BFS O(|V | + |E|) Linear No (Moore, 1959)

DFS O(|V | + |E|) Linear No (Tarjan, 1972)

Bellman-Ford O(|V | · |E|) Polynomial Yes (Bellman, 1958)

Johnson’s Algorithm O(|V |

log|V | + |V ||E|) Polynomial Yes (Johnson, 1977)

Floyd-Warshall O(|V |

) Polynomial Yes (Floyd, 1962)

IDA* O(b

) Exponential Yes (Korf, 1985)

in the face of obstacles, PPOM effectively copes with

this issue. In traditional algorithms, graphs contain-

ing obstacles generate decision nodes that can lead

to situations in which it is impossible to continue the

path search. PPOM eliminates this risk through intel-

ligent selection of sectors, minimizing the probability

of problematic decision nodes, which signiﬁcantly in-

creases the efﬁciency and computational optimization

in environments with obstacles.

9 CONCLUSIONS

As a result of this research, a new algorithm has

been developed to enhance the performance of basic

path planning methods in environments with numer-

ous obstacles using potential ﬁelds. This improved

algorithm reduces the likelihood of paths leading into

’traps,’ which are typically closed areas with narrow

entrances. It incorporates a decision-making system

allowing for the selection of the most likely successful

path for a robot. Furthermore, it minimizes unneces-

sary wandering during path planning, which is partic-

ularly beneﬁcial for large maps containing labyrinth-

like structures with dead ends.

The effectiveness of the improved algorithm was

assessed using 10 different critical scenarios, repre-

senting typical challenges of navigating ’narrow pas-

sages’ that lead to impassable routes. In 8 out of the

10 cases, the algorithm successfully identiﬁed a vi-

able path. The tests utilized a division of the map

into a 3x3 grid (3 columns and 3 rows), which proved

to be an optimal conﬁguration relative to the obstacle

sizes used in the experiments. For environments with

signiﬁcantly smaller obstacles, a larger grid division,

such as 4x4, is suggested. It is also recommended that

the division of the map be as symmetrical as possible,

with sector sizes close to square shapes to ensure uni-

form coverage.

However, increasing the map division size raises

the computational complexity, as the number of po-

tential paths grows signiﬁcantly. It is therefore ad-

vised to determine the optimal grid size experimen-

tally, balancing computational efﬁciency with naviga-

tional precision.

This study achieved its objective by demonstrat-

ing the effectiveness of the proposed algorithms in

addressing complex navigational challenges. The re-

sults conﬁrm that the algorithm excels in environ-

ments with intricate layouts, such as hospital wards

or patient residences resembling mazes. The gener-

ated paths ensure precise navigation while effectively

avoiding obstacles, making the system well-suited for

telemedicine applications.

Future applications of the PPOM algorithm in-

clude its integration into telemedical robots for prac-

tical use in real-world settings. These robots will

navigate hospital spaces while considering the phys-

ical layout of obstacles, such as medical equipment

in rooms. Furthermore, they will be equipped to ac-

tively and directly interact with patients, providing an

educational tool for training operators and students

in navigating complex environments with robotic sys-

tems.

Additionally, we plan to further improve the algo-

rithm and test it in the task of avoiding obstacles in

the form of rock mazes, simulating the movement of

a ground drone in desert conditions on Mars.

ACKNOWLEDGEMENTS

This work has been supported by a grant from the

Ministry of Science and Higher Education of the Re-

public of Poland under project number 23.610.007-

110 and a grant from the National Centre for Re-

search and Development in Poland, grant number:

POIR.01.01.01-00-0587/21 Development of telemed-

ical software for conducting automated subjective pa-

tient examination and enabling preliminary medical

diagnosis based on AI.

CSEDU 2025 - 17th International Conference on Computer Supported Education

156

REFERENCES

Bellman, R. (1958). On a routing problem. Quarterly of

Applied Mathematics, 16(1):87–90.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1:269–271.

Falcione, S., Campbell, E., McCollum, B., Chamberlain, J.,

Macias, M., Morsch, L., and Pinder, C. (2019). Emer-

gence of different perspectives of success in collabo-

rative learning. Canadian Journal for the Scholarship

of Teaching and Learning, 10(2):n2.

Floyd, R. W. (1962). Algorithm 97: Shortest path. Commu-

nications of the ACM, 5(6):345.

Gny

s, P. (2017). Mereogeometry based approach for be-

havioral robotics. In Rough Sets: International Joint

Conference, IJCRS 2017, Olsztyn, Poland, July 3–7,

2017, Proceedings, Part II, pages 70–80. Springer.

Hamming, R. W. (1950). Error detecting and error cor-

recting codes. The Bell system technical journal,

29(2):147–160.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, 4(2):100–107.

Johnson, D. B. (1977). Efﬁcient algorithms for short-

est paths in sparse networks. Journal of the ACM,

24(1):1–13.

Komorowski, J., Pawlak, Z., Polkowski, L., and Skowron,

A. (1999). Rough sets: A tutorial. Rough fuzzy hy-

bridization: A new trend in decision-making, pages

3–98.

Korf, R. E. (1985). Depth-ﬁrst iterative-deepening: An op-

timal admissible tree search. Artiﬁcial Intelligence,

27(1):97–109.

Moore, E. F. (1959). The shortest path through a maze. Pro-

ceedings of the International Symposium on the The-

ory of Switching, pages 285–292.

Nurdin, S. and Setiawan, W. (2016). Improving students’

cognitive abilities and creative thinking skills on tem-

perature and heat concepts through an exelearning-

assisted problem based learning. International Jour-

nal of Scientiﬁc & Technology Research, 5(12):59–63.

Osmialowski, P. (2011). Planning and navigation for mobile

autonomous robots spatial reasoning in player. Stage

System.

smiałowski, P. and Polkowski, L. (2010). Spatial reason-

ing based on rough mereology: a notion of a robot for-

mation and path planning problem for formations of

mobile autonomous robots. In Transactions on rough

sets XII, pages 143–169.

Othman, M. and Zaın, N. (2015). Online collaboration

for programming: Assessing students’ cognitive abil-

ities. Turkish Online Journal of Distance Education,

16(4):84–97.

Pawlak, Z. (1992). Rough sets: Theoretical aspects of rea-

soning about data.

Planas-Llad

o, A., Feliu, L., Arbat, G., Pujol, J., Su

nol, J. J.,

Castro, F., and Mart

ı, C. (2021). An analysis of team-

work based on self and peer evaluation in higher edu-

cation. Assessment and Evaluation in Higher Educa-

tion, 46(2):191–207.

Polkowski, L. and O

smiałowski, P. (2008). A framework for

multiagent mobile robotics: Spatial reasoning based

on rough mereology in player/stage system. In Chan,

C.-C., Grzymala-Busse, J. W., and Ziarko, W. P., ed-

itors, Rough Sets and Current Trends in Computing,

pages 142–149, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Polkowski, L. and O

smiałowski, P. (2008). A framework for

multiagent mobile robotics: Spatial reasoning based

on rough mereology in player/stage system. In Rough

Sets and Current Trends in Computing: 6th Inter-

national Conference, RSCTC 2008 Akron, OH, USA,

October 23-25, 2008 Proceedings 6, pages 142–149.

Springer.

Polkowski, L. and Skowron, A. (1996). Rough mereology:

A new paradigm for approximate reasoning. Interna-

tional Journal of Approximate Reasoning, 15(4):333–

365.

Polkowski, L., Zmudzinski, L., and Artiemjew, P. (2018).

Robot navigation and path planning by means of

rough mereology. In 2018 Second IEEE International

Conference on Robotic Computing (IRC), pages 363–

368. IEEE.

Szpakowska, A., Artiemjew, P., and Cybowski, W. (2023).

Navigational strategies for mobile robots using rough

mereological potential ﬁelds and weighted distance to

goal. In International Joint Conference on Rough Sets,

pages 549–564. Springer.

Tarjan, R. E. (1972). Depth-ﬁrst search and linear graph

algorithms. SIAM Journal on Computing, 1(2):146–

160.

Taxirovna, A. S. (2024). Collaborative learning: Fo-

cusing on techniques that promote teamwork and

shared knowledge among students. SO ‘NGI ILMIY

TADQIQOTLAR NAZARIYASI, 7(1):118–123.

Waggener, B. and Waggener, W. N. (1995). Pulse code

modulation techniques. Springer Science & Business

Media.

Zmudzinski, L. and Artiemjew, P. (2017). Path planning

based on potential ﬁelds from rough mereology. In

Rough Sets: International Joint Conference, IJCRS

2017, Olsztyn, Poland, July 3–7, 2017, Proceedings,

Part II, pages 158–168. Springer.

Training Telemedicine Robots: A Path Planning Optimization Method for Educational and Medical Application

157