Quantum Convolutional Neural Networks for Image Classification:
Perspectives and Challenges
Fabio Napoli
1 a
, Lelio Campanile
1 b
, Giovanni De Gregorio
1,2 c
and Stefano Marrone
1 d
1
Dipartimento di Matematica e Fisica, Universit
`
a degli Studi della Campania “Luigi Vanvitelli”,
viale Lincoln 5, Caserta, Italy
2
Istituto Nazionale di Fisica Nucleare, Complesso Universitario di Monte S. Angelo, Via Cintia, Napoli, I-80126, Italy
Keywords:
Quantum Convolutional Neural Networks, Labelled Faces in the Wild, Face Recognition.
Abstract:
Quantum Computing is becoming a central point of discussion in both academic and industrial communities.
Quantum Machine Learning is one of the most promising subfields of this technology, in particular for image
classification. In this paper, the model of Quantum Convolutional Neural Networks and some related imple-
mentations are explored in their potential for a non-trivial task of image classification. The paper presents
some experimentations and discusses the limitations and the strengths of these approaches when compared
with classical Convolutional Neural Networks. Furthermore, an analysis of the impact of the noise level on
the quality of the classification task has been performed. This paper reports a substantial equivalence of the
perfomance of the model with respect the level of noise.
1 INTRODUCTION
Machine Learning (ML) has become a powerful tool
for pattern recognition, enabling Artificial Intelli-
gence (AI) diffusion. Transformer-based models ex-
emplify its capabilities, enabling human-like text gen-
eration and natural language processing. Meanwhile,
the volume of stored data grows exponentially, ex-
ceeding several hundred exabytes and increasing at
20% annually (Hilbert and L
´
opez, 2011). This surge
has spurred interest in novel ML approaches capa-
ble of managing and extracting insights from vast
datasets, with Quantum Computing (QC) emerging as
a promising frontier (Schuld and Petruccione, 2021).
By leveraging superposition and entanglement,
QC offers new paradigms for optimization, image
processing, and complex data analysis, promising sig-
nificant speed-ups over classical methods. However,
realizing Quantum Machine Learning (QML)’s full
potential requires overcoming key challenges, includ-
ing quantum noise, scalability, and integration with
classical models. Noisy Intermediate-Scale Quan-
tums (NISQs) devices introduce decoherence and gate
a
https://orcid.org/0009-0001-0396-7968
b
https://orcid.org/0000-0003-4021-4137
c
https://orcid.org/0000-0003-0253-915X
d
https://orcid.org/0000-0003-1927-6173
errors, complicating reliable computation. Conse-
quently, many algorithms are tested in simulated en-
vironments, where classical resources approximate
quantum behaviour, enabling stability analysis and
performance comparisons with other ML approaches.
This study investigates Quantum Convolutional
Neural Networks (QCNNs) for image classification,
evaluating their performance in both ideal and noisy
simulated environments. The impact of quantum
noise on model accuracy is analyzed to assess the
feasibility of QCNNs in practical scenarios. Experi-
mental results highlight both the potential and the cur-
rent limitations of QCNNs, emphasizing the gap be-
tween quantum advantage and existing hardware con-
straints.
The paper is structured as follows: Section 2 re-
ports a review of the relevant papers; Section 3 de-
scribes the foundation of the work and the followed
methodology; Section 4 describes the experimenta-
tions carried on in the work and discusses the main
results; Section 6 ends the paper and draws conclu-
sions.
2 RELATED WORK
Recent studies explore various QML and Deep
Learning (DL) architectures for image classifica-
Napoli, F., Campanile, L., De Gregorio, G. and Marrone, S.
Quantum Convolutional Neural Networks for Image Classification: Perspectives and Challenges.
DOI: 10.5220/0013521500003944
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Internet of Things, Big Data and Security (IoTBDS 2025), pages 509-516
ISBN: 978-989-758-750-4; ISSN: 2184-4976
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
509

tion (Kharsa et al., 2023), including Quantum Sup-
port Vector Machines (QSVM), Quantum K-Nearest
Neighbors (Q-KNNs), QCNNs, Variational Quan-
tum Circuits (VQCs), and Quantum Tensor Net-
works (QTNs). These works highlight the promise
of QC while acknowledging the limitations imposed
by NISQs devices and the need for improved quantum
image encoding and larger datasets.
The study in (Lu et al., 2021) presents a QCNN
model applied to Modified National Institute of Stan-
dards and Technology (MNIST), leveraging hierar-
chical quantum layers inspired by classical Convo-
lutional Neural Networks (CNNs). Using ampli-
tude encoding and approximate state preparation, the
model optimizes qubit usage, demonstrating its ef-
fectiveness in digit classification. Similarly, (Chen
et al., 2023) investigates how different image types
affect QCNN performance, emphasizing quantum ini-
tial state preparation and exploring two local feature
construction schemes, Scale Layer Unitary Circuits
(SLUCs) and Box-Counting Based Fractal Features
(BCBFFs). The study examines how QCNNs inte-
grate local features into a global circuit, assessing
their adaptability for classical image classification.
In (Easom-Mccaldin et al., 2024), a single-qubit-
based deep Quantum Neural Network (QNN) is pro-
posed to improve parameter efficiency and scalability
in high-dimensional image classification tasks. The
authors examine VQCs expressibility, entanglement
capabilities, and noise resilience, identifying a satu-
ration point where increased circuit depth no longer
improves classification accuracy. While dataset de-
tails are not specified, the study likely includes bench-
marks like MNIST.
The research in (Hassan et al., 2024) applies a
hybrid QCNN-Residual Neural Network (ResNet) ar-
chitecture to the MNIST Medical dataset, integrating
a quantum component for preprocessing and feature
extraction while leveraging a pre-trained ResNet for
classification. With an accuracy of 99.7%, this hy-
brid model outperforms standalone QCNNs and clas-
sical ResNet, demonstrating the benefits of quantum-
classical integration.
The paper (Gong et al., 2024) focuses on bi-
nary classification tasks without specifying a partic-
ular dataset. The study explores parameter adjust-
ments and uniform normalization techniques to miti-
gate data representation distortions, highlighting pre-
processing strategies for optimized quantum compu-
tation. The proposed QCNN architecture is based
on VQCs and follows a standard QCNN structure,
including data encoding, convolutional layers, and
pooling layers, but omitting a fully connected layer
to align with the binary classification objective. The
paper investigates different convolutional kernel cir-
cuits, including Tree Tensor Networks (TTNs) (Wall
and D’Aguanno, 2021) and SU(4) circuit (Lazzarin
et al., 2022), to enhance model training. While spe-
cific performance metrics are not provided, the study
centres on circuit design optimizations and their im-
plications for classification accuracy.
The research in (Sebastianelli et al., 2022) ap-
plies a hybrid quantum-classical CNN to the Eu-
roSAT dataset, consisting of Sentinel-2 satellite im-
ages across 13 spectral bands and ten land-use cate-
gories. A quantum layer is integrated into a modi-
fied LeNet-5 architecture, comparing different circuit
configurations against classical models. The results
indicate that hybrid QCNNs achieve superior classi-
fication accuracy, particularly when incorporating en-
tanglement.
A hybrid classical-quantum transfer learning
model is introduced in (Zhang et al., 2023), combin-
ing a ResNet network for feature extraction with a
tensor quantum circuit to fine-tune parameters on the
RSI dataset. The study demonstrates improved clas-
sification accuracy and reduced parameter require-
ments compared to conventional CNN-based Remote
Sensing Image Scene Classification (RSISC) meth-
ods, particularly for small datasets.
The study in (Oh et al., 2021) integrates Quantum
Random Access Memory (QRAM) to efficiently load
classical image data into quantum states, using quan-
tum convolutional layers to perform feature extraction
akin to classical CNNs. While performance details
are not explicitly stated, the study suggests advan-
tages in memory efficiency and computational speed.
Lastly, (Huang et al., 2023) proposes a hybrid Hy-
brid Quantum-Classical Convolutional Neural Net-
work (HQ-CNN) model, integrating quantum convo-
lutional layers with classical neural networks. He
utilizes the MNIST dataset, albeit with a reduced-
dimensionality subset due to the computational con-
straints of quantum simulations. The approach lever-
ages parameterized VQCs as quantum convolutional
filters, improving feature extraction and robustness
against adversarial attacks. Evaluations against Fast
Gradient Sign Method (FGSM) and Random Plus
FGSM attacks show that HQ-CNNs maintain higher
classification accuracy and exhibit slower accuracy
degradation than classical CNNs, emphasizing the re-
silience of quantum kernels in adversarial scenarios.
3 METHODOLOGY
We implemented and evaluated QCNNs for image
classification using a pipeline that includes data pro-
AI4EIoT 2025 - Special Session on Artificial Intelligence for Emerging IoT Systems: Open Challenges and Novel Perspectives
510

cessing, quantum encoding, convolutional layer de-
sign, and noise integration to simulate quantum hard-
ware limitations.
The Labelled Faces in the Wild (LFW) dataset
(Huang et al., 2008)—comprising grayscale face im-
ages—was reduced to a binary classification prob-
lem (distinguishing “Colin Powell” from “George W.
Bush”) with at least 200 images per class; pixel values
were normalized to the range [0, 1]
To address hardware constraints, dimensionality
reduction was performed using Principal Component
Analysis (PCA) to project the data onto a lower-
dimensional space with minimal information loss, as
described by Eq. 1.
X
PCA
= X ·W
PCA
, (1)
Classical data is then encoded into quantum states
via angle embedding, where each input vector is
mapped through X-axis rotations (Eq. 2).
|ψ⟩ =
d
∏
i=1
R
X
(x
i
)|0⟩. (2)
The quantum circuit comprises multiple layers of
parameterized single-qubit rotations and entangling
Controlled NOT (CNOT) gates (Eq. 3), with dropout
implemented via depolarizing channels (Eq. 4) to re-
duce overfitting.
U
layer
(θ) =
d
∏
i=1
CNOT (i,(i + 1) mod d)·
d
∏
i=1
R
Z
(θ
i,1
)R
Y
(θ
i,2
)R
Z
(θ
i,3
), (3)
E
dropout
(ρ) = (1 −p)ρ +
p
2
n
I, (4)
To simulate realistic conditions, depolarizing and
phase damping noise channels (Eqs. 5 and 6) are ap-
plied after each layer.
E
depolarizing
(ρ) = (1 −p)ρ +
p
3
(XρX +Y ρY + ZρZ)
(5)
E
phase damping
(ρ) = (1 −p)ρ + pZρZ (6)
The cost function, combining mean squared error
and L2 regularization (Eq. 7), is minimized using the
Adam optimizer with a decaying learning rate (Eq. 8).
L (θ) =
1
N
N
∑
i=1
(y
i
− f (x
i
;θ))
2
+ λ∥θ∥
2
2
, (7)
η
t
=
η
0
√
t + ε
, (8)
Figures 1 and 2 illustrate the quantum circuit of a
single QCNN layer and the overall network architec-
ture, respectively.
4 EXPERIMENTATION AND
DISCUSSION
This section presents a comparative analysis of QC-
NNs under two experimental conditions: an ideal
noise-free scenario and a realistic noisy environment.
The study is based on a binary classification task de-
rived from the LFW dataset, specifically identifying
images of Colin Powell among a mixed set of his im-
ages and those of other individuals. The experimen-
tal implementation leveraged PennyLane for quantum
computation, Scikit-learn for dataset preprocessing,
and Matplotlib for result visualization. The full ex-
perimental code is available in the provided imple-
mentation details.
To establish a performance baseline, we built a
classical CNN with a level of architectural complex-
ity similar to the QCNN. The CNN consists of three
convolutional layers, a fully connected layer, and a
ReLU output. It was trained with the same dataset
(LFW), preprocessing pipeline, and optimization set-
tings (Adam optimizer, 0.001 learning rate) to ensure
fair comparisons.
The results obtained show that the CNN outper-
forms the QCNN in terms of test accuracy, achieving
a solid 86,82%. This performance gap is widely ex-
pected, given the efficiency and optimization in train-
ing of the classical DL architectures. However, the
QCNNs demonstrate other remarkable characteristics
that will be exploited in the following analysis.
5 QUANTUM OPERATIONS AND
MEASUREMENTS
This section introduces the fundamental quantum op-
erations used in the QCNNs, providing a formal de-
scription of state encoding, parameterized rotations,
entanglement, and measurement.
Classical input vectors x ∈ R
d
are embedded into
quantum states via angle embedding, which applies
single-qubit rotations along the X-axis as follows:
|ψ(x)⟩ =
d
O
i=1
R
X
(x
i
)|0⟩, (9)
Quantum Convolutional Neural Networks for Image Classification: Perspectives and Challenges
511

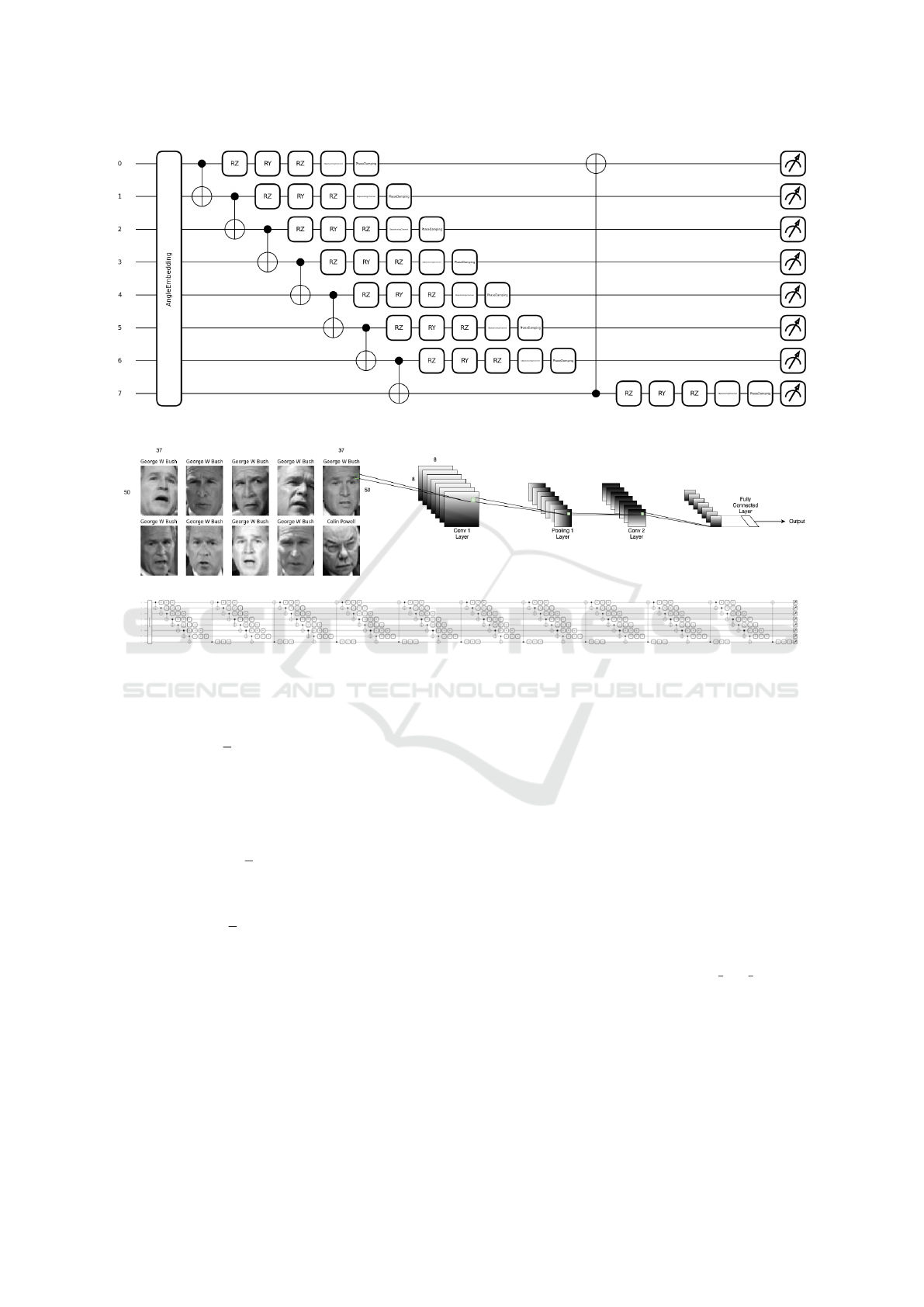
Figure 1: Quantum circuit representation of a single QCNN layer.
Figure 2: Overview of the Quantum Convolutional Neural Network applied to the LFW dataset.
where each feature x
i
sets the rotation angle via the
Pauli-X gate:
R
X
(θ) = exp

−i
θ
2
X

=

cos(θ/2) −isin(θ/2)
−isin(θ/2) cos(θ/2)

.
(10)
Trainable parameters are introduced using single-
qubit rotations along the Z- and Y -axes. The Pauli-Z
rotation is given by:
R
Z
(θ) = exp

−i
θ
2
Z

=

e
−iθ/2
0
0 e
iθ/2

. (11)
The Pauli-Y rotation is expressed as:
R
Y
(θ) = exp

−i
θ
2
Y

=

cos(θ/2) −sin(θ/2)
sin(θ/2) cos(θ/2)

.
(12)
Within the QCNN architecture, each qubit under-
goes a sequence of rotations R
Z
(θ
1
), R
Y
(θ
2
), and
R
Z
(θ
3
) to achieve universal single-qubit operations.
Entanglement is introduced using the CNOT gate,
whose action in the computational basis is:
CNOT =



1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0



. (13)
This gate flips the target qubit’s state when the control
qubit is in |1⟩, establishing correlations among qubits.
Finally, classical information is extracted by mea-
suring the expectation value of the Pauli-Z operator:
⟨Z⟩ = ⟨ψ|Z|ψ⟩, (14)
with the Pauli-Z matrix defined as:
Z =

1 0
0 −1

. (15)
This measurement provides the classical output used
for classification.
5.1 Experimental Framework
The dataset was retrieved using f etch
l f w people()
from Scikit-learn, followed by pixel intensity normal-
ization and transformation into one-dimensional fea-
ture vectors. PCA was applied to reduce dimension-
ality, retaining the top eight principal components,
and the data was subsequently scaled to the range for
quantum embedding. The dataset was divided into
training (60%) and testing (40%) subsets, while pre-
serving class balance.
AI4EIoT 2025 - Special Session on Artificial Intelligence for Emerging IoT Systems: Open Challenges and Novel Perspectives
512

Each 8-dimensional feature vector was encoded
into quantum states via Angle Embedding along the
X-axis. The QCNN structure is implemented in
PennyLane, consisting of ten layers, each contain-
ing trainable single-qubit rotations and followed by
CNOT gates for entanglement. The final circuit mea-
surements were performed using Pauli-Z expectation
values across multiple qubits, yielding the classifica-
tion outcome.
Training was performed using the Adam opti-
mizer, initialized with a learning rate of 0.05. The
loss function combined Mean Squared Error (MSE)
loss with L2 regularization, aiming to prevent overfit-
ting. The training was conducted for five epochs as
an initial assessment and extended to ten epochs for
evaluating long-term convergence trends.
The noise-free scenario was executed on the
de f ault.qubit simulator, ensuring an idealized quan-
tum execution. The noisy setting introduced depolar-
izing noise (probability of 0.01) and phase damping
noise (probability of 0.02) through the de f ault.mixed
backend, simulating real-world quantum errors.
Each layer of the QCNN consists of 40 quantum
gates, calculated as follows. Each qubit undergoes
three parameterized single-qubit rotations, contribut-
ing to 24 gates for 8 qubits. The entangling CNOT
gates contribute another 16 operations, as each qubit
is coupled with its adjacent neighbour in a circular
pattern. The total number of trainable parameters is
240 across all layers, computed as, corresponding to
the three rotation angles per qubit per layer.
If noise is introduced, additional operations are
required to model decoherence effects. Specifically,
Depolarizing and Phase Damping noise channels are
applied after each layer, adding two noise gates per
qubit, resulting in 32 additional operations per layer.
Therefore, the total number of quantum gates per
layer increases from 40 in the noise-free case to 72
in the noisy setting.
The full implementation of the QCNN is available
on GitHub
1
.
5.2 Performance of the Noise-Free
QCNN
The noise-free QCNN demonstrated a training accu-
racy of 79.34% and a test accuracy of 73.21% after
five epochs, showcasing the model’s ability to gener-
alize effectively under ideal conditions. The second
experiment, extending training to ten epochs, resulted
in a training accuracy of 82.45% and a test accuracy of
1
https://github.com/leliocampanile/
IoTBDS-quantumAI
75.62%, highlighting the benefits of additional train-
ing in an idealized setting.
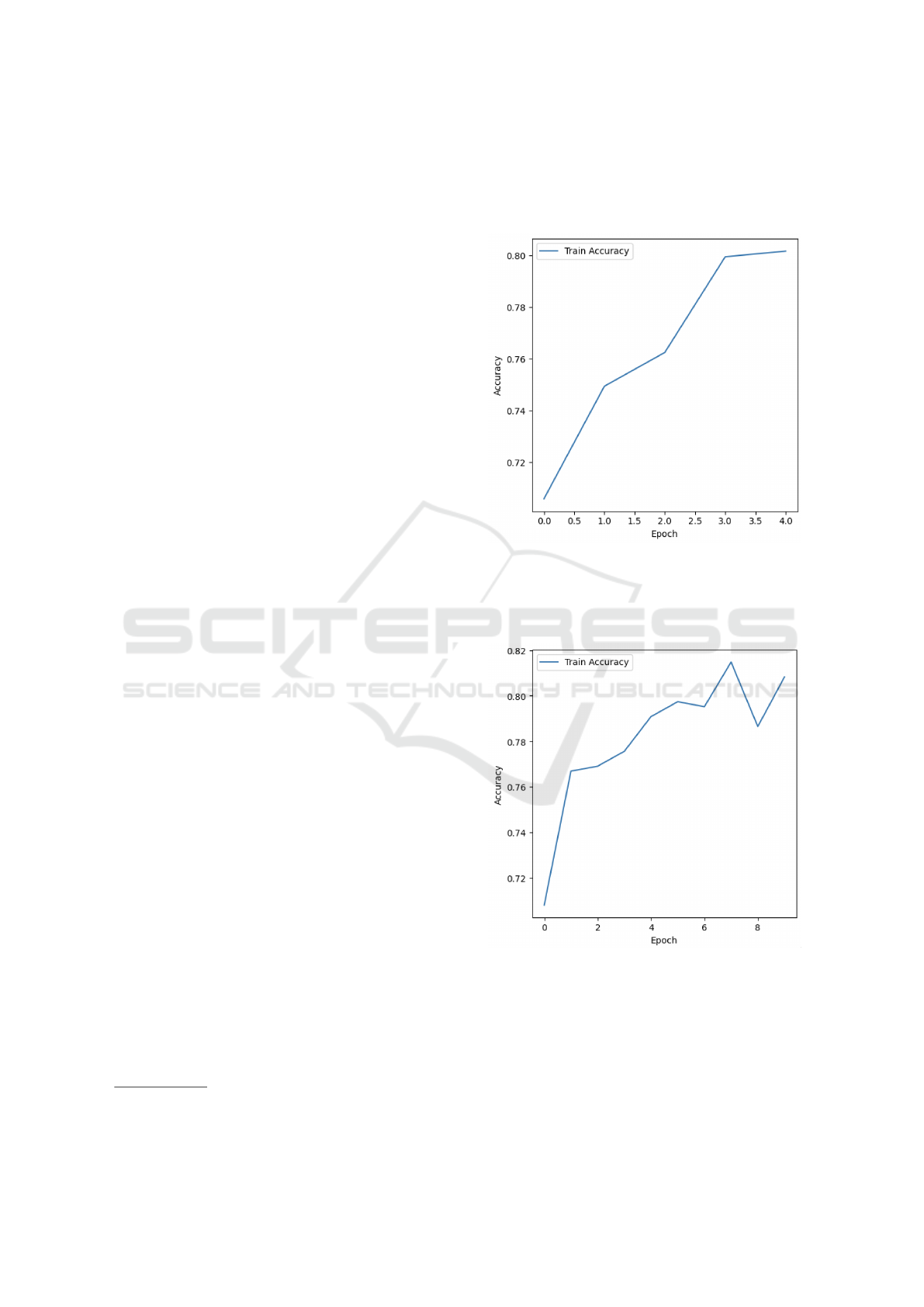
Figure 3 report training accuracy for 5 epochs in
the case of no noise.
Figure 3: Training accuracy for the noise-free QCNN (5
epochs).
Figure 4 report training accuracy for 10 epochs in
the case of no noise.
Figure 4: Training accuracy for the noise-free QCNN (10
epochs).
Table 1 summarises both parameters and perfor-
mance indices for the noise-free QCNN.
Quantum Convolutional Neural Networks for Image Classification: Perspectives and Challenges
513

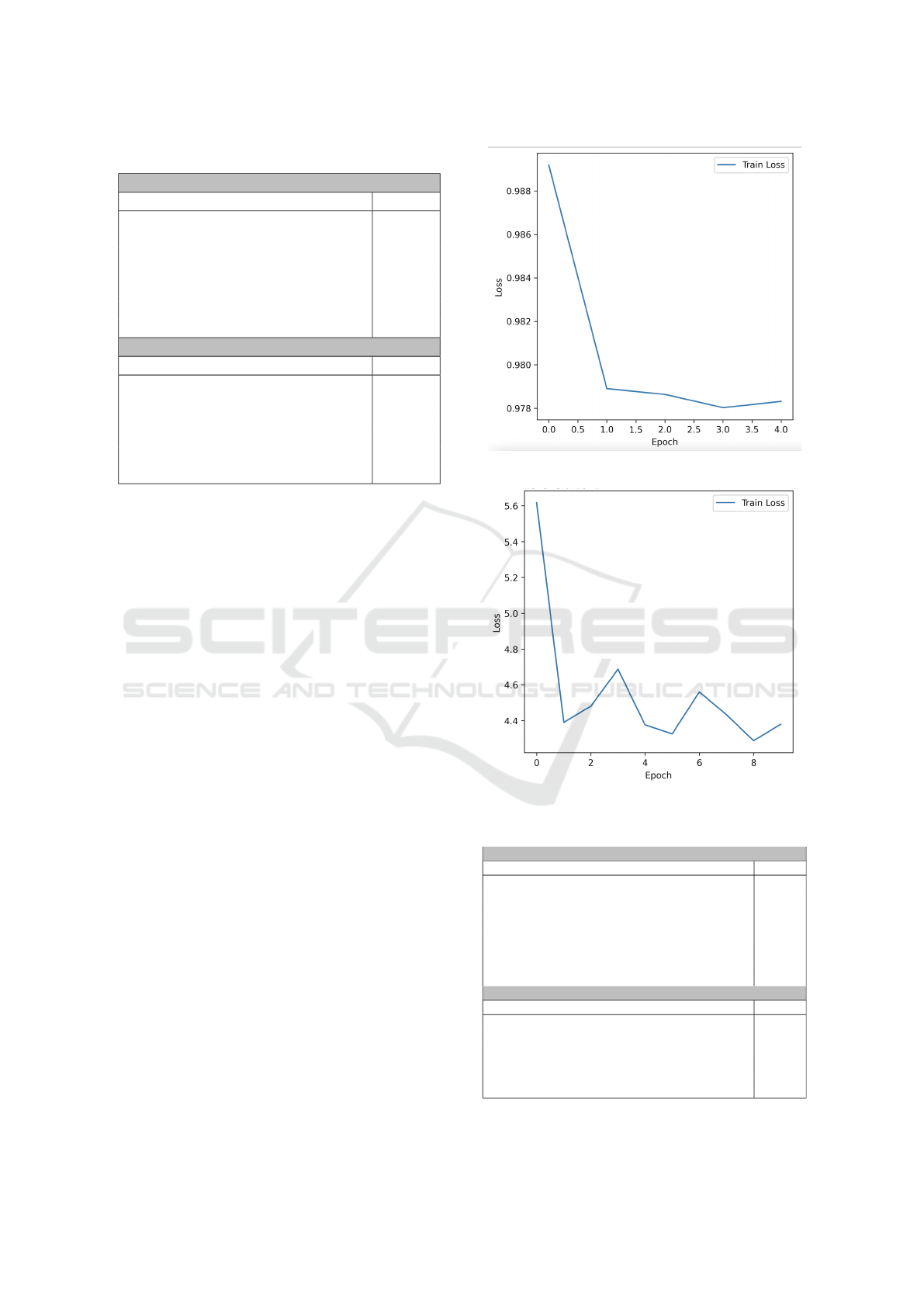
Table 1: Noise-Free QCNN Parameters and Performance.
Parameters
Name Value
Number of Layers 10
Number of Features (PCA) 8
Number of Trainable Parameters 240
Number of Quantum Gates per Layer 40
Optimizer Adam
Learning Rate 0.05
Noise Model None
Indices
Name Value
Training Accuracy (5 Epochs) 79.34%
Test Accuracy (5 Epochs) 73.21%
Training Loss (5 Epochs) 0.16
Training Accuracy (10 Epochs) 82.45%
Test Accuracy (10 Epochs) 75.62%
Training Loss (10 Epochs) 0.15
5.3 Performance of the Noisy QCNN
With the introduction of noise, the QCNN exhibited
a training accuracy of 71.25% and a test accuracy
of 69.45%, reflecting the detrimental effects of deco-
herence and gate errors. In the second experiment,
where the number of training epochs was increased
to ten, the training accuracy decreased to 69.28%
while the test accuracy stagnated at 69.05%. This
suggests that prolonged training under noisy condi-
tions does not yield performance improvements, but
instead leads to an early plateau. The accumulation
of quantum noise disrupts the optimization process,
preventing the model from effectively refining its de-
cision boundary. As noise-induced errors accumulate
over multiple layers and training iterations, they over-
shadow the benefits of longer training, ultimately lim-
iting the network’s learning capacity and reducing its
ability to generalize.
Figure 5 report training loss for 5 epochs in the
case of noise.
Figure 6 report training loss for 10 epochs in the
case of noise.
Table 2 summarises both parameters and perfor-
mance indices for the noisy QCNN.
5.4 Theoretical Runtime Analysis
The noise-free QCNN serves as a benchmark for eval-
uating the theoretical performance of quantum neu-
ral networks. The results confirm that in the absence
of hardware imperfections, QCNNs can achieve ro-
bust classification performance. Conversely, the noisy
variant demonstrates the vulnerability of quantum cir-
Figure 5: Training loss for the noisy QCNN (5 epochs).
Figure 6: Training loss for the noisy QCNN (10 epochs).
Table 2: Noisy QCNN Parameters and Performance.
Parameters
Name Value
Number of Layers 10
Number of Features (PCA) 8
Number of Trainable Parameters 240
Number of Quantum Gates per Layer (without noise) 40
Number of Additional Noise Gates per Layer 32
Total Number of Quantum Gates per Layer 72
Optimizer Adam
Learning Rate 0.05
Indices
Name Value
Training Accuracy (5 Epochs) 71.25%
Test Accuracy (5 Epochs) 69.45%
Training Loss (5 Epochs) 0.97
Training Accuracy (10 Epochs) 69.28%
Test Accuracy (10 Epochs) 69.05%
Training Loss (10 Epochs) 0.44
AI4EIoT 2025 - Special Session on Artificial Intelligence for Emerging IoT Systems: Open Challenges and Novel Perspectives
514

cuits to real-world imperfections, with noticeable ac-
curacy degradation due to quantum noise.
While increasing the number of layers may im-
prove model expressiveness, it also exacerbates noise-
related issues. The results highlight the necessity
of quantum error correction and noise-aware circuit
design to make QCNNs viable for near-term quan-
tum devices. The findings suggest that while noise
presents a significant challenge, careful tuning of
learning parameters and error mitigation strategies
can help maintain competitive performance levels.
The runtime of the QCNN depends on several key
factors: the number of qubits, the number of layers,
the batch size, and the computational cost of opti-
mization. The total runtime is derived from three
main phases: preprocessing, quantum circuit execu-
tion, and optimization. The preprocessing steps in-
clude PCA, feature normalization, and train-test split-
ting. PCA dominates the complexity with an order of
O(Nd
2
), where N is the number of samples and d is
the original feature dimension.
The execution of the quantum circuit for each
batch depends on the number of qubits n, the num-
ber of layers L, and the number of quantum gates
per layer. Each batch requires evaluating all quantum
gates, leading to a complexity of O(BLn) per batch.
Since the parameter-shift rule for gradient computa-
tion requires two additional evaluations per parame-
ter, the total number of quantum circuit evaluations
per batch is O(6BL
2
n
2
).
The Adam optimizer updates parameters itera-
tively. Each update is proportional to the number of
parameters, O(3nL), and for T epochs, the total op-
timization complexity is O(T BLn). Combining this
with gradient evaluations, the dominant term remains
O(6T BL
2
n
2
).
Summing preprocessing, circuit execution, and
optimization, the total asymptotic runtime complex-
ity is in Eq. 16.
O(Nd
2
) + O(6T BL
2
n
2
) (16)
For a large dataset, quantum training dominates,
yielding O(T BL
2
n
2
).
In the noisy QCNN, depolarizing and phase damp-
ing noise are introduced through the de f ault.mixed
simulator, which requires simulating density matrices
instead of pure states. This increases the quantum
state dimension from 2
n
to 2
2n
, leading to an expo-
nential increase in computational cost, as in Eq. 17.
O(T BL
2
n
2
2
2n
). (17)
The exponential term reflects the additional cost
of simulating a noisy system that must track all pos-
sible mixed states. Table 3 summarises all these con-
siderations.
Table 3: Computational Complexity of QCNN Training.
Scenario Computational Complexity
Preprocessing (PCA, Normalization) O(Nd
2
)
Quantum Circuit Execution O(BLn)
Parameter-Shift Rule for Gradients O(6BL
2
n
2
)
Optimization (Adam Updates) O(T BLn)
Total Runtime (Noise-Free) O(T BL
2
n
2
)
Total Runtime (With Noise) O(T BL
2
n
2
2
2n
)
The model without noise scales polynomially with
the number of qubits and layers, the model with noise
scales exponentially with the number of qubits, sig-
nificantly limiting the ability to simulate large quan-
tum networks on classical computers.
6 CONCLUSION AND FUTURE
WORK
The comparative analysis of QCNNs under noise-free
and noisy conditions reveals key insights for facial
recognition tasks. In an ideal setting, the QCNNs
achieve a test accuracy of 75.62% after 10 epochs,
demonstrating strong generalization when quantum
decoherence and gate errors are negligible. However,
the introduction of noise reduces accuracy to 69.05%,
highlighting the detrimental effect of quantum noise.
The loss and accuracy curves indicate that the model
captures significant patterns, although discrepancies
between training and test performances suggest some
degree of overfitting, especially in the noise-free sce-
nario. With 40 gates per layer and 240 trainable
parameters, the architecture offers sufficient expres-
sivity yet remains constrained by the current limita-
tions of quantum hardware. Increasing the number of
epochs improves accuracy in both environments, al-
beit more modestly in the presence of noise, empha-
sizing the need for regularization techniques such as
quantum dropout and noise-aware training. All ex-
periments were conducted on the HPC server whose
specifications are provided in Table 4 4.
Table 4: Specifications of the HPC system used for QCNN
training.
Component Specification
HPC Server SuperServer 7089P-TR4T (Supermicro)
Hostname magicbox
CPU 8x Intel Xeon Platinum 8168 (2.7 GHz, 24 cores, 48 threads)
Cache Memory 33MB L3 per CPU
GPU 8x Nvidia P100 (16GB on-board RAM per GPU)
RAM 48x 32GB DDR4 2666 MHz (Total: 1536GB)
Storage (OS) 2x 480GB SSD (RAID 1)
Storage (Data) 4x 960GB SSD (RAID 6)
Operating System Linux CentOS 7.5
Quantum Convolutional Neural Networks for Image Classification: Perspectives and Challenges
515

6.1 Future Directions
This study opens several promising avenues to en-
hance the effectiveness and practical applicability of
QCNNs. Incorporating noise mitigation strategies, in-
cluding quantum error mitigation and correction tech-
niques, could help to bridge the performance gap be-
tween noise-free and noisy models. Optimizing the
quantum circuit architecture by reducing the number
of entangling CNOT gates or by employing more ro-
bust quantum feature maps may further improve re-
silience against hardware imperfections. Expanding
the current binary classification framework to multi-
class scenarios would provide a more comprehensive
assessment of scalability and generalization. Finally,
validating QCNNs on real quantum hardware is es-
sential for directly assessing noise effects and mak-
ing realistic comparisons with classical CNNs. In
summary, while this study confirms the feasibility of
QCNNs for image classification, further advances in
error correction, hardware performance, and training
strategies are critical to fully harnessing the potential
of quantum neural networks.
ACKNOWLEDGEMENTS
This work was funded bythe European Union
- NextGenerationEU under the project NRRP
(i)“National Centre for HPC, Big Data and Quan-
tum Computing (HPC)” CN00000013 (CUP
D43C22001240001) [MUR Decree n. 1031-
17/06/2022] - Cascade Call launched by SPOKE
10 POLIMI: “QML-NTED” project, (ii) “National
Quantum Science & Technology Institute (NQSTI)”
PE00000023 (CUP B53C22004180005) [MUR
Decree n. 341 15/03/2022] – Cascade Call launched
by SPOKE 8 CNR: “QUANTIC” project. EU-
FESR, PON Ricerca e Innovazione 2014-2020-DM
1062/2021. The experiments have been performed
by using the computing resources operated by the
Department of Mathematics and Physics of the
University of Campania “Luigi Vanvitelli”, Caserta,
Italy, within the VALERE Program.
REFERENCES
Chen, G., Chen, Q., Long, S., Zhu, W., Yuan, Z., and Wu,
Y. (2023). Quantum convolutional neural network for
image classification. Pattern Analysis and Applica-
tions, 26(2):655 – 667.
Easom-Mccaldin, P., Bouridane, A., Belatreche, A., Jiang,
R., and Al-Maadeed, S. (2024). Efficient quantum im-
age classification using single qubit encoding. IEEE
Transactions on Neural Networks and Learning Sys-
tems, 35(2):1472 – 1486.
Gong, L.-H., Pei, J.-J., Zhang, T.-F., and Zhou, N.-R.
(2024). Quantum convolutional neural network based
on variational quantum circuits. Optics Communica-
tions, 550.
Hassan, E., Hossain, M. S., Saber, A., Elmougy, S.,
Ghoneim, A., and Muhammad, G. (2024). A quan-
tum convolutional network and resnet (50)-based clas-
sification architecture for the MNIST medical dataset.
Biomedical Signal Processing and Control, 87.
Hilbert, M. and L
´
opez, P. (2011). The world’s technolog-
ical capacity to store, communicate, and compute in-
formation. Science, 332(6025):60–65.
Huang, G. B., Mattar, M., Berg, T., and Learned-Miller,
E. (2008). Labeled faces in the wild: A database
forstudying face recognition in unconstrained envi-
ronments. In Workshop on faces in’Real-Life’Images:
detection, alignment, and recognition.
Huang, S.-Y., An, W.-J., Zhang, D.-S., and Zhou, N.-R.
(2023). Image classification and adversarial robust-
ness analysis based on hybrid quantum–classical con-
volutional neural network. Optics Communications,
533.
Kharsa, R., Bouridane, A., and Amira, A. (2023). Advances
in quantum machine learning and deep learning for
image classification: A survey. Neurocomputing, 560.
Lazzarin, M., Galli, D. E., and Prati, E. (2022). Multi-
class quantum classifiers with tensor network circuits
for quantum phase recognition. Physics Letters A,
434:128056.
Lu, Y., Gao, Q., Lu, J., Ogorzalek, M., and Zheng, J. (2021).
A quantum convolutional neural network for image
classification. volume 2021-July, page 6329 – 6334.
Oh, S., Choi, J., Kim, J.-K., and Kim, J. (2021). Quantum
convolutional neural network for resource-efficient
image classification: A quantum random access mem-
ory (QRAM) approach. volume 2021-January, page
50 – 52.
Schuld, M. and Petruccione, F. (2021). Machine learning
with quantum computers, volume 676. Springer.
Sebastianelli, A., Zaidenberg, D. A., Spiller, D., Le Saux,
B., and Ullo, S. (2022). On circuit-based hybrid quan-
tum neural networks for remote sensing imagery clas-
sification. IEEE Journal of Selected Topics in Ap-
plied Earth Observations and Remote Sensing, 15:565
– 580.
Wall, M. L. and D’Aguanno, G. (2021). Tree-tensor-
network classifiers for machine learning: From quan-
tum inspired to quantum assisted. Physical Review A,
104(4):042408.
Zhang, Z., Mi, X., Yang, J., Wei, X., Liu, Y., Yan, J., Liu,
P., Gu, X., and Yu, T. (2023). Remote sensing im-
age scene classification in hybrid classical–quantum
transferring cnn with small samples. Sensors, 23(18).
AI4EIoT 2025 - Special Session on Artificial Intelligence for Emerging IoT Systems: Open Challenges and Novel Perspectives
516